Tight Fusion of a Monocular Camera, MEMS-IMU, and Single-Frequency Multi-GNSS RTK for Precise Navigation in GNSS-Challenged Environments
Abstract
:1. Introduction
2. Methods
2.1. Error State Model
2.2. Double-Differenced Measurement Model of the GPS/BeiDou/GLONASS System
2.3. Visual Measurement Model
2.4. Ambiguity Resolution with Inertial Aiding
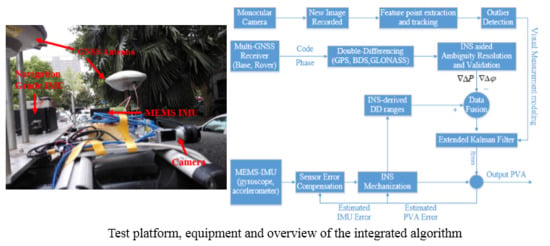
2.5. Overview of the Tightly Integrated Monocular Camera/INS/RTK System
3. Field Test Description and Data Processing Strategy
4. Results
4.1. Satellite Availability
4.2. Positioning Performance
4.3. Velocity Performance
4.4. Attitude Performance
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Martin, P.G.; Payton, O.D.; Fardoulis, J.S.; Richards, D.A.; Scott, T.B. The use of unmanned aerial systems for the mapping of legacy uranium mines. J. Environ. Radioact. 2015, 143, 135–140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Albéri, M.; Baldoncini, M.; Bottardi, C.; Chiarelli, E.; Fiorentini, G.; Raptis, K.G.C.; Realini, E.; Reguzzoni, M.; Rossi, L.; Sampietro, D.; et al. Accuracy of Flight Altitude Measured with Low-Cost GNSS, Radar and Barometer Sensors: Implications for Airborne Radiometric Surveys. Sensors 2017, 17, 1889. [Google Scholar] [CrossRef] [PubMed]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- He, H.; Li, J.; Yang, Y.; Xu, J.; Guo, H.; Wang, A. Performance assessment of single- and dual-frequency BeiDou/GPS single-epoch kinematic positioning. GPS Solut. 2014, 18, 393–403. [Google Scholar] [CrossRef]
- Carcanague, S.; Julien, O.; Vigneau, W.; Macabiau, C. Low-cost Single-frequency GPS/GLONASS RTK for Road Users. In Proceedings of the ION 2013 Pacific PNT Meeting, Honolulu, HI, USA, 23–25 April 2013; pp. 168–184. [Google Scholar]
- Teunissen, P.J.G.; Odolinski, R.; Odijk, D. Instantaneous BeiDou+GPS RTK positioning with high cut-off elevation angles. J. Geod. 2013, 88, 335–350. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G. Low-cost, high-precision, single-frequency GPS–BDS RTK positioning. GPS Solut. 2017, 21, 1315–1330. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G.; Odijk, D. Combined BDS, Galileo, QZSS and GPS single-frequency RTK. GPS Solut. 2014, 19, 151–163. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Niu, X.; Gao, Z. Tightly-Coupled Integration of Multi-GNSS Single-Frequency RTK and MEMS-IMU for Enhanced Positioning Performance. Sensors 2017, 17, 2462. [Google Scholar] [CrossRef] [PubMed]
- Grejner-Brzezinska, D.A.; Da, R.; Toth, C. GPS error modeling and OTF ambiguity resolution for high-accuracy GPS/INS integrated system. J. Geod. 1998, 72, 626–638. [Google Scholar] [CrossRef]
- Niu, X.; Zhang, Q.; Gong, L.; Liu, C.; Zhang, H.; Shi, C.; Wang, J.; Coleman, M. Development and evaluation of GNSS/INS data processing software for position and orientation systems. Surv. Rev. 2015, 47, 87–98. [Google Scholar] [CrossRef]
- Gao, Z.; Ge, M.; Shen, W.; Zhang, H.; Niu, X. Ionospheric and receiver DCB-constrained multi-GNSS single-frequency PPP integrated with MEMS inertial measurements. J. Geod. 2017, 91, 1351–1366. [Google Scholar] [CrossRef]
- Chiang, K.-W.; Duong, T.; Liao, J.-K. The Performance Analysis of a Real-Time Integrated INS/GPS Vehicle Navigation System with Abnormal GPS Measurement Elimination. Sensors 2013, 13, 10599. [Google Scholar] [CrossRef] [PubMed]
- Falco, G.; Gutiérrez, C.C.; Serna, E.P.; Zacchello, F.; Bories, S. Low-cost Real-time Tightly-Coupled GNSS/INS Navigation System Based on Carrier-phase Double- differences for UAV Applications. In Proceedings of the 27th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2014), Tampa, FL, USA, 8–12 September 2014; pp. 841–857. [Google Scholar]
- Eling, C.; Klingbeil, L.; Kuhlmann, H. Real-Time Single-Frequency GPS/MEMS-IMU Attitude Determination of Lightweight UAVs. Sensors 2015, 15, 26212. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Zhang, H.; Gao, Z.; Chen, Q.; Niu, X. High-accuracy positioning in urban environments using single-frequency multi-GNSS RTK/MEMS-IMU integration. Remote Sens. 2018, 10, 205. [Google Scholar] [CrossRef]
- Mourikis, A.I.; Roumeliotis, S.I. A multi-state constraint Kalman filter for vision-aided inertial navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3565–3572. [Google Scholar]
- Li, M.; Mourikis, A.I. High-precision, consistent EKF-based visual-inertial odometry. Int. J. Robot. Res. 2013, 32, 690–711. [Google Scholar] [CrossRef]
- Bloesch, M.; Omari, S.; Hutter, M.; Siegwart, R. Robust visual inertial odometry using a direct EKF-based approach. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 298–304. [Google Scholar]
- Wu, K.; Ahmed, A.; Georgiou, G.; Roumeliotis, S. A Square Root Inverse Filter for Efficient Vision-aided Inertial Navigation on Mobile Devices. In Proceedings of the Robotics: Science and Systems, Rome, Italy, 13–17 July 2015. [Google Scholar]
- Leutenegger, S.; Lynen, S.; Bosse, M.; Siegwart, R.; Furgale, P. Keyframe-based visual–inertial odometry using nonlinear optimization. Int. J. Robot. Res. 2015, 34, 314–334. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardos, J.D. Visual-Inertial Monocular SLAM with Map Reuse. IEEE Robot. Autom. Lett. 2016, 2, 796–803. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Grejner-Brzezinska, D.A.; Toth, C.K.; Moore, T.; Raquet, J.F.; Miller, M.M.; Kealy, A. Multisensor Navigation Systems: A Remedy for GNSS Vulnerabilities? Proc. IEEE 2016, 104, 1339–1353. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Sukkarieh, S. SLAM aided GPS/INS navigation in GPS denied and unknown environments. Positioning 2005, 4, 120–128. [Google Scholar] [CrossRef]
- Wang, J.; Garratt, M.; Lambert, A.; Wang, J.J.; Han, S.; Sinclair, D. Integration of GPS/INS/vision sensors to navigate unmanned aerial vehicles. In Proceedings of the International Society of Photogrammetry and Remote Sensing (ISPRS) Congress, Beijing, China, 3–11 July 2008; pp. 963–970. [Google Scholar]
- Chu, T.; Guo, N.; Backén, S.; Akos, D. Monocular camera/IMU/GNSS integration for ground vehicle navigation in challenging GNSS environments. Sensors 2012, 12, 3162–3185. [Google Scholar] [CrossRef] [PubMed]
- Oskiper, T.; Samarasekera, S.; Kumar, R. Multi-sensor navigation algorithm using monocular camera, IMU and GPS for large scale augmented reality. In Proceedings of the IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Atlanta, GA, USA, 5–8 November 2012; pp. 71–80. [Google Scholar]
- Vu, A.; Ramanandan, A.; Chen, A.; Farrell, J.A.; Barth, M. Real-Time Computer Vision/DGPS-Aided Inertial Navigation System for Lane-Level Vehicle Navigation. IEEE Trans. Intell. Transp. Syst. 2012, 13, 899–913. [Google Scholar] [CrossRef]
- Lynen, S.; Achtelik, M.W.; Weiss, S.; Chli, M.; Siegwart, R. A robust and modular multi-sensor fusion approach applied to mav navigation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3923–3929. [Google Scholar]
- Shepard, D.P.; Humphreys, T.E. High-precision globally-referenced position and attitude via a fusion of visual SLAM, carrier-phase-based GPS, and inertial measurements. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014; pp. 1309–1328. [Google Scholar]
- Mascaro, R.; Teixeira, L.; Hinzmann, T.; Siegwart, R.; Chli, M. GOMSF: Graph-Optimization based Multi-Sensor Fusion for robust UAV pose estimation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2018), Brisbane, Australia, 21–25 May 2018; pp. 1421–1428. [Google Scholar]
- Jekeli, C. Inertial navigation systems with geodetic applications; Walter de Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Park, M. Error Analysis and Stochastic Modeling of MEMS Based Inertial Sensors for Land Vehicle Navigation Applications. Ph.D. Thesis, University of Calgary, Calgary, AL, Canada, 2004. [Google Scholar]
- Wanninger, L. Carrier-phase inter-frequency biases of GLONASS receivers. J. Geod. 2012, 86, 139–148. [Google Scholar] [CrossRef]
- Tian, Y.; Ge, M.; Neitzel, F. Particle filter-based estimation of inter-frequency phase bias for real-time GLONASS integer ambiguity resolution. J. Geod. 2015, 89, 1145–1158. [Google Scholar] [CrossRef]
- Petovello, M. GLONASS inter-frequency biases and ambiguity resolution. Inside GNSS 2009, 4, 24–28. [Google Scholar]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Ji, S.; Chen, W.; Ding, X.; Chen, Y.; Zhao, C.; Hu, C. Ambiguity validation with combined ratio test and ellipsoidal integer aperture estimator. J. Geod. 2010, 84, 597–604. [Google Scholar] [CrossRef]
- Verhagen, S. On the Reliability of Integer Ambiguity Resolution. Navigation 2005, 52, 99–110. [Google Scholar] [CrossRef]
- Bouguet, J.-Y. Camera Calibration Toolbox for MATLAB. Available online: http://www.vision.caltech.edu/bouguetj/calib_doc/index.html (accessed on 16 October 2018).
- Furgale, P.; Rehder, J.; Siegwart, R. Unified temporal and spatial calibration for multi-sensor systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1280–1286. [Google Scholar]
- Rosten, E.; Porter, R.; Drummond, T. Faster and Better: A Machine Learning Approach to Corner Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 105–119. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Tomasi, C. Good Features to Track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994; pp. 593–600. [Google Scholar]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the Intenational Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; pp. 121–130. [Google Scholar]
- Gao, Z.; Ge, M.; Shen, W.; You, L.; Chen, Q.; Zhang, H.; Niu, X. Evaluation on the impact of IMU grades on BDS+GPS PPP/INS tightly coupled integration. Adv. Space Res. 2017, 60, 1283–1299. [Google Scholar] [CrossRef]
- Kelly, J.; Sukhatme, G.S. Visual-inertial sensor fusion: Localization, mapping and sensor-to-sensor self-calibration. Int. J. Robot. Res. 2011, 30, 56–79. [Google Scholar] [CrossRef]
- Sinpyo, H.; Man Hyung, L.; Ho-Hwan, C.; Sun-Hong, K.; Speyer, J.L. Observability of error States in GPS/INS integration. IEEE Trans. Veh. Technol. 2005, 54, 731–743. [Google Scholar] [CrossRef]





















| IMU Sensors | Bias | Random Walk | ||
|---|---|---|---|---|
| Acce. (mGal) | ||||
| Navigation grade | 0.027 | 15 | 0.003 | 0.03 |
| MEMS grade | 10.0 | 1500 | 0.33 | 0.18 |
| RTK/INS | RTK/INS/Vision | Improvement (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RMS(m) | North | East | Down | North | East | Down | North | East | Down |
| GPS | 1.182 | 1.346 | 2.717 | 0.474 | 0.390 | 0.308 | 59.9 | 71.0 | 88.7 |
| G + C | 1.206 | 1.097 | 2.016 | 0.177 | 0.232 | 0.076 | 85.3 | 78.9 | 96.2 |
| G + C + R | 1.092 | 0.985 | 1.556 | 0.152 | 0.219 | 0.065 | 86.1 | 77.8 | 95.8 |
| RTK/INS | RTK/INS/Vision | Improvement (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RMS (m/s) | North | East | Down | North | East | Down | North | East | Down |
| GPS | 0.092 | 0.119 | 0.075 | 0.038 | 0.050 | 0.025 | 58.7 | 58.0 | 66.7 |
| G+C | 0.091 | 0.103 | 0.075 | 0.028 | 0.048 | 0.025 | 69.2 | 53.4 | 66.7 |
| G+C+R | 0.082 | 0.094 | 0.055 | 0.028 | 0.046 | 0.025 | 65.9 | 51.1 | 54.5 |
| RTK/INS | RTK/INS/Vision | Improvement (%) | |||||
|---|---|---|---|---|---|---|---|
| RMS (deg) | Roll | Pitch | Yaw | Roll | Pitch | Yaw | Yaw |
| GPS | 0.070 | 0.063 | 0.500 | 0.066 | 0.046 | 0.134 | 73.2 |
| G + C | 0.066 | 0.058 | 0.214 | 0.065 | 0.045 | 0.099 | 53.7 |
| G + C + R | 0.068 | 0.052 | 0.198 | 0.066 | 0.044 | 0.092 | 53.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Zhang, H.; Gao, Z.; Niu, X.; El-sheimy, N. Tight Fusion of a Monocular Camera, MEMS-IMU, and Single-Frequency Multi-GNSS RTK for Precise Navigation in GNSS-Challenged Environments. Remote Sens. 2019, 11, 610. https://doi.org/10.3390/rs11060610
Li T, Zhang H, Gao Z, Niu X, El-sheimy N. Tight Fusion of a Monocular Camera, MEMS-IMU, and Single-Frequency Multi-GNSS RTK for Precise Navigation in GNSS-Challenged Environments. Remote Sensing. 2019; 11(6):610. https://doi.org/10.3390/rs11060610
Chicago/Turabian StyleLi, Tuan, Hongping Zhang, Zhouzheng Gao, Xiaoji Niu, and Naser El-sheimy. 2019. "Tight Fusion of a Monocular Camera, MEMS-IMU, and Single-Frequency Multi-GNSS RTK for Precise Navigation in GNSS-Challenged Environments" Remote Sensing 11, no. 6: 610. https://doi.org/10.3390/rs11060610
APA StyleLi, T., Zhang, H., Gao, Z., Niu, X., & El-sheimy, N. (2019). Tight Fusion of a Monocular Camera, MEMS-IMU, and Single-Frequency Multi-GNSS RTK for Precise Navigation in GNSS-Challenged Environments. Remote Sensing, 11(6), 610. https://doi.org/10.3390/rs11060610