Evaluating GIS-Based Multiple Statistical Models and Data Mining for Earthquake and Rainfall-Induced Landslide Susceptibility Using the LiDAR DEM
Abstract
:1. Introduction
2. Overview of the Study Area
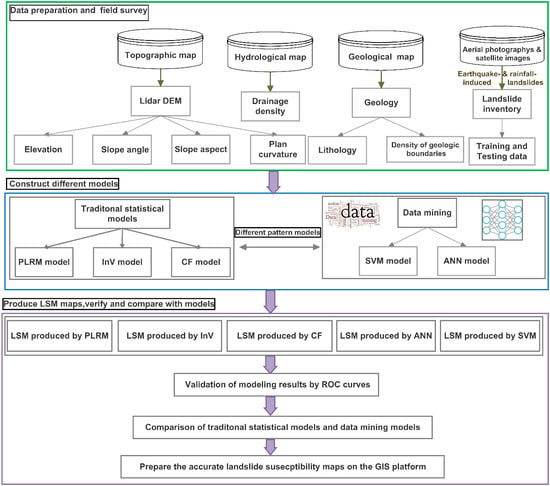
3. Materials and Methods
3.1. Landslide Inventory and Data Collection
3.2. Common Factors Controlling Earthquake- and Rainfall-Induced Landslides
3.2.1. Elevation
3.2.2. Slope Angle
3.2.3. Slope Aspect
3.2.4. Plan Curvature
3.2.5. Drainage Density
3.2.6. Density of Geologic Boundaries
3.2.7. Lithology
3.3. Methods
3.3.1. Probabilistic Likelihood-Frequency Ratio
3.3.2. Information Value Method
3.3.3. Certainty Factors
3.3.4. Artificial Neural Network
3.3.5. Support Vector Machine
3.4. Accuracy Assessment of the Models
4. Results
4.1. Modeling Result with the Probabilistic Likelihood-Frequency Ratio
4.2. Modeling Result with the Information Value (InV)
4.3. Modeling Result with the Certainty Factors
4.4. Modeling Result with the ANN
4.5. Modeling result with the SVM
4.6. Model Validation
5. Discussion
6. Conclusions
- The high quality of the susceptibility map can be obtained with the use of data mining (SVM and ANN) for landslides triggered by both earthquake and rainfall.
- Although traditional statistical techniques, PLFR, InV and CF, provide low prediction performance of landslide models; however, they are still useful, that is, capacities to reveal high probabilities of the landslide of causative factors’ classes.
- LiDAR-derived data are an important source for deriving high-quality susceptibility map.
- Landslide susceptibility maps developed in this study are of great importance for sustainable urban development and thus the local government. The information derived from the constructed map may be helpful in preliminary decision-making and policy planning. For the hazard zonation, they could opt for some low susceptibility index as a relatively safe area to design the appropriate countermeasures. Furthermore, more relative data are needed to acquire for wide application in more regional areas.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Marano, K.D.; Wald, D.J.; Allen, T.I. Global earthquake casualties due to secondary effects: A quantitative analysis for improving rapid loss analyses. Nat. Hazards 2010, 319–328. [Google Scholar] [CrossRef]
- Times, J. 80% of Victims in Atsuma, hardest-Hit by Hokkaido Quake, Died of Suffocation. Available online: https://www.japantimes.co.jp/news/2018/09/11/natio (accessed on 10 December 2018).
- Turner, A.K.; Schuster, R. Landslides: Investigation and Mitigation; Transportation Research Board: Washington, DC, USA, 1996. [Google Scholar]
- Camilo, D.C.; Lombardo, L.; Mai, P.M.; Dou, J.; Huser, R. Handling high predictor dimensionality in slope-unit-based landslide susceptibility models through LASSO-penalized Generalized Linear Model. Environ. Model. Softw. 2017, 97, 145–156. [Google Scholar] [CrossRef]
- Dou, J.; Li, X.; Yunus, A.P.; Paudel, U. Automatic detection of sinkhole collapses at finer resolutions using a multi-component remote sensing approach. Nat. Hazards 2015, 1021–1044. [Google Scholar] [CrossRef]
- Dou, J.; Yamagishi, H.; Xu, Y.; Zhu, Z.; Yunus, A.P. Characteristics of the Torrential Rainfall-Induced Shallow Landslides by Typhoon Bilis, in July 2006, Using Remote Sensing and GIS. In GIS Landslide; Yamagishi, H., Bhandary, N.P., Eds.; Springer: Tokyo, Japan, 2017; pp. 221–230. ISBN 978-4-431-54391-6. [Google Scholar]
- Dou, J.; Oguchi, T.; Hayakawa, Y.S.; Uchiyama, S.; Saito, H.; Paudel, U. GIS-based landslide susceptibility mapping using a certainty factor model and its validation in the Chuetsu area, central Japan. In Landslide Science for a Safer Geoenvironment: Volume 2: Methods of Landslide Studies; Springer: Cham, Switzerland, 2014; pp. 419–424. ISBN 9783319050508. [Google Scholar]
- Chang, K.T.; Dou, J.; Chang, Y.; Kuo, C.P.; Xu, K.M.; Liu, J.K. Spatial resolution effects of digital terrain models on landslide susceptibility analysis. Remote Sens. Spat. Inf. Sci. 2016, XLI-B8, 33–36. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, H.; Pang, B.; Dou, J.; Peng, D. Comparison of Conventional Deterministic and Entropy-Based Methods for Predicting Sediment Concentration in Debris Flow. Water 2019, 11, 439. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide Susceptibility Assessment in Vietnam Using Support Vector Machines, Decision Tree, and Naïve Bayes Models. Math. Probl. Eng. 2012, 2012, 1–26. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Tien Bui, D.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Kanungo, D.P.; Sarkar, S.; Sharma, S. Combining neural network with fuzzy, certainty factor and likelihood ratio concepts for spatial prediction of landslides. Nat. Hazards 2011, 59, 1491–1512. [Google Scholar] [CrossRef]
- Thai Pham, B.; Prakash, I.; Dou, J.; Singh, S.K.; Trinh, P.T.; Trung Tran, H.; Minh Le, T.; Tran, V.P.; Kim Khoi, D.; Shirzadi, A.; et al. A Novel Hybrid Approach of Landslide Susceptibility Modeling Using Rotation Forest Ensemble and Different Base Classifiers. Geocarto Int. 2018, 1–38. [Google Scholar] [CrossRef]
- Aleotti, P.; Chowdhury, R. Landslide hazard assessment: Summary review and new perspectives. Bull. Eng. Geol. Environ. 1999, 58, 21–44. [Google Scholar] [CrossRef]
- Dadson, S.J.; Hovius, N.; Chen, H.; Dade, W.B.; Lin, J.C.; Hsu, M.L.; Lin, C.W.; Horng, M.J.; Chen, T.C.; Milliman, J.; et al. Earthquake-triggered increase in sediment delivery from an active mountain belt. Geology 2004, 32, 733–736. [Google Scholar] [CrossRef]
- Schlögel, R.; Marchesini, I.; Alvioli, M.; Reichenbach, P.; Rossi, M.; Malet, J.P. Optimizing landslide susceptibility zonation: Effects of DEM spatial resolution and slope unit delineation on logistic regression models. Geomorphology 2018, 301, 10–20. [Google Scholar] [CrossRef]
- Claessens, L.; Heuvelink, G.; Schoorl, J.M.; Veldkamp, A. DEM resolution effects on shallow landslide hazard and soil redistribution modelling. Earth Surf. Processes Landf. 2005, 30, 461–477. [Google Scholar] [CrossRef]
- Zhang, W.; Montgomery, D.R. Digital elevation model grid size, landscape representation, and hydrologic simulations. Water Resour. Res. 1994, 30, 1019–1028. [Google Scholar] [CrossRef]
- Dietrich, W.; Montgomery, D. Scale Dependence and Scale Invariance in Hydrolog; Sposito, G., Ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Castellanos Abella, E.A.; Van Westen, C.J. Qualitative landslide susceptibility assessment by multicriteria analysis: A case study from San Antonio del Sur, Guantánamo, Cuba. Geomorphology 2008, 94, 453–466. [Google Scholar] [CrossRef]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Optimization of landslide conditioning factors using very high-resolution airborne laser scanning (LiDAR) data at catchment scale. Remote Sens. Environ. 2014, 152, 150–165. [Google Scholar] [CrossRef]
- Dou, J.; Paudel, U.; Oguchi, T.; Uchiyama, S.; Hayakawa, Y.S. Shallow and Deep-Seated Landslide Differentiation Using Support Vector Machines: A Case Study of the Chuetsu Area, Japan. Terr. Atmos. Ocean. Sci. 2015, 26, 227. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Choffet, M.; Derron, M.-H.; Horton, P.; Loye, A.; Longchamp, C.; Mazotti, B.; Michoud, C.; Pedrazzini, A. Preliminary Slope Mass Movement Susceptibility Mapping Using DEM and LiDAR DEM. In Terrigenous Mass Movements; Springer Berlin Heidelberg: Berlin, Heidelberg, 2012; ISBN 9783642254956. [Google Scholar]
- Ghuffar, S.; Szekely, B.; Roncat, A.; Pfeifer, N. Landslide Displacement Monitoring Using 3D Range Flow on Airborne and Terrestrial LiDAR Data. Remote Sens. 2013, 5, 2720–2745. [Google Scholar] [CrossRef]
- Dou, J.; Qian, J.; Zhang, H.; Chen, S.; Zheng, X.; Zhu, J.; Xie, Z.; Zou, Y. Landslides detection: A case study in Conghua city of Pearl River delta. In Proceedings of the Second International Conference on Earth Observation for Global Changes, Chengdu, China, 25–29 May 2009. [Google Scholar] [CrossRef]
- Dou, J.; Chang, K.T.; Chen, S.; Yunus, A.P.; Liu, J.K.; Xia, H.; Zhu, Z. Automatic Case-Based Reasoning Approach for Landslide Detection: Integration of Object-Oriented Image Analysis and a Genetic Algorithm. Remote Sens. 2015, 7, 4318–4342. [Google Scholar] [CrossRef]
- Bijukchhen, S.M.; Kayastha, P.; Dhital, M.R. A comparative evaluation of heuristic and bivariate statistical modelling for landslide susceptibility mappings in Ghurmi-Dhad Khola, east Nepal. Arab. J. Geosci. 2013, 6, 2727–2743. [Google Scholar] [CrossRef]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- De Vita, P.; Napolitano, E.; Godt, J.W.; Baum, R.L. Deterministic estimation of hydrological thresholds for shallow landslide initiation and slope stability models: Case study from the Somma-Vesuvius area of southern Italy. Landslides 2013, 10, 713–728. [Google Scholar] [CrossRef]
- Shahabi, H.; Ahmad, B.B.; Khezri, S. Evaluation and comparison of bivariate and multivariate statistical methods for landslide susceptibility mapping (case study: Zab basin). Arab. J. Geosci. 2013, 6, 3885–3907. [Google Scholar] [CrossRef]
- Dou, J.; Bui, D.T.; Yunus, A.P.; Jia, K.; Song, X.; Revhaug, I.; Xia, H.; Zhu, Z. Optimization of causative factors for landslide susceptibility evaluation using remote sensing and GIS data in parts of Niigata, Japan. PLoS ONE 2015, 10, e0133262. [Google Scholar] [CrossRef] [PubMed]
- Binaghi, E.; Luzi, L.; Madella, P.; Pergalani, F.; Rampini, A. Slope Instability Zonation: A Comparison Between Certainty Factor and Fuzzy Dempster–Shafer Approaches. Nat. Hazards 1998, 17, 77–97. [Google Scholar] [CrossRef]
- Dou, J.; Yamagishi, H.; Pourghasemi, H.R.; Yunus, A.P.; Song, X.; Xu, Y.; Zhu, Z. An integrated artificial neural network model for the landslide susceptibility assessment of Osado Island, Japan. Nat. Hazards 2015, 78, 1749–1776. [Google Scholar] [CrossRef]
- Collins, B.D.; Kayen, R.; Tanaka, Y. Spatial distribution of landslides triggered from the 2007 Niigata Chuetsu–Oki Japan Earthquake. Eng. Geol. 2012, 127, 14–26. [Google Scholar] [CrossRef]
- Has, B.; Nozaki, T. Role of geological structure in the occurrence of earthquake-induced landslides, the case of the 2007 Mid-Niigata Offshore Earthquake, Japan. Eng. Geol. 2014, 182, 25–36. [Google Scholar] [CrossRef]
- Yamagishi, H.; Marui, H.; Ayalew, L.; Sekiguchi, T.; Horimatsu, T.; Hatamoto, M. Estimation of the sequence and size of the Tozawagawa landslide, Niigata, Japan, using aerial photographs. Landslides 2004, 1, 299–303. [Google Scholar] [CrossRef]
- Takeuchi, K.; Yanagisawa, Y. 1:50,000 Digital Geological Map of the Uonuma Region, Niigata Prefecture (Ver. 1); Geological Survey of Japan: Tsukuba, Japan, 2004; Volume V20B-2. [Google Scholar]
- Varnes, D.J. Slope movement types and processes, in Schuster, R.L., and Krizek, R.J., eds., Landslides—Analysis and control. Natl. Acad. Sci. Transp. Res. Board Spec. Rep. 1978, 176, 11–33. [Google Scholar]
- Aksoy, B.; Ercanoglu, M. Landslide identification and classification by object-based image analysis and fuzzy logic: An example from the Azdavay region (Kastamonu, Turkey). Comput. Geosci. 2012, 38, 87–98. [Google Scholar] [CrossRef]
- Xu, C.; Ma, S.; Tan, Z.; Xie, C.; Toda, S.; Huang, X. Landslides triggered by the 2016 Mj 7. 3 Kumamoto, Japan, earthquake. Landslide 2018, 26, 551–564. [Google Scholar] [CrossRef]
- Chang, K.-T.; Chiang, S.-H.; Hsu, M.-L. Modeling typhoon- and earthquake-induced landslides in a mountainous watershed using logistic regression. Geomorphology 2007, 89, 335–347. [Google Scholar] [CrossRef]
- García-Rodríguez, M.J.; Malpica, J.A. Assessment of earthquake-triggered landslide susceptibility in El Salvador based on an artificial neural network model. Nat. Hazards Earth Syst. Sci. 2010, 10, 1307–1315. [Google Scholar] [CrossRef]
- Bhandary, N.P.; Dahal, R.K.; Timilsina, M.; Yatabe, R. Rainfall event-based landslide susceptibility zonation mapping. Natural Hazards 2013, 69, 365–388. [Google Scholar] [CrossRef]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Tanyaş, H.; Allstadt, K.E.; van Westen, C.J. An updated method for estimating landslide-event magnitude. Earth Surf. Processes Landf. 2018, 43, 1836–1847. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pradhan, B.; Jebur, M.N.; El-Harbi, H.M. Landslide susceptibility mapping using ensemble bivariate and multivariate statistical models in Fayfa area, Saudi Arabia. Environ. Earth Sci. 2015, 73, 3745–3761. [Google Scholar] [CrossRef]
- Peckham, S.D. Profile, plan and streamline curvature: A simple derivation and applications. In Proceedings of the Geomorphometry, Redlands, CA,USA, 7–11 September 2011; 2011; Volume 4, pp. 27–30. [Google Scholar]
- Ohlmacher, G.C. Plan curvature and landslide probability in regions dominated by earth flows and earth slides. Eng. Geol. 2007, 91, 117–134. [Google Scholar] [CrossRef]
- Lin, W.T.; Chou, W.C.; Lin, C.Y.; Huang, P.H.; Tsai, J.S. Automated suitable drainage network extraction from digital elevation models in Taiwan’s upstream watersheds. Hydrol. Processes 2006, 20, 289–306. [Google Scholar] [CrossRef]
- Hayakawa, Y.S.; Oguchi, T. GIS analysis of fluvial knickzone distribution in Japanese mountain watersheds. Geomorphology 2009. [Google Scholar] [CrossRef]
- Oguchi, T. Drainage density and relative relief in humid steep mountains with frequent slope failure. Earth Surf. Processes Landf. 1997, 22, 107–120. [Google Scholar] [CrossRef]
- Kawabata, D.; Bandibas, J. Landslide susceptibility mapping using geological data, a DEM from ASTER images and an Artificial Neural Network (ANN). Geomorphology 2009, 113, 97–109. [Google Scholar] [CrossRef]
- Yalcin, A.; Reis, S.; Aydinoglu, A.C.; Yomralioglu, T. A GIS-based comparative study of frequency ratio, analytical hierarchy process, bivariate statistics and logistics regression methods for landslide susceptibility mapping in Trabzon, NE Turkey. Catena 2011, 85, 274–287. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide susceptibility assessment and factor effect analysis: Backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling. Environ. Model. Softw. 2010, 25, 747–759. [Google Scholar] [CrossRef]
- Van Westen, C.J.; Asch, T.W.J.; Soeters, R.; Westen, C.J. Landslide hazard and risk zonation—Why is it still so difficult? Bull. Eng. Geol. Environ. 2005, 65, 167–184. [Google Scholar] [CrossRef]
- Chung, C.-J.; Fabbri, A.G. The representation of geoscience information for data integration. Nonrenew. Resour. 1993, 2, 122–139. [Google Scholar] [CrossRef]
- Ostad-Ali-Askari, K.; Shayannejad, M.; Ghorbanizadeh-Kharazi, H. Artificial neural network for modeling nitrate pollution of groundwater in marginal area of Zayandeh-rood River, Isfahan, Iran. KSCE J. Civ. Eng. 2017. [Google Scholar] [CrossRef]
- Khosravi, A.; Koury, R.N.N.; Machado, L.; Pabon, J.J.G. Prediction of wind speed and wind direction using artificial neural network, support vector regression and adaptive neuro-fuzzy inference system. Sustain. Energy Technol. Assess. 2018. [Google Scholar] [CrossRef]
- Dou, J.; Yamagishi, H.; Zhu, Z.; Yunus, A.P.; Chen, C.W. A Comparative Study of the Binary Logistic Regression (BLR) and Artificial Neural Network (ANN) Models for GIS-Based Spatial Predicting Landslides at a Regional Scale. In Landslide Dynamics: ISDR-ICL Landslide Interactive Teaching Tools: Volume 1: Fundamentals, Mapping and Monitoring; Springer: Cham, Switzerland, 2018; pp. 139–151. ISBN 978-3-319-53486-2. [Google Scholar]
- Pham, B.T.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 2017. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory (Adaptive and Learning Systems for Signal Processing, Communications and Control Series); Wiley-Interscience: Hoboken, NJ, USA, 1998; ISBN 0471030031. [Google Scholar]
- Su, C.; Wang, L.; Wang, X.; Huang, Z.; Zhang, X. Mapping of rainfall-induced landslide susceptibility in Wencheng, China, using support vector machine. Nat. Hazards 2015, 76, 1759–1779. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, H.; Peng, D.; Dou, J. Modelling the Hindered Settling Velocity of a Falling Particle in a Particle-Fluid Mixture by the Tsallis Entropy Theory. Entropy 2019, 21, 55. [Google Scholar] [CrossRef]
- Irigaray, C.; Fernández, T.; El Hamdouni, R.; Chacón, J. Evaluation and validation of landslide-susceptibility maps obtained by a GIS matrix method: Examples from the Betic Cordillera (southern Spain). Nat. Hazards 2006, 41, 61–79. [Google Scholar] [CrossRef]
- Swets, J.A. Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef]
- Yesilnacar, E.; Topal, T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Yilmaz, I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: A case study from Kat landslides (Tokat—Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Li, Y.; Chen, G.; Tang, C.; Zhou, G.; Zheng, L. Rainfall and earthquake-induced landslide susceptibility assessment using GIS and Artificial Neural Network. Nat. Hazards Earth Syst. Sci. 2012, 12, 2719–2729. [Google Scholar] [CrossRef]
- Iwahashi, J.; Kamiya, I.; Yamagishi, H. High-resolution DEMs in the study of rainfall- and earthquake-induced landslides: Use of a variable window size method in digital terrain analysis. Geomorphology 2012, 153, 29–38. [Google Scholar] [CrossRef]
- Saito, H.; Uchiyama, S.; Hayakawa, Y.S.; Obanawa, H. Landslides triggered by an earthquake and heavy rainfalls at Aso volcano, Japan, detected by UAS and SfM-MVS photogrammetry. Progr. Earth Planet. Sci. 2018. [Google Scholar] [CrossRef]
- Oguchi, T. Factors affecting the magnitude of post-glacial hillslope incision in Japanese mountains. Catena 1996, 26, 171–186. [Google Scholar] [CrossRef]
- Merghadi, A.; Abderrahmane, B.; Tien Bui, D. Landslide Susceptibility Assessment at Mila Basin (Algeria): A Comparative Assessment of Prediction Capability of Advanced Machine Learning Methods. ISPRS Int. J. Geo-Inf. 2018, 7, 268. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using GIS-based machine learning techniques for Chongren County, Jiangxi Province, China. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]
- Pradhan, B.; Sameen, M.I. Manifestation of SVM-Based Rectified Linear Unit (ReLU) Kernel Function in Landslide Modelling. In Space Science and Communication for Sustainability; Springer Singapore: Singapore, 2018; pp. 185–195. [Google Scholar]











| Thematic Layer | Causative Factors | Data Type | Scale or Resolution | Classes | Producer | Description |
|---|---|---|---|---|---|---|
| Landslide inventory map | Landslide | Polygon | 1:50,000 | Continuous | NIED and interpretations | Landslide occurrence |
| Geological map | Lithology | Polygon | 1:50,000 | Non-continuous | Geological Survey of Japan | Type of lithology |
| Density of geological boundary | Line | Continuous | Density of geologic unit | |||
| Topographic map | Elevation | Continuous | Geographical Survey Institute | Elevation-m | ||
| Slope angle | Continuous | Slope degree | ||||
| Slope aspect | ARC/INFO | 2 × 2 m | Continuous | Direction | ||
| Plan curvature | Grid | Continuous | Concave or convex | |||
| Hydrological Map | Drainage density | Continuous | Density |
| Geologic Age | Lithology | Geologic Unit |
|---|---|---|
| Holocene | Gravel, sand and silt | a |
| Gravel and sand | al | |
| Debris, gravel and sand | d | |
| Gravel and sand | f | |
| Gravel, sand and silt | tk | |
| Late Pleistocene | Debris and colluvial soil | c |
| Gravel, sand and silt | tl2 | |
| Gravel, sand and silt | tl1 | |
| Middle Pleistocene | Gravel, sand and silt | tm2 |
| Gravel, sand and silt | tm1 | |
| Gravel, sand and silt | th2 | |
| Gravel, sand and silt | th1 | |
| Gravel, sand and mud | Oy | |
| Late Pliocene–Early | Marine silt and sand | Ue |
| Pleistocene | Gravel, sand and silt | Ud |
| Gravel, sand and silt | Uc | |
| Gravel and sand | tk2 | |
| Late Pliocene | Sandstone | W |
| Sandy siltstone and alternation of sandstone and siltstone | S | |
| Early Pliocene– | Andesite, dacite lava and pyroclastic rock | Ka |
| Late Pliocene | Tuffaceous sandstone and Andesitic pyroclastic rock | Sy |
| Massive mudstone | Um | |
| Andesitic pyroclastic rock | Uv | |
| Sandstone | Ks | |
| Mudstone interbedded with sandstone | Ku | |
| Late Miocene– | Sandstone interbedded with mudstone | Kl |
| Andesitic pyroclastic rock | Av | |
| Early Pliocene | Sandstone and alternation of sandstone and mudstone | As |
| Massive mudstone | Am | |
| Late Miocene | Dacite, andesite lava and volcanic breccia | Tv |
| Massive mudstone | Ts | |
| Middle Miocene– | Dacite lava and pyroclastic rock | Nd |
| Andesitic pyroclastic rock | Sv | |
| Late Miocene | Hard shale and alternation of sandstone and shale | Sm |
| (Water) | (w) |
| Variables | Variables Setting |
|---|---|
| Root mean square error (RMSE) | 0.001 |
| Initial weights | 0.1–0.25 |
| Learning rate | 0.01 |
| Number of epochs | 3000 iterations |
| Momentum parameters | 0.9 |
| Activation (transfer) function for layers | Transig for hidden layer, purelin for the output layer |
| Total Number | Event | Sum | ||
|---|---|---|---|---|
| Condition Positive | Condition Negative | |||
| Test result | Positive | True positive (TP) | False positive (FR) | TP + FR |
| Negative | False negative (FN) | True negative (TN) | FN + TN | |
| Sum | TP + FN | FR + TN | TP + FR+ FN+ TN | |
| Rank | Range | Description |
|---|---|---|
| 1 | 0.9–1 | Excellent |
| 2 | 0.8–0.9 | Good |
| 3 | 0.7–0.8 | Acceptable |
| 4 | 0.6–0.7 | Poor |
| 5 | 0.5–0.6 | Failed |
| Factors | Class | Percentage of Domain (%) | Percentage of Landslides (%) | CF | PLFR | Wi (InV) |
|---|---|---|---|---|---|---|
| Elevation (m) | 0–73 | 18.14 | 1.01 | −0.96 | 0.06 | −0.2 |
| 73–131 | 17.67 | 6.86 | −0.68 | 0.39 | 1.41 | |
| 131–190 | 15.36 | 19.96 | 0.31 | 1.3 | 2.71 | |
| 190–246 | 13.49 | 23.37 | 0.57 | 1.73 | 2.98 | |
| 246–301 | 11.65 | 19.35 | 0.54 | 1.66 | 2.94 | |
| 301–357 | 8.73 | 15.23 | 0.58 | 1.74 | 2.88 | |
| 357–413 | 6.57 | 9.32 | 0.4 | 1.42 | 2.66 | |
| 413–477 | 4.89 | 4.23 | −0.17 | 0.87 | 1.74 | |
| 477–561 | 2.67 | 0.51 | −0.85 | 0.19 | 0.5 | |
| 561–735 | 0.84 | 0.15 | −0.86 | 0.18 | −0.42 | |
| Slope angle (°) | 0–10 | 39.37 | 4.72 | −0.91 | 0.12 | −1.25 |
| 43390 | 12.91 | 9.74 | −0.3 | 0.75 | 0.01 | |
| 17–27 | 19.62 | 22.17 | 0.17 | 1.13 | 0.36 | |
| 27–39 | 21.75 | 39.42 | 0.61 | 1.81 | 0.52 | |
| 39–55 | 6.2 | 23.82 | 1 | 3.84 | 0.57 | |
| 55–70 | 0.16 | 0.14 | −0.18 | 0.85 | 0.42 | |
| Slope aspect | Flat | 17.97 | 7.72 | −0.88 | 0.85 | 1.81 |
| Northeast | 9.5 | 6.34 | −0.4 | 0.67 | 2.21 | |
| East | 10.06 | 11.12 | 0.13 | 1.11 | 2.48 | |
| Southeast | 9.7 | 15.01 | 0.48 | 1.55 | 2.66 | |
| South | 9.19 | 15.76 | 0.57 | 1.71 | 2.76 | |
| Southwest | 10.34 | 15.73 | 0.47 | 1.52 | 2.66 | |
| West | 11.99 | 14.15 | 0.21 | 1.18 | 2.54 | |
| Northwest | 11.78 | 8.98 | −0.3 | 0.76 | 2.25 | |
| North | 9.48 | 5.19 | −0.53 | 0.55 | 2.08 | |
| Plan curvature | Concave | 57.46 | 49.49 | −0.18 | 0.89 | 2.27 |
| Convex | 42.54 | 50.51 | 0.21 | 1.15 | 2.53 | |
| Drainage density | 0–2 | 27.24 | 21.25 | −0.31 | 0.78 | 1.97 |
| 2–4 | 27.24 | 28.66 | 0.02 | 1.05 | 2.35 | |
| 4–6 | 24.57 | 29.89 | 0.2 | 1.22 | 2.63 | |
| 6–9 | 15.45 | 17.28 | 0.1 | 1.12 | 2.55 | |
| 9–20 | 5.5 | 2.92 | −0.56 | 0.53 | 1.77 | |
| Density of geological boundary | 0–2 | 30.82 | 15.59 | −0.58 | 0.51 | 1.6 |
| 2–5 | 20.67 | 21.73 | 0.03 | 1.05 | 2.34 | |
| 5–7 | 20.79 | 25.26 | 0.21 | 1.22 | 2.52 | |
| 7–10 | 15.13 | 18.19 | 0.19 | 1.2 | 2.51 | |
| 10–15 | 9.47 | 14.13 | 0.42 | 1.49 | 2.82 | |
| 15–27 | 3.13 | 5.09 | 0.5 | 1.63 | 3.31 | |
| Lithology | w | 3.22 | 1.05 | −0.68 | 0.33 | 1.8 |
| Av | 2.07 | 2.34 | 0.34 | 1.13 | 2.28 | |
| Um | 6.63 | 13.34 | 0.78 | 2.01 | 3.09 | |
| a | 13.87 | 0.49 | −0.97 | 0.04 | −0.86 | |
| Sy | 1.78 | 1.47 | −0.04 | 0.83 | 2.01 | |
| Kl | 3.26 | 6.21 | 0.75 | 1.91 | 3.13 | |
| Uv | 1 | 2.49 | 0.89 | 2.49 | 3.25 | |
| Am | 10.81 | 19 | 0.7 | 1.76 | 3.11 | |
| Ka | 0.37 | 0.01 | −0.97 | 0.04 | −2.04 | |
| Ku | 7.74 | 21.41 | 0.94 | 2.76 | 3.71 | |
| Oy | 0.08 | 0.01 | −0.86 | 0.16 | 1.27 | |
| tk2 | 0.39 | 0 | −1 | 0 | 0 | |
| al | 0.41 | 0 | −1 | 0 | 0 | |
| Uc | 7.23 | 0.72 | −0.91 | 0.1 | 0.44 | |
| f | 0.89 | 0.11 | −0.89 | 0.12 | 1.76 | |
| tm2 | 2.22 | 0.09 | −0.96 | 0.04 | −1.72 | |
| tl1 | 0.76 | 0 | −1 | 0 | −2.77 | |
| S | 10.01 | 12.9 | 0.46 | 1.29 | 2.88 | |
| Ud | 2.86 | 0.72 | −0.76 | 0.25 | 0.1 | |
| tl2 | 2.51 | 0.49 | −0.82 | 0.19 | 1.2 | |
| c | 2.17 | 2.14 | 0.22 | 0.98 | 2.37 | |
| As | 0.08 | 0.26 | 1 | 3.27 | 3.12 | |
| W | 5.77 | 8.01 | 0.52 | 1.39 | 2.8 | |
| Sm | 0.56 | 0.04 | −0.94 | 0.07 | −2.88 | |
| Nd | 0.58 | 0.31 | −0.44 | 0.54 | 1.53 | |
| th2 | 1.13 | 0 | −1 | 0 | 0 | |
| tk | 5.41 | 0.03 | −1 | 0.01 | −3.89 | |
| Ue | 4.59 | 3.76 | −0.05 | 0.82 | 2.35 | |
| tm1 | 0.09 | 0 | −1 | 0 | 0 | |
| d | 0.13 | 0 | −1 | 0 | 0 | |
| Tv | 0.7 | 0 | −1 | 0 | 0 | |
| th1 | 0.17 | 0.19 | 0.33 | 1.12 | 2.44 | |
| Ks | 0.5 | 2.42 | 0.82 | 4.86 | 4.1 | |
| Ts | 0.01 | 0 | −1 | 0 | 0 | |
| Sv | 0 | 0 | −1 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, J.; Yunus, A.P.; Tien Bui, D.; Sahana, M.; Chen, C.-W.; Zhu, Z.; Wang, W.; Thai Pham, B. Evaluating GIS-Based Multiple Statistical Models and Data Mining for Earthquake and Rainfall-Induced Landslide Susceptibility Using the LiDAR DEM. Remote Sens. 2019, 11, 638. https://doi.org/10.3390/rs11060638
Dou J, Yunus AP, Tien Bui D, Sahana M, Chen C-W, Zhu Z, Wang W, Thai Pham B. Evaluating GIS-Based Multiple Statistical Models and Data Mining for Earthquake and Rainfall-Induced Landslide Susceptibility Using the LiDAR DEM. Remote Sensing. 2019; 11(6):638. https://doi.org/10.3390/rs11060638
Chicago/Turabian StyleDou, Jie, Ali P. Yunus, Dieu Tien Bui, Mehebub Sahana, Chi-Wen Chen, Zhongfan Zhu, Weidong Wang, and Binh Thai Pham. 2019. "Evaluating GIS-Based Multiple Statistical Models and Data Mining for Earthquake and Rainfall-Induced Landslide Susceptibility Using the LiDAR DEM" Remote Sensing 11, no. 6: 638. https://doi.org/10.3390/rs11060638
APA StyleDou, J., Yunus, A. P., Tien Bui, D., Sahana, M., Chen, C. -W., Zhu, Z., Wang, W., & Thai Pham, B. (2019). Evaluating GIS-Based Multiple Statistical Models and Data Mining for Earthquake and Rainfall-Induced Landslide Susceptibility Using the LiDAR DEM. Remote Sensing, 11(6), 638. https://doi.org/10.3390/rs11060638