An Automated Rectification Method for Unmanned Aerial Vehicle LiDAR Point Cloud Data Based on Laser Intensity
Abstract
:1. Introduction
2. Data and Methods
2.1. Study Area and Data Acquisition
2.2. Rectification of UAV LiDAR System Errors
2.2.1. LiDAR Georeferencing Equations
2.2.2. Boresight Alignment Model
2.3. Automated Rectification Based on the Laser Intensity
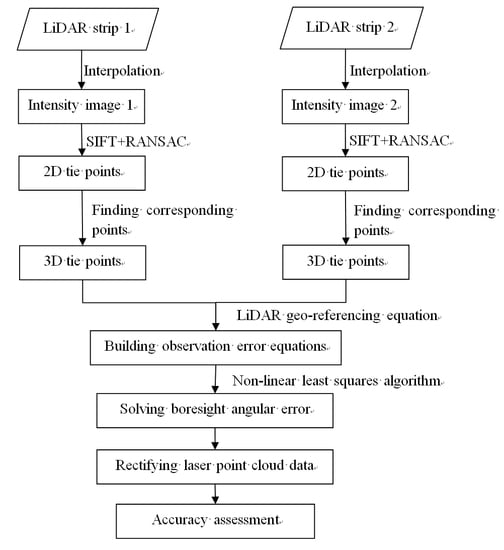
2.4. Workflow of Our Proposed Method
2.4.1. Generation of the Intensity Images
2.4.2. Tie Point Extraction in 2D Space
2.4.3. Refining Tie Point Sets in 3D Space
2.4.4. Estimation of Boresight Angular Error Parameters
3. Results
3.1. 2D Tie Points Extraction in the Case Study
3.2. 3D Tie Point Sets Construction with the Two Flight Lines
3.3. Correction of the Boresight Angular Error of the Two Strips
3.4. Accuracy Assessment
4. Discussion
4.1. The Influence of Parameter K
4.2. The Influence of Calibration Parameter on Geolocation Error
4.3. Influence of the Initial Values on Model Convergence
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chiang, K.W.; Tsai, G.J.; Li, Y.H.; El-Sheimy, N. Development of LiDAR-based UAV system for environment reconstruction. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1790–1794. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR system with application to forest inventory. Remote Sens. 2012, 4, 1519. [Google Scholar] [CrossRef]
- Kaňuk, J.; Gallay, M.; Eck, C.; Zgraggen, C.; Dvorný, E. Technical Report: Unmanned Helicopter Solution for Survey-Grade Lidar and Hyperspectral Mapping. Pure Appl. Geophys. 2018, 175, 3357–3373. [Google Scholar] [CrossRef]
- Chen, C.F.; Li, Y.; Zhao, N.; Yan, C. Robust interpolation of DEMs from LiDAR-derived elevation data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1059–1068. [Google Scholar] [CrossRef]
- Lin, Y.; Hyyppä, J.; Jaakkola, A. Mini-UAV-borne LIDAR for fine-scale mapping. IEEE Geosci. Remote Sens. Lett. 2011, 8, 426–430. [Google Scholar] [CrossRef]
- Kwan, M.P.; Ransberger, D.M. LiDAR Assisted Emergency Response: Detection of Transport Network Obstructions Caused by Major Disasters. Comput. Environ. Urban Syst. 2010, 34, 179–188. [Google Scholar] [CrossRef]
- Hou, M.; Li, S.K.; Jiang, L.; Wu, Y.; Hu, Y.; Yang, S.; Zhang, X. A new method of gold foil damage detection in stone carving relics based on multi-temporal 3D LiDAR point clouds. ISPRS Int. J. Geo-Inf. 2016, 5, 60. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Zhao, X.; Wu, F.; Li, Y.; Liu, J.; Chen, L.; Xu, G.; Lin, G.; et al. An integrated UAV-borne lidar system for 3D habitat mapping in three forest ecosystems across China. Int. J. Remote Sens. 2017, 38, 2954–2972. [Google Scholar] [CrossRef]
- Sankey, T.; Donager, J.; McVay, J.; Sankey, J.B. UAV lidar and hyperspectral fusion for forest monitoring in the southwestern USA. Remote Sens. Environ. 2017, 195, 30–43. [Google Scholar] [CrossRef]
- Wieser, M.; Mandlburger, G.; Hollaus, M.; Otepka, J.; Glira, P.; Pfeifer, N. A case study of UAS borne laser scanning for measurement of tree stem diameter. Remote Sens. 2017, 9, 1154. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Evans, J.S.; Martinuzzi, S.; Gessler, P.E.; Hudak, A.T. Characterizing forest succession with LiDAR data: An evaluation for the inland northwest, USA. Remote Sens. Environ. 2009, 113, 946–956. [Google Scholar] [CrossRef]
- Díaz-Varela, R.A.; De la Rosa, R.; León, L.; Zarco-Tejada, P.J. High-resolution airborne UAV imagery to assess olive tree crown parameters using 3d photo reconstruction: Application in breeding trials. Remote Sens. 2015, 7, 4213–4232. [Google Scholar] [CrossRef]
- Dan, J.; Yang, X.; Shi, Y.; Guo, Y. Random Error Modeling and Analysis of Airborne LiDAR Systems. Remote Sens. 2014, 52, 3885–3894. [Google Scholar]
- Glennie, C. Rigorous 3D error analysis of kinematic scanning LIDAR systems. J. Appl. Geod. 2007, 1, 147–157. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, X.; Zheng, M.; Huang, X. LiDAR strip adjustment using multi-features matched with aerial images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 976–987. [Google Scholar] [CrossRef]
- Hebel, M.; Stilla, U. Simultaneous calibration of ALS systems and alignment of multiview LiDAR scans of urban areas. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2364–2379. [Google Scholar] [CrossRef]
- Li, F.; Cui, X.; Liu, X.; Wei, A.; Wu, Y. Positioning errors analysis on airborne LIDAR point clouds. Infrared Laser Eng. 2014, 43, 1842–1849. [Google Scholar]
- Skaloud, J.; Lichti, D. Rigorous approach to boresight self-calibration in airborne laser scanning. ISPRS J. Photogramm. Remote Sens. 2006, 61, 47–59. [Google Scholar] [CrossRef]
- Bang, K.I.; Habib, A.; Kersting, A. Estimation of Biases in LiDAR System Calibration Parameters Using Overlapping Strips. Can. J. Remote Sens. 2010, 36, S335–S354. [Google Scholar] [CrossRef]
- Habib, A.; Kersting, A.P.; Bang, K.I.; Lee, D. Alternative methodologies for the internal quality control of parallel LiDAR strips. Canadian 2010, 48, 221–236. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef] [Green Version]
- Filin, S. Elimination of systematic errors from airborne laser scanning data. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 25–29 July 2005. [Google Scholar]
- Rodarmel, C.; Lee, M.; Gilbert, J.; Wilkinson, B.; Theiss, H.; Dolloff, J.; O’Neill, C. The universal LiDAR error model. Photogramm. Eng. Remote Sens. 2015, 81, 543–556. [Google Scholar] [CrossRef]
- Zhang, X.; Forsberg, R. Retrieval of Airborne LiDAR misalignments based on the stepwise geometric method. Surv. Rev. 2010, 42, 176–192. [Google Scholar] [CrossRef]
- Le Scouarnec, R.; Touzé, T.; Lacambre, J.B.; Seube, N. A new reliable boresight calibration method for mobile laser scanning applications. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 67–72. [Google Scholar] [CrossRef]
- Gallay, M.; Eck, C.; Zgraggen, C.; Kaňuk, J.; Dvorný, E. High resolution airborne laser scanning and hyperspectral imaging with a small UAV platform. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 823–827. [Google Scholar] [CrossRef]
- Filin, S. Recovery of systematic biases in laser altimetry data using natural surfaces. Photogramm. Eng. Remote Sens. 2003, 69, 1235–1242. [Google Scholar] [CrossRef]
- Schenk, T. Modeling and Analyzing Systematic Errors of Airborne Laser Scanners; Technical Notes in Photogrammetry; The Ohio State University: Columbus, OH, USA, 2001. [Google Scholar]
- Bäumker, M.; Heimes, F.J. New Calibration and computing method for direct georeferencing of image and scanner data using the position and angular data of a hybrid inertial navigation system. Proc. Natl. Acad. Sci. USA 2001, 97, 14560–14565. [Google Scholar]
- Marchant, C.C.; Moon, T.K.; Jacob, H.G. An Iterative Least Square Approach to Elastic-Lidar Retrievals for Well-Characterized Aerosols. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2430–2444. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant key points. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Wang, F.B.; Tu, P.; Wu, C.; Chen, L.; Feng, D. Multi-image mosaic with sift and vision measurement for microscale structures processed by femtosecond laser. Opt. Lasers Eng. 2018, 100, 124–130. [Google Scholar] [CrossRef]
- Guo, B.; Li, Q.; Huang, X.; Wang, C. An improved method for power-line reconstruction from point cloud data. Remote Sens. 2016, 8, 36. [Google Scholar] [CrossRef]








| Laser Scanner1 | Specifications | GNSS/IMU2 | Specifications |
|---|---|---|---|
| Minimum Range | 5 m | Positioning Mode | RTK |
| Pulse Repetition Rate | 550 KHz | Data Frequency | 100 Hz |
| Measurement Accuracy | 0.015 m | Position Accuracy(CEP) | H:0.02 m; V:0.03 m |
| Scanning Speed | 200 scan/s | Speed Accuracy | 0.1 km/h |
| Angle Resolution | 0.001° | Roll Accuracy (1σ) | 0.05° |
| Field of View | 330° | Pitch Accuracy (1σ) | 0.05° |
| Echo Signal Intensity | 16 bit | Heading Accuracy (1σ) | 0.10° |
| Method | Stepwise Geometric Method | Our Proposed Method | ||||
|---|---|---|---|---|---|---|
| Parameter | ω | ϕ | κ | ω | ϕ | κ |
| Estimated value | −1.050° | −0.2580° | −0.7980° | −0.7384° | −0.2245° | −0.7219° |
| Error | Planar RMSE/m | Elevation RMSE/m | ||||
|---|---|---|---|---|---|---|
| Method | Raw data | Stepwise geometric method | Proposed method | Raw data | Step-wise geometric method | Proposed method |
| Strip 1 | 0.060 | 0.049 | 0.050 | 0.024 | 0.015 | 0.014 |
| Strip 2 | 0.075 | 0.059 | 0.064 | 0.020 | 0.015 | 0.014 |
| Average | 0.068 | 0.054 | 0.057 | 0.022 | 0.015 | 0.014 |
| K value | Match count | ω/° | ϕ/° | κ/° |
|---|---|---|---|---|
| 20 | 13 | -0.7302 | -0.3353 | -2.3283 |
| 40 | 12 | -0.7366 | -0.2530 | -1.1801 |
| 60 | 12 | -0.7384 | -0.2507 | -1.1319 |
| 80 | 12 | -0.7373 | -0.2451 | -1.0975 |
| 100 | 12 | -0.7395 | -0.2382 | -0.9498 |
| 200 | 12 | -0.7384 | -0.2245 | -0.7219 |
| 300 | 11 | -0.7492 | -0.2951 | -1.6186 |
| 400 | 11 | -0.7500 | -0.2955 | -1.6275 |
| 500 | 10 | -0.7498 | -0.2490 | -1.6450 |
| Initial Value | Iteration Count | Converges to Same Value | ||
|---|---|---|---|---|
| ω/° | ϕ/° | κ/° | ||
| 0 | 0 | 0 | 3 | — |
| 10 | 0 | 0 | 4 | yes |
| 0 | 10 | 0 | 3 | yes |
| 0 | 0 | 10 | 3 | yes |
| 10 | 10 | 0 | 3 | yes |
| 10 | 0 | 10 | 3 | yes |
| 0 | 10 | 10 | 4 | yes |
| 10 | 10 | 10 | 4 | yes |
| 30 | 30 | 30 | 4 | yes |
| 60 | 60 | 60 | 6 | yes |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Gao, R.; Sun, Q.; Cheng, J. An Automated Rectification Method for Unmanned Aerial Vehicle LiDAR Point Cloud Data Based on Laser Intensity. Remote Sens. 2019, 11, 811. https://doi.org/10.3390/rs11070811
Zhang X, Gao R, Sun Q, Cheng J. An Automated Rectification Method for Unmanned Aerial Vehicle LiDAR Point Cloud Data Based on Laser Intensity. Remote Sensing. 2019; 11(7):811. https://doi.org/10.3390/rs11070811
Chicago/Turabian StyleZhang, Xianfeng, Renqiang Gao, Quan Sun, and Junyi Cheng. 2019. "An Automated Rectification Method for Unmanned Aerial Vehicle LiDAR Point Cloud Data Based on Laser Intensity" Remote Sensing 11, no. 7: 811. https://doi.org/10.3390/rs11070811
APA StyleZhang, X., Gao, R., Sun, Q., & Cheng, J. (2019). An Automated Rectification Method for Unmanned Aerial Vehicle LiDAR Point Cloud Data Based on Laser Intensity. Remote Sensing, 11(7), 811. https://doi.org/10.3390/rs11070811