4.1. Methods—Deriving the RFI Correction Scheme
The RFI correction scheme is based on the analysis of the scan-dependent bias and its evolution over the years. The overall idea is to use the RFI bias in the brightness temperature and to convert it to counts using the gain of the corresponding period. This is based on the two-point calibration equation, Equation (
3), from which we have
If we had
instead of
in Equation (
5), then there would be a change in
:
The approach of our correction scheme is to extract this from an observed bias for a sensor and a reference. The obtained counts correspond to the extra amount of recorded signals due to an RFI that we will have to subtract from the recorded . This count value (rounded to the nearest integer) is computed for each FOV such that we can finally provide a correction scheme for the Earth counts of each Earth view.
The details are described in the following paragraphs. An overview of the development of the RFI correction is given in
Figure 5.
An important aspect of the derivation of the correction is the definition of the RFI bias, which means the portion of the bias that can be assigned to RFI (see the upper parts of
Figure 5). From the global monthly mean biases used to investigate the scan dependence, the information of how much the sensors and MHS on NOAA-18 (reference
R) differ on average is obtained. However, this difference includes several aspects. First, it includes the difference due to the RFI impact. Hence, for the monthly mean bias we write
if the sensor is affected by RFI (
is used again to denote the contamination). However, the difference may also include instrumental issues not related to RFI. These are assumed to be constant over time and to, therefore, cancel out in the following steps. This is a necessary assumption at this point. Moreover, the difference includes effects due to the sampling of different phases of the diurnal cycle. These effects are smaller for the sounding channels than for the surface channels, and therefore, this method is only used for the sounding channels. From the listed contributions to the overall inter-satellite bias, the RFI contribution is extracted as follows. A month of a specific year is chosen where the RFI pattern is weakest (see
Figure 2b,c for 2005 for NOAA-16 and 2009 for NOAA-19, respectively). This month
is then defined as RFI-free
(which is not necessarily true, as there might be a small impact still). Computing the bias change from the reference month
to any month
m gives
At this point, it is assumed that all other instrumental issues causing biases are constant in time. Our second assumption is that possible changes in the monthly mean differences due to variations in the diurnal cycle from month
to month
m are negligible. (The validity of this assumption is ensured in the instrument-specific definition of the correction; see next paragraphs.) With the two assumptions, the expressions in parentheses in Equation (
11) cancel to yield
Any change
in the bias between the sensor and the reference with respect to this reference month
is, therefore, defined as the RFI bias:
In the worst case, this would include a contribution due to the diurnal cycle, and we would erroneously remove the diurnal cycle differences when later applying the correction . Hence, we need to be more careful and specific in the definition of the correction based on this RFI bias for the individual instruments in order to keep the contribution from the diurnal cycle as small as possible.
The instrument-specific definition of the correction is depicted in the lower part of
Figure 5. The deduction of the correction started with studying the monthly mean bias of the instrument and the reference
over the duration of the mission. By studying the plots of the monthly mean bias
like
Figure 3 (for NOAA-16) and
Figure 4 (for NOAA-19) for all years of the respective mission, we were able to deduce whether the RFI pattern remained constant or changed over time.
For MHS on NOAA-19, we identified distinct periods of constant RFI impact (see
Section 3.2.2). Hence, we only needed a constant correction per period. Each of these corrections was obtained from the RFI bias (bias change with respect to reference month April 2009) for all months of the first year in the specific period. We chose April 2009, since the RFI impact in this month was weak and the unstable phase of summer 2009 only started later. The correction (per month) of the first year
in the specific period
was then used as a correction for the respective months of all other years in the period. Hence, for all years of period
where month
m is Jan, Feb, ... Dec, and
denotes the median gain of the sensor in month
m of the first year
in the respective period
. See
Table 1 and
Figure 6 for the applied correction scheme on Earth view counts. As the analysis of the scan-dependent bias has shown, the impact of the diurnal cycle effects (that translate to seasonal cycle effects in the monthly means) was smaller than the RFI impact and only emerged for the later years when NOAA-19 and the reference NOAA-18 drifted apart. Since the RFI-correction is based on the first year of each period, even the correction for the third period
from December 2011 to 2017 was based on the relatively early year 2012, when the impact of the diurnal cycle effects was small. Hence, the applied derivation to obtain the RFI correction ensured a reduced contribution from the diurnal cycle effects.
For NOAA-16, no clear periods of constant RFI pattern were identified (see
Section 3.2.1). Rather, the pattern changed continuously over time to a further increased positive bias for FOVs around nadir and a further increased negative bias towards FOVs at the left edge of the scan (see
Section 3.2.1), superimposed with a general increase in the absolute value of the bias over time. This behaviour does not allow for a clear definition of periods suitable for a constant correction. Hence, we defined the RFI bias as the difference in the bias of each individual month with respect to the reference month, October 2005. Consequently, each month and year received an individual correction:
See
Table 2 and
Figure 7 for the applied correction scheme on Earth view counts. This approach of individual, monthly RFI corrections, in general, overcorrected the differences due to diurnal and seasonal cycle effects, which should not be removed. However, the impact from RFI was much larger than these natural effects. In the bias analysis, we observed that the bias change did not follow a seasonal pattern but followed only the evolution of the increasing RFI impact as a consequence of the decreasing gain (see
Section 3.2.1). Hence, in light of the dominating RFI impact, the effect of neglecting this possible overcorrection is small. It grows over time as the gain decreases because any bad correction value on the count level has an increasing impact when the gain decreases. This was accounted for in our uncertainty estimates.
Having defined the instrument-specific RFI correction, it can be applied in our calibration processing. The correction is defined as
and rounded to the nearest integer. It is added to the contaminated Earth counts for each individual pixel (single measurement within a scan line within an orbit) as
where
contains the correction for each FOV and the corresponding month the pixel belongs to.
The uncertainty estimate on our RFI correction scheme is twofold. First, the imperfection of the reference month is accounted for, which may be contaminated by RFI already (this is indeed probable). As the uncertainty estimate, the standard deviation over the FOVs of the reference month is used. This may provide a first indication of the initial RFI contamination. For NOAA-16, for channels 3–5, values of 0.20, 0.27, and 0.49 K were respectively obtained. For NOAA-19, for channels 3 and 4, values of 0.08 and 0.11 K were obtained, respectively. On top of that, a further uncertainty estimate related to a possible erroneous elimination of diurnal cycle effects is conducted. The standard deviation of the correction in counts over the months and FOVs is used. This uncertainty in counts then scales with the gain to an uncertainty estimate of the brightness temperature. This uncertainty estimate was about 0.1 K for NOAA-19, and it varied for NOAA-16 from 0.1 K in the early years to 1 K in 2011, which was correlated to the decrease in gain.
4.2. Results—RFI-cCrrected NOAA-16 and NOAA-19
The RFI correction scheme for NOAA-16 and NOAA-19 provided a value to be added to the Earth counts for each FOV, channel, and period of constant RFI. This extra proportion of counts was added to the Earth counts before any quality checks were executed in our processing chain for the FCDR (fundamental climate data record) generated within the Horizon 2020 project FIDUCEO (Fidelity and uncertainty in climate data records from earth observation) [
12]. The calibration was then executed using these modified Earth counts in the measurement equation. Hence, the whole archive of the level 1b NOAA-16 and NOAA-19 data was recalibrated from the raw data, finally providing an RFI-corrected record of the brightness temperature.
The performance of this RFI correction is analysed in the following text.
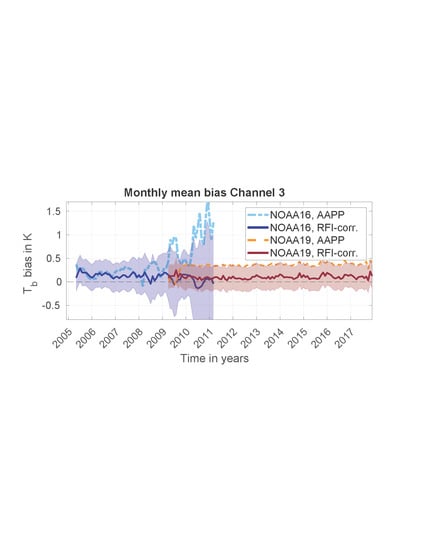
Figure 8 shows the global monthly mean bias as a function of time for the operational data (AAPP processed; dashed lines in
Figure 8) and the RFI-corrected data (FIDUCEO FCDR processing; solid lines) for channels 3–5, together with the estimated uncertainties. A distinct improvement in terms of the stability and consistency to NOAA-18 was achieved. The strong bias increases for NOAA-16 (blue curves) were mitigated. The uncertainty of the applied correction indicates that the corrected data agree with NOAA-18. Small differences occurred because of an unsuited antenna pattern correction used for NOAA-18 in AAPP [
12] and because of the different LECT of the satellites. The difference in LECT causes an overall offset of the instruments that varies slightly over time as the satellites drift, and it also induces the seasonal changes with an increasing amplitude for the times with increasingly different LECT. These remaining small differences also show that the RFI-correction does not erroneously remove the diurnal cycle effects. Overall, a stable improvement with respect to the uncorrected data was visible.
The correction for MHS on NOAA-19 (red curves in
Figure 8) was also successful. Channel 3 agrees with NOAA-18 for the uncertainties (
Figure 8a). The large stable offset against NOAA-18 was reduced. As for NOAA-16, the remaining small difference was due to the wrong antenna pattern correction being applied on NOAA-18 in the AAPP-processed data. This improved in our FCDR production presented in Reference [
12]. The uncertainties due to common effects displayed as a shaded region still include the AAPP data at their upper bound. This is not an intention of the design of the RFI correction but a result of the combination of all the estimated uncertainties due to common effects (see References [
12,
13]). The RFI impact was much weaker for channel 4 (
Figure 8b), and therefore, no obvious improvement was visible, as is the case for channel 3. In summer 2009, the AAPP processing provided a slightly smaller bias than the RFI-corrected data. This is also visible for channel 3. During this period, NOAA-19 was very unstable, with several interventions by the instrument control on the ground [
14], such that the RFI correction scheme was not expected to mitigate the RFI effect correctly. This period is not part of the FCDR presented in Reference [
12]. Note that channel 5 is not RFI-corrected, and therefore, our processed data agree with the AAPP data (hence, the AAPP curve is hidden behind our data in
Figure 8c). Finally, it should be noted that the applied RFI correction did not erroneously remove the diurnal/seasonal cycle effects, as we saw an increased amplitude for the seasonal cycle towards later years.