Resolutional Analysis of Multiplicative High-Frequency Speckle Noise Based on SAR Spatial De-Speckling Filter Implementation and Selection
Abstract
:1. Introduction
2. Concepts and Methods
2.1. SAR Received Backscattered Signal Modeling
2.2. Multiplicative Speckle Noise Behaviroal Formulation and Modeling
2.3. De-Speckled Image HMS Noise Behavioral Modeling
2.4. HMS System Resolution Extraction Method Concept
3. Resolutional Analysis Results
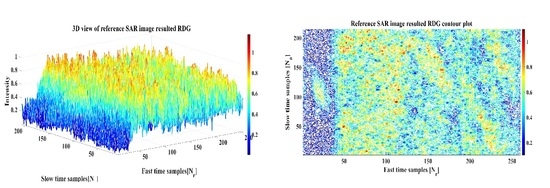
3.1. HMS System Resolution Analysis Based on RDG Extraction
3.2. HMS System Resolution Analysis Based on RFP Extraction
3.3. HMS Image Resolution Analysis Based on Objective Quality Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barnes, C.F. Synthetic Aperture Radar: Wave Theory Foundations, Analysis and Algorithms; Barnes: Powder Spring, GA, USA, 2015. [Google Scholar]
- Chen, K.S. Principles of Synthetic Aperture Radar Imaging; Taylor & Francis Group: Boca Raton, London, UK, 2016. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data; Artech House: Boston, MA, USA, 2005. [Google Scholar]
- Argentini, F.; Lapini, A.; Bianchi, T.; Alparone, L.A. Tutorial on speckle reduction in synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2013, 1, 6–35. [Google Scholar] [CrossRef]
- Liu, F.; Wu, J.; Li, L.; Jiao, L.; Hao, H.; Zhang, X. A hybrid method of SAR speckle reduction based on geometric-structural block and adaptive neighborhood. IEEE Trans. Geosci. Remote Sens. 2018, 56, 730–748. [Google Scholar] [CrossRef]
- Yahya, N.; Kamel, N.S.; Malik, A.S. Subspace-based technique for speckle noise reduction in SAR images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6257–6271. [Google Scholar] [CrossRef]
- Di Martino, G.; Simone, A.D.; Lodice, A.; Ricco, D. Scattering-Based nonlocal means SAR despeckling. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3574–3588. [Google Scholar] [CrossRef]
- Gleich, D. Optimal-Dual-Based l1 Analysis for Speckle Reduction of SAR Data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6674–6685. [Google Scholar] [CrossRef]
- Di Martino, G.; Lodice, A.; Riccio, D.; Ruello, G. Equivalent number of scatterers for SAR speckle modeling. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2255–2564. [Google Scholar] [CrossRef]
- Zhao, W.; Deledalle, C.A.; Denis, L.; Maître, H.; Nicolas, J.M.; Tupin, F. Ratio-based multitemporal SAR images denoising: RABASAR. IEEE Trans. Geosci. Remote Sens. 2019, 1–14. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shunmugan, K.S.; Holtzman, J.C. A Model for Radar Images and Its Application to Adaptive Digital Filtering of Multiplicative Noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, 4, 157–166. [Google Scholar] [CrossRef]
- Lee, J.S. A Simple Speckle Smoothing Algorithm for Synthetic Aperture Radar Images. IEEE Trans. Syst. Man Cybern. 1983, 13, 85–89. [Google Scholar] [CrossRef]
- Kuan, D.; Sawchuk, A.; Strand, T.; Chavel, P. Adaptive Restoration of Images with Speckle. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 373–383. [Google Scholar] [CrossRef]
- Touzi, R. A review of speckle filtering in context of estimation theory. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2392–2404. [Google Scholar] [CrossRef]
- Goodman, J.W. Speckle phenomenon in optics: Theory and applications. J. Stat. Phys. 2008, 130, 413–414. [Google Scholar]
- Amirmazlaghani, M.; Amindavar, H. A novel sparse method for despeckling SAR images. IEEE Trans. Geosci. Remote Sens. 2012, 50, 5024–5032. [Google Scholar] [CrossRef]
- Di Martino, G.; Poderico, M.; Poggi, G.; Riccio, D.; Verdoliva, L. Benchmarking Framework for SAR Despeckling. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1596–1615. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Denis, L.; Poggi, G.; Tupin, F.; Verdoliva, L. Exploiting patch similarity for SAR image processing: The nonlocal paradigm. IEEE Signal Process. Mag. 2014, 31, 69–78. [Google Scholar] [CrossRef]
- Lang, F.; Yang, J.; Li, D. Adaptive-Window polarimetric SAR image speckle filtering based on a homogeneity measurement. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5435–5446. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.G.; Zhang, B.; Hong, W.; Wu, Y. Adaptive total variation regularization based SAR image despeckling and despeckling evaluation index. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2765–2774. [Google Scholar] [CrossRef]
- Wang, Y.; Ainsworth, T.L.; Lee, J.S. Application of mixture regression for improved polarimetric SAR speckle filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 453–467. [Google Scholar] [CrossRef]
- Ozcan, C.; Sen, B.; Nar, F. Sparisity-driven despeckling for SAR images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 115–119. [Google Scholar] [CrossRef]
- Ma, X.; Wu, P.; Shen, H. A nonlinear guided filter for polarimetric SAR image despeckling. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1918–1927. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Pan, X.; Gu, Z.; Wang, G. Raw signal simulator for SAR with trajectory deviation based on spatial spectrum analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6651–6665. [Google Scholar] [CrossRef]
- Ni, W.; Gao, X. Despeckling of SAR image using generalized guided filter with Bayesian nonlocal means. IEEE Trans. Geosci. Remote Sens. 2016, 54, 567–579. [Google Scholar] [CrossRef]

















| Column | De-Speckling Filter | Value |
|---|---|---|
| 1 | Gamma | 25.5 dB |
| 2 | Lee | 22 dB |
| 3 | Local sigma | 20.5 dB |
| 4 | Frost | 18.4 dB |
| 5 | Local adaptive median | 14.4 dB |
| 6 | Kuan | 14.1 dB |
| 7 | Lee sigma | 12.2 dB |
| Column | De-Speckling Filter | Value |
|---|---|---|
| 1 | Local sigma | 0.14 dB |
| 2 | Kuan | 0.14 dB |
| 3 | Local adaptive median | 0.18 dB |
| 4 | Lee sigma | 0.31 dB |
| 5 | Frost | 0.36 dB |
| 6 | Lee | 0.60 dB |
| 7 | Gamma | 0.62 dB |
| Parameter | Value |
|---|---|
| Carrier frequency | 14 GHz |
| Repetition frequency | 5 KHz |
| Sampling frequency | 180 MHz |
| Pulse width | 0.8 sec |
| Bandwidth | 140 MHz |
| Chirp scale factor | 1 |
| Image | MSE | MIV | Var. | SNR [dB] | PSNR [dB] | SSIM | MSSIM |
|---|---|---|---|---|---|---|---|
| Reference | - | 0.46 | 0.05 | 12.459 | - | - | - |
| Frost | 0 | 0.49 | 0.05 | 12.459 | - | 1 | 0.9903 |
| Gamma | 0 | 0.49 | 0.05 | 12.63 | - | 1 | 0.9903 |
| Kuan | 0.04 | 0.50 | 0.04 | 13.67 | 13.60 | 0.9153 | 0.9839 |
| Lee | 0.04 | 0.57 | 0.06 | 11.94 | 14.41 | 0.9506 | 0.9853 |
| Lee sigma | 0.06 | 0.61 | 0.05 | 12.62 | 12.58 | 0.9449 | 0.9825 |
| Local adaptive | 0.05 | 0.51 | 0.05 | 12.30 | 13.44 | 0.9477 | 0.9837 |
| Local sigma | 0.03 | 0.49 | 0.05 | 12.63 | 14.61 | 0.9675 | 0.9852 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heidarpour Shahrezaei, I.; Kim, H.-c. Resolutional Analysis of Multiplicative High-Frequency Speckle Noise Based on SAR Spatial De-Speckling Filter Implementation and Selection. Remote Sens. 2019, 11, 1041. https://doi.org/10.3390/rs11091041
Heidarpour Shahrezaei I, Kim H-c. Resolutional Analysis of Multiplicative High-Frequency Speckle Noise Based on SAR Spatial De-Speckling Filter Implementation and Selection. Remote Sensing. 2019; 11(9):1041. https://doi.org/10.3390/rs11091041
Chicago/Turabian StyleHeidarpour Shahrezaei, Iman, and Hyun-cheol Kim. 2019. "Resolutional Analysis of Multiplicative High-Frequency Speckle Noise Based on SAR Spatial De-Speckling Filter Implementation and Selection" Remote Sensing 11, no. 9: 1041. https://doi.org/10.3390/rs11091041
APA StyleHeidarpour Shahrezaei, I., & Kim, H. -c. (2019). Resolutional Analysis of Multiplicative High-Frequency Speckle Noise Based on SAR Spatial De-Speckling Filter Implementation and Selection. Remote Sensing, 11(9), 1041. https://doi.org/10.3390/rs11091041