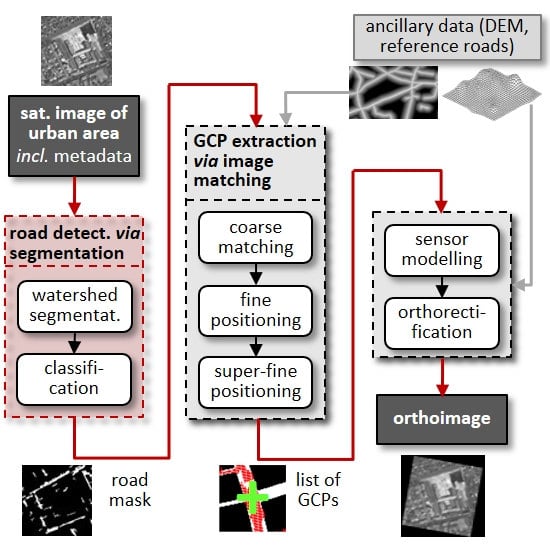
1. Introduction
Space and in particular satellite technologies are progressing very quickly. An increasing number of satellites are capable of imaging in very-high spatial resolution (VHR) of 2 m and less. Although large and heavy satellites currently exclusively provide VHR imagery, the trend is also shifting towards smaller satellites that will probably enter the VHR market in the coming years [
1]. Besides the increasing quantity of satellites that are able to acquire images in VHR, a very important aspect is also enhancing the image resolution. Currently, commercial satellites can provide panchromatic spatial resolutions of up to 0.3 m, which is hardly a limit that will not be surpassed in the future.
The increasing quantity of satellite data leads to the need for processing procedures that work (semi)automatically, and generate products with high accuracy. Only automatic processing chains can adequately fulfil the requirements for many applications that work with remote sensing. Among those applications, the ones that work mostly or only with VHR data are rapidly increasing and they usually demand fast delivery of already pre-processed satellite data.
The main pre-requisite for any successful information extraction from remotely sensed images is the accurate geometric processing of such data. Therefore, it is essential to geometrically correct all of the unrectified satellite images first. The accuracy and speed of the corrections are of the outmost importance in present-day applications when huge amount of VHR data is available (a single VHR satellite can acquire more than 600,000 km
2 of images per day). For this reason, several automatic image registration methods have been developed in recent times (e.g., [
2,
3,
4,
5,
6]). These methods are commonly composed by two important processes: ground control points (GCPs) extraction and geometric transformation (modelling).
Automatic GCP extraction is done by image matching methods. These methods can be roughly divided into two groups: area-based and feature-based [
7]; within the remote sensing domain, the two approaches are often combined at different levels [
8]. These methods that are image intensity-based usually require that the target satellite image be compared to an already georeferenced reference image. The correspondence is usually done using local image features, such as SIFT (Scale-Invariant Feature Transform) [
9], but problems may arise when matching multi-temporal or multi-sensor images [
10]. Some of the feature-based methods extract GCPs with an object-level processing approach. In these methods, objects are extracted from the input image and are matched to reference digital data. The road network is taken in most circumstances for the reference digital data, since it is a stable structure that lies on the ground (Earth’s surface) and is easily visually recognised. The reference roads can be found in national topographic databases or web databases (e.g., OpenStreetMap). Although several studies addressed this topic (e.g., [
11]), it has rarely been extensively studied and utilized in practical applications [
12]. Newer matching methods also work on more complex descriptors (e.g., [
13].
The road extraction from a VHR image, which is also used in our solution, is a challenging issue and is very important for urban design and planning, navigation, traffic monitoring, and image registration in general [
14]. The topic of road extraction is of great significance and many algorithms were proposed in the last decades. Quackenbush [
15] already reviewed the techniques of extracting linear features from imagery that can be used also for road extraction. Wang et al. conducted a more recent review of road extraction from remote sensing [
16]. Among the road detection methods, the region-based techniques [
17] are widely used and they can effectively extract linear features with segmentation and classification [
18,
19]. Due to the wide variations of road types (e.g., city, rural) and the occlusion problems due to buildings, shadows, trees, vehicles, and other objects, these kind of techniques have several problems and often fail when dealing with complex road networks [
17]. For urban areas, some of the mentioned problems can be surpassed with applying graph-theory onto extracted features [
20].
Various functions can be employed for the geometric transformation [
21]. Physical transformation models are usually preferred, while the empirical models provide a good—and less complex—alternative. Therefore, the empirical rational function model (RFM) is commonly used for the geometric correction of commercial VHR satellites.
Various automatic geometric correction procedures utilize the RFM. Oh and Lee [
22] developed an algorithm for automatic bias-compensation of rational polynomial coefficients (RPCs) that are based on topographic maps. Their matching accuracy was approximately one pixel. Kartal et al. [
23] automatically orthorectified Pléiades imagery with a SIFT-based RPC refinement. Images with low incidence angles provided higher accuracy (better than 1 m) and a greater number of GCPs. Long et al. [
24] used the SIFT algorithm to automatically georeference the remotely-sensed images of spatial resolutions from 30 m to 2 m. Although many other studies addressed the problem of automatic geometric corrections, it is still challenging to deliver the georeferenced VHR panchromatic images with a high spatial accuracy (pixel and less), regardless of the images acquisition date and incidence angle. The challenge is even bigger when addressing images with (predominantly) urban land cover.
Commonly, the final goal of any automatic processing chains is the generation of geometrically corrected images through orthorectification. While the precise automatic orthorectification of medium and high resolution optical satellite images is already viable, a development of a robust procedure to obtain an accurate geometric correction of VHR panchromatic images is still challenging.
This paper presents a completely automatic workflow for the generation of orthoimages from very-high resolution optical panchromatic satellite images. The workflow is composed of an automatic GCPs extraction procedure that works in various steps and it uses image matching techniques and precise feature extraction algorithms, geometric modelling with a RFM, and orthorectification. The research is focused on densely populated urban areas, composed of their typical elements, such as high buildings, their shadows, and wide streets, which present a great challenge in terms of feature extraction and matching.
The aim of this study is to implement a procedure for a relatively fast extraction of GCPs with sub-pixel accuracy on different VHR panchromatic images of different dates and off-nadir angles that represent the urban areas to perform GCP refinement and precise orthorectification.
Section 2 describes the algorithm and procedures of the automatic geometric corrections.
Section 3 deals with the tested data and the evaluation methodology.
Section 4 presents the results of the geometric corrections on a set of VHR panchromatic Pléiades images.
Section 5 discusses the outcomes, and
Section 6 draws the conclusion.
2. Automatic Geometric Corrections
The proposed automatic geometric correction workflow is a result of an upgrade of the STORM geometric correction module that is described in [
25]. STORM is a fully automatic image processing chain that performs all of the processing steps from sensor-corrected or ortho-ready optical satellite images to web-delivered map-ready products. Modules of a pre-processing stage and the final product stage compose the chain. One of the most important pre-processing modules is the geometric corrections module. This module automatically generates orthoimages from various high resolution (HR) and very-high resolution (VHR) images. The processing workflow varies slightly, depending on the input image resolution—see
Section 2.1—but it is always composed of three sub-modules: automatic extraction of GCPs that is based on matching the roads detected from satellite image onto either reference rasterized roads (two-step algorithm) or reference rasterized roads and orthophotos (three-step algorithm), which is followed by automatic sensor modelling, during which either the proprietary physical sensor model or RFM are utilised, and finally orthorectification.
While the algorithms and results for HR images were partly presented in [
26] and improved and adapted algorithms that also support VHR images up to 2 m were tested in [
25], this paper focuses on further improvements and upgrades to enable the processing of sub-meter panchromatic images of complex urban land cover (e.g., when a large portion of densely built city areas are present on the images). The most important improvements are made to the GCP extraction sub-module, which is the most critical automatic step.
2.1. Automatic GCP Extraction
2.1.1. Two and Three Step GCP Extraction Module – Summary
This section summarizes the workflow of the previous GCP extraction procedure that is described in [
25] and it is the backbone of the proposed procedure.
Section 2.1.2 describes the modifications and upgrades of the previous procedure.
The core of the previous automatic GCPs extraction module is a two-step matching algorithm that utilizes vector roads as a reference layer and it delivers GCPs for high resolution (HR) images. The matching is done between the reference road data and roads extracted from the satellite images.
The reference roads layer is pre-prepared once per each geographic extent. The available vector data sources are combined into a common rasterized reference layer (
Figure 1 left). For Slovenia, the main vector source is the National topographic databases of roads 1:5,000, which has a planar accuracy of 1 m and 60% coverage. The roads have the same accuracy as the national aerial orthophoto, which constitute the reference data for the testing of the presented procedure. A complementary source for the areas within Slovenia is the roads part of the Infrastructural Cadastre with a planar accuracy under 1 m for highways and from 1–5 m elsewhere. We use the OpenStreetMap (OSM) vector road data for the neighbouring countries. All vector road data is rasterized based on the road width attribute (National topographic bases) or road category attribute (Infrastructural Cadastre and OSM). Additionally, road distance maps, as well as crossroad locations, are also computed. Finally, all reference data are tiled based on a fixed tiling grid.
From the satellite image, roads are extracted with the morphological operator top hat, which is optimal for recognising brighter objects (i.e., roads) against the darker surroundings (
Figure 1 right). Usually extraction is far from perfect, however it usually delivers sufficient road-like objects. Prior to the matching, the extracted road image is tiled and initial affine transform based on metadata parameters is applied.
The actual matching is a two-step algorithm (
Figure 2). The first step is the coarse matching of extracted road image tiles onto reference road maps. A check between matching parameters of neighbouring tiles is applied for consistency. The second step is the fine positioning of individual GCPs. It starts with a presumption that every listed crossroad is a potential GCP. Therefore, small GCP chips around each crossroad are cropped from each coarsely matched tile, and the fine positioning to the reference road chips is applied for each chip. The described two-step workflow is repeated for each image tile. The two-step algorithm delivers a sufficient number of GPCs for images of various HR sensors, and proved to also be very robust and stable in the occurrences of imperfections, either in detected roads or reference data [
26].
The described two-step algorithm was not capable of delivering accurate GCPs for multispectral (MS) VHR images. Therefore, the module was upgraded with a third step, i.e., super-fine positioning (
Figure 2) of individual GCPs onto an aerial orthophoto. This final step utilizes least square matching (LSM) for sub-pixel positioning. The improved module was capable of delivering sufficient number of accurate GCPs for multispectral WorldView-2 and Pléiades images for resolutions around 2 m [
25].
2.1.2. Modifications of GCP Extraction Module for VHR Panchromatic Images
On panchromatic VHR images of resolution far below 2 m (e.g., panchromatic WorldView-1/-2/-3/-4 and Pléiades images have resolutions mostly between 0.3 and 0.8 m), the previous GCP extraction module was not capable of delivering accurate GCPs. The main problem proved to be the detection of roads from raw satellite images. Namely, the morphological filtering (top-hat) could easily detect road edges, even road markings; however, it failed to extract the whole sections of roads that are—at this resolution—several pixels wide.
The previous extraction of roads is replaced with a new method that combines object segmentation and classification algorithm to overcome this deficiency (
Figure 3). All the other parts of the GCP extraction modules remained mostly unchanged.
Although the proposed method takes more time (in average it needs almost 10x more processing time), it can accurately detect the road segments across their full width. The watershed transformation is used to segment the road network. Watershed transformation [
27,
28] is an efficient procedure for image segmentation with a morphological algorithm. It is recognised as a powerful method, because it has the advantage of speed and simplicity [
29].
The segmentation procedure implemented in the proposed algorithm works in four main steps:
First, the algorithm automatically detects the initial seeds for the region growing. The seeds are defined as the regional minima of a gradient image that is produced by edge detectors (differences at the boundaries). When generated, the gradient image is smoothed with a circular element where size is set relative to the image resolution. Additionally, a threshold is adaptively determined in the way that it only selects the seeds that are relevant for the image (based on resolution and radiometric range). The size of the smoothing element and the threshold determine the number and location of the seeds. In the end, the selected seeds are labelled.
A second gradient image is generated with sharp edges that constitute the limits of the final segments.
Starting from the seeds, region growing is then performed. The simultaneously growing patches result in a segmented image, where every segment is labelled and does not overlap with the neighbours.
The properties of the segments are computed and used in the classification part.
The generated segments need to be classified, so that only those that possibly represent road segments are retained. The matching process between the extracted and reference road mask is very robust and it does not need the extracted mask to contain the whole road network. On the contrary, just its fractions are sufficient. For this reason and to speed-up the process of identifying the road segments, only a basic decision tree classification is performed. Since the classification of roads that are only based on spectral data is not feasible on panchromatic images, the classification mainly focuses on geometric properties that usually represent roads (i.e., it identifies small elongated segments). There are three properties that are employed to classify the road segments:
Area: Is defined as the total number of pixels in the segment [
13]. A road has a relatively larger area when compared to other artificial objects.
Elongation: Is defined as the ratio between the major and minor axis of the segment [
13]. Additionally, the ratio between the segment bounding box axes and the ratio between the bounding box and segment area are computed to retain the segments in the shape of crossroads.
Brightness: Road segments have low variations in grey levels—the lower the standard deviation, the higher the possibility to represent a road [
20]. Road segments are also mostly darker than other objects [
13].
All of the described properties are set after the segmentation in an adaptive way and their values are dependent on the image metadata. The two geometric properties rely on the image spatial resolution, while the brightness property is based on the radiometric range of the image.
Finally, the selected segments are stored in a binary mask (
Figure 4). The final mask is far from perfect: the roads are missing due to occlusions (by buildings, trees, cars, etc.) and imperfect segment detection; other objects are present, because of their similarity to road patches (e.g., roofs). Image matching is possible despite numerous imperfections.
Figure 5 shows three GCP extraction examples. The first column presents the reference crossroad data chips; the second shows the same crossroads as detected from the satellite image; the third demonstrates the coarse matching results between the corresponding data; the fourth exhibits the fine positioning results; and, the last presents the final matching position after super-fine positioning (here, the detected roads are superimposed to the orthophoto chip of a smaller size than the reference crossroad chips). Example (a) presents the ideal case, where the detection is perfect and its result is easily matched to the reference crossroad. Example (b) has two starting problems: the reference data is outdated (a new road is missing in the lower-right part) and the detection is incomplete. Nevertheless, the matching is still successful and it resulted in a GCP. Example (c) is taken from a highly urbanised area. In this case, the detection is inexact: two side roads are missing and the main road is only partially extracted, mainly due to occlusions (e.g., cars, trees). Despite all of these imperfections, the matching still produced an accurate GCP.
2.2. Geometric Modelling
After the GCPs extraction algorithm, the geometric correction is continued with the geometric modelling and finally orthorectification.
Figure 6 presents the workflow. The list of GCPs that were obtained from the GCP extraction procedure is additionally filtered with gross error removal algorithms that produce the final set of GCPs to refine the rational function geometric model. The bias-corrected results are then used in the orthorectification to generate the orthoimage.
2.2.1. Rational Function Model
The geometric corrections are done with a rational function model (RFM). The RFM is an empirical model and it provides a good alternative to the physical model with equivalent results [
30,
31]. Although the model is not so sensitive to GCPs distribution and their number, it is still advisable to only use high quality points that are scattered over the whole image. The RFM uses a ratio of two polynomial functions to compute the row and column image coordinates (
r,
c) from the object space ground coordinates (usually latitude (
Φ), longitude (
λ), and height (
h)) [
32]. To compute the coordinates, the functions use vendor-provided rational polynomial coefficients (RPCs), which are estimated using the physical model parameters (the satellite image vendors usually supply 20 RPCs for polynomials in both numerators and denominators). The implemented geometric correction can work with a single image or a block of images with a joint adjustment. In the latter case, GCPs that are common to all images are selected during the extraction algorithm that always targets the same crossroads. In this study, the single-image workflow (
Figure 6) is used to ensure that each image results are unbiased and not correlated to the others.
2.2.2. Gross Error Removal
The RFM implementation is straightforward. Although the RPC coefficients are quite accurate, they have to be bias-corrected first with at least few GCPs that ensure high accuracy throughout the resulting image. The correction starts with all of the extracted GCPs. Despite the automatic detection being composed of many steps and intermediate accuracy checks, some GCPs can exhibit the gross errors that need to be removed before the model refinement. Gross error removal is performed in two steps. First, the erroneous GCPs are eliminated based on the RANSAC algorithm [
33]. Roughly 10% of the GCPs are discarded according to the magnitude of their residuals that are obtained through the geometric model. Additionally, a simple gross error detection procedure is used that eliminates GCPs with residuals that differ by over 2σ from the mean value. The implementation of gross error removal in two steps is possible due to the high number of automatically detected GCPs.
2.2.3. Model Refinement
The remaining GCPs are used to correct the biases and random errors that are present in the supplied RPC coefficients. To remove the errors, the GCPs are introduced in refinement functions that are provided by the RPC adjustment equations [
34]:
Equations (1) and (2) are formed for each GCP, where Line and Sample are the measured image coordinates, () are object coordinates, Δp and Δr are refinement functions expressing the differences between the measured and the image coordinates calculated using RPCs, and are random errors, and p and r are the image coordinates obtained with RPCs.
Δ
p and Δ
r are the refinement functions expressed as first order polynomials to calculate six unknown adjustment parameters (
):
Each non-eliminated GCP is used to compute the six parameters with least square adjustment and that are later used to correct the pixel positions during orthorectification. The adjustment can work with a single image or a block of images. Currently, the supplied RPCs, the adjustment parameters and a suitable DEM can be used to orthorectify VHR images in the reference coordinate system by either an indirect or a direct method. The indirect method projects the pixels from the object space to the raw image, while the direct method works in the opposite direction [
26].
3. Test Data and Evaluation Methodology
3.1. Test Data
The developed procedure is tested on the Pléiades panchromatic images. The level of processing of all images is primary (sensor-corrected) with spatial resolutions from 0.7 m to 0.8 m, depending on the off-nadir viewing angle and with small deviations throughout the images. For the research, 14 images were acquired that cover two areas of interest (AOIs):
The first is named Ljubljana (LJ) and it comprises a dataset of six images of the Slovenian capital acquired during 2013 and 2014; area of the images is around 68 km2; and, four images were acquired during the same pass.
The second is named Kranj (KR) and the dataset has eight images of the city of Kranj that were taken in 2013; the images area is approximately 38 km2; and, the set is constituted by four stereopairs.
The images present mainly urban areas, but they also encompass agricultural land and hilly landscape with forests. Additional properties of the images can be seen in
Table 1; the first six images are from Ljubljana AOI, while the rest are from Kranj AOI.
3.2. Evaluation Methodology
The described research focuses on a fully automated process for optical image orthorectification. Its main part focuses on the extraction of GCPs in various steps to improve the accuracy of geometric correction for VHR panchromatic images. The acquired test images are processed in three different ways to better understand the contribution of the proposed extraction algorithm to the whole procedure: without GCPs, with GCPs that are extracted with the previous road mask detection algorithm, and with GCPs extracted with the proposed detection algorithm.
The test images from two AOIs exhibit different acquisition dates and off-nadir viewing angles, which range from 2.2° to 23.6° (
Figure 7). The images are acquired from all sides, which practically makes a lot of scenarios to test the road mask detection, as, for each angle, the buildings occlude different parts of the road network. Moreover, due to the varying acquisition dates, the images exhibit different shadow shapes that significantly influence the road extraction procedure.
Section 4.2 presents the relationship between the experimental results and the acquisition angle and time.
To only explore the impact of the densely built city area on the accuracy of the geometric corrections, the non-urban GCPs are removed. In this way, the results of the geometric model only reflect the accuracy of the extracted GCPs in those areas where the detection of points is very challenging.
Section 4.3 shows the results with only the urban GCPs.
The efficiency of the proposed algorithm is also tested with different number of GCPs and with two RPC refinement (correction) methods: affine and offset.
As the resulting orthoimages mostly reflect the accuracy of the geometric model results, they are not evaluated and presented in this paper.
4. Experimental Results
4.1. Geometric Model Results and Comparison of Different Extraction Methods
Table 2 presents the geometric model results of the proposed method. The number of GCPs (second column) represents the final number of points that are used in the correction of the RPCs. The number of extracted GCPs mostly depends on the image size, the off-nadir angle, and the acquisition date. It is reduced to the final number after the accuracy check and the gross error removal techniques. In our case, the RANSAC iterations assume that at least 90% of the points do not have gross errors or that the errors are negligible.
After the adjustment, the GCPs root mean square errors (RMSEs) are computed from the difference between the extracted coordinates and the coordinates that were obtained with the geometric model. To obtain more meaningful results for each image, 15 evenly distributed manual independent check points (ICPs) were measured through the images. The reference coordinates of the ICPs were manually measured on national aerial orthophotos with 0.5 m resolution. The achieved RMSEs, which were computed from the difference between the measured coordinates and the coordinates that were obtained with the geometric model, are around 1 pixel, and in four cases even reach sub-pixel values.
To test the accuracy of the proposed extraction method, the results of the geometric model that is based on the previous (original) GCPs extraction and based on the proposed GCPs extraction are compared to the results that were obtained without GCPs (unbiased RPC coefficients).
Figure 8 shows the results of this comparison. It can be clearly seen that the smallest RMSE is achieved by the proposed method for the majority of images. As expected, if no GCPs are used, the results are much worse in all cases and they mostly reach values that are also obtained by other studies (e.g., [
35]).
4.2. Results Regarding Date and Off-nadir Angle
Figure 9 presents the relationship between the obtained results and the off-nadir viewing angle and the time of acquisition. The connection is only examined between the RMSEs at ICPs of the two GCP extraction methods. Although the figure shows the results in ascending off-nadir viewing angle sequence, the RMSEs do not reflect this and suggest that there is no correlation between the two parameters. The same conclusion can be drawn for the acquisition dates.
4.3. Results of GCPs Inside City Perimeter
As mentioned in
Section 3.1, the acquired images also contain agricultural land and forest patches aside from urban areas. The share of the densely populated city area is 49% for the Ljubljana images, while the percentage is lower for the Kranj images—around 21%. To only analyse the accuracy of the GCP extraction in city areas, the geometric model is only tested with GCPs that are located inside the city perimeter.
Figure 10 shows two examples of GCP distribution with the city perimeter taken into account.
Table 3 presents the geometric model results when only GCPs located inside the city perimeter are used. As expected, in this case, all of the values are worse when compared to the results where all of the GCPs are used; the most significant indicators—RMSEs at ICPs—are above one pixel, except for one image.
Figure 11 graphically presents the results. Besides the results with the proposed method, the previous method results are also displayed to emphasise the difference of GCP extraction performance in urban environments. For all images, the proposed method greatly improves the performance of the previous method. The RMSE is at least twice smaller in many cases, while, in few cases, the previous method achieves errors even above five pixels. The numbers above the bars denote the decrease in accuracy when only GCPs that are inside the city perimeter are used. As expected, the values are higher for both methods and all images. The decrease is minimal for the proposed method (never exceeding 1 pixel), while the changes for the previous method are substantial and they are rarely less than 0.5 pixel.
The accuracy results are also correlated to the number of GCPs.
Figure 12 shows the final number of GCPs that are used in the geometric model after the gross error removal techniques. The graph presents the numbers for both road extraction methods with and without the reduction of the number of GCPs to the city perimeter area. The proposed method extracts significantly more GCPs than the previous method. The number of extracted GCPs seems to be approximately proportional to the image area, which is not true for the previous method that has obvious problems in detecting GCPs in built areas. The proposed method extracts, on average, more than 150 GCPs for the Ljubljana AOI and more than 100 for the Kranj AOI. The corresponding numbers for the previous method are usually less than 50. Note that all other processing parameters are kept unchanged.
4.4. Results with Different Numbers of Used GCPs and RPC Refinement Methods
The geometric corrections of satellite data with RFMs can be done with various methods. The most common is the model refinement (correction) with affine parameters (as presented in
Section 2.2.3.). Another popular method is the bias correction with offsets. This method is very simple and it only translates the pixels by the same value on each of the axes. Although the method is simple and fast, it can perform even better than the affine with some satellites.
Figure 13 presents the difference between the results that were obtained with both refinement methods. The comparison is only performed between the RMSEs at ICPs. The results indicate that both of the methods perform with similar accuracies. It can be concluded that, when high number of GCPs are used, both methods can be utilized with Pléiades imagery.
Different numbers of GCPs are used in the correction to test the behaviour and robustness of the proposed algorithm. For each image, decimating the initial set when considering the point quality (from image matching) and even the distribution of the points in the image generates various sets of GCPs. Every set has a different number of points ranging from over 200 to 9. For comparison purposes, all of the obtained point sets are used in the geometric model with both the affine and offset refinement methods.
Table 4 lists the test results for two selected images. The first image is from the Ljubljana AOI, while the second is from Kranj AOI. RMSEs at GCPs are mostly in the same range, while there is a small decrease in accuracy at ICPs when sets with less than 30 points are used. This is only valid for the affine refinement as the offset methods present mostly unchanged RMSEs for all the sets.
5. Discussion
We upgraded the previous automatic GCPs extraction algorithm, which originally performed well for VHR images up to resolutions of around 2 m, with the aim to also work successfully for panchromatic VHR images with resolutions up to 0.3 m. The upgrade concentrated on the road detection method, which left all other parts mostly unchanged.
The results demonstrate the ability of the proposed automatic extraction method to obtain GCPs with sub-pixel accuracy. The GCPs residuals are below 1 pixel for all 14 test Pléiades images, while their RMSEs are mainly just above 1 pixel (
Table 2). Very similar results can be seen when manual ICPs are employed. Although there are some outliers, the majority of residuals are around 0.5 pixels, which results in final RMSEs that are even lower than those achieved with GCPs. This indicates that small random errors are still present in GPCs, but, as there are no systematic errors generated by the extraction algorithm, the high number of points can still compensate for random errors. The precision of the extracted points can be hardly visually evaluated on the produced GCP chips images since the sub-pixel accuracy level is reached (see
Figure 5).
The proposed method outperforms the previous GCP extraction method, which uses a different road detection algorithm. The previous method has problems in detecting broad roads and roads in densely built areas. It only performs slightly better in Kranj AOI images where the percentage of urban areas is lower when comparing it with the proposed method. This statement is supported by the tests that were performed with the GCPs inside the city perimeter. The results, when using only points inside the urban areas, are unusable in most cases when the points are extracted by the previous method. In those cases, the ICP RMSEs are not correlated to the image size or AOI. Although the number of GCPs in Kranj images is relatively high (and mostly higher than in Ljubljana images with almost twice the area), they are significantly reduced when confining them to the city area. Although the city area is around 21% of the image, only 14% of points are present in this area. For the proposed method the percentage is 31%, which means that relatively more points are present within the boundaries of the city. It can be concluded that the previous method can achieve slightly better results than the proposed method with only GCPs extracted in predominantly non-urban areas where the roads are narrower and can be easily separated from the background that is mostly composed by vegetation. Some images achieve worse results than with the unbiased RPC coefficients if only GCPs of urban areas are used (without GCPs, see
Figure 8 and
Figure 11).
The number of extracted GCPs with the proposed method mostly depends on the quantity of roads on the target images. Good results are obtained with all types of roads and different land covers. The proposed method extracts more than 90 points per image in average (while the previous method substantially less), and the density of GCPs that are inside the city perimeter is higher than outside. The points that were obtained by the proposed method are evenly distributed and achieve a higher accuracy when using only city points. In this case, the RMSEs at manually measured ICPs are slightly higher, which can also be attributed to the distribution of these points. As the GCPs are confined to the built area, the errors at ICPs outside the city area are slightly bigger. For this reason, it can be concluded that the extraction of GCPs is feasible and also quite accurate in densely built areas.
Another important aspect of the proposed extraction algorithm is its robustness towards different imaging conditions. It is capable of efficiently detecting GCPs on VHR panchromatic images of different dates and different off-nadir angles. From the results, is impossible to tell which image has high off-nadir angles, longest shadows or from which side of the imaged area the images were taken. As the algorithm tries to detect GCPs on all computed crossroads, it is easier to obtain points in built areas where the roads are abundant, although the road detection is often not optimal (mainly because of shadows and occlusions). This algorithm capability makes it even more suitable for the orthorectification of images that mostly cover urban areas.
After the geometric corrections, the RMSEs at the GCPs and ICPs are generally in the same range, independent of the number of GCPs that are used in the model refinement. Due to the random errors, higher RMSEs were expected when sets with higher number of GCPs are employed. As this is not the case it can be concluded that the random errors are very small and they are additionally minimized during the refinement. The set size has a bigger impact on the refinement methods. The offset correction performs slightly better when less than 30 GCPs are used for Pléiades imagery. Therefore, the marginally worse results when using small sets can also be attributed to the refinement method. Nevertheless, the difference is small and it is not the main reason for high RMSEs that were obtained with the previous method when using only city GCPs. The refinement method is sensor specific and it should be taken into account in geometric correction algorithms.
The proposed method performs well in either rural or urban areas. Rural areas usually exhibit a network of narrower roads that are less occluded by buildings. In such scenario, the extraction of GCPs is straightforward and it results in many points (with good atmospheric conditions) even if the previous method is used. Problems may occur when non-urban areas only feature wide roads (e.g., highways) or big intersections. In such case, the proposed method has a higher chance of extracting accurate GCPs. On the other hand, the road network is always dense in urban areas, which enables the possibility of a high number of GCP candidates. The drawback of urban areas is mostly the occlusions that are mainly created by high buildings, trees, and moving objects (e.g., cars, public transport), and other impervious areas that are similar to roads and hinder the road detection. The urban roads are generally wider than in rural areas, which contributes to a higher accuracy and number of GCPs obtained by the proposed method.
It would be reasonable to differentiate the algorithms according to the type of land cover, using the proposed algorithms only on the urban areas, and the previous one on the rest of the image, as the previous method has smaller computational cost. However, the performance of the road detection and GCP extraction is only marginally dependant on the type of land cover and mostly depends on the type of roads present in the image. Additionally, it would need to classify the raw image to urban–non-urban area before the road detection, which would need supplementary procedures and more processing time. Only applying the proposed method that generates accurate GCPs from all types of roads seems to be a more straightforward solution that does not substantially affect the total computational cost, especially if enough hardware resources are available. Nevertheless, the division of the image to land cover types would also benefit the proposed road detection method, as different (suitable) parameters could be set for the image segmentation and classification for each land cover.
The potential of the proposed method is demonstrated for regions in Slovenia, where accurate reference data is available. However, the method can work also in other parts of the world. Currently, OpenStreetMap road layers are implemented in the processing and they are globally available. Although their accuracy is questionable, they can still be used as a supporting layer or when more accurate data is not available. The images of regions where national reference data is accessible can be easily processed after such data is added in the database. Areas without any roads cannot benefit from the proposed method. In this case, the image of such areas can only be automatically processed without GCPs.
The presented results clearly showed the potential of the method for a robust geometric correction of panchromatic images with very-high resolution. The proposed method shows a good performance on images with complex land cover, which is mostly characterized by densely populated urban areas with high buildings. Although a diverse set of images is used, a more extensive VHR images dataset (different sensors and even higher resolutions) would be necessary to additionally test the robustness in regard to different resolutions and sensors, and to improve the processing parameters of the method. It is still mandatory to test the performance of the algorithm where non-ideal atmospheric conditions are present (e.g., clouds or/and haze) or during more extreme landscape conditions (e.g., snow cover).
6. Conclusions
An improved automatic workflow for generating VHR satellite orthoimages is proposed in this study. The procedure works with level 1 or level 2 images and it employs an automatic GCPs extraction procedure that is based on the multi-step matching of road network features that are derived from the input satellite image and reference data. In contrast to the previously implemented road extraction method, we utilize a fast segmentation-based method that includes a simple decision tree classification. The proposed method is focused on images that contain dense urban areas, where the extraction of road features is very challenging. To achieve a high density of extracted GCPs, it concentrates on predefined crossroads that are in urban environments present in high numbers. Thus, some GCPs are common to all images of the same area and they can therefore be used for a joint adjustment of a block of images.
The performance of the processing procedure is tested on 14 Pléiades panchromatic images of two highly urban regions in Slovenia. The accuracy tests demonstrate the capability of the proposed procedure to achieve root mean square errors of approximately one pixel or even the sub-pixel level. The procedure is robust and also accurate for images of high off-nadir angles and various acquisition dates. Furthermore, the proposed extraction algorithm can retrieve a high number of very accurate GCPs, also in city areas with relatively high buildings that may occlude the road network themselves or indirectly (by their shadows).
The developed procedure is currently functional with Pléiades imagery, but the testing of images of even higher resolution (e.g., WorldView satellite series) is in progress. Besides the basic aim of generating orthoimages, the procedure is also designed to support the creation of satellite true orthoimages—i.e., orthoimages where distortions due to high objects (e.g., high buildings) are also minimized. Although the development of this final stage is not yet completed, the first results are very promising.