A Mixed Model Approach to Vegetation Condition Prediction Using Artificial Neural Networks (ANN): Case of Kenya’s Operational Drought Monitoring
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Modelling Scheme
2.2.1. Pre-Modelling
2.2.2. Model Building
- A statistical approach–generalized additive models (GAM), and
- Artificial neural networks (ANN).
General Additive Models
Artificial Neural Networks (ANN)
2.2.3. Model Evaluation
3. Results and Discussion
3.1. Analysis of Past Drought Events
3.2. GAM Model Results
3.3. Artificial Neural Network Model Results
3.3.1. Artificial Neural Network Performance in Training and Validation
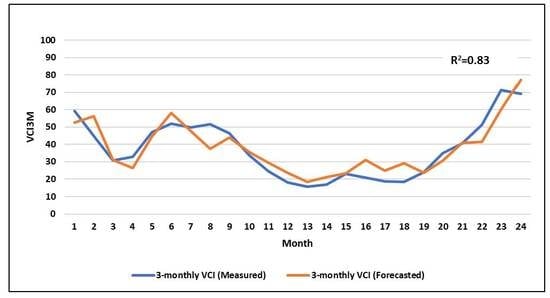
3.3.2. Performance of the Best ANN Model in the Test Dataset
3.4. Validation of the Key Assumption of the Study
3.4.1. Appropriateness of the Use of GAM
3.4.2. Investigation of Multi-Collinearity
3.4.3. Performance of Models with Lags of the Same Variable
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A1. GAM Model Performance by Lag Time

| Statistic | Lag1 | Lag2 | Lag3 |
|---|---|---|---|
| Mean | 0.62 | 0.44 | 0.25 |
| Median | 0.78 | 0.49 | 0.27 |
| Range | 0.76 | 0.47 | 0.24 |
| Minimum | 0.09 | 0.13 | 0.09 |
| Maximum | 0.85 | 0.61 | 0.33 |
Appendix A2. ANN Model Performance by Lag Time

| Statistic | Lag 1 | Lag 2 | Lag 3 |
|---|---|---|---|
| Mean | 0.60 | 0.36 | 0.15 |
| Median | 0.76 | 0.38 | 0.15 |
| Range | 0.76 | 0.40 | 0.22 |
| Minimum | 0.07 | 0.11 | 0.03 |
| Maximum | 0.83 | 0.51 | 0.25 |
Appendix B
| No | Model | R2 Training | R2 Validation | Overfit Index | Overfit | Lag Time |
|---|---|---|---|---|---|---|
| 1 | VCIDekad_lag1+SPI1M_lag1 | 0.86 | 0.85 | 0.01 | No | Lag1 |
| 2 | VCIDekad_lag1+SPI3M_lag1 | 0.86 | 0.85 | 0.01 | No | Lag1 |
| 3 | VCIDekad_lag1+RFE1M_lag1 | 0.85 | 0.85 | 0.01 | No | Lag1 |
| 4 | VCI1M_lag1+SPI3M_lag1 | 0.85 | 0.84 | 0.01 | No | Lag1 |
| 5 | VCI1M_lag1+SPI1M_lag1 | 0.85 | 0.84 | 0.01 | No | Lag1 |
| 6 | VCI1M_lag1+RFE1M_lag1 | 0.85 | 0.84 | 0.01 | No | Lag1 |
| 7 | VCIDekad_lag1+RCI1M_lag1 | 0.85 | 0.84 | 0.01 | No | Lag1 |
| 8 | VCI1M_lag1+RCI1M_lag1 | 0.84 | 0.83 | 0.01 | No | Lag1 |
| 9 | VCIDekad_lag1+RCI3M_lag1 | 0.84 | 0.83 | 0.01 | No | Lag1 |
| 10 | VCIDekad_lag1+RFE3M_lag1 | 0.84 | 0.83 | 0.01 | No | Lag1 |
| 11 | VCI1M_lag1+RCI3M_lag1 | 0.84 | 0.83 | 0.01 | No | Lag1 |
| 12 | VCI1M_lag1+RFE3M_lag1 | 0.83 | 0.83 | 0.01 | No | Lag1 |
| 13 | VCI3M_lag1+SPI3M_lag1 | 0.82 | 0.82 | 0.01 | No | Lag1 |
| 14 | VCIDekad_lag1 | 0.81 | 0.8 | 0.01 | No | Lag1 |
| 15 | VCI3M_lag1+RCI3M_lag1 | 0.81 | 0.8 | 0.01 | No | Lag1 |
| 16 | VCI1M_lag1 | 0.81 | 0.8 | 0.01 | No | Lag1 |
| 17 | VCI3M_lag1+SPI1M_lag1 | 0.81 | 0.79 | 0.01 | No | Lag1 |
| 18 | VCI3M_lag1+RCI1M_lag1 | 0.78 | 0.77 | 0.01 | No | Lag1 |
| 19 | VCI3M_lag1+RFE3M_lag1 | 0.78 | 0.77 | 0.01 | No | Lag1 |
| 20 | VCI3M_lag1+RFE1M_lag1 | 0.78 | 0.76 | 0.01 | No | Lag1 |
| 21 | VCI3M_lag1 | 0.72 | 0.69 | 0.02 | No | Lag1 |
| 22 | VCIDekad_lag2+SPI1M_lag2 | 0.61 | 0.61 | 0 | No | Lag2 |
| 23 | VCI1M_lag2+SPI1M_lag2 | 0.6 | 0.6 | 0 | No | Lag2 |
| 24 | VCIDekad_lag2+RFE1M_lag2 | 0.58 | 0.58 | 0 | No | Lag2 |
| 25 | VCI1M_lag2+RFE1M_lag2 | 0.58 | 0.57 | 0 | No | Lag2 |
| 26 | VCI1M_lag2+SPI3M_lag2 | 0.57 | 0.56 | 0.01 | No | Lag2 |
| 27 | VCIDekad_lag2+SPI3M_lag2 | 0.57 | 0.56 | 0.01 | No | Lag2 |
| 28 | VCI3M_lag2+SPI1M_lag2 | 0.56 | 0.56 | 0 | No | Lag2 |
| 29 | VCIDekad_lag2+RCI1M_lag2 | 0.56 | 0.55 | 0.02 | No | Lag2 |
| 30 | VCI3M_lag2+SPI3M_lag2 | 0.55 | 0.55 | 0 | No | Lag2 |
| 31 | VCI1M_lag2+RCI1M_lag2 | 0.56 | 0.55 | 0.02 | No | Lag2 |
| 32 | NDVIDekad_lag1+SPI3M_lag1 | 0.56 | 0.54 | 0.02 | No | Lag1 |
| 33 | VCIDekad_lag2+RCI3M_lag2 | 0.55 | 0.54 | 0.02 | No | Lag2 |
| 34 | VCI1M_lag2+RCI3M_lag2 | 0.55 | 0.54 | 0.02 | No | Lag2 |
| 35 | VCI3M_lag2+RCI3M_lag2 | 0.53 | 0.51 | 0.01 | No | Lag2 |
| 36 | NDVIDekad_lag2+SPI3M_lag2 | 0.52 | 0.51 | 0.01 | No | Lag2 |
| 37 | VCI3M_lag2+RCI1M_lag2 | 0.51 | 0.49 | 0.02 | No | Lag2 |
| 38 | VCI3M_lag2+RFE1M_lag2 | 0.5 | 0.49 | 0.01 | No | Lag2 |
| 39 | NDVIDekad_lag1+RCI3M_lag1 | 0.51 | 0.49 | 0.02 | No | Lag1 |
| 40 | VCI1M_lag2+RFE3M_lag2 | 0.51 | 0.49 | 0.02 | No | Lag2 |
| 41 | VCIDekad_lag2+RFE3M_lag2 | 0.51 | 0.49 | 0.02 | No | Lag2 |
| 42 | SPI3M_lag2 | 0.49 | 0.49 | 0 | No | Lag2 |
| 43 | SPI3M_lag1 | 0.5 | 0.48 | 0.02 | No | Lag1 |
| 44 | NDVIDekad_lag2+RCI3M_lag2 | 0.48 | 0.46 | 0.02 | No | Lag2 |
| 45 | VCI3M_lag2+RFE3M_lag2 | 0.44 | 0.43 | 0.02 | No | Lag2 |
| 46 | RCI3M_lag2 | 0.42 | 0.41 | 0.01 | No | Lag2 |
| 47 | VCI1M_lag2 | 0.43 | 0.4 | 0.03 | No | Lag2 |
| 48 | VCIDekad_lag2 | 0.43 | 0.4 | 0.03 | No | Lag2 |
| 49 | NDVIDekad_lag1+RFE3M_lag1 | 0.41 | 0.39 | 0.02 | No | Lag1 |
| 50 | RCI3M_lag1 | 0.41 | 0.39 | 0.02 | No | Lag1 |
| 51 | NDVIDekad_lag2+SPI1M_lag2 | 0.4 | 0.37 | 0.03 | No | Lag2 |
| 52 | VCIDekad_lag3+SPI1M_lag3 | 0.35 | 0.33 | 0.01 | No | Lag3 |
| 53 | VCI1M_lag3+SPI1M_lag3 | 0.34 | 0.33 | 0.01 | No | Lag3 |
| 54 | NDVIDekad_lag2+RFE3M_lag2 | 0.35 | 0.33 | 0.02 | No | Lag2 |
| 55 | VCI3M_lag3+SPI1M_lag3 | 0.33 | 0.32 | 0.01 | No | Lag3 |
| 56 | VCI3M_lag2 | 0.33 | 0.31 | 0.02 | No | Lag2 |
| 57 | RFE3M_lag1 | 0.32 | 0.31 | 0.01 | No | Lag1 |
| 58 | NDVIDekad_lag3+SPI3M_lag3 | 0.33 | 0.31 | 0.02 | No | Lag3 |
| 59* | NDVIDekad_lag2+RCI1M_lag2 | 0.35 | 0.31 | 0.05 | Yes | Lag2 |
| 60 | VCI1M_lag3+SPI3M_lag3 | 0.32 | 0.31 | 0.02 | No | Lag3 |
| 61 | VCI3M_lag3+SPI3M_lag3 | 0.32 | 0.31 | 0.01 | No | Lag3 |
| 62 | VCIDekad_lag3+SPI3M_lag3 | 0.32 | 0.31 | 0.01 | No | Lag3 |
| 63 | NDVIDekad_lag2+RFE1M_lag2 | 0.34 | 0.31 | 0.03 | No | Lag2 |
| 64 | SPI3M_lag3 | 0.31 | 0.3 | 0.02 | No | Lag3 |
| 65 | SPI1M_lag2 | 0.32 | 0.29 | 0.03 | No | Lag2 |
| 66 | NDVIDekad_lag3+RCI3M_lag3 | 0.31 | 0.29 | 0.02 | No | Lag3 |
| 67 | NDVIDekad_lag1+SPI1M_lag1 | 0.31 | 0.29 | 0.03 | No | Lag1 |
| 68 | VCI1M_lag3+RCI3M_lag3 | 0.3 | 0.28 | 0.02 | No | Lag3 |
| 69 | VCI3M_lag3+RCI3M_lag3 | 0.3 | 0.28 | 0.02 | No | Lag3 |
| 70 | VCIDekad_lag3+RCI3M_lag3 | 0.3 | 0.28 | 0.02 | No | Lag3 |
| 71 | RFE3M_lag2 | 0.29 | 0.28 | 0.01 | No | Lag2 |
| 72 | VCIDekad_lag3+RFE1M_lag3 | 0.31 | 0.28 | 0.03 | No | Lag3 |
| 73 | VCI1M_lag3+RFE1M_lag3 | 0.31 | 0.28 | 0.03 | No | Lag3 |
| 74 | NDVIDekad_lag3+SPI1M_lag3 | 0.3 | 0.28 | 0.02 | No | Lag3 |
| 75 | VCIDekad_lag3+RCI1M_lag3 | 0.29 | 0.27 | 0.02 | No | Lag3 |
| 76 | VCI1M_lag3+RCI1M_lag3 | 0.29 | 0.27 | 0.02 | No | Lag3 |
| 77 | VCI3M_lag3+RFE1M_lag3 | 0.3 | 0.27 | 0.03 | No | Lag3 |
| 78 | VCI3M_lag3+RCI1M_lag3 | 0.28 | 0.26 | 0.02 | No | Lag3 |
| 79 | RCI3M_lag3 | 0.28 | 0.26 | 0.02 | No | Lag3 |
| 80 | NDVIDekad_lag1+RCI1M_lag1 | 0.28 | 0.26 | 0.02 | No | Lag1 |
| 81 | VCIDekad_lag3+RFE3M_lag3 | 0.25 | 0.24 | 0.01 | No | Lag3 |
| 82 | VCI1M_lag3+RFE3M_lag3 | 0.25 | 0.23 | 0.01 | No | Lag3 |
| 83 | NDVIDekad_lag1+RFE1M_lag1 | 0.26 | 0.23 | 0.02 | No | Lag1 |
| 84 | SPI1M_lag3 | 0.25 | 0.23 | 0.02 | No | Lag3 |
| 85 | VCI3M_lag3+RFE3M_lag3 | 0.24 | 0.23 | 0.02 | No | Lag3 |
| 86 | NDVIDekad_lag3+RCI1M_lag3 | 0.24 | 0.22 | 0.02 | No | Lag3 |
| 87* | RCI1M_lag2 | 0.25 | 0.21 | 0.04 | Yes | Lag2 |
| 88 | RFE1M_lag2 | 0.24 | 0.21 | 0.03 | No | Lag2 |
| 89 | NDVIDekad_lag3+RFE1M_lag3 | 0.24 | 0.21 | 0.03 | No | Lag3 |
| 90 | NDVIDekad_lag3+RFE3M_lag3 | 0.23 | 0.2 | 0.02 | No | Lag3 |
| 91 | RFE3M_lag3 | 0.21 | 0.19 | 0.02 | No | Lag3 |
| 92 | NDVIDekad_lag1 | 0.22 | 0.19 | 0.03 | No | Lag1 |
| 93 | VCI1M_lag3 | 0.19 | 0.18 | 0.01 | No | Lag3 |
| 94 | VCIDekad_lag3 | 0.19 | 0.18 | 0.01 | No | Lag3 |
| 95 | RCI1M_lag3 | 0.19 | 0.17 | 0.02 | No | Lag3 |
| 96 | RFE1M_lag3 | 0.2 | 0.17 | 0.03 | No | Lag3 |
| 97 | SPI1M_lag1 | 0.17 | 0.15 | 0.03 | No | Lag1 |
| 98 | VCI3M_lag3 | 0.15 | 0.13 | 0.02 | No | Lag3 |
| 99 | NDVIDekad_lag2 | 0.16 | 0.13 | 0.03 | No | Lag2 |
| 100 | RCI1M_lag1 | 0.13 | 0.12 | 0.01 | No | Lag1 |
| 101 | RFE1M_lag1 | 0.11 | 0.09 | 0.02 | No | Lag1 |
| 102 | NDVIDekad_lag3 | 0.11 | 0.09 | 0.02 | No | Lag3 |
| No | Model | R2 Training | R2 Validation | Overfit Index | Overfit | Lag Time |
|---|---|---|---|---|---|---|
| 1 | VCIDekad_lag1+RFE1M_lag1 | 0.84 | 0.83 | 0.01 | No | 1 |
| 2 | VCI1M_lag1+RFE1M_lag1 | 0.84 | 0.83 | 0.01 | No | 1 |
| 3 | VCIDekad_lag1+SPI1M_lag1 | 0.84 | 0.82 | 0.02 | No | 1 |
| 4 | VCIDekad_lag1+SPI3M_lag1 | 0.84 | 0.82 | 0.02 | No | 1 |
| 5 | VCIDekad_lag1+RCI3M_lag1 | 0.84 | 0.82 | 0.02 | No | 1 |
| 6 | VCI1M_lag1+SPI3M_lag1 | 0.84 | 0.82 | 0.02 | No | 1 |
| 7 | VCI1M_lag1+RCI3M_lag1 | 0.84 | 0.82 | 0.02 | No | 1 |
| 8 | VCI1M_lag1+SPI1M_lag1 | 0.84 | 0.82 | 0.02 | No | 1 |
| 9 | VCIDekad_lag1+RCI1M_lag1 | 0.82 | 0.81 | 0.02 | No | 1 |
| 10 | VCI1M_lag1+RCI1M_lag1 | 0.82 | 0.80 | 0.02 | No | 1 |
| 11 | VCIDekad_lag1+RFE3M_lag1 | 0.82 | 0.80 | 0.02 | No | 1 |
| 12 | VCI1M_lag1+RFE3M_lag1 | 0.81 | 0.79 | 0.02 | No | 1 |
| 13 | VCIDekad_lag1 | 0.79 | 0.78 | 0.01 | No | 1 |
| 14 | VCI1M_lag1 | 0.78 | 0.77 | 0.01 | No | 1 |
| 15 | VCI3M_lag1+SPI3M_lag1 | 0.79 | 0.77 | 0.03 | No | 1 |
| 16 | VCI3M_lag1+RFE1M_lag1 | 0.77 | 0.77 | 0.01 | No | 1 |
| 17 | VCI3M_lag1+RCI3M_lag1 | 0.79 | 0.76 | 0.03 | No | 1 |
| 18 | VCI3M_lag1+RCI1M_lag1 | 0.77 | 0.75 | 0.02 | No | 1 |
| 19* | VCI3M_lag1+SPI1M_lag1 | 0.78 | 0.74 | 0.04 | Yes | 1 |
| 20 | VCI3M_lag1+RFE3M_lag1 | 0.74 | 0.72 | 0.02 | No | 1 |
| 21 | VCI3M_lag1 | 0.68 | 0.66 | 0.02 | No | 1 |
| 22* | NDVIDekad_lag1+SPI3M_lag1 | 0.60 | 0.57 | 0.04 | Yes | 1 |
| 23* | NDVIDekad_lag1+RCI3M_lag1 | 0.59 | 0.54 | 0.05 | Yes | 1 |
| 24* | VCI1M_lag2+SPI1M_lag2 | 0.57 | 0.51 | 0.06 | Yes | 2 |
| 25* | VCIDekad_lag2+SPI1M_lag2 | 0.58 | 0.51 | 0.07 | Yes | 2 |
| 26* | VCIDekad_lag2+SPI3M_lag2 | 0.54 | 0.51 | 0.04 | Yes | 2 |
| 27* | VCI1M_lag2+SPI3M_lag2 | 0.56 | 0.49 | 0.07 | Yes | 2 |
| 28* | VCIDekad_lag2+RCI1M_lag2 | 0.53 | 0.47 | 0.06 | Yes | 2 |
| 29* | VCIDekad_lag2+RFE1M_lag2 | 0.52 | 0.47 | 0.06 | Yes | 2 |
| 30* | VCI1M_lag2+RCI1M_lag2 | 0.53 | 0.46 | 0.07 | Yes | 2 |
| 31* | VCI1M_lag2+RCI3M_lag2 | 0.53 | 0.46 | 0.08 | Yes | 2 |
| 32* | VCI1M_lag2+RFE1M_lag2 | 0.53 | 0.46 | 0.07 | Yes | 2 |
| 33* | VCIDekad_lag2+RCI3M_lag2 | 0.52 | 0.45 | 0.07 | Yes | 2 |
| 34* | VCI3M_lag2+SPI3M_lag2 | 0.52 | 0.44 | 0.08 | Yes | 2 |
| 35* | VCI3M_lag2+SPI1M_lag2 | 0.50 | 0.44 | 0.06 | Yes | 2 |
| 36* | SPI3M_lag1 | 0.47 | 0.43 | 0.03 | Yes | 1 |
| 37* | NDVIDekad_lag2+SPI3M_lag2 | 0.48 | 0.43 | 0.05 | Yes | 2 |
| 38 | SPI3M_lag2 | 0.42 | 0.42 | 0.00 | No | 2 |
| 39* | VCI3M_lag2+RCI3M_lag2 | 0.49 | 0.40 | 0.09 | Yes | 2 |
| 40* | NDVIDekad_lag2+RCI3M_lag2 | 0.45 | 0.40 | 0.05 | Yes | 2 |
| 41* | VCI3M_lag2+RCI1M_lag2 | 0.51 | 0.39 | 0.12 | Yes | 2 |
| 42* | RCI3M_lag1 | 0.43 | 0.39 | 0.04 | Yes | 1 |
| 43* | VCI3M_lag2+RFE1M_lag2 | 0.47 | 0.38 | 0.09 | Yes | 2 |
| 44* | NDVIDekad_lag1+RFE3M_lag1 | 0.47 | 0.37 | 0.09 | Yes | 1 |
| 45* | VCIDekad_lag2+RFE3M_lag2 | 0.46 | 0.37 | 0.09 | Yes | 2 |
| 46* | VCI1M_lag2+RFE3M_lag2 | 0.46 | 0.37 | 0.09 | Yes | 2 |
| 47 | RCI3M_lag2 | 0.38 | 0.37 | 0.01 | No | 2 |
| 48* | NDVIDekad_lag1+SPI1M_lag1 | 0.43 | 0.36 | 0.06 | Yes | 1 |
| 49* | VCI1M_lag2 | 0.39 | 0.36 | 0.03 | Yes | 2 |
| 50* | VCIDekad_lag2 | 0.39 | 0.36 | 0.03 | Yes | 2 |
| 51* | NDVIDekad_lag2+SPI1M_lag2 | 0.39 | 0.32 | 0.07 | Yes | 2 |
| 52* | NDVIDekad_lag1+RCI1M_lag1 | 0.35 | 0.32 | 0.03 | Yes | 1 |
| 53* | VCI3M_lag2+RFE3M_lag2 | 0.41 | 0.29 | 0.12 | Yes | 2 |
| 54 | NDVIDekad_lag1 | 0.28 | 0.27 | 0.01 | No | 1 |
| 55 | RFE3M_lag1 | 0.27 | 0.26 | 0.01 | No | 1 |
| 56* | NDVIDekad_lag1+RFE1M_lag1 | 0.34 | 0.26 | 0.08 | Yes | 1 |
| 57* | VCIDekad_lag3+SPI1M_lag3 | 0.31 | 0.25 | 0.06 | Yes | 3 |
| 58 | SPI1M_lag2 | 0.26 | 0.24 | 0.02 | No | 2 |
| 59* | VCI3M_lag2 | 0.28 | 0.23 | 0.05 | Yes | 2 |
| 60* | VCIDekad_lag3+SPI3M_lag3 | 0.30 | 0.23 | 0.07 | Yes | 3 |
| 61* | VCI1M_lag3+SPI1M_lag3 | 0.31 | 0.23 | 0.08 | Yes | 3 |
| 62* | VCI1M_lag3+SPI3M_lag3 | 0.31 | 0.23 | 0.08 | Yes | 3 |
| 63* | NDVIDekad_lag2+RCI1M_lag2 | 0.31 | 0.23 | 0.09 | Yes | 2 |
| 64* | VCI3M_lag3+SPI3M_lag3 | 0.28 | 0.23 | 0.06 | Yes | 3 |
| 65* | NDVIDekad_lag2+RFE3M_lag2 | 0.31 | 0.22 | 0.10 | Yes | 2 |
| 66 | SPI3M_lag3 | 0.23 | 0.22 | 0.01 | No | 3 |
| 67* | NDVIDekad_lag3+SPI3M_lag3 | 0.27 | 0.21 | 0.06 | Yes | 3 |
| 68* | VCI3M_lag3+SPI1M_lag3 | 0.32 | 0.20 | 0.12 | Yes | 3 |
| 69 | RCI1M_lag2 | 0.20 | 0.19 | 0.01 | No | 2 |
| 70* | NDVIDekad_lag2+RFE1M_lag2 | 0.24 | 0.19 | 0.05 | Yes | 2 |
| 71* | RFE3M_lag2 | 0.23 | 0.19 | 0.05 | Yes | 2 |
| 72* | NDVIDekad_lag3+RCI3M_lag3 | 0.27 | 0.18 | 0.09 | Yes | 3 |
| 73 | SPI1M_lag3 | 0.20 | 0.18 | 0.02 | No | 3 |
| 74* | NDVIDekad_lag3+SPI1M_lag3 | 0.27 | 0.17 | 0.10 | Yes | 3 |
| 75* | VCI1M_lag3+RCI3M_lag3 | 0.25 | 0.17 | 0.08 | Yes | 3 |
| 76* | RCI3M_lag3 | 0.20 | 0.16 | 0.04 | Yes | 3 |
| 77* | VCI3M_lag3+RCI3M_lag3 | 0.27 | 0.16 | 0.11 | Yes | 3 |
| 78* | VCIDekad_lag3+RCI1M_lag3 | 0.27 | 0.16 | 0.11 | Yes | 3 |
| 79* | VCI1M_lag3+RFE1M_lag3 | 0.23 | 0.15 | 0.07 | Yes | 3 |
| 80* | VCI1M_lag3+RFE3M_lag3 | 0.21 | 0.15 | 0.06 | Yes | 3 |
| 81* | VCI3M_lag3+RCI1M_lag3 | 0.30 | 0.14 | 0.15 | Yes | 3 |
| 82* | VCIDekad_lag3+RCI3M_lag3 | 0.27 | 0.14 | 0.12 | Yes | 3 |
| 83* | VCI1M_lag3+RCI1M_lag3 | 0.30 | 0.14 | 0.16 | Yes | 3 |
| 84* | VCIDekad_lag3+RFE1M_lag3 | 0.24 | 0.14 | 0.10 | Yes | 3 |
| 85* | NDVIDekad_lag3+RFE3M_lag3 | 0.19 | 0.13 | 0.06 | Yes | 3 |
| 86 | RFE1M_lag2 | 0.14 | 0.13 | 0.01 | No | 2 |
| 87* | VCI3M_lag3+RFE1M_lag3 | 0.20 | 0.13 | 0.07 | Yes | 3 |
| 88* | VCIDekad_lag3+RFE3M_lag3 | 0.22 | 0.13 | 0.09 | Yes | 3 |
| 89* | VCI3M_lag3+RFE3M_lag3 | 0.19 | 0.12 | 0.07 | Yes | 3 |
| 90 | RFE3M_lag3 | 0.14 | 0.12 | 0.01 | No | 3 |
| 91 | VCIDekad_lag3 | 0.14 | 0.11 | 0.03 | No | 3 |
| 92* | NDVIDekad_lag3+RCI1M_lag3 | 0.18 | 0.11 | 0.07 | Yes | 3 |
| 93 | SPI1M_lag1 | 0.14 | 0.11 | 0.02 | No | 1 |
| 94 | RCI1M_lag1 | 0.11 | 0.11 | (0.00) | No | 1 |
| 95 | NDVIDekad_lag2 | 0.13 | 0.11 | 0.02 | No | 2 |
| 96* | RCI1M_lag3 | 0.13 | 0.10 | 0.03 | Yes | 3 |
| 97* | VCI1M_lag3 | 0.15 | 0.10 | 0.05 | Yes | 3 |
| 98 | VCI3M_lag3 | 0.09 | 0.07 | 0.02 | No | 3 |
| 99 | RFE1M_lag1 | 0.07 | 0.07 | (0.00) | No | 1 |
| 100* | NDVIDekad_lag3+RFE1M_lag3 | 0.14 | 0.06 | 0.08 | Yes | 3 |
| 101 | RFE1M_lag3 | 0.08 | 0.06 | 0.02 | No | 3 |
| 102 | NDVIDekad_lag3 | 0.05 | 0.03 | 0.01 | No | 3 |
Appendix C


References
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Bordi, I.; Fraedrich, K.; Petitta, M.; Sutera, A. Methods for predicting drought occurrences. In Proceedings of the 6th International Conference of the European Water Resources Association, Menton, France, 7–10 September 2005; pp. 7–10. [Google Scholar]
- Ali, Z.; Hussain, I.; Faisal, M.; Nazir, H.M.; Hussain, T.; Shad, M.Y.; Mohamd Shoukry, A.; Hussain Gani, S. Forecasting Drought Using Multilayer Perceptron Artificial Neural Network Model. Adv. Meteorol. 2017, 2017, 5681308. [Google Scholar] [CrossRef]
- UNOOSA. Data Application of the Month: Drought Monitoring. UN-SPIDER. 2015. Available online: http://www.un-spider.org/links-and-resources/data-sources/daotm-drought (accessed on 11 November 2017).
- Government of Kenya. Kenya Post-Disaster Needs Assessment: 2008–2011 Drought. 2012. Available online: http://www.gfdrr.org/sites/gfdrr/files/Kenya_PDNA_Final.pdf (accessed on 9 November 2018).
- Cody, B.A.; Folger, P.; Brougher, C. California Drought: Hydrological and Regulatory Water Supply Issues; Congressional Research Service: Washington, DC, USA, 2010. [Google Scholar]
- Udmale, P.D.; Ichikawa, Y.; Manandhar, S.; Ishidaira, H.; Kiem, A.S.; Shaowei, N.; Panda, S.N. How did the 2012 drought affect rural livelihoods in vulnerable areas? Empirical evidence from India. Int. J. Disaster Risk Reduct. 2015, 13, 454–469. [Google Scholar] [CrossRef]
- Ding, Y.; Hayes, M.J.; Widhalm, M. Measuring economic impacts of drought: A review and discussion. Disaster Prev. Manag. Int. J. 2011, 20, 434–446. [Google Scholar] [CrossRef]
- Mariotti, A.; Schubert, S.; Mo, K.; Peters-Lidard, C.; Wood, A.; Pulwarty, R.; Huang, J.; Barrie, D. Advancing drought understanding, monitoring, and prediction. Bull. Am. Meteorol. Soc. 2013, 94, ES186–ES188. [Google Scholar] [CrossRef]
- Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using low resolution satellite imagery for yield prediction and yield anomaly detection. Remote Sens. 2013, 5, 1704–1733. [Google Scholar] [CrossRef]
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef]
- Meroni, M.; Verstraete, M.M.; Rembold, F.; Urbano, F.; Kayitakire, F. A phenology-based method to derive biomass production anomalies for food security monitoring in the Horn of Africa. Int. J. Remote Sens. 2014, 35, 2472–2492. [Google Scholar] [CrossRef]
- Du, L.; Tian, Q.; Yu, T.; Meng, Q.; Jancso, T.; Udvardy, P.; Huang, Y. A comprehensive drought monitoring method integrating MODIS and TRMM data. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 245–253. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology; American Meteorological Society: Boston, MA, USA, 1993; Volume 17, pp. 179–183. [Google Scholar]
- Palmer, W.C. Keeping track of crop moisture conditions, nationwide: The new crop moisture index. Weatherwise 1968, 21, 156–161. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Huang, Y.F.; Ang, J.T.; Tiong, Y.J.; Mirzaei, M.; Amin, M.Z.M. Drought Forecasting using SPI and EDI under RCP-8.5 Climate Change Scenarios for Langat River Basin, Malaysia. Procedia Eng. 2016, 154, 710–717. [Google Scholar] [CrossRef]
- Khadr, M. Forecasting of meteorological drought using hidden Markov model (case study: The upper Blue Nile river basin, Ethiopia). Ain Shams Eng. J. 2016, 7, 47–56. [Google Scholar] [CrossRef]
- Wichitarapongsakun, P.; Sarin, C.; Klomjek, P.; Chuenchooklin, S. Rainfall prediction and meteorological drought analysis in the Sakae Krang River basin of Thailand. Agric. Nat. Resour. 2016, 50, 490–498. [Google Scholar] [CrossRef]
- Svoboda, M.; LeComte, D.; Hayes, M.; Heim, R.; Gleason, K.; Angel, J.; Rippey, B.; Tinker, R.; Palecki, M.; Stooksbury, D.; et al. The drought monitor. Bull. Am. Meteorol. Soc. 2002, 83, 1181–1190. [Google Scholar] [CrossRef]
- Klisch, A.; Atzberger, C. Operational drought monitoring in Kenya using MODIS NDVI time series. Remote Sens. 2016, 8, 267. [Google Scholar] [CrossRef]
- Beesley, J. The Hunger Safety Nets Programme in Kenya: A Social Protection Case Study; Oxfam Publishing: Oxford, UK, 2011. [Google Scholar]
- Brown, J.; Howard, D.; Wylie, B.; Frieze, A.; Ji, L.; Gacke, C. Application-ready expedited MODIS data for operational land surface monitoring of vegetation condition. Remote Sens. 2015, 7, 16226–16240. [Google Scholar] [CrossRef]
- Hayes, M.J.; Svoboda, M.D.; Wilhite, D.A.; Vanyarkho, O.V. Monitoring the 1996 drought using the standardized precipitation index. Bull. Am. Meteorol. Soc. 1999, 80, 429–438. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Nakhjiri, N. A near real-time satellite-based global drought climate data record. Environ. Res. Lett. 2012, 7, 044037. [Google Scholar] [CrossRef]
- ICPAC. IGAD Climate Prediction and Applications Centre Monthly Climate Bulletin, Climate Review for January 2019 and Forecasts for March 2019. February 2019. Available online: http://www.icpac.net/index.php/component/osdownloads/routedownload/climate/dekadal/dekad-2019/monthly-bulletin-2019/february-2019-bulletin.html?Itemid=622 (accessed on 31 March 2019).
- Yuan, X.; Zhang, M.; Wang, L.; Zhou, T. Understanding and seasonal forecasting of hydrological drought in the Anthropocene. Hydrol. Earth Syst. Sci. 2017, 21, 5477–5492. [Google Scholar] [CrossRef]
- Le, M.H.; Perez, G.C.; Solomatine, D.; Nguyen, L.B. Meteorological Drought Forecasting Based on Climate Signals Using Artificial Neural Network—A Case Study in Khanhhoa Province Vietnam. Procedia Eng. 2016, 154, 1169–1175. [Google Scholar] [CrossRef]
- Maca, P.; Pech, P. Forecasting SPEI and SPI drought indices using the integrated artificial neural networks. Comput. Intell. Neurosci. 2016, 2016, 14. [Google Scholar] [CrossRef]
- AghaKouchak, A. A multivariate approach for persistence-based drought prediction: Application to the 2010–2011 East Africa drought. J. Hydrol. 2015, 526, 127–135. [Google Scholar] [CrossRef]
- Shah, H.; Rane, V.; Nainani, J.; Jeyakumar, B.; Giri, N. Drought Prediction and Management using Big Data Analytics. Int. J. Comput. Appl. 2017, 162, 27–30. [Google Scholar] [CrossRef]
- Enenkel, M.; Steiner, C.; Mistelbauer, T.; Dorigo, W.; Wagner, W.; See, L.; Atzberger, C.; Schneider, S.; Rogenhofer, E. A combined satellite-derived drought indicator to support humanitarian aid organizations. Remote Sens. 2016, 8, 340. [Google Scholar] [CrossRef]
- Tadesse, T.; Demisse, G.B.; Zaitchik, B.; Dinku, T. Satellite-based hybrid drought monitoring tool for prediction of vegetation condition in Eastern Africa: A case study for Ethiopia. Water Resour. Res. 2014, 50, 2176–2190. [Google Scholar] [CrossRef]
- Tadesse, T.; Wardlow, B.D.; Hayes, M.J.; Svoboda, M.D.; Brown, J.F. The Vegetation Outlook (VegOut): A new method for predicting vegetation seasonal greenness. GISci. Remote Sens. 2010, 47, 25–52. [Google Scholar] [CrossRef]
- Wardlow, B.D.; Tadesse, T.; Brown, J.F.; Callahan, K.; Swain, S.; Hunt, E. Vegetation Drought Response Index: An Integration of Satellite, Climate, and Biophysical Data. In Remote Sensing of Drought: Innovative Monitoring Approaches; Wardlow, B.D., Anderson, M.C., Verdin, J.P., Eds.; CPC Press: Boca Raton, FL, USA, 2012; pp. 51–74. [Google Scholar]
- Sedano, F.; Kempeneers, P.; Hurtt, G. A Kalman filter-based method to generate continuous time series of medium-resolution NDVI images. Remote Sens. 2014, 6, 12381–12408. [Google Scholar] [CrossRef]
- Tarnavsky, E.; Grimes, D.; Maidment, R.; Black, E.; Allan, R.P.; Stringer, M.; Chadwick, R.; Kayitakire, F. Extension of the TAMSAT satellite-based rainfall monitoring over Africa and from 1983 to present. J. Appl. Meteorol. Climatol. 2014, 53, 2805–2822. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Standardized Precipitation Index User Guide. 2012. WMO-No. 1090. Available online: http://www.wamis.org/agm/pubs/SPI/WMO_1090_EN.pdf (accessed on 26 April 2019).
- Meroni, M.; Fasbender, D.; Rembold, F.; Atzberger, C.; Klisch, A. Near real-time vegetation anomaly detection with MODIS NDVI: Timeliness vs. accuracy and effect of anomaly computation options. Remote Sens. Environ. 2019, 221, 508–521. [Google Scholar] [CrossRef]
- Atzberger, C.; Carter, M.; Fava, F.; Jensen, N.; Meroni, M.; Mude, A.; Stoeffler, Q.; Vrieling, A. Does the Design Matter? Comparing Satellite-Based Indices for Insuring Pastoralists in Kenya: Technical Report Prepared for the BASIS Assets and Market Access CRSP. 2016. Available online: https://basis.ucdavis.edu/sites/g/files/dgvnsk466/files/2017-05/Cornell_AMA_Technical_Report.pdf (accessed on 19 December 2018).
- Klisch, A.; Atzberger, C.; Luminari, L. Satellite-Based Drought Monitoring In Kenya In An Operational Setting. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-7/W3, 433–439. [Google Scholar] [CrossRef]
- Hastie, T.J. Generalized additive models. In Statistical Models in S; Routledge: Abingdon, UK, 2017; pp. 249–307. [Google Scholar]
- Ramos, E.G.; Martínez, F.V. A Review of Artificial Neural Networks: How Well Do They Perform in Forecasting Time Series? Analítika Revista de Análisis Estadístico 2013, 6, 7–18. [Google Scholar]
- Mitchell, T.M. Machine Learning; WCB: New York City, NY, USA, 1997. [Google Scholar]
- Huang, G.B. Learning capability and storage capacity of two-hidden-layer feedforward networks. IEEE Trans. Neural Netw. 2003, 14, 274–281. [Google Scholar] [CrossRef]
- Hand, D.J.; Till, R.J. A Simple Generalisation of the Area Under the ROC Curve for Multiple Class Classification Problems. Mach. Learn. 2001, 45, 171–186. [Google Scholar] [CrossRef]
















| Variable/Index | Index Calculation | Index Description |
|---|---|---|
| NDVI | NDVI = (NIR−Red)/(NIR+Red) | Predictor variable; sourced from MODIS, the average monthly NDVI quantifying the average monthly vegetation greenness |
| VCI 1 | VCIc,i = 100 × (NDVIc,i-NDVImin c,i)/(NDVImax c,i−NDVImin c,i) [22] | Aggerated over 1- and 3-months period (i = 1,3) for each county (c) in the study areas. The 3-month aggregation of the VCI is predicted variable. |
| RFE | BOKU Rainfall estimate calculated from TAMSAT version 3 product (in mm) [38] | Predictor variable; average monthly rainfall estimate |
| RCI 1 | RCIc,i = 100×(RFEc,i−RFEmin c,i)/(RFEmax c,i−RFEmin c,i) [13] | Predictor variable; RFE values normalized in the 0–1 range (both end points included) for each extent (c) and for each time period (i). |
| SPI | For each location, c and period i, the long-term record of TAMSAT RFE was fitted to a probability distribution then transformed to a normal distribution so that SPImean c,i = 0 [39] | Predictor variable; standardised RFE for each county (c) and for each time period (i = 1,3) |
| Index | Variable Description | 1-Month Lag | 2-Month Lag | 3-Month Lag |
|---|---|---|---|---|
| NDVI_Dekad | NDVI for last dekad of month | ☒ | ☒ | ☒ |
| VCI_Dekad | VCI for the last dekad of month | ☒ | ☒ | ☒ |
| VCI1M | VCI aggregated over 1 month | ☒ | ☒ | ☒ |
| RFE1M | Rainfall Estimate aggregated over 1 month | ☒ | ☒ | ☒ |
| RFE3M | Rainfall Estimate aggregated over the last 3 months | ☒ | ☒ | ☒ |
| SPI1M | Standardised Precipitation Index aggregated over 1 month | ☒ | ☐ | ☒ |
| SPI3M | Standardised Precipitation Index aggregated over the last 3 months | ☒ | ☒ | ☒ |
| RCI1M | Rainfall Condition Index aggregated over 1 month | ☒ | ☒ | ☒ |
| RCI3M | Rainfall Condition Index aggregated over the last 3 months | ☒ | ☒ | ☒ |
| Month 1 | Denotes the month of year | ☐ | ☐ | ☐ |
| VCI3M | VCI aggregated over the last 3 months. The non-lagged value is the dependent variable | ☒ | ☒ | ☒ |
| VCI3M Limit Lower | VCI3M Limit Upper | Description of Class | Drought Class |
|---|---|---|---|
| ≤0 | <10 | Extreme vegetation deficit | 1 |
| 10 | <20 | Severe vegetation deficit | 2 |
| 20 | <35 | Moderate vegetation deficit | 3 |
| 35 | <50 | Normal vegetation conditions | 4 |
| 50 | ≥100 | Above normal vegetation conditions | 5 |
| County | Extreme | Severe | Moderate | Combined |
|---|---|---|---|---|
| Mandera | 8 | 31 | 43 | 82 |
| Marsabit | 8 | 26 | 70 | 104 |
| Turkana | 4 | 28 | 64 | 96 |
| Wajir | 9 | 25 | 61 | 95 |
| Total | 29 | 110 | 238 | 377 |
| No | Model | R2 Training | R2 Validation | Overfit Index | Overfit | Lag Time |
|---|---|---|---|---|---|---|
| 1 | VCIDekad_lag1+SPI1M_lag1 | 0.86 | 0.85 | 0.01 | No | 1 |
| 2 | VCIDekad_lag1+SPI3M_lag1 | 0.86 | 0.85 | 0.01 | No | 1 |
| 3 | VCIDekad_lag1+RFE1M_lag1 | 0.85 | 0.85 | 0.01 | No | 1 |
| 4 | VCI1M_lag1+SPI3M_lag1 | 0.85 | 0.84 | 0.01 | No | 1 |
| 5 | VCI1M_lag1+SPI1M_lag1 | 0.85 | 0.84 | 0.01 | No | 1 |
| 6 | VCI1M_lag1+RFE1M_lag1 | 0.85 | 0.84 | 0.01 | No | 1 |
| 7 | VCIDekad_lag1+RCI1M_lag1 | 0.85 | 0.84 | 0.01 | No | 1 |
| 8 | VCI1M_lag1+RCI1M_lag1 | 0.84 | 0.83 | 0.01 | No | 1 |
| 9 | VCIDekad_lag1+RCI3M_lag1 | 0.84 | 0.83 | 0.01 | No | 1 |
| 10 | VCIDekad_lag1+RFE3M_lag1 | 0.84 | 0.83 | 0.01 | No | 1 |
| 11 | VCI1M_lag1+RCI3M_lag1 | 0.84 | 0.83 | 0.01 | No | 1 |
| 12 | VCI1M_lag1+RFE3M_lag1 | 0.83 | 0.83 | 0.01 | No | 1 |
| 13 | VCI3M_lag1+SPI3M_lag1 | 0.82 | 0.82 | 0.01 | No | 1 |
| 14 | VCIDekad_lag1 | 0.81 | 0.80 | 0.01 | No | 1 |
| 15 | VCI3M_lag1+RCI3M_lag1 | 0.81 | 0.80 | 0.01 | No | 1 |
| 16 | VCI1M_lag1 | 0.81 | 0.80 | 0.01 | No | 1 |
| 17 | VCI3M_lag1+SPI1M_lag1 | 0.81 | 0.79 | 0.01 | No | 1 |
| 18 | VCI3M_lag1+RCI1M_lag1 | 0.78 | 0.77 | 0.01 | No | 1 |
| 19 | VCI3M_lag1+RFE3M_lag1 | 0.78 | 0.77 | 0.01 | No | 1 |
| 20 | VCI3M_lag1+RFE1M_lag1 | 0.78 | 0.76 | 0.01 | No | 1 |
| 211 | VCI3M_lag1 | 0.72 | 0.69 | 0.02 | No | 1 |
| No | Model | Training (R2) | Validation (R2) | Overfit Index | Overfit | ||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | ||||
| 1 | VCIDekad_lag1+RFE1M_lag1 | 0.83 | 0.86 | 0.84 | 0.78 | 0.86 | 0.83 | 0.01 | No |
| 2 | VCI1M_lag1+RFE1M_lag1 | 0.82 | 0.85 | 0.84 | 0.78 | 0.85 | 0.83 | 0.01 | No |
| 3 | VCIDekad_lag1+SPI1M_lag1 | 0.82 | 0.85 | 0.84 | 0.79 | 0.87 | 0.82 | 0.02 | No |
| 4 | VCIDekad_lag1+SPI3M_lag1 | 0.82 | 0.86 | 0.84 | 0.78 | 0.88 | 0.82 | 0.02 | No |
| 5 | VCIDekad_lag1+RCI3M_lag1 | 0.82 | 0.86 | 0.84 | 0.79 | 0.87 | 0.82 | 0.02 | No |
| 6 | VCI1M_lag1+SPI3M_lag1 | 0.81 | 0.85 | 0.84 | 0.78 | 0.87 | 0.82 | 0.02 | No |
| 7 | VCI1M_lag1+RCI3M_lag1 | 0.82 | 0.85 | 0.84 | 0.79 | 0.86 | 0.82 | 0.02 | No |
| 8 | VCI1M_lag1+SPI1M_lag1 | 0.82 | 0.85 | 0.84 | 0.77 | 0.86 | 0.82 | 0.02 | No |
| 9 | VCIDekad_lag1+RCI1M_lag1 | 0.81 | 0.84 | 0.82 | 0.76 | 0.85 | 0.81 | 0.02 | No |
| 10 | VCI1M_lag1+RCI1M_lag1 | 0.80 | 0.84 | 0.82 | 0.75 | 0.84 | 0.80 | 0.02 | No |
| 11 | VCIDekad_lag1+RFE3M_lag1 | 0.79 | 0.84 | 0.82 | 0.75 | 0.83 | 0.80 | 0.02 | No |
| 12 | VCI1M_lag1+RFE3M_lag1 | 0.79 | 0.84 | 0.81 | 0.74 | 0.83 | 0.79 | 0.02 | No |
| 13 | VCIDekad_lag1 | 0.77 | 0.82 | 0.79 | 0.72 | 0.82 | 0.78 | 0.01 | No |
| 14 | VCI1M_lag1 | 0.76 | 0.81 | 0.78 | 0.72 | 0.81 | 0.77 | 0.02 | No |
| 15 | VCI3M_lag1+SPI3M_lag1 | 0.76 | 0.81 | 0.79 | 0.73 | 0.84 | 0.77 | 0.03 | No |
| 16 | VCI3M_lag1+RFE1M_lag1 | 0.76 | 0.79 | 0.77 | 0.72 | 0.80 | 0.77 | 0.01 | No |
| 17 | VCI3M_lag1+RCI3M_lag1 | 0.76 | 0.81 | 0.79 | 0.72 | 0.83 | 0.76 | 0.03 | No |
| 18 | VCI3M_lag1+RCI1M_lag1 | 0.74 | 0.79 | 0.77 | 0.71 | 0.80 | 0.75 | 0.02 | No |
| 19* | VCI3M_lag1+SPI1M_lag1 | 0.73 | 0.80 | 0.78 | 0.70 | 0.82 | 0.74 | 0.04 | Yes |
| 20 | VCI3M_lag1+RFE3M_lag1 | 0.71 | 0.77 | 0.74 | 0.65 | 0.76 | 0.72 | 0.02 | No |
| 21 | VCI3M_lag1 | 0.64 | 0.71 | 0.68 | 0.60 | 0.73 | 0.66 | 0.02 | No |
| Variable | Variable Inflation Factor (VI)F |
|---|---|
| VCI3M_lag1 | 6.14 |
| NDVIDekad_lag1 | 1.41 |
| VCI1M_lag1 | 976.21 |
| VCIDekad_lag1 | 1057.46 |
| RCI1M_lag1 | 4.41 |
| RCI3M_lag1 | 5.90 |
| RFE1M_lag1 | 2.63 |
| RFE3M_lag1 | 2.88 |
| SPI1M_lag1 | 3.34 |
| SPI3M_lag1 | 5.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adede, C.; Oboko, R.; Wagacha, P.W.; Atzberger, C. A Mixed Model Approach to Vegetation Condition Prediction Using Artificial Neural Networks (ANN): Case of Kenya’s Operational Drought Monitoring. Remote Sens. 2019, 11, 1099. https://doi.org/10.3390/rs11091099
Adede C, Oboko R, Wagacha PW, Atzberger C. A Mixed Model Approach to Vegetation Condition Prediction Using Artificial Neural Networks (ANN): Case of Kenya’s Operational Drought Monitoring. Remote Sensing. 2019; 11(9):1099. https://doi.org/10.3390/rs11091099
Chicago/Turabian StyleAdede, Chrisgone, Robert Oboko, Peter Waiganjo Wagacha, and Clement Atzberger. 2019. "A Mixed Model Approach to Vegetation Condition Prediction Using Artificial Neural Networks (ANN): Case of Kenya’s Operational Drought Monitoring" Remote Sensing 11, no. 9: 1099. https://doi.org/10.3390/rs11091099
APA StyleAdede, C., Oboko, R., Wagacha, P. W., & Atzberger, C. (2019). A Mixed Model Approach to Vegetation Condition Prediction Using Artificial Neural Networks (ANN): Case of Kenya’s Operational Drought Monitoring. Remote Sensing, 11(9), 1099. https://doi.org/10.3390/rs11091099