A Geometric Barycenter-Based Clutter Suppression Method for Ship Detection in HF Mixed-Mode Surface Wave Radar

Abstract

The nonhomogeneous clutter is a major challenge for ship detection in high-frequency mixed-mode surface wave radar. In this paper, a geometric barycenter-based reduced-dimension space-time adaptive processing method is proposed to suppress the clutter. Given the measured dataset, the range correlation of sea clutter is first investigated. Then, joint domain localized processing is applied to solve the training samples starve scenario in a practical system. The geometric barycenter-based training data selector is presented to select valid training samples and improve the accuracy of the clutter covariance matrix estimation. Finally, the validity of the proposed method is verified using the experimental data and the results show that it outperforms the conventional method in the nonhomogeneous environment of a practical system.

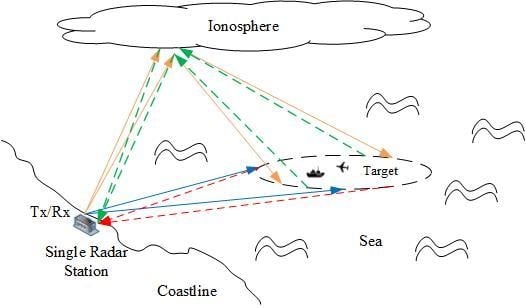
1. Introduction

High-frequency (HF) over-the-horizon radar (OTHR) has been successfully developed for target monitoring and ocean remote sensing by transmitting HF vertical polarization electromagnetic wave working at 3–30 MHz [1,2,3,4]. HF mixed-mode surface wave radar (MMSWR) is a new kind of monostatic high-frequency surface wave radar (HFSWR). The new propagation mode utilizes the echoes received from both surface-wave path and sky-wave path to obtain more information than a conventional monostatic HFSWR system. The diffuse scattering characteristic of targets makes it possible that a portion of echoes radiation will be reflected to the ionosphere. Under certain propagation conditions, including the range of the target, the ionosphere height and the reflection angle, this portion of radiation can be received by the antennas after a second reflection by ionosphere. This constitutes a multipath propagation model. Zhao et al. [5] presented a multipath propagation model for echo signals of islands to calculate the height of ionosphere. The echo signals of islands have two possible paths, the traditional ocean path where both the transmitted and received signal is via the surface wave, and the ocean-ionosphere path where the transmitted signal is via the surface wave and the reflected signal is received via the skywave path. Utilizing the same propagation model, a target track matching method is presented based on the multipath echoes by Zhang et al. [6]. A modified multimode target tracker is proposed to deal with the target tracking problem in mixed propagation mode [7]. The advantages of the mixed propagation mode compared with the conventional HFSWR, are that more target information can be obtained due to additional propagation paths and the detection range can be extended for HFSWR owing to the ionosphere propagation path. Therefore, these features have drawn increasing attention to the new HF MMSWR.

However, this new propagation mode introduces additional complexities. The combination of the surface path and the ionosphere path makes the clutter more difficult to handle than that of conventional HF radar [8]. The ionospheric clutter and the broaden sea clutter contaminated by ionosphere constitute the heterogeneous environment background for clutter suppression processing which presents the biggest problem. The nonhomogeneous first-order sea clutter masks low velocity ship targets with Doppler velocities near the Bragg frequency. Ionospheric clutter covers a wide range and Doppler area, and the high clutter energy requires that this clutter must be suppressed to enable target detection. To make things worse, the first-order sea clutter is contaminated by ionosphere which leads to broadening of the sea clutter. Therefore, the low velocity targets are more likely submerged by first-order sea clutter in this situation.

Space-time adaptive processing (STAP), proposed by Brennan and Reed [9,10], has become one of the major research directions to suppress nonhomogeneous clutter. The application of STAP to HFSWR requires an accurate estimation of the training data covariance matrix [11]. The independent, identically-distributed (IID) training samples with the clutter in the cell under test (CUT) are used to estimate the covariance matrix. Under this circumstance, it is assumed that the selected training samples are representative of the clutter in the CUT [12,13]. However, in HF MMSWR, the ionosphere transmission channel has high time-variation so that the clutter statistics change significantly. The first-order sea clutter is contaminated by ionosphere clutter, so the IID training samples with CUT are limited and some highly contaminated samples need to be eliminated from the training data. How to select these samples is a valuable research issue for the clutter suppression processing in HF MMSWR.

Many training sample selection algorithms have been proposed to improve the STAP performance in heterogeneous environment. The generalized inner product (GIP) algorithm [14] utilizes GIP to eliminate the samples through different clutter statistical characteristics from the CUT. The power-selected training (PST) algorithm [15] chooses the samples with the strong clutter power to deepen the clutter notch. The similarity detector (SD) algorithm [16,17,18,19] selects the samples with waveforms that are similar to the CUT. Recently, the information geometry-based SD algorithm has drawn more attentions on covariance estimation and target detection processing [20,21,22,23,24]. A class of covariance matrix estimators, which are associated with suitable distances in the considered space and defined as the geometric barycenter, are proposed to exclude the outliers and clutter for target detection in [25,26]. It has been shown that the information geometry-based methods yield significant performance gains as compared with conventional covariance estimators and detectors. In this paper, we combine the geometric barycenter-based covariance estimation algorithm with the reduced-dimension STAP method to overcome the heterogeneous clutter in HF MMSWR.

This paper is organized as follows. In Section 2, the signal model and the range correlation of the first-order sea clutter in a practical HF MMSWR system is formulated. A geometric barycenter-based reduced-dimension STAP algorithm is proposed in Section 3. The performance of training data selectors is analyzed based on the simulation of a practical system in Section 4 and the effectiveness of the proposed method is verified by suppress of the sea clutter and ionospheric clutter using the experimental data in Section 5. Finally, conclusions are presented in Section 6.

2. Data Model and Clutter Statistic Analysis

2.1. Signal Model

Figure 1 shows the geometric model of the HF MMSWR system. As discussed above, the surface wave radiation, which is a solid blue line, may have two echo paths, the surface wave echo (dotted red line) and the sky wave echo (dotted green line). However, in the practical system, the transmitting radiation cannot be strictly controlled along the horizontal direction. A portion of the radiation will be transmitted at a higher angle towards the ionosphere, which is shown as the solid orange line. Thus, there will be four possible propagation paths consisting the mixed propagation mode.

Figure 2 shows the receiving array configuration. Consider a $N$-channel uniform linear array (ULA) and the sensor spacing is $d$, the carrier wavelength is $\lambda$. The number of signal pulses collected in one coherent processing interval (CPI) for each channel is $M$. The echo of the $i$-th range bin can be expressed as

$$x_i=\alpha \left(i\right)s\left(f,\theta \right)+c\left(i\right)+n\left(i\right)$$

(1)

where $\alpha \left(i\right)$, $c\left(i\right)$ and $n\left(i\right)$ denote complex amplitude, clutter and noise, respectively. $s\left(f,\theta \right)=s_{tem}\left(f\right)\otimes s_{spa}\left(\theta \right)$ denotes the target vector, $\otimes$ is the Kronecker product,

$$s_{tem}\left(f\right)={\left[\begin{array}{cccc}1& \exp \left(j2\pi f\right)& \cdots & \exp \left(j2\pi \left(M-1\right)f\right)\end{array}\right]}^T$$

(2)

$$s_{spa}\left(\theta \right)={\left[\begin{array}{cccc}1& \exp \left(j2\pi d\sin \theta /\lambda \right)& \cdots & \exp \left(j2\pi \left(N-1\right)d\sin \theta /\lambda \right)\end{array}\right]}^T$$

(3)

which represent the temporal steering vector, which is $M\times 1$ and the spatial steering vector, which is $N\times 1$. ${(\cdot )}^T$ is the transpose process.

2.2. Range Correlation Analysis

The clutter statistics are the foundation of the clutter suppression algorithm design. In the HF MMSWR system, the non-stationary nature of the echo data in range cell is the major problem of clutter suppression processing. The sea clutter statistics change significantly across even neighboring range units. Therefore, we do the correlation analysis on measured data to show the necessity of the training data selection.

In the range domain, the correlation coefficient of the data in different range bins can be calculated by,

$${\eta }_{i,j}=\frac{\left(1/N_{f_d}\right){\displaystyle {\sum }_{N_{f_d}}{Z}_b\left(i,f_d\right)Z_b^H\left(j,f_d\right)}}{\sqrt{{\left(1/N_{f_d}\right)}^2{\displaystyle {\sum }_{N_{f_d}}{\left|Z_b\left(i,f_d\right)\right|}^2}{\displaystyle {\sum }_{N_{f_d}}{\left|Z_b^H\left(j,f_d\right)\right|}^2}}}$$

(4)

where $N_{f_d}$ is the number of the sample Doppler bin, $i$ is the reference range bin and $j=1,2,\dots ,R$ is the whole range bins which is under analysis, $Z_b$ is the sample data in the beam bin $b$ with Doppler shift $f_d$, and ${(\cdot )}^H$ represents the complex conjugate operation. Figure 3 shows the typical range correlation result of the sea clutter echo in the HF MMSWR system. It shows the negative Bragg peak with Doppler frequency of $f=-0.2602 \mathrm{Hz}$ and beam point at $b=0^{\circ }$. The reference range bin is $i=76$. The strong correlation threshold is set to be 0.8, as the red dotted line shows. This indicates that sea clutter statistics changes rapidly in different range bins. Therefore, the training sample selection strategy is of vital importance to select the effective training data and discard the interference such as ionosphere clutter.

3. Geometric Barycenter-Based Reduced-Dimension STAP Algorithm

3.1. Joint Domain Localized Processing

Full dimension STAP algorithm can provide good clutter suppression performance with all the channels and pulses used to calculate the optimal weight. In order to approach the optimal performance of 3 dB loss, the total of $2NM$ IID training samples are required. So the computational cost of directly inverting a $\left(NM\times NM\right)$ dimensional matrix is of order $O{\left(NM\right)}^3$, which is pretty high [27]. In a practical HF MMSWR system, suppose $N=8$ and $M=5120$, so that the total number of the IID training data will be 81,920 in the range domain which is unrealistic in an operational system. Therefore, the reduced-dimension STAP algorithm is needed for the HF MMSWR system.

Joint domain localized processing is a powerful reduced-dimension STAP processing [28]. It transforms the whole training data to a localized processing region (LPR) by a transformation matrix.

For a certain range bin $k$, the $NM\times 1$ dimensional vector of the space-time snapshots is given by,

$$X_k={\left[\begin{array}{cccc}{\mathrm{x}}_1& {\mathrm{x}}_2& \cdots & {\mathrm{x}}_M\end{array}\right]}^T$$

(5)

$${\mathrm{x}}_i={\left[\begin{array}{cccc}{x}_{1,i}& x_{2,i}& \cdots & x_{N,i}\end{array}\right]}^T,\hspace{1em}i=1,2,\dots ,M$$

(6)

The space-time steering vector $s\left(f,\theta \right)$ is defined as,

$$s\left(f_c,{\theta }_c\right)=s_t\left(f_c\right)\otimes s_s\left({\theta }_c\right)$$

(7)

where $s_t$ and $s_s$ are the time steering vector and space steering vector defined above, respectively.

The transformation matrix $\mathbf{T}$ is used to transform the range samples to an angle-Doppler region in order to reduce the degree of freedom (DOF). It can be written as,

$$\begin{array}{cc}\mathbf{T}& =\left[\begin{array}{ccccc}{s}_t\left(f_{c-\left(p-1\right)/2}\right)& \cdots & s_t\left(f_c\right)& \cdots & s_t\left(f_{c+\left(p-1\right)/2}\right)\end{array}\right]\\ & \otimes \left[\begin{array}{ccccc}{s}_s\left({\theta }_{c-\left(q-1\right)/2}\right)& \cdots & s_s\left({\theta }_c\right)& \cdots & s_s\left({\theta }_{c+\left(q-1\right)/2}\right)\end{array}\right]\end{array}$$

(8)

Here $\mathbf{T}$ is a $NM\times pq$ dimension transform matrix. The localized processing range samples and the space-time steering vector after the transformation process are given by,

$${\widehat{X}}_k={\mathbf{T}}^H\cdot X_k,\hspace{1em}\widehat{s}={\mathbf{T}}^H\cdot s$$

(9)

The covariance matrix is calculated utilizing $\mathsf{\Omega }$ training samples in range domain which is chosen to represent the clutter information in the CUT.

$${\widehat{\mathit{R}}}_k=\frac{1}{\mathsf{\Omega }}{\displaystyle \sum _1^{\mathsf{\Omega }}{\widehat{X}}_{\omega }{\widehat{X}}_{\omega }^H}$$

(10)

where ${\widehat{X}}_{\omega }$ is the chosen training sample from the whole range domain, $\omega \in \left\{1,2,\dots ,k-2,k+2,\dots ,K\right\}$, where $K$ is the total range cell of interest. The range bin $k,k-1,k+1$, which is the cell under test and two guard cells, are not taken as the training sample to prevent the target self-elimination.

Then, the adaptive weights can be expressed as,

$$W_{opt}={\widehat{\mathit{R}}}^{-1}\cdot \widehat{s}$$

(11)

The joint domain localized (JDL) algorithm solves the first problem of the training samples starve scenario for that $\mathsf{\Omega }=2pq$ which is much less than $2NM$. But how to select the efficient training samples in the training dataset needs the training data selection method.

3.2. Geometric Barycenter-Based Training Data Selector

The geometric barycenter-based covariance matrix estimation algorithms have drawn lots of attention [25,26]. The covariance estimators are associated with suitable distances, defined as the geometric barycenter of covariance matrix estimates, in the considered space. Computed from a secondary dataset, the barycenter distances are used to determine each training sample, sufficient or not, and exclude the outliers as well as clutter for target detection. The design of these estimators did not require knowledge of the statistical characterization of the whole training data. This feature makes the information geometry-based training data selector very suited to select the most homogeneous clutter samples in the background of the highly non-stationary environment. Here, we consider a set of geometric barycenter covariance matrix estimators associated with suitable distances. The distances we choose to define the similarity of the training samples’ covariance matrix are focused on the Euclidean, root-Euclidean, power-Euclidean, and log-Euclidean distances. These distances define the specific functions (identity, root, power, and log) that the matrices are transformed. The benefits from this transformation processing are that these transformations can be seen as compressors of eigenvalues which can mitigate the effect of outliers and clutter.

Firstly, we give the expression of the geometric barycenter-based covariance matrix estimators. Let $\mathit{R}=\frac{1}{\mathsf{\Omega }}{\displaystyle \sum _1^{\mathsf{\Omega }}{x}_{\omega }{x}_{\omega }^H}$ denote the positive-definite covariance matrix. $x_{\omega },\omega =1,2,\dots ,\mathsf{\Omega }$ are the $N$-dimensional random vectors with an arbitrary joint statistical distribution and let them share the same covariance matrix $\mathit{R}$. Then we assume that ${\mathit{S}}_{\omega },\omega =1,2,\dots ,\mathsf{\Omega }$ are the covariance matrix estimates and $d\left(\mathit{A},\mathit{B}\right)\in \left[0,+\infty \right)$ denotes the geometric distance between the two matrices. The covariance matrix estimator based on geometric barycenter can be defined as

$$\widehat{\mathit{R}}=\arg \underset{\mathit{R}\succ 0}{\min }\left\{{\displaystyle \sum _{\omega =1}^{\mathsf{\Omega }}{w}_{\omega }{d}^2\left({\mathit{S}}_{\omega },\mathit{R}\right)}\right\}$$

(12)

Here, without a priori knowledge, we set the coefficients to be equal, $w_{\omega }=1/\mathsf{\Omega },\omega =1,2,\dots ,\mathsf{\Omega }$.

The four barycenter distances and the corresponding estimators can be defined as follows:

• Euclidean distance and estimator

  $$d_E\left(\mathit{A},\mathit{B}\right)=\sqrt{tr\left\{\left(\mathit{A}-\mathit{B}\right){\left(\mathit{A}-\mathit{B}\right)}^H\right\}}$$

  (13)

  $${\widehat{\mathit{R}}}_E=\arg \underset{\mathit{R}\succ 0}{\min }\left\{{\displaystyle \sum _{\omega =1}^{\mathsf{\Omega }}{w}_{\omega }{d}_E{}^2\left({\mathit{S}}_{\omega },\mathit{R}\right)}\right\}$$

  (14)
• Root-Euclidean distance and estimator

  $$d_{rE}\left(\mathit{A},\mathit{B}\right)=\sqrt{tr\left\{\left(\sqrt{\mathit{A}}-\sqrt{\mathit{B}}\right){\left(\sqrt{\mathit{A}}-\sqrt{\mathit{B}}\right)}^H\right\}}$$

  (15)

  $${\widehat{\mathit{R}}}_{rE}=\arg \underset{\mathit{R}\succ 0}{\min }\left\{{\displaystyle \sum _{\omega =1}^{\mathsf{\Omega }}{w}_{\omega }{d}_{rE}{}^2\left({\mathit{S}}_{\omega },\mathit{R}\right)}\right\}$$

  (16)
• Power-Euclidean distance and estimator

  $$d_{pE}\left(\mathit{A},\mathit{B}\right)=\sqrt{tr\left\{\left({\mathit{A}}^{\alpha }-{\mathit{B}}^{\alpha }\right){\left({\mathit{A}}^{\alpha }-{\mathit{B}}^{\alpha }\right)}^H\right\}}$$

  (17)

  $${\widehat{\mathit{R}}}_{pE}=\arg \underset{\mathit{R}\succ 0}{\min }\left\{{\displaystyle \sum _{\omega =1}^{\mathsf{\Omega }}{w}_{\omega }{d}_{pE}{}^2\left({\mathit{S}}_{\omega },\mathit{R}\right)}\right\}$$

  (18)
• Log-Euclidean distance and estimator

  $$d_{pE}\left(\mathit{A},\mathit{B}\right)=\sqrt{tr\left\{\left({\mathit{A}}^{\alpha }-{\mathit{B}}^{\alpha }\right){\left({\mathit{A}}^{\alpha }-{\mathit{B}}^{\alpha }\right)}^H\right\}}$$

  (19)

  where $\log \mathit{A}={\mathit{U}}_A\mathbf{diag}\left({\mathit{\lambda }}_A^{lE}\right){\mathit{U}}_A^H$, with ${\mathit{\lambda }}_A^{lE}=\left[\log \left({\mathit{\lambda }}_1^A\right),\log \left({\mathit{\lambda }}_2^A\right),\dots ,\log \left({\mathit{\lambda }}_N^A\right)\right]$.

  $${\widehat{\mathit{R}}}_{lE}=\arg \underset{\mathit{R}\succ 0}{\min }\left\{{\displaystyle \sum _{\omega =1}^{\mathsf{\Omega }}{w}_{\omega }{d}_{lE}{}^2\left({\mathit{S}}_{\omega },\mathit{R}\right)}\right\}$$

  (20)

Then we need to find a way to compute these estimators. The following theorem, given in [25], allows us to obtain the closed form expression of these estimators.

Theorem: Given the set of matrices $A_i\in {ℂ}^{N\times N}$, $i=1,2,\dots ,K$, and the set of weights $w_i$, $i=1,2,\dots ,K$, with $w_i>0$ and ${\displaystyle {\sum }_{i=1}^K{w}_i=1}$, the solution to the optimization problem

$$\widehat{A}=\arg \underset{A}{\min }\left\{{\displaystyle \sum _{i=1}^K{w}_i{\Vert A_i-A\Vert }^2}\right\}$$

(21)

is unique, and can be written as

$$\widehat{A}={\displaystyle \sum _{i=1}^K{w}_i{A}_i}$$

(22)

• The proof of the theorem can be seen in [25]. With the theorem, we can compute the closed form expression of the covariance matrix estimators utilizing the geometric distance mentioned above. Euclidean estimator

Let $A_i={\mathit{S}}_{\omega },i=\omega$, ${\mathit{S}}_{\omega }$ is the $\omega \mathrm{th}$ estimate, $A=\mathit{R}$, the Euclidean estimators can be computed as,

$${\widehat{\mathit{R}}}_E={\displaystyle \sum _{\omega =1}^{\mathsf{\Omega }}{w}_{\omega }{\mathit{S}}_{\omega }}$$

(23)

• Root-Euclidean estimator

Let $A_i={\mathit{S}}_{\omega }^{1/2}$, $A={\mathbf{\Delta }}_{rE}={\mathit{R}}^{1/2}$, the root-Euclidean estimator is

$${\widehat{\mathit{R}}}_{rE}={\widehat{\mathbf{\Delta }}}_{rE}{\widehat{\mathbf{\Delta }}}_{rE}^H,\mathrm{where}{\widehat{\mathbf{\Delta }}}_{rE}={\displaystyle \sum _{\omega =1}^{\mathsf{\Omega }}{w}_{\omega }{\mathit{S}}_{\omega }^{1/2}}$$

(24)

• Power-Euclidean estimator

Let $A_i={\mathit{S}}_{\omega }^{\alpha }$, $A={\mathbf{\Delta }}_{pE}={\mathit{R}}^{\alpha }$, the power-Euclidean estimator is

$${\widehat{\mathit{R}}}_{pE}={\left({\widehat{\mathbf{\Delta }}}_{pE}\right)}^{1/\alpha },\mathrm{where}{\widehat{\mathbf{\Delta }}}_{pE}={\displaystyle \sum _{\omega =1}^{\mathsf{\Omega }}{w}_{\omega }}{\mathit{S}}_{\omega }^{\alpha }$$

(25)

• Log-Euclidean estimator

Let $A_i=\log {\mathit{S}}_{\omega }$, $A=\log \mathit{R}$, the log-Euclidean estimator is

$${\widehat{\mathit{R}}}_{lE}=\exp \left\{{\displaystyle \sum _{\omega =1}^{\mathsf{\Omega }}{w}_{\omega }\log {\mathit{S}}_{\omega }}\right\}$$

(26)

where $\exp \mathit{A}={\mathit{U}}_{A}diag\left({\mathit{\lambda }}_A^{lE}\right){\mathit{U}}_A^H$, with ${\mathit{\lambda }}_A^{lE}=\left[\exp \left({\mathit{\lambda }}_1^A\right),\exp \left({\mathit{\lambda }}_2^A\right),\dots ,\exp \left({\mathit{\lambda }}_N^A\right)\right]$.

Using the geometric distance and corresponding estimators above, we can design the training data selector. As discussed above, the characteristic of the first-order sea clutter in range domain changes rapidly in the HF MMSWR system. The independent identically distributed request for the training data cannot be satisfied for space-time adaptive processing in practical scenarios. The multipath propagation, the ionospheric disturbance, and the interference make it impossible for all the training data to share the homogeneity properties. Therefore, the training data selector is designed to select the most “similar” training data with the cell under test. The chosen training data can represent the clutter information of the cell under test more accurately and provide better performance for STAP.

Unlike some target detectors in [22,23,26], which detect the target with the highest geometric distances, we choose the training data with the lowest geometric distances because the lower geometric distance shows more homogeneity with the cell under test. The training data selection strategy is processed as follows,

• Calculate the covariance matrices ${\mathit{\Lambda }}_i={\widehat{X}}_i{\widehat{X}}_i^H,i=1,2,\dots ,K$ for a single range bin $i$, defined in Section 3.1;
• Suppose the range bin for the cell under test is $k$, calculate the geometric distances $d\left({\mathit{\Lambda }}_k,{\mathit{\Lambda }}_i\right)$ and covariance estimator $\widehat{\mathit{R}}$ for all the training data in range domain;
• Calculate the generalized inner product ${\beta }_i={\widehat{X}}_i^H{\widehat{\mathit{R}}}^{-1}{\widehat{X}}_i,i=1,2,\dots ,K$ for all the training data;
• Set ${\beta }_k={\beta }_{k-1}={\beta }_{k+1}=\max \left\{{\beta }_i\right\}$ as guard cells to prevent the target self-elimination and sort ${\beta }_i$s in ascending order;
• Select the $\mathsf{\Omega }=2pq$ indices as the training samples which correspond to $\mathsf{\Omega }$ lowest values of ${\beta }_i$.

Using the $\mathsf{\Omega }$ training samples chosen, clutter suppression can be undertaken utilizing the joint domain localized processing discussed above. Processing all the range bins and Doppler bins in turn, we obtain the clutter suppression output that is then forwarded to the detector and on to the tracker.

4. Simulation Results

In this section, we present the performance analysis of the proposed training data selectors. We assume the covariance matrix is constructed by the sum of the clutter covariance matrix and noise matrix which is an identity matrix [26],

$$\mathit{R}={\sigma }_c^2{\rho }^{\left|m-n\right|}{e}^{j2\pi f_{d_c}\left(m-n\right)}+p_0{\mathit{I}}_{noise},\hspace{1em}m,n=1,2,\dots ,N$$

(27)

where ${\sigma }_c^2$ is the clutter-to-noise ratio, $\rho$ is the one-lag correlation coefficient, $f_{d_c}$ is the clutter normalized Doppler frequency, $p_0$ is the diagonal loading coefficient. To simulate the real situation of the first-order clutter in the HF MMSWR system, the total secondary data in range domain is set to be $K=100$. The LPR we use is $5\times 3$, so that the required number of training samples is $\mathsf{\Omega }=2\times p\times q=30$. The number of the guard cell is two. To simulate the impact of the ionospheric disturbance on sea clutter, we inject two sets of disturbances whose normalized Doppler frequency is slightly different from that of the sea clutter. The temporal steering signature is,

$$\mathit{t}=\alpha {\left[1,e^{j2\pi f_{d_o}},\dots ,e^{j2\pi \left(N-1\right)f_{d_o}}\right]}^T$$

(28)

where $\alpha$ is the amplitude of the disturbance, $f_{d_o}$ is the normalized Doppler frequency of the disturbance. The performance of the different training data selectors is analyzed by 5000 Monte Carlo simulations, evaluating the rate that a correct selection occurs, which means selecting 30 training samples with no disturbance.

In a practical HFSWR system, the sea clutter statistical property is usually affected by two factors. The first factor is the total number of the training samples corrupted by ionospheric disturbance. The second factor is the similarity of the ionospheric disturbance and the sea clutter statistics in the CUT. In the following subsections we undertake the simulation performance analysis based on these two factors.

4.1. Selection Performance with Number of Disturbances

Firstly, we do the performance analysis against average disturbance power with different numbers of disturbances. The simulation conditions are that $N=8$, $K=100$, $\mathsf{\Omega }=30$, ${\sigma }_c^2=15$ dB, $\rho =0.95$, $f_{d_c}=0.20$, $p_0=1$, the number of Monte Carlo simulation is 5000, the normalized Doppler frequency of the first set of disturbances belongs to $\left\{f_{d_{o,1}}\right\}\in \left\{0.15\pm 0.01\right\}$ and the second set is set to be $\left\{f_{d_{o,2}}\right\}\in \left\{0.25\pm 0.01\right\}$. The power of each disturbance is assumed equal. Figure 4 shows the selection performance when the total number of disturbances $N_{disturbance}$ are 6, 8, 10, and 12, respectively. Figure 4 shows that the Log-Euclidean distance-based training data selector has the best performance and selects the most homogeneous training data among the different disturbances. This result agrees with the conclusions by Aubry et al. [25] and Cui et al. [26]. This shows that the Log-Euclidean estimator outperforms other geometric barycenter estimators in different conditions, for both target detection processing and clutter suppression processing. As the number of the disturbance increases, which is from 6 to 12 in (a) to (d), respectively, the correct selection rate decreases as it was expected. This implies that the first-order sea clutter in the practical situation suffers more ionospheric disturbances which makes the clutter statistical property more heterogeneous. Therefore, the correct selection becomes more difficult. But even in this scenario, the Log-Euclidean selector shows greater robustness than the others, especially the Euclidean selector.

4.2. Selection Performance with Disturbance Doppler Frequency

In this section, we analyze the selection performance against different kinds of disturbances which means the normalized Doppler frequency of disturbances are different. The same simulation setup is used as described in Section 4.1, with the exception that the normalized Doppler frequency of the two disturbances changes. The total number of the disturbance $N_{disturbance}$ was set to eight. Figure 5 shows the performance analysis of four situations with different normalized Doppler frequency of disturbance. The difference value between the disturbance and the clutter is decreasing from (a) to (d) and the correct selection rate tends to degrade for each selector. This means that the disturbance is more difficult to exclude when its characteristic is more homogeneous with the clutter under test. Among all the estimators, the Log-Euclidean estimator still outperforms others and suffers less severe performance degradation.

As the simulation results show in Section 4.1 and Section 4.2, the Log-Euclidean estimator has the best performance with respect to selecting the most efficient training data. It is chosen as the training data selector in the proposed method to do the clutter suppression. The experimental results, given in the next section, are based on the Log-Euclidean estimator.

5. Experimental Results

In this section, we apply the proposed training data selection method to the sea clutter suppression processing in the practical system. The Log-Euclidean selector is chosen to select the training samples as it outperforms others. As discussed in Section 3, we propose a novel geometric barycenter-based reduced-dimension space-time adaptive processing combining the Log-Euclidean selector with the JDL processing. The measured data are collected by the experimental HF OTHR system developed by the Harbin Institute of Technology in 2015. The receiving array is a 16 channel ULA with a 10-m sensor interval. The radar signal is phase-coded signal and the carrier frequency is 10.91 MHz, with a bandwidth of 40 kHz and pulse repetition frequency (PRF) of 66.67 Hz.

5.1. Measured Data with Simulated Target

We injected a simulated target in the No. batch 24 measured dataset. The Doppler frequency is 0.2995 Hz, the target direction is 9° and the range cell is at 72. It is close to the positive Bragg peak, which cannot be detected due to the strong first-order sea clutter. The localized processing region (LPR) we choose is $3\times 3$ in Doppler domain and azimuth domain. Therefore, the number of training samples we select is 18.

Figure 6a,b show the range-Doppler map of the digital beam forming (DBF) method and the Log-Euclidean JDL (LE-JDL) method with the injected target respectively. It shows that the first-order sea clutter has been suppressed to a large extend as compared with the DBF method. But the spread ionospheric clutter in about 100 range bins remain pretty strong which will still make it difficult to detect the targets around this region. The ionospheric clutter suppression is discussed in the following subsection.

Figure 7 shows the Doppler profile results of the No. 72 range bin which displays the clutter suppression performance clearly. The experimental data are processed by the DBF method, the conventional JDL method, and the proposed LE-JDL method, respectively. The first two methods are performed as comparisons with the LE-JDL method. From the figure, it is clearly that the performance of LE-JDL outperforms the conventional JDL. The first-order sea clutter has been suppressed by 20.5 dB for negative Bragg peak and 30.3 dB for positive Bragg peak, which is almost entirely suppressed. The signal-clutter-ratio (SCR) improves from −5.8 dB to 17.1 dB, and the target can be easily detected after the clutter suppression. In addition, the conventional JDL method is not very valid due to the nonhomogeneous environment of HF MMSWR. The invalid training samples degrade the suppression performance and the SCR only increases to 5.1 dB, which is difficult to be detected.

5.2. Measured Data with Non-Cooperative Target

We select a non-cooperative target from the experimental dataset in order to investigate the effectiveness of the proposed method in the practical situation. The Doppler frequency of the target is −0.5078 Hz, the target direction is 0° and the range cell is at 69. The LPR we choose is the same as Section 5.1.

Figure 8 shows the clutter suppression result with the target in the range-Doppler map. Figure 8a is the range-Doppler map of the DBF process as the comparison and Figure 8b is the result of the proposed LE-JDL method. From the figures, we can see clearly that the proposed method is very powerful to suppress the first-order sea clutter in the non-stationary background environment.

To show the validity of the proposed method visually, we also give the Doppler profile result of three methods at the target range bin in Figure 9. The LE-JDL method suppresses the negative Bragg peak of the first-order sea clutter by 23.1 dB and 22.2 dB for the positive Bragg peak. The average clutter power reduction is 22.65 dB, and the target energy remains strong at the same time. The SCR between target and the negative Bragg peak improves from −0.3 dB to 18.3 dB. It provides convenience for the following target detection and tracking process for the slow velocity vessels whose Doppler frequency are close to the Bragg peaks. The conventional JDL method still suffers from invalid training samples in non-stationary environment.

5.3. Measured Data with Ionospheric Clutter

The proposed RD-STAP method is valid for ionospheric clutter as well. The strip-type ionospheric clutter occurred during the experiment time, usually formed by Es layer. Unlike the sea clutter, the strip-type ionospheric clutter only occupies a few cells in range domain, but it covers a large number of Doppler cells. Therefore, in range domain, it suffers less from other kinds of disturbance and the characteristics differs from the sea clutter and background noise significantly. To show the validity of the proposed method, we also give the range-Doppler map of the DBF method and our method, as well as the Doppler profile result. The range cell chosen is at range cell 23 where the strip-type ionospheric clutter occurs.

Figure 10 and Figure 11 give the ionospheric clutter suppression results. It is worthwhile to notice that due to the lack of range samples for the strip-type ionospheric clutter, the number of training data we select is 12 in order to obtain a good clutter suppression performance. However, it does not satisfy the requirement of 3 dB signal loss which is $\mathsf{\Omega }=2pq=18$. Therefore, this means that we have to sacrifice the target energy and the sea clutter suppression performance to gain a high ionospheric clutter suppression performance. Further research of this strip-type ionospheric clutter, which covers only a small amount of range bins, could be the goal of future research.

6. Conclusions

In this paper, an effective geometric barycenter-based reduced-dimension STAP method, which we call LE-JDL, is proposed for the first-order sea clutter suppression in the background of the HF mixed-mode surface wave radar system. The range correlation is first analyzed for the measured data to guide the clutter suppression algorithm design. In order to apply the conventional JDL algorithm to the heterogeneous environment in the practical HF MMSWR system, a training data selector, which is based on geometric barycenter, is applied. The performance of four kinds of selectors are analyzed, and the Log-Euclidean selector is chosen. The validity of the proposed method is verified by using the experimental data. The results show that the LE-JDL method has the ability to suppress the non-stationary sea clutter in the HF MMSWR system while the conventional JDL algorithm is invalid. It can improve the SCR of the target and increase the target detection probability for slow velocity vessels. As well, the proposed method is also capable of ionospheric clutter suppression in certain conditions.