A Sensitivity Study of POD Using Dual-Frequency GPS for CubeSats Data Limitation and Resources
Abstract
:1. Introduction
2. Processing Strategy
- Compute kinematic orbits using single point positioning (SPP) employing the IF combination of the code observations. These kinematic orbits, denoted as vector , are discrete and have an accuracy of meters.
- Computation of the code-based reduced-dynamic orbits. The reduced-dynamic orbits are computed with accelerations based on a series of gravitational and nongravitational terms, such as the Earth gravitational terms, the Earth tidal terms, the gravitational attraction from the sun, moon, and other planets, as well as the general relativistic term. Note that mis-modeled effects like the solar radiation pressure and the air drag will be largely absorbed by the estimated dynamic parameters and the stochastic velocity changes or accelerations set up later in the processing [35]. Details of the processing and the dynamic models are given in Table 1. Making use of the kinematic code orbits from the first step, the six Keplerian elements at the initial condition (the semi-major axis of the orbit, the orbital eccentricity, the inclination of the orbital plane, the right ascension of the ascending node, the argument of perigee, and the argument of latitude at the initial condition), and a remaining part of the dynamic models are estimated with a batch least-squares adjustment, which includes at this step nine flight-oriented dynamic parameters. These estimable dynamic parameters contain three constant terms (, , and ) and six periodic terms (, , , , , and ) in the radial (R), along-track (S) and cross-track (W) directions. The total acceleration can then be distributed into the term , which is assumed known by applying the models given in Table 1, and an additional dynamic term that is to be adjusted:Withwhere , , and represent the unit vectors in the radial, along-track, and cross-track directions, respectively. denotes the satellite argument of latitude. The code-based kinematic orbits obtained from the first step are used as observations to adjust the 15 parameters mentioned above in a least-squares sense. The linearized observation equation at the epoch can be formulated as:where is the a priori orbit vector obtained based on numerical integration on hand the , and the and the Keplerian elements estimated from the last iteration. The vectors and contain the increments of the six Keplerian elements and the nine dynamic parameters, respectively, and the design matrices and contain the partial derivatives of the position vectors with respect to and . The partial derivatives are computed with numerical integration of the variational equations [36,37]. is the expectation operator. The reduced-dynamic orbit can be interpolated for time epochs with higher sampling rates and produced for periods with data gaps. In this study, all orbits are resampled into time epochs with 10 s sampling interval for assessment, regardless of which duty-cycles and observation sampling rates are applied in the processing.
- 3.
- Phase preprocessing and orbit improvements. This step preprocesses the raw phase observations to detect cycle slips and mark bad observations. The preprocessing goes through several iterations to improve the LEO orbit quality. The orbit improvement is realized through estimation of stochastic velocity changes [38] in addition to the 15 parameters mentioned in the second step, and is performed in a least-squares adjustment making use of the IF combination of the phase observations. One set of the stochastic velocity changes is considered in each predefined time interval, e.g., every 15 min. The linearized phase observation equation at the epoch can be expressed as:Withwhere ∆φIF represents the observed-minus-computed (O-C) term of the IF phase observations. c and Δtr denote the speed of light and the receiver clock error, respectively. λj, fj, and Nj represent the wavelength, the frequency, and the ambiguity on frequency j (j = 1, 2), respectively. Note that NIF is not an integer. The receiver clock error is estimated epoch-wise independently, and the ambiguity is assumed constant before the detection of a cycle slip. Note that new ambiguities are setup for estimation at the beginning of each round of duty cycling. xv stands for the vector containing all stochastic velocity changes in the RSW directions from the first to the current epoch and note that xv is constrained to zero with a predefined a priori standard deviation. The design matrices Alk, Ald, and Alv contain the partial derivatives of the O-C terms with respect to the xk, xd, and xv, respectively. To be estimated are the vector [xk,xd,xv]T, the receiver clock offset Δtr, and the term NIF. Note that very little code observations are used to avoid the problem of matrix singularity between the receiver clock offset and the ambiguity terms. Note that the ambiguities on L1 and L2 are not attempted to be fixed in this study.
- 4.
- Generation of final orbits. With the preprocessed phase observations, the six Keplerian elements, the three constant dynamic parameters (, , and ) are estimated together with stochastic accelerations in the RSW directions. The accelerations are set up in shorter time intervals compared to those in Step 3. The linearized phase observation equation is thus formulated as:where and denote the increment vector of the three constant dynamic parameters and all the stochastic accelerations from the first to the current epoch, respectively. is constrained to zero with a predefined a priori standard deviation (selected as 5 m/ in all the three directions based on the default setting for GRACE satellites in the Bernese software, as real data from the GRACE Follow-on mission is used for test purposes in this study, which will be explained later. This value may vary for satellites of other missions). and correspond to the partial derivatives of the phase O-C terms with respect to the and , respectively. Note that very little code observations are used to avoid singularity mentioned above.
3. Orbit Determination under Different Scenarios
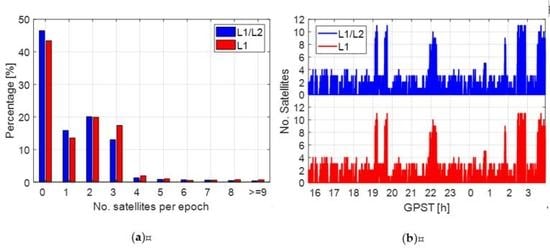
3.1. Duty Cycling and Satellite Numbers
3.2. Sampling Rate of the Observations
3.3. Latency Applying Different GPS Products
3.4. Antenna Attitude
3.5. Length of Arc
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yunck, T.P.; Wu, S.C.; Wu, J.T.; Thornton, C.L. Precise tracking of remote-sensing satellites with the global positioning system. IEEE Trans. Geosci. Remote Sens. 1990, 28, 108–116. [Google Scholar] [CrossRef]
- Montenbruck, O. An epoch state filter for use with analytical orbit models of low earth satellites. Aerosp. Sci. Technol. 2000, 4, 277–287. [Google Scholar] [CrossRef]
- Svehla, D.; Rothacher, M. Kinematic and reduced-dynamic precise orbit determination of low earth orbiters. Adv. Geosci. EGU 2003, 2003, 1, 47–56. [Google Scholar]
- Jäggi, A.; Hugentobler, U.; Bock, H.; Beutler, G. Precise orbit determination for GRACE using undifferenced or doubly differenced GPS data. Adv. Space Res. 2007, 39, 1612–1619. [Google Scholar] [CrossRef]
- Haines, B.; Bar-Sever, Y.; Bertiger, W.; Desai, S.; Willis, P. One-Centimeter Orbit Determination for Jason-1: New GPS-Based Strategies. Mar. Geod. 2004, 27, 299–318. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Drinkwater, M.R.; Floberghagen, R.; Haagmans, R.; Muzi, D.; Popescu, A. GOCE: ESA’s first earth explorer core mission. In Earth Gravity Field from Space—From Sensors to Earth Sciences; Beutler, G., Drinkwater, M.R., Rummel, R., Von Steiger, R., Eds.; Part of the Space Sciences Series of ISSI Book Series (Volume 17); Springer: Dordrecht, The Netherlands, 2003; pp. 419–432. [Google Scholar]
- Wickert, J.; Reigber, C.; Beyerle, G.; König, R.; Marquardt, C.; Schmidt, T.; Grunwaldt, L.; Galas, R.; Meehan, T.K.; Melbourne, W.G.; et al. Atmosphere sounding by GPS radio occultation: First results from CHAMP. Geophys. Res. Lett. 2001, 28, 3263–3266. [Google Scholar] [CrossRef] [Green Version]
- Crétaux, J.F.; Bergé-Nguyen, M.; Calmant, S.; Jamangulova, N.; Satylkanov, R.; Lyard, F.; Perosanz, F.; Verron, J.; Montazem, A.S.; Le Guilcher, G.; et al. Absolute calibration or validation of the altimeters on the Sentinel-3A and the Jason-3 over Lake Issykkul (Kyrgyzstan). Remote Sens. 2018, 10, 1679. [Google Scholar] [CrossRef] [Green Version]
- Tu, J.; Gu, D.; Wu, Y.; Yi, D. Error modeling and analysis for InSAR spatial baseline determination of satellite formation flying. Math. Probl. Eng. 2012, 2012, 140301. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E.; Kroes, R. Rapid orbit determination of LEO satellites using IGS clock and ephemeris products. GPS Solut. 2005, 9, 226–235. [Google Scholar] [CrossRef]
- Gu, D.; Ju, B.; Liu, J.; Tu, J. Enhanced GPS-based GRACE baseline determination by using a new strategy for ambiguity resolution and relative phase center variation corrections. Acta Astronaut. 2017, 138, 176–184. [Google Scholar] [CrossRef]
- Kroes, R.; Montenbruck, O.; Bertiger, W.; Visser, P. Precise GRACE baseline determination using GPS. GPS Solut. 2005, 9, 21–31. [Google Scholar] [CrossRef]
- Ju, B.; Gu, D.; Herring, T.A.; Allende-Alba, G.; Montenbruck, O.; Wang, Z. Precise orbit and baseline determination for maneuvering low earth orbiters. GPS Solut. 2015, 21, 53–64. [Google Scholar] [CrossRef] [Green Version]
- Jäggi, A.; Arnold, D. Precise Orbit Determination. In Global Gravity Field Modeling from Satellite-to-Satellite Tracking Data; Naeimi, M., Flury, J., Eds.; Part of the Lecture Notes in Earth System Sciences Book Series; Springer International Publishing: Cham, Switzerland, 2017; pp. 35–80. [Google Scholar]
- NanoSats Database. World’s Largest Database of Nanosatellites, over 2500 Nanosat and CubeSats. Available online: https://www.nanosats.eu/ (accessed on 30 April 2020).
- Douglas, E.S.; Cahoy, K.L.; Knapp, M.; Morgan, R.E. CubeSats for Astronomy and Astrophysics. Submitted to the Astro 2020 Decadal Survey Call for APC Whitepapers. arXiv 2019, arXiv:1907.07634v2. [Google Scholar]
- Poghosyan, A.; Golkar, A. CubeSat evolution: Analyzing CubeSat capabilities for conducting science missions. Prog. Aerosp. Sci. 2017, 88, 59–83. [Google Scholar] [CrossRef]
- Han, K.; Wang, H.; Tu, B.; Jin, Z. Pico-Satellite Autonomous Navigation with Magnetometer and Sun Sensor Data. Chin. J. Aeronaut. 2011, 24, 46–54. [Google Scholar] [CrossRef] [Green Version]
- Kahr, E.; Montenbruck, O.; O’Keefe, K.; Skone, S.; Urbanek, J.; Bradbury, L.; Fenton, P. GPS tracking on a nanosatellite—The CanX-2 flight experience. In Proceedings of the 8th International ESA Conference on Guidance, Navigation & Control System, Karlovy Vary, Czech Republic, 5–10 June 2011. [Google Scholar]
- Lantto, S.; Gross, J.N. Precise Orbit Determination Using Duty Cycled GPS Observations. In Proceedings of the 2018 AIAA Modeling and Simulation Technologies Conference, AIAA SciTech Forum, Kissimmee, FL, USA, 8–12 January 2018; AIAA: Reston, VA, USA, 2018. [Google Scholar]
- Montenbruck, O.; Ramos-Bosch, P. Precision real-time navigation of LEO satellites using global positioning system measurements. GPS Solut. 2008, 12, 187–198. [Google Scholar] [CrossRef]
- Wesam, E.M.; Zhang, X.; Lu, Z.; Liao, W. Kalman filter implementation for small satellites using constraint GPS data. IOP Conf. Ser. Mater. Sci. Eng. 2017, 211, 012015. [Google Scholar] [CrossRef]
- Kahr, E.; Montenbruck, O.; O’Keefe, K.P.G. Estimation and analysis of two-line elements for small satellites. J. Spacecr. Rocket. 2013, 50, 433–439. [Google Scholar] [CrossRef] [Green Version]
- Bittner, D.E. Advances in MEMS IMU Cluster Technology for Small Satellite Applications. Graduate Theses, Dissertations, and Problem Reports, 5216. Master’s Thesis, The Benjamin M. Statler College of Engineering and Mineral Resources, West Virginia University, Morgantown, WV, USA, 2015. [Google Scholar]
- Morris, J.; Zemerick, S.; Grubb, M.; Lucas, J.; Jaridi, M.; Gross, J.N.; Christian, J.A.; Vassiliadis, D.; Kadiyala, A.; Dawson, J.; et al. Simulation-to-Flight 1 (STF-1): A mission to enable Cubesat software-based verification and validation. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems, 1st ed.; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 967–982. [Google Scholar]
- Noll, C.E. The Crustal Dynamics Data Information System: A resource to support scientific analysis using space geodesy. Adv. Space Res. 2010, 45, 1421–1440. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Han, C.; Chen, P. Precise real-time navigation of LEO satellites using a single-frequency GPS receiver and ultra-rapid ephemerides. Aerosp. Sci. Technol. 2017, 67, 228–236. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, A.B.; Masson, L.A.; Rossi, S.; Belloni, F.; Mullin, N.; Wiesendanger, R.; Rothacher, M.; Hollenstein, C.; Männel, B.; Willi, D.; et al. CUBETH: Nano-satellite mission for orbit and attitude determination using low-cost GNSS receivers. In Proceedings of the 66th International Astronautical Congress, IAC-15-B4.4.5, Jerusalem, Israel, 12–16 October 2015. [Google Scholar]
- Yang, Y.; Yue, X.; Tang, G.; Cui, H.; Song, B. Orbit Determination Using Combined GPS + Beidou Observations for Low Earth Cubesats: Software Validation in Ground Testbed. In China Satellite Navigation Conference (CSNC) 2015 Proceedings; Sun, J., Liu, J., Fan, S., Lu, X., Eds.; Part of the Lecture Notes in Electrical Engineering Book Series (Volume 342); Springer: Berlin/Heidelberg, Germany, 2015; Volume III, pp. 321–334. [Google Scholar]
- Hoque, M.M.; Jakowski, N. Ionospheric propagation effects on GNSS signals and new correction approaches. In Global Navigation Satellite Systems: Signal, Theory and Applications; Jin, S., Ed.; IntechOpen: Rijeka, Croatia, 2012; pp. 381–404. [Google Scholar]
- Mander, A.; Bisnach, S. GPS-based precise orbit determination of Low Earth Orbiters with limited resources. GPS Solut. 2013, 17, 587–594. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; University of Bern, Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar]
- Li, K.; Zhou, X.; Wang, W.; Gao, Y.; Zhao, G.; Tao, E.; Xu, K. Centimeter-Level Orbit Determination for TG02 Spacelab Using Onboard GNSS Data. Sensors 2018, 18, 2671. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beutler, G. Variational Equations. In Methods of Celestial Mechanics; Part of the Astronomy and Astrophysics Library Book Series; Springer: Berlin/Heidelberg, Germany, 2005; pp. 175–207. [Google Scholar]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods and Applications, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Jäggi, A.; Hugentobler, U.; Beutler, G. Pseudo-stochastic orbit modeling techniques for low Earth orbiters. J. Geod. 2006, 80, 47–60. [Google Scholar] [CrossRef] [Green Version]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. An Earth Gravitational Model to Degree 2160: EGM2008. In Proceedings of the European Geosciences Union General Assembly 2008, Vienna, Austria, 13–18 April 2008. [Google Scholar]
- Standish, E.M. JPL Planetary and Lunar Ephemerides, DE405/LE405, JPL IOM 312; F-98-048; JPL: Pasadena, CA, USA, 1998.
- Petit, G.; Luzum, B. IERS Conventions; IERS Technical Note No. 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010; 179p, ISBN 3-89888-989-6. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean. Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Flechtner, F.; Morton, P.; Watkins, M.; Webb, F. Status of the GRACE Follow-On Mission. In Gravity, Geoid and Height Systems; Marti, U., Ed.; Part of the International Association of Geodesy Symposia Book Series (Volume 141); Springer: Cham, Switzerland, 2014; pp. 117–121. [Google Scholar]
- Wen, H.Y.; Kruizinga, G.; Paik, M.; Landerer, F.; Bertiger, W.; Sakumura, C.; Bandikova, T.; Mccullough, C. Gravity Recovery and Climate Experiment Follow-On (GRACE-FO) Level-1 Data Product User Handbook. JPL D-56935 (URS270772), 11 September 2019. Available online: https://podaac-tools.jpl.nasa.gov/drive/files/allData/gracefo/docs/GRACE-FO_L1_Handbook.pdf (accessed on 26 May 2020).
- Hadas, T.; Bosy, J. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef] [Green Version]
- IGS Real-Time Service, Monitoring. Available online: http://www.igs.org/rts/monitor (accessed on 25 June 2020).
- IGC Products, Decoded Clock and Orbit Solutions from IGS Real-Time Product Streams; NASA Crustal Dynamics Data Information System (CDDIS): Greenbelt, MD, USA, 2018. Available online: http://cddis.nasa.gov/gnss/products/rtpp (accessed on 28 May 2020).
- Kazmierski, K.; Sośnica, K.; Hadas, T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning. GPS Solut. 2018, 22, 11. [Google Scholar] [CrossRef] [Green Version]
- The International GNSS Service. IGS Products. Available online: http://www.igs.org/products (accessed on 7 May 2020).
- Gatsonis, N.A.; Lu, Y.; Blandino, J.; Demetriou, M.A.; Paschalidis, N. Micro Pulsed Plasma Thrusters for Attitude Control of a Low Earth Orbiting CubeSat. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Henderson, D.M. Euler Angles, Quaternions, and Transformation Matrices for Space Shuttle Analysis; JSC Report 12960 (77-FM-37); NASA: Washington, DC, USA, 1977.














| Measurement Model | GPS code P1 + P2, phase L1 + L2 |
| IF linear combination | |
| Sampling interval: 10 s, 20 s, 30 s, 60 s, 120 s | |
| Elevation mask: 5°, 15°, 25° (for different mean satellite numbers) | |
| Arc length: 6 h, 12 h, 24 h | |
| GPS orbits and clocks: IGS final, rapid, real-time products | |
| Dynamic Model | Earth gravity: EGM2008 [39], Earth potential degree: 120 |
| N-body gravity: JPL DE405 [40] (Planetary ephemeris) | |
| Solid Earth tides: IERS Conventions 2010 | |
| Pole tides: IERS Conventions 2010 [41] | |
| Ocean tides: FES2004 [42] | |
| General relativistic term | |
| Reference Frame | IGS14, J2000.0 (Julian epoch) |
| Coordinate Transformation | Nutation and precession: IAU2000R06 [34] |
| Sub-daily pole variations: IERS Conventions 2010 [41] | |
| Earth rotation parameters: IGS final, rapid, ultra-rapid products |
| Elevation Mask [Degree] | Mean Integer Number of Satellites | Percentile of Valid SPP Solutions |
|---|---|---|
| 5 | 9 | 99.9% |
| 15 | 7 | 99.1% |
| 25 | 6 | 82.9% |
| Duty-Cycle/Mean # Satellite | 9 Satellites | 7 Satellites | 6 Satellites |
|---|---|---|---|
| 100% | -- | 1.1 | 2.1 |
| 80% | 1.6 | 1.9 | 2.4 |
| 60% | 2.0 | 2.1 | 2.7 |
| 40% | 2.6 | 2.9 | 3.5 |
| 20% | 3.5 | 3.9 | 4.8 |
| Orbits/Clocks | Identifier | Latency | Accuracy [cm] Orbit/Clock | Satellite Clock Sampling Interval [s] | 3D RMSE [cm] |
|---|---|---|---|---|---|
| IGS Final | IGS | 12–18 days | 2.5/2.25 | 30 | -- |
| IGS rapid | IGR | 17–41 h | 2.5/2.25 | 300 | 4.8 |
| IGS RTS | IGC | (Near)-real-time | 2–5/3–5 | 30 | 3.2 |
| Arc Length/Products | IGS Final [cm] | IGR [cm] | IGC [cm] |
|---|---|---|---|
| 24 h | -- | 4.8 | 3.2 |
| 12 h | 0.6 | 5.1 | 3.1 |
| 6 h | 1.0 | 5.6 | 3.5 |
| Duty-Cycle/Mean # Satellite Sampling Interval [s] | 8 Satellites 10/20/30/60/120 | 7 Satellites 10/20/30/60/120 | 5 Satellites 10/20/30/60/120 |
|---|---|---|---|
| 100% | 0.6/0.2/0.1/0.2/−0.1 | 0.1/0.1/0.2/0.2/0.2 | 0.1/0.0/0.1/0.1/0.2 |
| 80% | 0.2/0.1/0.5/0.4/−0.4 | 0.1/0.1/0.2/0.2/0.5 | 0.2/0.2/0.2/0.3/0.4 |
| 60% | 0.1/0.0/0.3/1.0/−0.4 | 0.1/0.1/0.2/0.2/0.5 | 0.0/0.1/0.1/0.1/1.0 |
| 40% | 0.2/0.3/0.3/0.6/0.8 | 0.2/0.0/0.2/0.7/1.7 | 0.2/0.3/0.5/2.0/3.5 |
| 20% | 2.0/2.2/2.8/3.3/-- | 1.6/2.2/3.0/3.6/-- | 2.9/2.0/3.4/4.8/-- |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Allahvirdi-Zadeh, A.; El-Mowafy, A.; Gross, J.N. A Sensitivity Study of POD Using Dual-Frequency GPS for CubeSats Data Limitation and Resources. Remote Sens. 2020, 12, 2107. https://doi.org/10.3390/rs12132107
Wang K, Allahvirdi-Zadeh A, El-Mowafy A, Gross JN. A Sensitivity Study of POD Using Dual-Frequency GPS for CubeSats Data Limitation and Resources. Remote Sensing. 2020; 12(13):2107. https://doi.org/10.3390/rs12132107
Chicago/Turabian StyleWang, Kan, Amir Allahvirdi-Zadeh, Ahmed El-Mowafy, and Jason N. Gross. 2020. "A Sensitivity Study of POD Using Dual-Frequency GPS for CubeSats Data Limitation and Resources" Remote Sensing 12, no. 13: 2107. https://doi.org/10.3390/rs12132107
APA StyleWang, K., Allahvirdi-Zadeh, A., El-Mowafy, A., & Gross, J. N. (2020). A Sensitivity Study of POD Using Dual-Frequency GPS for CubeSats Data Limitation and Resources. Remote Sensing, 12(13), 2107. https://doi.org/10.3390/rs12132107