A New and Simplified Approach for Estimating the Daily River Discharge of the Tibetan Plateau Using Satellite Precipitation: An Initial Study on the Upper Brahmaputra River
Abstract
:1. Introduction
2. Study Regions
3. Data and Method
3.1. Datasets
3.2. Methods
3.2.1. Basin-Averaged Precipitation
3.2.2. Exponential Filter
3.2.3. Linear Least-Squares Regression
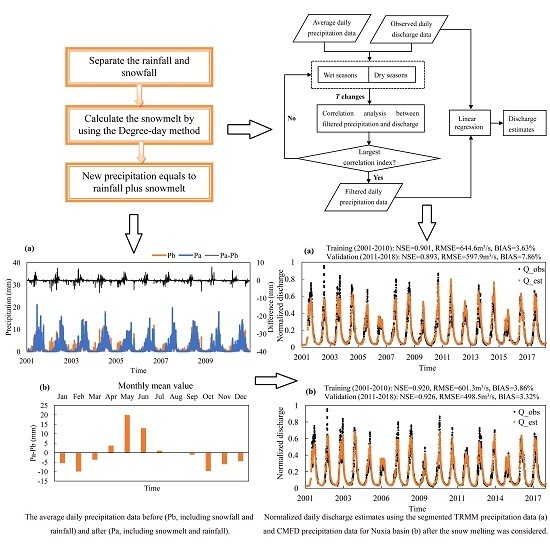
3.2.4. Segmented Processing of Precipitation Data
3.2.5. Calculation of Snowmelt
- (1)
- Separate the rainfall (Pr) and snowfall (Ps) from the daily precipitation data by using the method provided by Ding et al. [45];
- (2)
- Calculate the potential snowmelt capacity (SMc) by using the DDM;
- (3)
- If SMc > Ps, the actual snowmelt (SMa) is equal to the snowfall (that is SMa = Ps); otherwise SMa = SMc, and the value of Ps minus SMc is added to the Ps of the next day;
- (4)
- The daily active precipitation Pa is equal to the summation of Pr and SMa (Pa = Pr + SMa).
3.2.6. Performance Evaluation
3.2.7. Sensitivity Analysis of FLR
4. Method Evaluation
4.1. Results of Filtration
4.2. Performance of FLR in Discharge Estimation
4.3. How the Time Length of Training Data Series Influence FLR
4.4. Estimates of Historical Discharge Using Segmented CMFD Precipitation Data
4.5. Factors Impacting the Estimation Accuracy
4.6. The Impact of Snow Melting on the Discharge Estimation
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tarpanelli, A.; Amarnath, G.; Brocca, L.; Massari, C.; Moramarco, T. Discharge estimation and forecasting by MODIS and altimetry data in Niger-Benue River. Remote Sens. Environ. 2017, 195, 96–106. [Google Scholar] [CrossRef]
- Peterson, B.J.; Holmes, R.M.; McClelland, J.W.; Vorosmarty, C.J.; Lammers, R.B.; Shiklomanov, A.I.; Shiklomanov, I.A.; Rahmstorf, S. Increasing river discharge to the Arctic Ocean. Science 2002, 298, 2171–2173. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Koike, T.; Yang, K.; Yeh, P.J.F. Assessment of a distributed biosphere hydrological model against streamflow and MODIS land surface temperature in the upper Tone River Basin. J. Hydrol. 2009, 377, 21–34. [Google Scholar] [CrossRef]
- GRDC. River Discharge Data; GRDC: Koblenz, Germany, 2014. [Google Scholar]
- Wang, L.; Sichangi, A.; Zeng, T.; Li, X.; Hu, Z.; Genanu, M. New methods designed to estimate the daily discharges of rivers in the Tibetan Plateau. Sci. Bull. 2019, 64, 418–421. [Google Scholar] [CrossRef] [Green Version]
- Zhao, F.F.; Zongxue, X.U. Streamflow response to climate variability and human activities in the upper catchment of the Yellow River Basin. Sci. China 2009, 52, 3249–3256. [Google Scholar] [CrossRef]
- Qiu, J. China: The third pole. Nature 2008, 454, 393–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tong, K.; Su, F.G.; Yang, D.Q.; Hao, Z.C. Evaluation of satellite precipitation retrievals and their potential utilities in hydrologic modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Cuo, L.; Zhang, Y.X.; Gao, Y.H.; Hao, Z.C.; Cairang, L.S. The impacts of climate change and land cover/use transition on the hydrology in the upper Yellow River Basin, China. J. Hydrol. 2013, 502, 37–52. [Google Scholar] [CrossRef]
- Sun, W.C.; Ishidaira, H.; Bastola, S. Prospects for calibrating rainfall-runoff models using satellite observations of river hydraulic variables as surrogates for in situ river discharge measurements. Hydrol. Process. 2012, 26, 872–882. [Google Scholar] [CrossRef]
- Lauri, H.; de Moel, H.; Ward, P.J.; Rasanen, T.A.; Keskinen, M.; Kummu, M. Future changes in Mekong River hydrology: Impact of climate change and reservoir operation on discharge. Hydrol. Earth Syst. Sci. 2012, 16, 4603–4619. [Google Scholar] [CrossRef]
- Vilaysane, B.; Takara, K.; Luo, P.P.; Akkharath, I.; Duan, W.L. Hydrological stream flow modelling for calibration and uncertainty analysis using SWAT model in the Xedone river basin, Lao PDR. In 5th Sustainable Future for Human Security; Trihartono, A., McLellan, B., Eds.; Springer: Berlin, Germany, 2015; Volume 28, pp. 380–390. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Wang, L.; Zhou, H.; Yang, K.; Wang, A.; Li, W. Evaluation and application of a fine-resolution global data set in a semiarid mesoscale river basin with a distributed biosphere hydrological model. J. Geophys. Res. 2011, 116, D21108. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.G.; Mosbrugger, V.; Fan, Z.; Ma, Y.; Luo, T.; Xu, B.; Yang, X.; Joswiak, D.R.; Wang, W. Third Pole Environment (TPE). Environ. Dev. 2012, 3, 52–64. [Google Scholar] [CrossRef]
- Bookhagen, B.; Burbank, D.W. Toward a complete Himalayan hydrological budget: Spatiotemporal distribution of snowmelt and rainfall and their impact on river discharge. J. Geophys. Res. Earth Surf. 2010, 115, F03019. [Google Scholar] [CrossRef] [Green Version]
- Bjerklie, D.M.; Dingman, S.L.; Vorosmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the potential for measuring river discharge from space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Pan, F.; Wang, C.; Xi, X. Constructing river stage-discharge rating curves using remotely sensed river cross sectional inundation areas and river bathymetry. J. Hydrol. 2016, 540, 670–687. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Brocca, L.; Lacava, T.; Melone, F.; Moramarco, T.; Faruolo, M.; Pergola, N.; Tramutoli, V. Toward the estimation of river discharge variations using MODIS data in ungauged basins. Remote Sens. Environ. 2013, 136, 47–55. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Barbetta, S.; Brocca, L.; Moramarco, T. River Discharge Estimation by Using Altimetry Data and Simplified Flood Routing Modeling. Remote Sens. 2013, 5, 4145–4162. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.I.; Hong, Y.; Vergara, H.J.; Gourley, J.J.; Brakenridge, G.R.; De Groeve, T.; Flamig, Z.L.; Policelli, F.; Yong, B. Microwave Satellite Data for Hydrologic Modeling in Ungauged Basins. IEEE Geosci. Remote Sens. Lett. 2012, 9, 663–667. [Google Scholar] [CrossRef]
- Gleason, C.J.; Smith, L.C. Toward global mapping of river discharge using satellite images and at-many-stations hydraulic geometry. Proc. Natl. Acad. Sci. USA 2014, 111, 4788–4791. [Google Scholar] [CrossRef] [Green Version]
- Jarihani, A.A.; Callow, J.N.; Johansen, K.; Gouweleeuw, B. Evaluation of multiple satellite altimetry data for studying inland water bodies and river floods. J. Hydrol. 2013, 505, 78–90. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Moller, D.; Smith, L.C.; Dingman, S.L. Estimating discharge in rivers using remotely sensed hydraulic information. J. Hydrol. 2005, 309, 191–209. [Google Scholar] [CrossRef]
- LeFavour, G.; Alsdorf, D. Water slope and discharge in the Amazon River estimated using the shuttle radar topography mission digital elevation model. Geophys. Res. Lett. 2005, 32, 5. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Long, D.; Du, M.D.; Zeng, C.; Qiao, G.; Li, X.D.; Hou, A.Z.; Hong, Y. Discharge estimation in high-mountain regions with improved methods using multisource remote sensing: A case study of the Upper Brahmaputra River. Remote Sens. Environ. 2018, 219, 115–134. [Google Scholar] [CrossRef]
- Sichangi, A.W.; Wang, L.; Yang, K.; Chen, D.L.; Wang, Z.J.; Li, X.P.; Zhou, J.; Liu, W.B.; Kuria, D. Estimating continental river basin discharges using multiple remote sensing data sets. Remote Sens. Environ. 2016, 179, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Temimi, M.; Lacava, T.; Lakhankar, T.; Tramutoli, V.; Ghedira, H.; Ata, R.; Khanbilvardi, R. A multi-temporal analysis of AMSR-E data for flood and discharge monitoring during the 2008 flood in Iowa. Hydrol. Process. 2011, 25, 2623–2634. [Google Scholar] [CrossRef] [Green Version]
- Ling, F.; Cai, X.B.; Li, W.B.; Xiao, F.; Li, X.D.; Du, Y. Monitoring river discharge with remotely sensed imagery using river island area as an indicator. J. Appl. Remote Sens. 2012, 6, 14. [Google Scholar] [CrossRef]
- Sichangi, A.W.; Wang, L.; Hu, Z.D. Estimation of River Discharge Solely from Remote-Sensing Derived Data: An Initial Study over the Yangtze River. Remote Sens. 2018, 10, 1385. [Google Scholar] [CrossRef] [Green Version]
- Pavelsky, T.M. Using width- based rating curves from spatially discontinuous satellite imagery to monitor river discharge. Hydrol. Process. 2014, 28, 3035–3040. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; Moore, P.; Kilsby, C.G.; O′Donnell, G.M.; Hardy, A.J.; Berry, P.A.M. Daily discharge estimation at ungauged river sites using remote sensing. Hydrol. Process. 2014, 28, 1043–1054. [Google Scholar] [CrossRef]
- Tourian, M.J.; Schwatke, C.; Sneeuw, N. River discharge estimation at daily resolution from satellite altimetry over an entire river basin. J. Hydrol. 2017, 546, 230–247. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beek, L.P.H.; Bierkens, M.F.P. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- You, Q.L.; Kang, S.C.; Wu, Y.H.; Yan, Y.P. Climate change over the yarlung zangbo river basin during 1961–2005. J. Geogr. Sci. 2007, 17, 409–420. [Google Scholar] [CrossRef]
- Zhang, L.; Su, F.; Yang, D.; Hao, Z.; Tong, K. Discharge regime and simulation for the upstream of major rivers over Tibetan Plateau. J. Geophys. Res. Atmos. 2013, 118, 8500–8518. [Google Scholar] [CrossRef]
- Iwadra, M.; Odirile, P.T.; Parida, B.P.; Moalafhi, D.B. Evaluation of future climate using SDSM and secondary data (TRMM and NCEP) for poorly gauged catchments of Uganda: The case of Aswa catchment. Theor. Appl. Climatol. 2019, 137, 2029–2048. [Google Scholar] [CrossRef]
- Munzimi, Y.A.; Hansen, M.C.; Asante, K.O. Estimating daily streamflow in the Congo Basin using satellite-derived data and a semi-distributed hydrological model. Hydrol. Sci. J. 2019, 64, 1472–1487. [Google Scholar] [CrossRef]
- Xie, Z.; Hu, Z.; Gu, L.; Sun, G.; Du, Y.; Yan, X. Meteorological Forcing Datasets for Blowing Snow Modeling on the Tibetan Plateau: Evaluation and Intercomparison. J. Hydrometeorol. 2017, 18, 2761–2780. [Google Scholar] [CrossRef]
- Yang, F.; Lu, H.; Yang, K.; He, J.; Wang, W.; Wright, J.S.; Li, C.; Han, M.; Li, Y. Evaluation of multiple forcing data sets for precipitation and shortwave radiation over major land areas of China. Hydrol. Earth Syst. Sci. 2017, 21, 5805–5821. [Google Scholar] [CrossRef] [Green Version]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Tropical Rainfall Measuring Mission (TRMM). TRMM (TMPA) Rainfall Estimate L3 3 Hour 0.25-Degree x 0.25 Degree V7; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2011. [Google Scholar] [CrossRef]
- He, J.; Yang, K. China Meteorological Forcing Dataset; Cold and Arid Regions Science Data Center: Lanzhou, China, 2001. [Google Scholar] [CrossRef]
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 12, 1323–1337. [Google Scholar] [CrossRef] [Green Version]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Ding, B.; Yang, K.; Qin, J.; Wang, L.; Chen, Y.; He, X. The dependence of precipitation types on surface elevation and meteorological conditions and its parameterization. J. Hydrol. 2014, 513, 154–163. [Google Scholar] [CrossRef]
- Finsterwalder, S.; Schunk, H. Der Suldenferner. Z. Dtsch. Oesterreichischen Alp. 1887, 18, 72–89. [Google Scholar]
- Liu, J.; Zhang, W. Spatial variability in degree-day factors in Yarlung Zangbo River Basin in China. J. Univ. Chin. Acad. Sci. 2018, 35, 704–711. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D.; Dercas, N.; Londra, P.A. Investigation of the direct runoff generation mechanism for the analysis of the SCS-CN method applicability to a partial area experimental watershed. Hydrol. Earth Syst. Sci. 2009, 13, 605–615. [Google Scholar] [CrossRef] [Green Version]
- Rezaei-Sadr, H. Influence of coarse soils with high hydraulic conductivity on the applicability of the SCS-CN method. Hydrol. Sci. J. 2017, 62, 843–848. [Google Scholar] [CrossRef]
- Hawkins, R.H. Runoff curve numbers for partial area watersheds. J. Irrig. Drain. Div. ASCE 1979, 105, 375–389. [Google Scholar]












| Station Name | Basin Area above the Station (km2) | Glacier Area in the Basin above the Station (km2) | Areal Proportion of Glaciers (%) |
|---|---|---|---|
| Yangcun | 156,561 | 1793 | 1.14 |
| Nuxia | 195,766 | 3183 | 1.63 |
| Time for Training | Training | Validation (2011–2018) | Validation (2001–2018) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NSE | RMSE (m3/s) | BIAS (%) | NSE | RMSE (m3/s) | BIAS (%) | NSE | RMSE (m3/s) | BIAS (%) | |
| 2003 | 0.930 | 673.7 | 3.70 | 0.750 | 914.6 | 20.6 | 0.792 | 913.2 | 18.3 |
| 2004 | 0.953 | 488.1 | 2.59 | 0.870 | 659.1 | 8.25 | 0.879 | 696.5 | 4.44 |
| 2005 | 0.882 | 569.0 | 3.44 | 0.911 | 546.6 | 4.89 | 0.897 | 642.9 | 2.07 |
| 2006 | 0.941 | 272.8 | 1.72 | 0.913 | 540.6 | 5.16 | 0.863 | 740.5 | 1.64 |
| 2007 | 0.900 | 695.7 | 5.02 | 0.847 | 715.1 | 20.7 | 0.867 | 728.5 | 15.7 |
| 2008 | 0.955 | 482.5 | 2.44 | 0.874 | 648.5 | 16.2 | 0.878 | 697.5 | 11.1 |
| 2009 | 0.933 | 294.9 | 3.6 | 0.844 | 721.7 | 4.41 | 0.780 | 938.0 | 1.60 |
| 2010 | 0.919 | 633.6 | 1.71 | 0.907 | 556.2 | −3.98 | 0.890 | 662.2 | −7.2 |
| 2001–2005 | 0.901 | 726.9 | 3.89 | 0.844 | 722.0 | 12.3 | 0.866 | 731.6 | 9.36 |
| 2002–2006 | 0.904 | 641.3 | 3.33 | 0.863 | 676.7 | 9.93 | 0.876 | 705.6 | 6.87 |
| 2003–2007 | 0.900 | 645.2 | 4.22 | 0.876 | 642.8 | 11.4 | 0.887 | 673.1 | 7.83 |
| 2004–2008 | 0.917 | 567.2 | 3.42 | 0.891 | 602.7 | 11.0 | 0.892 | 657.0 | 6.98 |
| 2005–2009 | 0.899 | 564.4 | 3.89 | 0.904 | 566.7 | 11.5 | 0.893 | 655.4 | 7.37 |
| 2006–2010 | 0.909 | 572.7 | 4.19 | 0.905 | 564.5 | 9.78 | 0.892 | 658.3 | 5.62 |
| 2001–2010 | 0.894 | 691.6 | 4.41 | 0.889 | 608.8 | 11.1 | 0.893 | 655.6 | 7.41 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, T.; Wang, L.; Li, X.; Song, L.; Zhang, X.; Zhou, J.; Gao, B.; Liu, R. A New and Simplified Approach for Estimating the Daily River Discharge of the Tibetan Plateau Using Satellite Precipitation: An Initial Study on the Upper Brahmaputra River. Remote Sens. 2020, 12, 2103. https://doi.org/10.3390/rs12132103
Zeng T, Wang L, Li X, Song L, Zhang X, Zhou J, Gao B, Liu R. A New and Simplified Approach for Estimating the Daily River Discharge of the Tibetan Plateau Using Satellite Precipitation: An Initial Study on the Upper Brahmaputra River. Remote Sensing. 2020; 12(13):2103. https://doi.org/10.3390/rs12132103
Chicago/Turabian StyleZeng, Tian, Lei Wang, Xiuping Li, Lei Song, Xiaotao Zhang, Jing Zhou, Bing Gao, and Ruishun Liu. 2020. "A New and Simplified Approach for Estimating the Daily River Discharge of the Tibetan Plateau Using Satellite Precipitation: An Initial Study on the Upper Brahmaputra River" Remote Sensing 12, no. 13: 2103. https://doi.org/10.3390/rs12132103
APA StyleZeng, T., Wang, L., Li, X., Song, L., Zhang, X., Zhou, J., Gao, B., & Liu, R. (2020). A New and Simplified Approach for Estimating the Daily River Discharge of the Tibetan Plateau Using Satellite Precipitation: An Initial Study on the Upper Brahmaputra River. Remote Sensing, 12(13), 2103. https://doi.org/10.3390/rs12132103