Investigating Live Fuel Moisture Content Estimation in Fire-Prone Shrubland from Remote Sensing Using Empirical Modelling and RTM Simulations
Abstract
:1. Introduction
2. Methods
2.1. Study Area and Reference Data
2.2. Remote Sensing Data
2.2.1. Image Selection and Preprocessing
2.2.2. Spectral Indices
2.3. Empirical Methods
2.4. Radiative Transfer Model (RTM) Simulations
3. Results
3.1. LFMC Variability and Remote Sensing Data
3.2. Comparison between Reflectance Source and Statistical Method
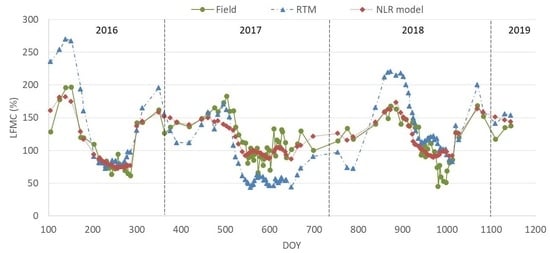
3.3. RTM Simulations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Example of Outlier Detection in Spectral Indices Described in Section 3.1

Appendix B. Examples of Spectral Reflectance Profiles Derived from Sentinel-2 and Both MCD43A4 and MOD09GA MODIS Products

References
- Chuvieco, E.; Gonzalez, I.; Verdú, F.; Aguado, I.; Yebra, M. Prediction of fire occurrence from live fuel moisture content measurements in a Mediterranean ecosystem. Int. J. Wildland Fire 2009, 18, 430. [Google Scholar] [CrossRef]
- Dennison, P.E.; Moritz, M.A. Critical live fuel moisture in chaparral ecosystems: A threshold for fire activity and its relationship to antecedent precipitation. Int. J. Wildland Fire 2009, 18, 1021–1027. [Google Scholar] [CrossRef]
- Weise, D.R.; Zhou, X.; Sun, L.; Mahalingam, S. Fire spread in chaparral- ‘go or no go?’. Int. J. Wildland Fire 2005, 14, 99–106. [Google Scholar] [CrossRef]
- Marino, E.; Dupuy, J.L.; Pimont, F.; Guijarro, M.; Hernando, C.; Linn, R. Fuel bulk density and fuel moisture content effect on fire rate of spread: A comparison between FIRETEC model predictions and experimental results in shrub fuels. J. Fire Sci. 2012, 30, 277–299. [Google Scholar] [CrossRef]
- Rossa, C.G.; Veloso, R.; Fernandes, P.M. A laboratory-based quantification of the effect of live fuel moisture content on fire spread rate. Int. J. Wildland Fire 2016, 25, 569–573. [Google Scholar] [CrossRef] [Green Version]
- Agee, J.K.; Wright, C.S.; Williamson, N.; Huff, M.H. Foliar moisture content of Pacific Northwest vegetation and its relation to wildland fire behavior. Forest Ecol. Manag. 2002, 167, 57–66. [Google Scholar] [CrossRef]
- Alexander, M.E.; Cruz, M.G. Assessing the effect of foliar moisture content on the spread rate of crown fires. Int. J. Wildland Fire 2013, 22, 415–427. [Google Scholar] [CrossRef]
- Ruffault, J.; Curt, T.; Martin-StPaul, N.K.; Moron, V.; Trigo, R.M. Extreme wildfire events are linked to global-change-type droughts in the northern Mediterranean. Nat. Hazards Earth Syst. Sci. 2018, 18, 847–856. [Google Scholar] [CrossRef] [Green Version]
- Spinosi, J.; Barbosa, P.; Bucchgnai, E.; Cassano, J.; Cavazos, T.; Christensen, J.H.; Christensen, O.B.; Coppola, E.; Evans, J.; Giorgi, F.; et al. Future Global Meteorological Drought Hot Spots: A Study Based on CORDEX Data. J. Clim. 2020, 33, 3635–3661. [Google Scholar] [CrossRef]
- Moreira, F.; Viedma, O.; Arianoutsou, M.; Curt, T.; Koutsias, N.; Rigolot, E.; Barbati, A.; Corona, P.; Vaz, P.; Xanthopoulos, G.; et al. Landscape–wildfire interactions in southern Europe: Implications for landscape management. J. Environ. Manag. 2011, 92, 2389–2402. [Google Scholar] [CrossRef] [Green Version]
- Pausas, J.G.; Fernández-Muñoz, S. Fire regime changes in the Western Mediterranean Basin: From fuel-limited to drought-driven fire regime. Clim. Chang. 2012, 10, 215–226. [Google Scholar] [CrossRef] [Green Version]
- Linn, R.; Reisner, J.; Colman, J.J.; Winterkamp, J. Studying wildfire behavior using FIRETEC. Int. J. Wildland Fire 2002, 11, 233–246. [Google Scholar] [CrossRef]
- Finney, M.A. FARSITE: Fire Area Simulator–Model Development and Evaluation. In USDA Forest Service, Rocky Mountain Research Station; Research Paper RMRS-RP-4 Revised: Fort Collins, CO, USA, 2004. [Google Scholar]
- Finney, M.A. An overview of FlamMap fire modelling capabilities. In Proceedings of the ‘Fuels Management–How to Measure Success: Conference Proceedings’, Portland, OR, USA, 28–30 March 2006; Andrews, P.L., Butler, B.W., Eds.; USDA Forest Service, Rocky Mountain Research Station, Proceedings RMRS-P 41: Fort Collins, CO, USA, 2006; pp. 213–220. [Google Scholar]
- García, M.; Riaño, D.; Yebra, M.; Salas, J.; Cardil, A.; Monedero, S.; Ramirez, J.; Martín, M.P.; Vilar, L.; Gajardo, J.; et al. A Live Fuel Moisture Content Product from Landsat TM Satellite Time Series for Implementation in Fire Behavior Models. Remote Sens. 2020, 12, 1714. [Google Scholar] [CrossRef]
- Chuvieco, E.; Aguado, I.; Salas JGarcia, M.; Yebra, M.; Oliva, P. Satellite Remote Sensing Contributions to Wildland Fire Science and Management. Curr. For. Rep. 2020, 6, 81–96. [Google Scholar] [CrossRef]
- Martin-StPaul, N.; Pimont, F.; Dupuy, J.L.; Rigolot, E.; Ruffault, J.; Fargeon, H.; Cabane, E.; Duché, Y.; Savazzi, R.; Toutchkov, M. Live fuel moisture content (LFMC) time series for multiple sites and species in the French Mediterranean area since 1996. Ann. For. Sci. 2018, 75, 57. [Google Scholar] [CrossRef] [Green Version]
- Yebra, M.; Scortechini, G.; Badi, A.; Beget, M.E.; Boer, M.M.; Bradstock, R.; Chuvieco, E.; Danson, F.M.; Dennison, P.; de Dios, V.R.; et al. Globe-LFMC, a global plant water status database for vegetation ecophysiology and wildfire applications. Nat. Sci. Data 2019, 6, 155. [Google Scholar] [CrossRef] [Green Version]
- Yebra, M.; Dennison, P.E.; Chuvieco, E.; Riaño, D.; Zylstra, P.; Hunt ERJr Danson, F.M.; Qi, Y.; Jurdao, S. A global review of remote sensing of live fuel moisture content for fire danger assessment: Moving towards operational products. Remote Sens. Environ. 2013, 136, 455–468. [Google Scholar] [CrossRef]
- Dennison, P.E.; Roberts, D.A.; Peterson, S.H.; Rechel, J. Use of Normalized Difference Water Index for monitoring live fuel moisture. Int. J. Remote Sens. 2005, 26, 1035–1042. [Google Scholar] [CrossRef]
- Stow, D.; Madhura, N.; Kaiser, J. Time series of chaparral live fuel moisture maps derived from MODIS satellite data. Int. J. Wildland Fire 2006, 15, 347–360. [Google Scholar] [CrossRef]
- Peterson, S.; Roberts, D.A.; Dennison, P.E. Mapping live fuel moisture with MODIS data: A multiple regression approach. Remote Sens. Environ. 2008, 112, 4272–4284. [Google Scholar] [CrossRef]
- Caccamo, G.; Chisholm, L.A.; Bradstock, R.A.; Puotinen, M.L.; Pippen, B.G. Monitoring live fuel moisture content of heathland, shrubland and sclerophyll forest in south-eastern Australia using MODIS data. Int. J. Wildland Fire 2012, 21, 257–269. [Google Scholar] [CrossRef]
- Shu, Q.; Quan, X.; Yebra, M.; Liu, X.; Wang, L.; Zhang, Y. Evaluating the Sentinel-2A satellite data for fuel moisture content retrieval. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 9416–9419. [Google Scholar]
- Tanase, M.A.; Panciera, R.; Lowell, K.; Aponte, C. Monitoring live fuel moisture in semiarid environments using L-band radar data. Int. J. Wildland Fire 2015, 24, 560–572. [Google Scholar] [CrossRef]
- Fan, L.; Wigneron, J.P.; Xiao, Q.; Al-Yaari, A.; Wen, J.; Martin-St Paul, N.; Dupuy, J.L.; Pimont, F.; Al Bitar, A.; Fernandez-Moran, R.; et al. Evaluation of microwave remote sensing for monitoring live fuel moisture content in the Mediterranean region. Remote Sens. Environ. 2018, 205, 210–223. [Google Scholar] [CrossRef]
- Wang, L.; Quan, X.; He, B.; Yebra, M.; Xing, M.; Liu, X. Assessment of the dual polarimetric Sentinel-1A data for forest fuel moisture content estimation. Remote Sens. 2019, 11, 1568. [Google Scholar] [CrossRef] [Green Version]
- Hao, X.J.; Qu, J.J. Retrieval of real-time live fuel moisture content using MODIS measurements. Remote Sens. Environ. 2007, 108, 130–137. [Google Scholar] [CrossRef]
- Yebra, M.; Chuvieco, E.; Riaño, D. Estimation of live Fuel Moisture Content from MODIS images for fire risk assessment. Agric. For. Meteorol. 2008, 148, 523–536. [Google Scholar] [CrossRef]
- Yebra, M.; Chuvieco, E. Linking ecological information and radiative transfer models to estimate fuel moisture content in the Mediterranean region of Spain: Solving the ill-posed inverse problem. Remote Sens. Environ. 2009, 113, 2403–2411. [Google Scholar] [CrossRef]
- Jurdao, S.; Yebra, M.; Guerschman, J.P.; Chuvieco, E. Regional estimation of woodland moisture content by inverting Radiative Transfer Models. Remote Sens. Environ. 2013, 132, 59–70. [Google Scholar] [CrossRef]
- Fosberg, M.A.; Deeming, J.E. Derivation of the 1- and 10-hour Timelag Fuel Moisture Calculation for Fire Danger Rating. In USDA Forest Service, Rocky Mountain Forest and Range Experiment Station; Research Paper RM-207; Rocky Mountain Forest and Range Experiment Station: Fort Collins, CO, USA, 1971; 10p. [Google Scholar]
- Louis, J.; Debaecker, V.; Pflug, B.; Main-Knorn, M.; Bieniarz, J.; Mueller-Wilm, U.; Cadau, E.; Gascon, F. Sentinel-2 Sen2Cor: L2A Processor for Users. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; Ouwehand, L.L., Ed.; ESA-SP: São Paulo, Brazil, 2016; p. 91, ISBN 978-92-9221-305-3. [Google Scholar]
- Rouse, J.W., Jr.; Haas, R.W.; Schell, J.A.; Deering, D.H.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Greenwave Effect) of Natural Vegetation; Type III Final Report; NASA/GSFC: Greenbelt, MD, USA, 1974.
- Hardisky, M.A.; Klemas, V.; Smart, R.M. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of Spartina alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 49, 77–83. [Google Scholar]
- Ceccato, P.; Flasse, S.; Gregoire, J.M. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 2. Validation and applications. Remote Sens. Environ. 2002, 82, 198–207. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI. A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Gitelson, A.; Kaufmam, J.Y.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef] [Green Version]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; URL: R Foundation for Statistical Computing: Vienna, Austria, 2016. Available online: https://www.gbif.org/tool/81287/r-a-language-and-environment-for-statistical-computing (accessed on 10 July 2020).
- Yebra, M.; Quan, X.; Riaño, D.; Rozas, P.; van Dijk, A.; Cary, J.K. A fuel moisture content and flammability monitoring methodology for continental Australia based on optical remote sensing. Remote Sens. Environ. 2018, 212, 260–272. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Kuusk, A. The Hot Spot Effect in Plant Canopy Reflectance. In Photon-Vegetation Interactions; Myneni, R., Ross, J., Eds.; Springer: Berli/Heidelberg, Germany, 1991; pp. 139–159. [Google Scholar]
- Jurdao, S.; Yebra, M.; Chuvieco, E. Live Fuel Moisture Content Derived from Remote Sensing Estimates in Temperate Shrublands and Grasslands. In Earthzine; IEEE Oceanic Engineering Society, 2013; Available online: https://earthzine.org/live-fuel-moisture-content-derived-from-remote-sensing-estimates-in-temperate-shrublands-and-grasslands/ (accessed on 24 October 2013).
- Adab, H.; Kanniah, K.D.; Beringer, J. Estimating and up-scaling fuel moisture and leaf dry matter content of a temperate humid forest using multi resolution remote sensing data. Remote Sens. 2016, 8, 961. [Google Scholar] [CrossRef] [Green Version]
- Pivovaroff, A.L.; Emery, N.; Sharifi, M.R.; Witter, M.; Keeley, J.E.; Rundel, P.W. The effect of ecophysiological traits on live fuel moisture content. Fire 2019, 2, 28. [Google Scholar] [CrossRef] [Green Version]
- Garcia, M.; Chuvieco, E.; Nieto, H.; Aguado, I. Combining AVHRR and meteorological data for estimating live fuel moisture content. Remote Sens. Environ. 2008, 112, 3618–3627. [Google Scholar] [CrossRef]
- Nolan, R.H.; Resco de Dios, V.; Boer, M.M.; Caccamo, G.; Goulden, M.L.; Bradstock, R.A. Predicting dead fine fuel moisture at regional scales using vapour pressure deficit from MODIS and gridded weather data. Remote Sens. Environ. 2016, 174, 100–108. [Google Scholar] [CrossRef] [Green Version]






| Index | Formulation | MODIS Bands | Sentinel-2 Bands | Refer. |
|---|---|---|---|---|
| Normalized Difference Vegetation Index | [34] | |||
| Normalized Difference Infrared Index | (NDII6) (NDII7) | [35] | ||
| Global Vegetation Moisture Index | [36] | |||
| Normalized Difference Water Index | n.a. | [37] | ||
| Normalized Difference Red-Edge Index | n.a. | |||
| Enhanced Vegetation Index | [38] | |||
| Soil Adjusted Vegetation Index | [39] | |||
| Visible Atmospherically Resistant Index | [40] | |||
| Vegetation Index—Green | [41] |
| Image | Calibration | Validation | ||
|---|---|---|---|---|
| n | LFMC Range (%) | n | LFMC Range (%) | |
| MCD43A4 | 80 | 50–197 | 40 | 45–196 |
| MOD09GA | 65 | 50–196 | 32 | 61–195 |
| Sentinel-2 | 47 | 50–183 | 24 | 63–160 |
| Product | SI | LFMC | NDVI | NDII6 | NDII7 | GVMI | NDWI | EVI | SAVI | VARI |
|---|---|---|---|---|---|---|---|---|---|---|
| MCD43A4 | NDVI | 0.844 | ||||||||
| NDII6 | 0.461 | 0.578 | ||||||||
| NDII7 | 0.590 | 0.730 | 0.647 | |||||||
| GVMI | 0.678 | 0.852 | 0.640 | 0.918 | ||||||
| NDWI | 0.671 | 0.751 | 0.619 | 0.854 | 0.804 | |||||
| EVI | 0.712 | 0.799 | 0.660 | 0.775 | 0.742 | 0.875 | ||||
| SAVI | 0.728 | 0.816 | 0.654 | 0.758 | 0.736 | 0.868 | 0.999 | |||
| VARI | 0.846 | 0.961 | 0.616 | 0.718 | 0.838 | 0.735 | 0.803 | 0.815 | ||
| VIgreen | 0.843 | 0.961 | 0.622 | 0.729 | 0.846 | 0.741 | 0.807 | 0.817 | 1.000 | |
| MOD09GA | NDVI | 0.761 | ||||||||
| NDII6 | 0.630 | 0.633 | ||||||||
| NDII7 | 0.566 | 0.581 | 0.949 | |||||||
| GVMI | 0.630 | 0.633 | 1.000 | 0.949 | ||||||
| NDWI | 0.596 | 0.477 | 0.699 | 0.711 | 0.699 | |||||
| EVI | 0.714 | 0.506 | 0.683 | 0.639 | 0.683 | 0.677 | ||||
| SAVI | 0.761 | 1.000 | 0.633 | 0.581 | 0.633 | 0.477 | 0.506 | |||
| VARI | 0.866 | 0.738 | 0.682 | 0.592 | 0.682 | 0.673 | 0.793 | 0.738 | ||
| VIgreen | 0.859 | 0.724 | 0.689 | 0.597 | 0.689 | 0.681 | 0.794 | 0.724 | 0.999 |
| SI | LFMC | NDVI | NDII | NDI45 | GVMI | EVI | SAVI | VARI |
|---|---|---|---|---|---|---|---|---|
| NDVI | 0.428 ** | |||||||
| NDII | 0.445 ** | 0.311 * | ||||||
| NDI45 | 0.382 ** | 0.959 *** | 0.274 | |||||
| GVMI | 0.159 | 0.307 ** | 0.225 | 0.166 | ||||
| EVI | 0.523 *** | 0.338 * | 0.385 ** | 0.396 ** | 0.338 ** | |||
| SAVI | 0.458 ** | 0.708 *** | 0.178 | 0.743 *** | 0.013 | 0.729 *** | ||
| VARI | 0.637 *** | 0.456 ** | 0.825 *** | 0.408 ** | 0.233 * | 0.407 ** | 0.239 | |
| VIgreen | 0.624 *** | 0.432 ** | 0.815 *** | 0.375 ** | 0.251 * | 0.392 ** | 0.221 | 0.995 *** |
| Sensor/MODIS Product | Model | Formulation | Parameters | p-value | Calibration | Validation | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 adj | RMSE (%) | MAE (%) | R2 adj | RMSE (%) | MAE (%) | |||||
| MCD43A4 | LR | FMC = a+b·VARI | a = 152.676 b = 487.731 | < 0.0001 < 0.0001 | 0.711 | 17.87 | 14.14 | 0.756 | 17.29 | 12.32 |
| MLR | FMC = a+b· VIgreen +c·GVMI+d·NDWI | a = 198.73 b = 715.49 c = −149.33 d = 234.32 | < 0.0001 < 0.0001 0.0556 0.0534 | 0.718 | 17.54 | 13.88 | 0.782 | 16.31 | 12.12 | |
| NLR | FMC = a+b·log(1+VARI)+c·log(NDVI) | a = 203.5 b = 253.5 c = 88.61 | < 0.0001 0.0195 0.0441 | 0.729 | 17.20 | 13.58 | 0.752 | 17.36 | 12.05 | |
| GAMs | FMC = f(a,s(VARI),s(NDVI)) | a = 111.23 s(VARI) s(NDVI) | < 0.0001 < 0.0001 0.0012 | 0.781 | 15.05 | 11.91 | 0.750 | 16.54 | 12.47 | |
| MOD09GA | LR | FMC = a+b·VARI | a = 153.352 b = 430.273 | < 0.0001 < 0.0001 | 0.750 | 15.46 | 12.96 | 0.696 | 17.01 | 14.52 |
| MLR | FMC = a+b·VARI+c·NDVI | a = 96.18 b = 331.77 c = 101.37 | < 0.0001 < 0.0001 0.0032 | 0.783 | 14.41 | 11.83 | 0.721 | 16.24 | 13.35 | |
| NLR | FMC = a+b·log(1+VARI)+c·log(NDVI) | a = 178.00 b = 325.36 c = 42.07 | < 0.0001 < 0.0001 0.0034 | 0.780 | 14.30 | 11.66 | 0.720 | 15.96 | 13.39 | |
| GAMs | FMC = f(a,s(VARI),s(NDVI)) | a = 111.65 s(VARI) s(NDVI) | < 0.0001 < 0.0001 0.0157 | 0.784 | 13.98 | 11.47 | 0.686 | 15.99 | 13.33 | |
| Sentinel-2 | LR | FMC = a+bVARI | a = 136.320 b = 372.929 | < 0.0001 < 0.0001 | 0.393 | 22.84 | 17.33 | 0.702 | 14.73 | 12.69 |
| MLR | FMC = a+b·VARI+c·SAVI | a = 60.57 b = 333.05 c = 390.22 | 0.0242 < 0.0001 0.0048 | 0.482 | 20.85 | 15.77 | 0.732 | 13.65 | 11.21 | |
| NLR | FMC = a+b·log(1+VARI)+c·log(SAVI) | a = 244.53 b = 327.81 c = 65.41 | < 0.0001 < 0.0001 0.0075 | 0.473 | 20.81 | 15.46 | 0.737 | 13.54 | 11.11 | |
| GAMs | FMC = f(a,s(VARI),s(SAVI)) | a = 113.88 s(VARI) s(SAVI) | < 0.0001 0.0002 0.0031 | 0.586 | 17.63 | 13.33 | 0.695 | 13.58 | 11.06 | |
| Dataset | RTM | NLR Model (Validation Dataset) | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (%) | MAE (%) | n | R2 | RMSE (%) | MAE (%) | n | |
| Total | 0.489 | 39.44 | 31.55 | 116 | 0.752 | 17.36 | 12.05 | 40 |
| 2016 | 0.848 | 37.52 | 25.02 | 30 | 0.938 | 10.74 | 7.47 | 10 |
| 2017 | 0.711 | 43.44 | 38.07 | 43 | 0.79 | 16.24 | 12.03 | 14 |
| 2018 * | 0.562 | 36.43 | 29.58 | 43 | 0.647 | 21.22 | 14.92 | 16 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marino, E.; Yebra, M.; Guillén-Climent, M.; Algeet, N.; Tomé, J.L.; Madrigal, J.; Guijarro, M.; Hernando, C. Investigating Live Fuel Moisture Content Estimation in Fire-Prone Shrubland from Remote Sensing Using Empirical Modelling and RTM Simulations. Remote Sens. 2020, 12, 2251. https://doi.org/10.3390/rs12142251
Marino E, Yebra M, Guillén-Climent M, Algeet N, Tomé JL, Madrigal J, Guijarro M, Hernando C. Investigating Live Fuel Moisture Content Estimation in Fire-Prone Shrubland from Remote Sensing Using Empirical Modelling and RTM Simulations. Remote Sensing. 2020; 12(14):2251. https://doi.org/10.3390/rs12142251
Chicago/Turabian StyleMarino, Eva, Marta Yebra, Mariluz Guillén-Climent, Nur Algeet, José Luis Tomé, Javier Madrigal, Mercedes Guijarro, and Carmen Hernando. 2020. "Investigating Live Fuel Moisture Content Estimation in Fire-Prone Shrubland from Remote Sensing Using Empirical Modelling and RTM Simulations" Remote Sensing 12, no. 14: 2251. https://doi.org/10.3390/rs12142251
APA StyleMarino, E., Yebra, M., Guillén-Climent, M., Algeet, N., Tomé, J. L., Madrigal, J., Guijarro, M., & Hernando, C. (2020). Investigating Live Fuel Moisture Content Estimation in Fire-Prone Shrubland from Remote Sensing Using Empirical Modelling and RTM Simulations. Remote Sensing, 12(14), 2251. https://doi.org/10.3390/rs12142251