A Simple Algorithm for Deriving an NDVI-Based Index Compatible between GEO and LEO Sensors: Capabilities and Limitations in Japan
Abstract
:1. Introduction
2. Test Site and Data
2.1. Test Site
2.2. Satellite Data
2.3. Geographic Coordinates and Illumination and View Angles
3. Algorithm for Computing the NDVI-Based Index
3.1. NDVI-Isoline-Based LMM Including Atmospheric Effects
3.2. Automated Computation of the Pseudo-Endmember Spectra
4. Data Processing and Comparison Methods
4.1. Processing Steps Used to Prepare the AHI and MODIS Scene Pairs
- Search near-nadir MODIS data: MODIS scenes that included a point , where and are the latitude and longitude and i identifies the region, designated in Table 1, were explored. The scenes that satisfied the following two conditions were obtained: View zenith angle of the point () was equal to or less than 10 degrees, and the area around the target region was not influenced by clouds, cirrus clouds, or snow observed by visual inspection.
- Extract an area of at most 300-by-300 km of MODIS data: If the MODIS data satisfying the above condition were found, a 300-by-300 pixel area around the center point or largest possible rectangular area that did not exceed 300 pixels on any side around was extracted. Subsequently, pixels in the data that exceeded 10 degrees of the viewing zenith angle were masked.
- Extract a target area from the MODIS: A target area in the MODIS, selected to be as extensive as possible, was manually extracted from the 300-by-300 km data or the largest possible area of data. The shape of the area was a parallelogram that included more than 1000 non-water body pixels and did not contain cloud or snow. This was accomplished by visual inspection rather than by using cloud and snow flags, as this process almost completely avoided the effects of cloud contamination, including cirrus clouds and snow cover. The target area was selected to include water bodies, as discussed in Section 3.2.
- Extract the AHI target area and create a scene pair: The AHI scene observed at the time closest to the MODIS observation time was selected, and the AHI partial scene corresponding to the MODIS target area was extracted to create a MODIS and AHI partial scene pair for comparison.
4.2. Comparison Method
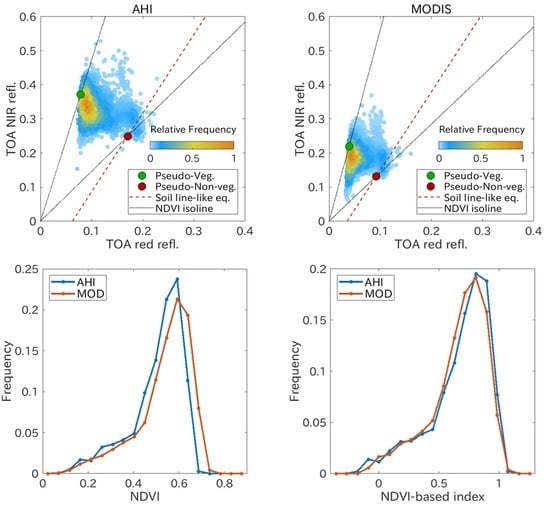
5. Results
5.1. Scene-by-Scene Comparison
5.2. Pixel-by-Pixel Comparison
6. Discussion
6.1. Differences between the Sensor-Specific NDVI/NDVI-Based Indices
6.2. Comparison with Previous Studies
6.3. Characteristics in the Developed Algorithm
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GEO | Geostationary |
| LEO | Low earth orbit |
| SRF | Spectral response function |
| NDVI | Normalized Difference Vegetation Index |
| LMM | Linear mixture model |
| FVC | Fraction of vegetation cover |
| AHI | Advanced Himawari Imager |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MSG | Meteosat Second Generation |
| SEVIRI | Spinning Enhanced Visible and Infrared Imager |
| BRDF | Bidirectional Reflectance Distribution Function |
| GOCI | Geostationary Ocean Color Imager |
| TOA | Top-of-atmosphere |
| BOA | Bottom-of-atmosphere |
| ROI | Region of interest |
| IGBP | International Geosphere-Biosphere Programme |
| SAVI | Soil Adjusted Vegetation Index |
Appendix A. Approximation of the FVC Using the TOA Reflectances
References
- Zhang, Y.; Song, C.; Band, L.E.; Sun, G.; Li, J. Reanalysis of global terrestrial vegetation trends from MODIS products: Browning or greening? Remote Sens. Environ. 2017, 191, 145–155. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.P.; Huang, C.; Channan, S.; Baker, M.E.; Townshend, J.R. Urban growth of the Washington, D.C.–Baltimore, MD metropolitan region from 1984 to 2010 by annual, Landsat-based estimates of impervious cover. Remote Sens. Environ. 2013, 129, 42–53. [Google Scholar] [CrossRef]
- Claessen, J.; Molini, A.; Martens, B.; Detto, M.; Demuzere, M.; Miralles, D.G. Global biosphere–climate interaction: A causal appraisal of observations and models over multiple temporal scales. Biogeosciences 2019, 16, 4851–4874. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Stisen, S.; Tucker, C. Analysing NDVI for the African continent using the geostationary meteosat second generation SEVIRI sensor. Remote Sens. Environ. 2006, 101, 212–229. [Google Scholar] [CrossRef]
- Guan, K.; Medvigy, D.; Wood, E.F.; Caylor, K.K.; Li, S.; Jeong, S. Deriving Vegetation Phenological Time and Trajectory Information Over Africa Using SEVIRI Daily LAI. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1113–1130. [Google Scholar] [CrossRef]
- Barbosa, H.A.; Lakshmi Kumar, T.; Paredes, F.; Elliott, S.; Ayuga, J. Assessment of Caatinga response to drought using Meteosat-SEVIRI Normalized Difference Vegetation Index (2008–2016). ISPRS J. Photogramm. Remote Sens. 2019, 148, 235–252. [Google Scholar] [CrossRef]
- García-Haro, F.J.; Camacho, F.; Martínez, B.; Campos-Taberner, M.; Fuster, B.; Sánchez-Zapero, J.; Gilabert, M.A. Climate Data Records of Vegetation Variables from Geostationary SEVIRI/MSG Data: Products, Algorithms and Applications. Remote Sens. 2019, 11, 2103. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An Introduction to Himawari-8/9 Japan’s New-Generation Geostationary Meteorological Satellites. J. Meteorol. Soc. Japan Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Schmit, T.J.; Griffith, P.; Gunshor, M.M.; Daniels, J.M.; Goodman, S.J.; Lebair, W.J. A Closer Look at the ABI on the GOES-R Series. Bull. Am. Meteorol. Soc. 2017, 98, 681–698. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Z.; Wei, C.; Lu, F.; Guo, Q. Introducing the New Generation of Chinese Geostationary Weather Satellites, Fengyun-4. Bull. Am. Meteorol. Soc. 2017, 98, 1637–1658. [Google Scholar] [CrossRef]
- EUMETSAT. METEOSAT Third Generation. Available online: https://www.eumetsat.int/website/home/Satellites/FutureSatellites/MeteosatThirdGeneration/index.html (accessed on 13 February 2020).
- Miura, T.; Nagai, S.; Takeuchi, M.; Ichii, K.; Yoshioka, H. Improved Characterisation of Vegetation and Land Surface Seasonal Dynamics in Central Japan with Himawari-8 Hypertemporal Data. Sci. Rep. 2019, 9, 15692. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Huete, A.; Tran, N.N.; Bi, J.; Gao, S.; Zeng, Y. Sun-Angle Effects on Remote-Sensing Phenology Observed and Modelled Using Himawari-8. Remote Sens. 2020, 12, 1339. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, K.; Chen, C.; Bai, T.; Park, T.; Wang, W.; Nemani, R.R.; Myneni, R.B. Generation and Evaluation of LAI and FPAR Products from Himawari-8 Advanced Himawari Imager (AHI) Data. Remote Sens. 2019, 11, 1517. [Google Scholar] [CrossRef]
- Li, S.; Wang, W.; Hashimoto, H.; Xiong, J.; Vandal, T.; Yao, J.; Qian, L.; Ichii, K.; Lyapustin, A.; Wang, Y.; et al. First Provisional Land Surface Reflectance Product from Geostationary Satellite Himawari-8 AHI. Remote Sens. 2019, 11, 2990. [Google Scholar] [CrossRef]
- He, T.; Zhang, Y.; Liang, S.; Yu, Y.; Wang, D. Developing Land Surface Directional Reflectance and Albedo Products from Geostationary GOES-R and Himawari Data: Theoretical Basis, Operational Implementation, and Validation. Remote Sens. 2019, 11, 2655. [Google Scholar] [CrossRef]
- Wang, W.; Li, S.; Hashimoto, H.; Takenaka, H.; Higuchi, A.; Kalluri, S.; Nemani, R. An Introduction to the Geostationary-NASA Earth Exchange (GeoNEX) Products: 1. Top-of-Atmosphere Reflectance and Brightness Temperature. Remote Sens. 2020, 12, 1267. [Google Scholar] [CrossRef]
- Seong, N.H.; Jung, D.; Kim, J.; Han, K.S. Evaluation of NDVI Estimation Considering Atmospheric and BRDF Correction through Himawari-8/AHI. Asia-Pac. J. Atmos. Sci. 2020, 56, 265–274. [Google Scholar] [CrossRef]
- Klein, C.; Bliefernicht, J.; Heinzeller, D.; Gessner, U.; Klein, I.; Kunstmann, H. Feedback of observed interannual vegetation change: A regional climate model analysis for the West African monsoon. Clym. Dyn. 2017, 48, 2837–2858. [Google Scholar] [CrossRef]
- Adachi, Y.; Kikuchi, R.; Obata, K.; Yoshioka, H. Relative Azimuthal-Angle Matching (RAM): A Screening Method for GEO-LEO Reflectance Comparison in Middle Latitude Forests. Remote Sens. 2019, 11, 1095. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Proud, S.R.; Stisen, S.; Rasmussen, M.O. Assessment of MODIS sun-sensor geometry variations effect on observed NDVI using MSG SEVIRI geostationary data. Int. J. Remote Sens. 2010, 31, 6163–6187. [Google Scholar] [CrossRef]
- Proud, S.R.; Zhang, Q.; Schaaf, C.; Fensholt, R.; Rasmussen, M.O.; Shisanya, C.; Mutero, W.; Mbow, C.; Anyamba, A.; Pak, E.; et al. The Normalization of Surface Anisotropy Effects Present in SEVIRI Reflectances by Using the MODIS BRDF Method. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6026–6039. [Google Scholar] [CrossRef]
- Yeom, J.M.; Kim, H.O. Comparison of NDVIs from GOCI and MODIS Data towards Improved Assessment of Crop Temporal Dynamics in the Case of Paddy Rice. Remote Sens. 2015, 7, 11326–11343. [Google Scholar] [CrossRef]
- Yeom, J.M.; Jeong, S.; Jeong, G.; Ng, C.T.; Deo, R.C.; Ko, J. Monitoring paddy productivity in North Korea employing geostationary satellite images integrated with GRAMI-rice model. Sci. Rep. 2018, 8, 16121. [Google Scholar] [CrossRef] [PubMed]
- Yan, D.; Zhang, X.; Nagai, S.; Yu, Y.; Akitsu, T.; Nasahara, K.N.; Ide, R.; Maeda, T. Evaluating land surface phenology from the Advanced Himawari Imager using observations from MODIS and the Phenological Eyes Network. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 71–83. [Google Scholar] [CrossRef]
- Wanner, W.; Li, X.; Strahler, A.H. On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res. Atmos. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Trishchenko, A.P.; Cihlar, J.; Li, Z. Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors. Remote Sens. Environ. 2002, 81, 1–18. [Google Scholar] [CrossRef]
- Trishchenko, A.P. Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors: Extension to AVHRR NOAA-17, 18 and METOP-A. Remote Sens. Environ. 2009, 113, 335–341. [Google Scholar] [CrossRef]
- Qin, Y.; McVicar, T.R. Spectral band unification and inter-calibration of Himawari AHI with MODIS and VIIRS: Constructing virtual dual-view remote sensors from geostationary and low-Earth-orbiting sensors. Remote Sens. Environ. 2018, 209, 540–550. [Google Scholar] [CrossRef]
- Fan, X.; Liu, Y. Multisensor Normalized Difference Vegetation Index Intercalibration: A Comprehensive Overview of the Causes of and Solutions for Multisensor Differences. IEEE Geosci. Remote Sens. Mag. 2018, 6, 23–45. [Google Scholar] [CrossRef]
- Gao, L.; Wang, X.; Johnson, B.A.; Tian, Q.; Wang, Y.; Verrelst, J.; Mu, X.; Gu, X. Remote sensing algorithms for estimation of fractional vegetation cover using pure vegetation index values: A review. ISPRS J. Photogramm. Remote Sens. 2020, 159, 364–377. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modeling: A new analysis of rock and soil types at the Viking Lander 1 Site. J. Geophys. Res. Solid Earth Planets 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
- Verstraete, M.; Pinty, B. The potential contribution of satellite remote-sensing to the understanding of arid lands processes. In Vegetation and Climate Interactions in Semi-Arid Regions; Henderson-Sellers, A., Pitman, A., Eds.; Springer: Dordrecht, The Netherlands, 1991; pp. 59–72. [Google Scholar]
- Wittich, K.P.; Hansing, O. Area-averaged vegetative cover fraction estimated from satellite data. Int. J. Biometeorol. 1995, 38, 209–215. [Google Scholar] [CrossRef]
- Obata, K.; Yoshioka, H. Inter-Algorithm Relationships for the Estimation of the Fraction of Vegetation Cover Based on a Two Endmember Linear Mixture Model with the VI Constraint. Remote Sens. 2010, 2, 1680–1701. [Google Scholar] [CrossRef]
- Liu, J.; Melloh, R.A.; Woodcock, C.E.; Davis, R.E.; Ochs, E.S. The effect of viewing geometry and topography on viewable gap fractions through forest canopies. Hydrol. Process. 2004, 18, 3595–3607. [Google Scholar] [CrossRef]
- Liu, J.; Woodcock, C.E.; Melloh, R.A.; Davis, R.E.; McKenzie, C.; Painter, T.H. Modeling the View Angle Dependence of Gap Fractions in Forest Canopies: Implications for Mapping Fractional Snow Cover Using Optical Remote Sensing. J. Hydrometeorol. 2008, 9, 1005–1019. [Google Scholar] [CrossRef]
- Song, W.; Mu, X.; Ruan, G.; Gao, Z.; Li, L.; Yan, G. Estimating fractional vegetation cover and the vegetation index of bare soil and highly dense vegetation with a physically based method. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 168–176. [Google Scholar] [CrossRef]
- Tong, X.; Liu, T.; Singh, V.P.; Duan, L.; Long, D. Development of In Situ Experiments for Evaluation of Anisotropic Reflectance Effect on Spectral Mixture Analysis for Vegetation Cover. IEEE Geosci. Remote Sens. Lett. 2016, 13, 636–640. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Friedl, M. User Guide to Collection 6 MODIS Land Cover (MCD12Q1 and MCD12C1) Product; Technical Report; LP DAAC, the USG Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2018. Available online: https://lpdaac.usgs.gov/documents/101/MCD12_User_Guide_V6.pdf (accessed on 17 February 2020).
- Sulla-Menashe, D.; Gray, J.M.; Abercrombie, S.P.; Friedl, M.A. Hierarchical mapping of annual global land cover 2001 to present: The MODIS Collection 6 Land Cover product. Remote Sens. Environ. 2019, 222, 183–194. [Google Scholar] [CrossRef]
- Bell, D.G.; Kuehnel, F.; Maxwell, C.; Kim, R.; Kasraie, K.; Gaskins, T.; Hogan, P.; Coughlan, J. NASA World Wind: Opensource GIS for Mission Operations. In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; pp. 1–9. [Google Scholar]
- MODIS Characterization Support Team (MCST). MODIS 1 km Calibrated Radiances Product; Technical Report; NASA MODIS Adaptive Processing System, Goddard Space Flight Center: Greenbelt, MD, USA, 2018. Available online: https://modaps.modaps.eosdis.nasa.gov/services/about/products/c61/MOD021KM.html (accessed on 14 February 2020).
- MODIS Characterization Support Team (MCST). MODIS Geolocation Fields Product; Technical Report; NASA MODIS Adaptive Processing System, Goddard Space Flight Center: Greenbelt, MD, USA, 2018.
- Li, Z.; Cihlar, J.; Zheng, X.; Moreau, L.; Ly, H. The bidirectional effects of AVHRR measurements over boreal regions. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1308–1322. [Google Scholar]
- Bacour, C.; Bréon, F.M. Variability of biome reflectance directional signatures as seen by POLDER. Remote Sens. Environ. 2005, 98, 80–95. [Google Scholar] [CrossRef]
- Huber, S.; Tagesson, T.; Fensholt, R. An automated field spectrometer system for studying VIS, NIR and SWIR anisotropy for semi-arid savanna. Remote Sens. Environ. 2014, 152, 547–556. [Google Scholar] [CrossRef]
- EUMETSAT. Coordination Group for Meteorological Satellites (CGMS) LRIT/HRIT Global Specification. Available online: https://www.cgms-info.org/documents/cgms-lrit-hrit-globalspecification-(v2-8-of-30-oct-2013).pdf (accessed on 26 May 2020).
- Danielson, J.; Gesch, D. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010); Technical Report; U.S. Geological Survey: Sioux Falls, SD, USA, 2011.
- Rino, C. Full Vectorization of Solar Azimuth and Elevation Estimation. MATLAB Central File Exchange. 2020. Available online: https://www.mathworks.com/matlabcentral/fileexchange/48594-full-vectorization-of-solar-azimuth-and-elevation-estimation (accessed on 26 May 2020).
- Soler, T.; Eisemann, D.W. Determination of Look Angles to Geostationary Communication Satellites. J. Surv. Eng. 1994, 120, 115–127. [Google Scholar] [CrossRef]
- Zeng, X.; Dickinson, R.E.; Walker, A.; Shaikh, M.; DeFries, R.S.; Qi, J. Derivation and Evaluation of Global 1-km Fractional Vegetation Cover Data for Land Modeling. J. Appl. Meteorol. 2000, 39, 826–839. [Google Scholar] [CrossRef]
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Baret, F.; Jacquemoud, S.; Hanocq, J.F. The soil line concept in remote sensing. Remote Sens. Rev. 1993, 7, 65–82. [Google Scholar] [CrossRef]
- Ahmadian, N.; Demattê, J.A.M.; Xu, D.; Borg, E.; Zölitz, R. A New Concept of Soil Line Retrieval from Landsat 8 Images for Estimating Plant Biophysical Parameters. Remote Sens. 2016, 8, 738. [Google Scholar] [CrossRef]
- Koenker, R.W.; Bassett, G. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K.F. Quantile Regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Xu, D.; Guo, X. A Study of Soil Line Simulation from Landsat Images in Mixed Grassland. Remote Sens. 2013, 5, 4533–4550. [Google Scholar] [CrossRef]
- Malik, N.; Bookhagen, B.; Mucha, P.J. Spatiotemporal patterns and trends of Indian monsoonal rainfall extremes. Geophys. Res. Lett. 2016, 43, 1710–1717. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Ichii, K.; Higuchi, A.; Takenaka, H. Geolocation Accuracy Assessment of Himawari-8/AHI Imagery for Application to Terrestrial Monitoring. Remote Sens. 2020, 12, 1372. [Google Scholar] [CrossRef]
- Robert, E.W. MODIS Geolocation. In Earth Science Satellite Remote Sensing Volume 1: Science and Instruments; Qu, J., Gao, W., Kafatos, M., Murphy, R., Salomonson, V., Eds.; Springer: Berlin, Germany, 2006; pp. 50–73. [Google Scholar]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmara, H.; Pacholcyzk, P.; Smets, B. GEOV1: LAI and FAPAR essential climate variables and FCOVER global time series capitalizing over existing products. Part 1: Principles of development and production. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Yeom, J.M.; Kim, H.O. Feasibility of using Geostationary Ocean Colour Imager (GOCI) data for land applications after atmospheric correction and bidirectional reflectance distribution function modelling. Int. J. Remote Sens. 2013, 34, 7329–7339. [Google Scholar] [CrossRef]
- Miura, T.; Yoshioka, H.; Fujiwara, K.; Yamamoto, H. Inter-Comparison of ASTER and MODIS Surface Reflectance and Vegetation Index Products for Synergistic Applications to Natural Resource Monitoring. Sensors 2008, 8, 2480–2499. [Google Scholar] [CrossRef] [PubMed]
- Yoshioka, H.; Miura, T.; Obata, K. Derivation of Relationships between Spectral Vegetation Indices from Multiple Sensors Based on Vegetation Isolines. Remote Sens. 2012, 4, 583–597. [Google Scholar] [CrossRef]
- Taniguchi, K.; Obata, K.; Yoshioka, H. Analytical Relationship between Two-Band Spectral Vegetation Indices Measured at Multiple Sensors on a Parametric Representation of Soil Isoline Equations. Remote Sens. 2019, 11, 1620. [Google Scholar] [CrossRef]
- Yoshioka, H. Vegetation isoline equations for an atmosphere-canopy-soil system. IEEE Trans. Geosci. Remote Sens. 2004, 42, 166–175. [Google Scholar] [CrossRef]
- Mousivand, A.; Verhoef, W.; Menenti, M.; Gorte, B. Modeling Top of Atmosphere Radiance over Heterogeneous Non-Lambertian Rugged Terrain. Remote Sens. 2015, 7, 8019–8044. [Google Scholar] [CrossRef]












| Hokkaido | Tohoku | Tokai | Shikoku | Kyushu | |
|---|---|---|---|---|---|
| Latitude | 43 | 38.29 | 35.12 | 33.69 | 33.28 |
| Longitude | 141.38 | 140.83 | 137.38 | 133.49 | 130.34 |
| AHI view zenith angle | 49.6 | 44.3 | 40.9 | 39.9 | 40.3 |
| AHI view azimuth angle | 181.0 | 180.2 | 174.2 | 167.1 | 161.6 |
| Hokkaido | Tohoku | Tokai | Shikoku | Kyushu | |
|---|---|---|---|---|---|
| Date and | 16 July 2015, 0340 | 27 October 2015, 0345 | 19 December 2015, 0405 | 28 September 2015, 0415 | 31 July 2015, 0435 |
| MODIS hhmm | 8 May 2016, 0335 | 5 November 2015, 0340 | 17 March 2016, 0400 | 14 October 2015, 0415 | 3 October 2015, 0435 |
| 12 August 2016, 0335 | 15 May 2016, 0340 | 4 May 2016, 0400 | 21 October 2015, 0420 | 19 October 2015, 0435 | |
| 2 May 2017, 0340 | 22 May 2016, 0345 | 7 July 2016, 0355 | 1 December 2015, 0415 | 4 November 2015, 0435 | |
| 18 May 2017, 0340 | 7 November 2016, 0340 | 31 August 2016, 0405 | 8 December 2015, 0420 | 16 January 2016, 0430 | |
| 12 Jun 2017, 0335 | 18 May 2017, 0340 | 12 November 2016, 0355 | 10 February 2016, 0420 | 23 May 2016, 0430 | |
| 14 July 2017, 0335 | 10 November 2017, 0340 | 30 December 2016, 0355 | 22 March 2016, 0415 | 30 May 2016, 0435 | |
| 21 May 2018, 0340 | 3 December 2017, 0345 | 31 January 2017, 0355 | 19 December 2016, 0415 | 19 February 2017, 0430 | |
| 6 Jun 2018, 0340 | 20 January 2018, 0345 | 11 March 2017, 0405 | 21 February 2017, 0415 | 2 Jun 2017, 0435 | |
| 24 July 2018, 0340 | 19 April 2018, 0340 | 28 April 2017, 0405 | 19 May 2017, 0420 | 18 Jun 2017, 0435 | |
| - | 26 April 2018, 0345 | 26 February 2018, 0405 | 4 Jun 2017, 0420 | 27 December 2017, 0435 | |
| - | 4 November 2018, 0345 | 14 March 2018, 0405 | 24 February 2018, 0415 | 27 April 2018, 0430 | |
| - | - | 30 March 2018, 0405 | 13 April 2018, 0415 | - | |
| - | - | 8 October 2018, 0405 | 29 April 2018, 0415 | - | |
| - | - | - | 13 October 2018, 0420 | - | |
| - | - | - | 29 October 2018, 0420 | - | |
| AHI hhmm | 0340 | 0340 | 0400 | 0420 | 0430 |
| (%) | (%) | (%) | (Degree) | () |
|---|---|---|---|---|
| 95 | 1 | 5 | 0.04 |
| Date | N | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 16 July 2015 | 1033 | 28 | 0.581 | −0.0232 | 0.608 | 0.00569 | 1 | 0 | 0.772 | 0.779 |
| 8 May 2016 | 3601 | 32.5 | 0.378 | −0.0205 | 0.454 | 0.00467 | 1 | 0 | 0.746 | 0.768 |
| 12 August 2016 | 1582 | 33.8 | 0.609 | −0.0228 | 0.464 | −0.0417 | 1 | 1 | 0.728 | 0.719 |
| 2 May 2017 | 1645 | 34 | 0.312 | −0.0236 | 0.435 | 0.00914 | 1 | 0 | 0.854 | 0.862 |
| 18 May 2017 | 1433 | 30.5 | 0.473 | −0.0141 | 0.486 | −0.00294 | 1 | 0 | 0.71 | 0.696 |
| 12 Jun 2017 | 5873 | 27 | 0.664 | −0.0253 | 0.652 | −0.00767 | 1 | 0 | 0.865 | 0.866 |
| 14 July 2017 | 4034 | 27.9 | 0.589 | −0.0359 | 0.474 | −0.0945 | 1 | 1 | 0.842 | 0.82 |
| 21 May 2018 | 2240 | 30 | 0.497 | −0.0189 | 0.581 | 0.00289 | 1 | 0 | 0.714 | 0.719 |
| 6 Jun 2018 | 1678 | 27.8 | 0.565 | −0.0227 | 0.559 | −0.0013 | 1 | 0 | 0.779 | 0.778 |
| 24 July 2018 | 1105 | 29.3 | 0.548 | −0.0276 | 0.556 | −0.00488 | 1 | 0 | 0.657 | 0.659 |
| Date | N | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 19 December 2015 | 4533 | 62.1 | 0.505 | −0.0303 | 0.676 | 0.00934 | 1 | 1 | 0.918 | 0.916 |
| 17 March 2016 | 5890 | 40.6 | 0.442 | −0.0234 | 0.613 | −0.00708 | 1 | 0 | 0.952 | 0.95 |
| 4 May 2016 | 8115 | 27.6 | 0.584 | −0.0214 | 0.722 | −0.0111 | 1 | 1 | 0.903 | 0.905 |
| 7 July 2016 | 2100 | 22.3 | 0.588 | −0.0107 | 0.689 | 0.00401 | 1 | 0 | 0.886 | 0.882 |
| 31 August 2016 | 1466 | 33 | 0.543 | −0.015 | 0.633 | −0.00812 | 1 | 0 | 0.927 | 0.93 |
| 12 November 2016 | 9066 | 57.8 | 0.519 | −0.0278 | 0.686 | 0.0113 | 1 | 1 | 0.932 | 0.932 |
| 30 December 2016 | 5275 | 61.5 | 0.52 | −0.0229 | 0.687 | 0.0172 | 1 | 1 | 0.92 | 0.918 |
| 31 January 2017 | 3918 | 55.3 | 0.405 | −0.0249 | 0.557 | −0.00347 | 1 | 0 | 0.943 | 0.942 |
| 11 March 2017 | 2478 | 42.8 | 0.525 | −0.019 | 0.706 | −0.000809 | 1 | 0 | 0.873 | 0.874 |
| 28 April 2017 | 1166 | 28.8 | 0.458 | −0.0122 | 0.525 | −0.0121 | 1 | 0 | 0.908 | 0.917 |
| 26 February 2018 | 6728 | 47.3 | 0.414 | −0.0174 | 0.563 | −0.00262 | 1 | 0 | 0.952 | 0.953 |
| 14 March 2018 | 7712 | 41.8 | 0.415 | −0.0128 | 0.577 | −0.00396 | 1 | 0 | 0.961 | 0.961 |
| 30 March 2018 | 13749 | 36.3 | 0.452 | −0.0117 | 0.613 | −0.00394 | 1 | 0 | 0.928 | 0.929 |
| 8 October 2018 | 4298 | 46.4 | 0.497 | −0.024 | 0.592 | −0.00904 | 1 | 0 | 0.946 | 0.948 |
| Date | N | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 27 October 2015 | 13802 | 55.3 | 0.508 | −0.0364 | 0.67 | 0.0134 | 1 | 1 | 0.843 | 0.843 |
| 5 November 2015 | 17776 | 58.6 | 0.447 | −0.0285 | 0.667 | 0.0313 | 1 | 1 | 0.823 | 0.826 |
| 15 May 2016 | 6691 | 26.7 | 0.547 | −0.0248 | 0.602 | −0.0187 | 1 | 1 | 0.853 | 0.855 |
| 22 May 2016 | 8180 | 25.7 | 0.542 | −0.0328 | 0.591 | −0.00602 | 1 | 1 | 0.896 | 0.897 |
| 7 November 2016 | 9021 | 59.2 | 0.433 | −0.0238 | 0.664 | 0.0113 | 1 | 1 | 0.809 | 0.812 |
| 18 May 2017 | 3363 | 26.1 | 0.59 | −0.021 | 0.652 | 0.0207 | 1 | 1 | 0.866 | 0.87 |
| 10 November 2017 | 6563 | 59.9 | 0.43 | −0.0288 | 0.645 | 0.00181 | 1 | 1 | 0.856 | 0.844 |
| 3 December 2017 | 3422 | 63.9 | 0.377 | −0.0247 | 0.626 | 0.00669 | 1 | 1 | 0.882 | 0.84 |
| 20 January 2018 | 2339 | 60.7 | 0.394 | −0.0203 | 0.579 | −0.0047 | 1 | 0 | 0.889 | 0.896 |
| 19 April 2018 | 7848 | 33 | 0.411 | −0.0152 | 0.61 | −0.00875 | 1 | 0 | 0.898 | 0.886 |
| 26 April 2018 | 5287 | 31.2 | 0.456 | −0.0184 | 0.574 | 0.00475 | 1 | 0 | 0.893 | 0.89 |
| 4 November 2018 | 4067 | 57.8 | 0.49 | −0.0314 | 0.674 | 0.0084 | 1 | 1 | 0.752 | 0.75 |
| Date | N | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 28 September 2015 | 4030 | 41.9 | 0.638 | −0.0272 | 0.777 | 0.00706 | 1 | 1 | 0.715 | 0.709 |
| 14 October 2015 | 6969 | 47.6 | 0.619 | −0.0227 | 0.765 | 0.0168 | 1 | 1 | 0.796 | 0.797 |
| 21 October 2015 | 6034 | 49.7 | 0.591 | −0.0287 | 0.801 | 0.02 | 1 | 1 | 0.766 | 0.765 |
| 1 December 2015 | 1898 | 59.5 | 0.582 | −0.0206 | 0.777 | 0.0232 | 1 | 1 | 0.76 | 0.761 |
| 8 December 2015 | 2886 | 60 | 0.612 | −0.0265 | 0.656 | −0.0053 | 1 | 0 | 0.634 | 0.648 |
| 10 February 2016 | 7814 | 50.9 | 0.586 | −0.0174 | 0.725 | 0.0163 | 1 | 1 | 0.712 | 0.731 |
| 22 March 2016 | 13658 | 37.6 | 0.558 | −0.0189 | 0.722 | 0.00808 | 1 | 1 | 0.818 | 0.822 |
| 19 December 2016 | 13150 | 60.7 | 0.536 | −0.0145 | 0.707 | 0.0245 | 1 | 1 | 0.809 | 0.818 |
| 21 February 2017 | 2940 | 47.2 | 0.594 | −0.0207 | 0.796 | 0.0169 | 1 | 1 | 0.793 | 0.804 |
| 19 May 2017 | 6053 | 23.5 | 0.688 | −0.0194 | 0.79 | −0.0366 | 1 | 1 | 0.683 | 0.687 |
| 4 Jun 2017 | 1744 | 21.4 | 0.679 | −0.0156 | 0.796 | −0.0227 | 1 | 1 | 0.766 | 0.757 |
| 24 February 2018 | 2264 | 46.6 | 0.57 | −0.0151 | 0.787 | 0.0137 | 1 | 1 | 0.855 | 0.852 |
| 13 April 2018 | 9956 | 31.3 | 0.562 | −0.0181 | 0.749 | −0.00479 | 1 | 0 | 0.83 | 0.83 |
| 29 April 2018 | 7586 | 27.5 | 0.625 | −0.019 | 0.786 | 0.00392 | 1 | 0 | 0.777 | 0.778 |
| 13 October 2018 | 1559 | 47.1 | 0.668 | −0.0266 | 0.738 | −0.00446 | 1 | 0 | 0.659 | 0.689 |
| 29 October 2018 | 1211 | 52.1 | 0.671 | −0.0277 | 0.698 | −0.0226 | 1 | 1 | 0.515 | 0.516 |
| Date | N | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 31 July 2015 | 1172 | 23.8 | 0.634 | −0.00304 | 0.675 | 0.00426 | 1 | 0 | 0.938 | 0.937 |
| 3 October 2015 | 2883 | 43.3 | 0.621 | −0.0221 | 0.711 | −0.0107 | 1 | 0 | 0.916 | 0.911 |
| 19 October 2015 | 4611 | 48.9 | 0.579 | −0.0248 | 0.707 | −0.00463 | 1 | 0 | 0.856 | 0.865 |
| 4 November 2015 | 3613 | 53.9 | 0.527 | −0.0251 | 0.671 | 0.00924 | 1 | 1 | 0.836 | 0.847 |
| 16 January 2016 | 8706 | 57.5 | 0.451 | −0.0125 | 0.646 | 0.00295 | 1 | 1 | 0.841 | 0.841 |
| 23 May 2016 | 16654 | 23.9 | 0.625 | −0.02 | 0.716 | −0.0087 | 1 | 1 | 0.861 | 0.862 |
| 30 May 2016 | 4808 | 22.4 | 0.579 | −0.0244 | 0.671 | −0.0136 | 1 | 1 | 0.806 | 0.801 |
| 19 February 2017 | 16264 | 48 | 0.494 | −0.0116 | 0.649 | 0.00363 | 1 | 1 | 0.846 | 0.847 |
| 2 Jun 2017 | 5111 | 22.2 | 0.593 | −0.0147 | 0.699 | −0.00344 | 1 | 1 | 0.856 | 0.859 |
| 18 Jun 2017 | 1008 | 21.3 | 0.419 | 0.000215 | 0.42 | 0.023 | 0 | 0 | 0.816 | 0.817 |
| 27 December 2017 | 4373 | 59.9 | 0.491 | −0.0224 | 0.661 | −0.00439 | 1 | 0 | 0.911 | 0.913 |
| 27 April 2018 | 1483 | 28 | 0.546 | −0.00759 | 0.574 | 0.0108 | 1 | 0 | 0.835 | 0.834 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obata, K.; Yoshioka, H. A Simple Algorithm for Deriving an NDVI-Based Index Compatible between GEO and LEO Sensors: Capabilities and Limitations in Japan. Remote Sens. 2020, 12, 2417. https://doi.org/10.3390/rs12152417
Obata K, Yoshioka H. A Simple Algorithm for Deriving an NDVI-Based Index Compatible between GEO and LEO Sensors: Capabilities and Limitations in Japan. Remote Sensing. 2020; 12(15):2417. https://doi.org/10.3390/rs12152417
Chicago/Turabian StyleObata, Kenta, and Hiroki Yoshioka. 2020. "A Simple Algorithm for Deriving an NDVI-Based Index Compatible between GEO and LEO Sensors: Capabilities and Limitations in Japan" Remote Sensing 12, no. 15: 2417. https://doi.org/10.3390/rs12152417
APA StyleObata, K., & Yoshioka, H. (2020). A Simple Algorithm for Deriving an NDVI-Based Index Compatible between GEO and LEO Sensors: Capabilities and Limitations in Japan. Remote Sensing, 12(15), 2417. https://doi.org/10.3390/rs12152417