Model-Based Estimation of Forest Inventory Attributes Using Lidar: A Comparison of the Area-Based and Semi-Individual Tree Crown Approaches
Abstract
:1. Introduction
2. Materials
2.1. Study Area
2.2. Field Data
2.3. Lidar Data Acquisition and Processing
3. Methods
3.1. Constructing Population Units
3.1.1. Grid Cells
3.1.2. Segments
3.2. Unit-Level Model
3.3. Target Parameters
3.4. Predictions for Target Parameters
3.5. Model Selection
3.6. Mean Squared Error Estimators
4. Results
4.1. Selected Models
4.2. Estimation for the Study Region
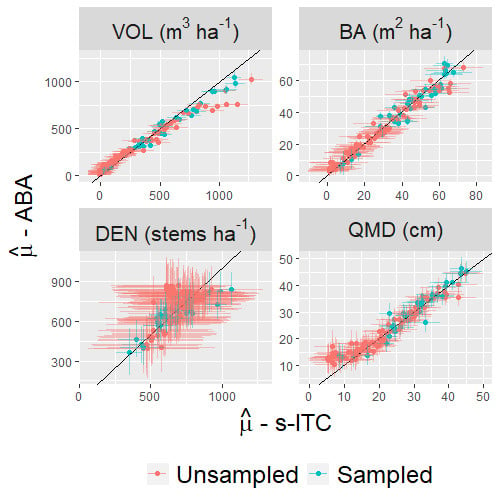
4.3. Estimation for Stands
5. Discussion
5.1. Contribution of Error Components
5.2. Peculiarities of a Segment Population
5.3. Implications for Forest Management Inventories
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Target Parameters and Their Components | |||
| Notation | Description | Notation | Description |
| for stand). | th population unit in the th area in hectares. | ||
| th area in hectares. | The sum of the areas of all population units in the entire study region in hectares. | ||
| Models and Their Components | |||
| Notation | Description | Notation | Description |
| A vector of observable quantities of the response variable for all population units. | A vector of residuals. | ||
| A design matrix of lidar covariates and an intercept for all population units. | A vector of regression coefficients. | ||
| A matrix that assigns population units to areas. | The variance-covariance matrix of . | ||
| A vector of realized random effects. | The variance-covariance matrix of . | ||
| The residual variance. | The random-effect variance. | ||
| . | , i.e., the number of field plots (ABA) or the number of segments (s-ITC) | ||
| Results Assessment Measures | |||
| Notation | Description | Notation | Description |
| The model-based root mean squared error for the predicted target parameter. | The relative change between s-ITC and ABA model-based root mean squared errors. | ||
| The approximate confidence interval for the predicted target parameter. | The estimated coefficient of variation of the predicted target parameter. | ||
Appendix B
| Predictor Name | Description |
|---|---|
| p_1, p_10, p_20, p_25, p_30, p_40, p_50, p_60, p_70, p_75, p_80, p_90, p_95, p_99 | The percentile of the z-dimension indicated by the trailing number. For example, p_95 describes the elevation at which 95% of the lidar points fall below. |
| max_z | The maximum z value. |
| min_z | The minimum z value. |
| mean_z | The mean z value. |
| stddev_z | The standard deviation of the z values. |
| var_z | The variance of the z values. |
| mean_z_sq | The square of the mean z value. |
| vol_cov | The product of the mean z value and the pct_r_1_above_2 metric. |
| pct_all_above_2 | The proportion of all returns above 2 m. |
| pct_all_above_mean | The proportion of all returns above the mean z value. |
| pct_r_1_above_2 | The proportion of first returns above 2 m. |
| pct_r_1_above_mean | The proportion of all returns above 2 m. |
| r_1, r_2, r_3, r_4 | The number of returns indicated by the trailing number. For example, r_1 indicates the number of first returns. |
| area | The area of the population unit (only included for s-ITC models) |
References
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T.; Yu, X.; Hyyppä, J.; Saari, H.; Pölönen, I.; Imai, N.; et al. Individual tree detection and classification with UAV-based photogrammetric point clouds and hyperspectral imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Wang, T.; Skidmore, A.K.; Heurich, M. Important LiDAR metrics for discriminating forest tree species in Central Europe. ISPRS J. Photogramm. Remote Sens. 2018, 137, 163–174. [Google Scholar] [CrossRef]
- Xu, Q.; Man, A.; Fredrickson, M.; Hou, Z.; Pitkänen, J.; Wing, B.; Ramirez, C.; Li, B.; Greenberg, J.A. Quantification of uncertainty in aboveground biomass estimates derived from small-footprint airborne LiDAR. Remote Sens. Environ. 2018, 216, 514–528. [Google Scholar] [CrossRef]
- Jeronimo, S.M.; Kane, V.R.; Churchill, D.J.; McGaughey, R.J.; Franklin, J.F. Applying LiDAR individual tree detection to management of structurally diverse forest landscapes. J. For. 2018, 116, 336–346. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Yang, Z.; Cohen, W.B.; Pflugmacher, D.; Lauver, C.L.; Vankat, J.L. Distinguishing between live and dead standing tree biomass on the North Rim of Grand Canyon National Park, USA using small-footprint lidar data. Remote Sens. Environ. 2009, 113, 2499–2510. [Google Scholar] [CrossRef]
- Wing, B.M.; Ritchie, M.W.; Boston, K.; Cohen, W.B.; Olsen, M.J. Individual snag detection using neighborhood attribute filtered airborne lidar data. Remote Sens. Environ. 2015, 163, 165–179. [Google Scholar] [CrossRef]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Loudermilk, E.L.; O’Brien, J.J.; Hiers, J.K.; Jack, S.B.; Gonzalez-Benecke, C.; Lee, H.; Falkowski, M.J.; et al. Imputation of individual Longleaf Pine (Pinus palustris Mill.) Tree attributes from field and LiDAR data. Can. J. Remote Sens. 2016, 42, 554–573. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ. 2010, 114, 911–924. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Astrup, R. Forest parameter prediction using an image-based point cloud: A comparison of semi-ITC with ABA. Forests 2015, 6, 4059–4071. [Google Scholar] [CrossRef]
- Breidenbach, J.; Astrup, R. The semi-individual tree crown approach. In Forestry Applications of Airborne Laser Scanning; Springer: Dordrecht, The Netherland, 2014; pp. 113–133. [Google Scholar]
- Hyyppa, J. Detecting and estimating attributes for single trees using laser scanner. Photogramm. J. Finl. 1999, 16, 27–42. [Google Scholar]
- Peuhkurinen, J.; Mehtätalo, L.; Maltamo, M. Comparing individual tree detection and the area-based statistical approach for the retrieval of forest stand characteristics using airborne laser scanning in Scots pine stands. Can. J. For. Res. 2011, 41, 583–598. [Google Scholar] [CrossRef]
- Breidenbach, J.; Astrup, R. Small area estimation of forest attributes in the Norwegian National Forest Inventory. Eur. J. Forest. Res. 2012, 131, 1255–1267. [Google Scholar] [CrossRef]
- Goerndt, M.E.; Monleon, V.J.; Temesgen, H. Small-area estimation of county-level forest attributes using ground data and remote sensed auxiliary information. For. Sci. 2013, 59, 536–548. [Google Scholar] [CrossRef]
- Magnussen, S.; Breidenbach, J. Model-dependent forest stand-level inference with and without estimates of stand-effects. Forestry (London) 2017, 90, 675–685. [Google Scholar] [CrossRef] [Green Version]
- Mauro, F.; Molina, I.; García-Abril, A.; Valbuena, R.; Ayuga-Téllez, E. Remote sensing estimates and measures of uncertainty for forest variables at different aggregation levels. Environmetrics 2016, 27, 225–238. [Google Scholar] [CrossRef]
- Hou, Z.; Mehtätalo, L.; McRoberts, R.E.; Stahl, G.; Tokola, T.; Rana, P.; Siipilehto, J.; Xu, Q. Remote sensing-assisted data assimilation and simultaneous inference for forest inventory. Remote Sens. Environ. 2019, 234, 111431. [Google Scholar] [CrossRef]
- Breidenbach, J.; Magnussen, S.; Rahlf, J.; Astrup, R. Unit-level and area-level small area estimation under heteroscedasticity using digital aerial photogrammetry data. Remote Sens. Environ. 2018, 212, 199–211. [Google Scholar] [CrossRef]
- Ubaidillah, A.; Notodiputro, K.A.; Kurnia, A.; Mangku, I.W. Multivariate Fay-Herriot models for small area estimation with application to household consumption per capita expenditure in Indonesia. J. Appl. Stat. 2019, 46, 2845–2861. [Google Scholar] [CrossRef]
- Leite, R.V.; do Amaral, C.H.; Pires, R.d.P.; Silva, C.A.; Soares, C.P.B.; Macedo, R.P.; da Silva, A.A.L.; Broadbent, E.N.; Mohan, M.; Leite, H.G. Estimating Stem Volume in Eucalyptus Plantations Using Airborne LiDAR: A Comparison of Area-and Individual Tree-Based Approaches. Remote Sens. 2020, 12, 1513. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd, ed.; Springer Science & Business Media: Berlin, Germany, 2009; ISBN 978-0-387-84858-7. [Google Scholar]
- Rao, J.N.K.; Molina, I. Small-Area Estimation, 2nd ed.; Wiley Series in Survey Methodology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Flewelling, J.W.; McFadden, G. LiDAR data and cooperative research at Panther Creek, Oregon. In Proceedings of the SilviLaser 2011, 11th International Conference on LiDAR Applications for Assessing Forest Ecosystems, Tasmania, Australia, 16–20 October 2011. [Google Scholar]
- Wang, Y. Volume Estimator Library Equations 2019. Available online: https://www.fs.fed.us/forestmanagement/products/measurement/volume/nvel/index.php (accessed on 4 August 2020).
- Zhang, K.; Chen, S.-C.; Whitman, D.; Shyu, M.-L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef] [Green Version]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. Nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 3.1-141. 2019. Available online: https://cran.r-project.org/web/packages/nlme/index.html (accessed on 4 August 2020).
- Lumley, T.; Lumley, M.T. Package ‘Leaps.’ Regression Subset Selection. Thomas Lumley Based on Fortran Code by Alan Miller, 2013. Available online: http://CRAN.R-project.org/package=leaps (accessed on 18 March 2018).
- Prasad, N.N.; Rao, J.N. The estimation of the mean squared error of small-area estimators. J. Am. Stat. Assoc. 1990, 85, 163–171. [Google Scholar] [CrossRef]
- Mauro, F.; Monleon, V.J.; Temesgen, H.; Ruiz, L.A. Analysis of spatial correlation in predictive models of forest variables that use LiDAR auxiliary information. Can. J. For. Res. 2017, 47, 788–799. [Google Scholar] [CrossRef] [Green Version]
- Packalen, P.; Strunk, J.; Packalen, T.; Maltamo, M.; Mehtätalo, L. Resolution dependence in an area-based approach to forest inventory with airborne laser scanning. Remote Sens. Environ. 2019, 224, 192–201. [Google Scholar] [CrossRef]
- Tang, S.; Dong, P.; Buckles, B.P. Three-dimensional surface reconstruction of tree canopy from lidar point clouds using a region-based level set method. Int. J. Remote Sens. 2013, 34, 1373–1385. [Google Scholar] [CrossRef]
- Strîmbu, V.F.; Strîmbu, B.M. A graph-based segmentation algorithm for tree crown extraction using airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 104, 30–43. [Google Scholar] [CrossRef] [Green Version]
- Yan, W.; Guan, H.; Cao, L.; Yu, Y.; Li, C.; Lu, J. A self-adaptive mean shift tree-segmentation method Using UAV LiDAR data. Remote Sens. 2020, 12, 515. [Google Scholar] [CrossRef] [Green Version]
- Kansanen, K.; Vauhkonen, J.; Lähivaara, T.; Mehtätalo, L. Stand density estimators based on individual tree detection and stochastic geometry. Can. J. For. Res. 2016, 46, 1359–1366. [Google Scholar] [CrossRef] [Green Version]
- Kangas, A.; Kangas, J.; Kurttila, M. Decision Support for Forest Management; Springer: Dordrecht, The Netherland, 2008. [Google Scholar]
- Wang, Y.; Hyyppä, J.; Liang, X.; Kaartinen, H.; Yu, X.; Lindberg, E.; Holmgren, J.; Qin, Y.; Mallet, C.; Ferraz, A.; et al. International Benchmarking of the Individual Tree Detection Methods for Modeling 3-D Canopy Structure for Silviculture and Forest Ecology Using Airborne Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5011–5027. [Google Scholar] [CrossRef] [Green Version]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in automatic individual tree crown detection and delineation—Evolution of LiDAR data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef] [Green Version]
- Mauro, F.; Monleon, V.J.; Temesgen, H.; Ford, K.R. Analysis of area level and unit level models for small area estimation in forest inventories assisted with LiDAR auxiliary information. PLoS ONE 2017, 12, e0189401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Magnussen, S.; Breidenbach, J. Retrieval of among-stand variances from one observation per stand. J. For. Sci. 2020, 66, 133–149. [Google Scholar] [CrossRef]
- Magnussen, S.; Breidenbach, J.; Mauro, F. The challenge of estimating a residual spatial autocorrelation from forest inventory data. Can. J. For. Res. 2017, 47, 1557–1566. [Google Scholar] [CrossRef] [Green Version]
- Breidenbach, J.; Næsset, E.; Gobakken, T. Improving k-nearest neighbor predictions in forest inventories by combining high and low density airborne laser scanning data. Remote Sens. Environ. 2012, 117, 358–365. [Google Scholar] [CrossRef]
- Kansanen, K.; Vauhkonen, J.; Lähivaara, T.; Seppänen, A.; Maltamo, M.; Mehtätalo, L. Estimating forest stand density and structure using Bayesian individual tree detection, stochastic geometry, and distribution matching. ISPRS J. Photogramm. Remote Sens. 2019, 152, 66–78. [Google Scholar] [CrossRef]








| Number of Field Plots | 0 | 1 | 2 | 3 | 4 | 5 | 7 |
| Number of Stands | 94 | 18 | 6 | 4 | 1 | 5 | 1 |
| Term | Definition |
|---|---|
| Grid cell | A square area 0.08 hectares in size. The population unit for the ABA. |
| Population | The set of all geographical units, either grid cells for the ABA or segments for the s-ITC approach, used in the analysis. |
| Segment | An irregular polygon of varying size produced by a segmentation procedure. The population unit for the s-ITC approach. |
| Stand | An area of homogeneous forest structure used as a small area of interest. If a stand contains at least one field plot it is considered “sampled”, if it does not it is considered “unsampled”. Stands are indexed by . |
| Stand-specific sample size | The sample size for a particular stand, denoted by . For the area-based approach, this refers to the number of field plots in the stand. For the s-ITC this refers to the number of sample segments in the stand, i.e., those segments contained in the field plots (Figure 2). |
| Study region | The set of 129 stands included in the analysis. |
| Attribute | Source | Mean | Std. Dev. | Minimum | Maximum |
|---|---|---|---|---|---|
| VOL ) | Field Plots | 601.3 | 389.4 | 3.3 | 1733.3 |
| Segments | 542.6 | 340.8 | 0.0 | 1975.3 | |
| BA ) | Field Plots | 48.7 | 23.7 | 1.8 | 102.0 |
| Segments | 46.0 | 22.3 | 0.0 | 148.5 | |
| DEN ) | Field Plots | 31.9 | 12.8 | 160.6 | 1519.9 |
| Segments | 30.1 | 12.1 | 0.0 | 4019.9 | |
| QMD ) | Field Plots | 659.3 | 277.2 | 5.3 | 69.1 |
| Segments | 687.8 | 302.2 | 0.0 | 82.8 |
| Attribute | Model | Predictor | Coefficient | Std. Error | |||
|---|---|---|---|---|---|---|---|
| VOL () | ABA | Intercept mean_z mean_z_sq | −8.09 10.50 0.83 | 12.90 4.02 0.15 | 0.5 | 0.00 1 | 7.37 |
| s-ITC | Intercept mean_z_sq | −20.27 1.25 | 16.66 0.04 | 0.5 | 61.65 | 8.23 | |
| BA () | ABA | Intercept P_60 | 0.74 1.98 | 1.50 0.08 | 0.5 | 0.00 1 | 2.33 |
| s-ITC | Intercept vol_cov | −2.24 2.50 | 1.69 0.08 | 0.5 | 5.7 | 3.53 | |
| DEN () | ABA | Intercept P_80 vol_cov | 935.42 −33.84 34.32 | 77.92 7.06 9.21 | 0.0 | 73.17 | 228.14 |
| s-ITC | Intercept canopy_relief_ratio P_95 | 210.17 1301.40 −10.26 | 96.32 152.93 3.41 | 0.5 | 175.32 | 614.55 | |
| QMD () | ABA | Intercept canopy_relief_ratio P_60 | 16.79 −28.59 1.26 | 3.57 7.88 0.08 | 0.0 | 1.43 | 5.83 |
| s-ITC | Intercept P_80 Pct_r_1_above_2m | 1.68 0.99 3.09 | 0.98 0.05 0.87 | 0.5 | 2.72 | 1.54 |
| Attribute | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| ABA | s-ITC | ABA | s-ITC | ABA | s-ITC | ABA | s-ITC | ||
| VOL ) | 395.73 | 417.22 | 159.94 | 166.05 | 3.12% | 3.09% | 12.65 | 12.89 | 1.90% |
| BA ) | 35.32 | 36.03 | 1.06 | 1.50 | 2.91% | 3.40% | 1.22 | 1.03 | −15.57% |
| ) | 696.27 | 701.13 | 1225.02 | 1690.60 | 5.03% | 5.86% | 35.00 | 41.12 | 17.49% |
| QMD ) | 25.37 | 24.97 | 0.77 | 0.36 | 3.47% | 2.39% | 0.87 | 0.60 | −31.03% |
| Attribute | Sampled | |||||
|---|---|---|---|---|---|---|
| ABA | s-ITC | ABA | s-ITC | |||
| VOL () | S | 2.3% | 4.9% | 9.7 | 29.9 | 208.2% |
| U | 4.5% | 18.7% | 9.4 | 48.4 | 414.9% | |
| BA () | S | 2.3% | 6.1% | 1.1 | 2.5 | 127.3% |
| U | 4.6% | 21.0% | 1.2 | 5.4 | 350.0% | |
| DEN ) | S | 4.8% | 3.7% | 32.3 | 22.8 | −29.4% |
| U | 12.1% | 26.4% | 89.4 | 183.0 | 104.7% | |
| QMD () | S | 3.5% | 5.8% | 1.2 | 1.7 | 41.7% |
| U | 10.0% | 12.7% | 1.9 | 2.6 | 36.8% | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frank, B.; Mauro, F.; Temesgen, H. Model-Based Estimation of Forest Inventory Attributes Using Lidar: A Comparison of the Area-Based and Semi-Individual Tree Crown Approaches. Remote Sens. 2020, 12, 2525. https://doi.org/10.3390/rs12162525
Frank B, Mauro F, Temesgen H. Model-Based Estimation of Forest Inventory Attributes Using Lidar: A Comparison of the Area-Based and Semi-Individual Tree Crown Approaches. Remote Sensing. 2020; 12(16):2525. https://doi.org/10.3390/rs12162525
Chicago/Turabian StyleFrank, Bryce, Francisco Mauro, and Hailemariam Temesgen. 2020. "Model-Based Estimation of Forest Inventory Attributes Using Lidar: A Comparison of the Area-Based and Semi-Individual Tree Crown Approaches" Remote Sensing 12, no. 16: 2525. https://doi.org/10.3390/rs12162525
APA StyleFrank, B., Mauro, F., & Temesgen, H. (2020). Model-Based Estimation of Forest Inventory Attributes Using Lidar: A Comparison of the Area-Based and Semi-Individual Tree Crown Approaches. Remote Sensing, 12(16), 2525. https://doi.org/10.3390/rs12162525