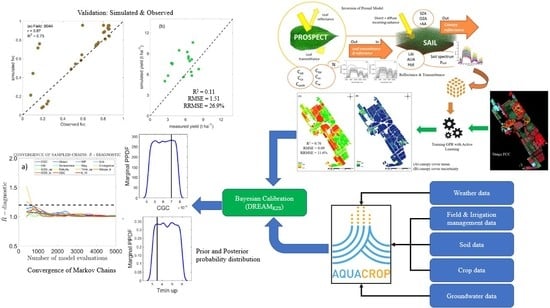
Bayesian Calibration of the Aquacrop-OS Model for Durum Wheat by Assimilation of Canopy Cover Retrieved from VENµS Satellite Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. VENµS Satellite Data
2.2. Retrieval of fvc from VENµS Satellite Data
2.3. Smoothing and Fitting fvc Time Series Data Retrieved From Venµs Satellite Data
2.4. Study Site and Ground Validation Campaigns
2.5. Weather Data
2.6. Aquacrop-OS Model and Sensitive Parameters
2.7. Markov Chain Monte Carlo-Based DREAM(KZS) Algorithm
2.8. Statistical Analysis and Validation
3. Results
3.1. fvc Retrieval
3.2. Parameters Identification
3.3. Calibration and Validation
3.3.1. fvc
3.3.2. Biomass and Yield
4. Discussions
4.1. fvc Retrieval
4.2. Parameters Identification
4.3. Calibration and Validation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lobell, D.B. The use of satellite data for crop yield gap analysis. Field Crop. Res. 2013, 143, 56–64. [Google Scholar] [CrossRef] [Green Version]
- Azzari, G.; Jain, M.; Lobell, D.B. Towards fine resolution global maps of crop yields: Testing multiple methods and satellites in three countries. Remote Sens. Environ. 2017, 202, 129–141. [Google Scholar] [CrossRef]
- Zaks, D.P.; Kucharik, C.J. Data and monitoring needs for a more ecological agriculture. Environ. Res. Lett. 2011, 6, 014017. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Sinclair, T.R.; Hollinger, S.; Akhmedov, B.; Stern, A.; Prueger, J. Application of MODIS derived parameters for regional crop yield assessment. Remote Sens. Environ. 2005, 97, 192–202. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P.; Ortiz-Monasterio, J.I.; Benning, T.L. Remote sensing of regional crop production in the Yaqui Valley, Mexico: Estimates and uncertainties. Agric. Ecosyst. Environ. 2003, 94, 205–220. [Google Scholar] [CrossRef] [Green Version]
- Thorp, K.; Wang, G.; West, A.; Moran, M.; Bronson, K.; White, J.; Mon, J. Estimating crop biophysical properties from remote sensing data by inverting linked radiative transfer and ecophysiological models. Remote Sens. Environ. 2012, 124, 224–233. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Li, Z.; Yang, G.; Yang, H.; Feng, H.; Xu, X.; Wang, J.; Li, X.; Luo, J. Winter wheat yield estimation based on multi-source medium resolution optical and radar imaging data and the AquaCrop model using the particle swarm optimization algorithm. ISPRS J. Photogramm. Remote Sens. 2017, 126, 24–37. [Google Scholar] [CrossRef]
- Jin, Z.; Azzari, G.; Lobell, D.B. Improving the accuracy of satellite-based high-resolution yield estimation: A test of multiple scalable approaches. Agric. For. Meteorol. 2017, 247, 207–220. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Gervois, S.; de Noblet-Ducoudré, N.; Viovy, N.; Ciais, P.; Brisson, N.; Seguin, B.; Perrier, A. Including croplands in a global biosphere model: Methodology and evaluation at specific sites. Earth Interact. 2004, 8, 1–25. [Google Scholar] [CrossRef]
- De Willigen, P. Nitrogen turnover in the soil-crop system; comparison of fourteen simulation models. Fertil. Res. 1991, 27, 141–149. [Google Scholar] [CrossRef]
- Hopmans, J.W.; Bristow, K.L. Current capabilities and future needs of root water and nutrient uptake modeling. Adv. Agron. 2002, 77, 103–183. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Campolongo, F. Sensitivity analysis as an ingredient of modeling. Stat. Sci. 2000, 15, 377–395. [Google Scholar]
- Wallach, D.; Goffinet, B.; Bergez, J.-E.; Debaeke, P.; Leenhardt, D.; Aubertot, J.-N. Parameter estimation for crop models: A new approach and application to a corn model. Agron. J. 2001, 93, 757–766. [Google Scholar] [CrossRef]
- Makowski, D.; Hillier, J.; Wallach, D.; Andrieu, B.; Jeuffroy, M. Parameter estimation for crop models. In Working with Dynamic Models. Evaluation, Analysis, Parameterization and Applications; Elsevier: Amsterdam, The Netherlands, 2006; pp. 101–149. [Google Scholar]
- Silvestro, P.C.; Pignatti, S.; Yang, H.; Yang, G.; Pascucci, S.; Castaldi, F.; Casa, R. Sensitivity analysis of the Aquacrop and SAFYE crop models for the assessment of water limited winter wheat yield in regional scale applications. PLoS ONE 2017, 12, e0187485. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- He, B.; Li, X.; Quan, X.; Qiu, S. Estimating the aboveground dry biomass of grass by assimilation of retrieved LAI into a crop growth model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 550–561. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Xu, X.; Yang, G.; Wang, J. Estimation of winter wheat biomass and yield by combining the aquacrop model and field hyperspectral data. Remote Sens. 2016, 8, 972. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Gupta, H.V.; Bastidas, L.A.; Bouten, W.; Sorooshian, S. Effective and efficient algorithm for multiobjective optimization of hydrologic models. Water Resour. Res. 2003, 39, 5.1–5.19. [Google Scholar] [CrossRef] [Green Version]
- Jeon, J.-H.; Park, C.-G.; Engel, B.A. Comparison of performance between genetic algorithm and SCE-UA for calibration of SCS-CN surface runoff simulation. Water 2014, 6, 3433–3456. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Model. Softw. 2016, 75, 273–316. [Google Scholar] [CrossRef] [Green Version]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Beichl, I.; Sullivan, F. The metropolis algorithm. Comput. Sci. Eng. 2000, 2, 65–69. [Google Scholar] [CrossRef] [Green Version]
- Haario, H.; Saksman, E.; Tamminen, J. Adaptive proposal distribution for random walk Metropolis algorithm. Comput. Stat. 1999, 14, 375–396. [Google Scholar] [CrossRef]
- Haario, H.; Saksman, E.; Tamminen, J. An adaptive Metropolis algorithm. Bernoulli 2001, 7, 223–242. [Google Scholar] [CrossRef] [Green Version]
- Haario, H.; Laine, M.; Mira, A.; Saksman, E. DRAM: Efficient adaptive MCMC. Stat. Comput. 2006, 16, 339–354. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Bouten, W.; Sorooshian, S. A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2003, 39, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Ter Braak, C.J. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F.; Diks, C.G.H.; Robinson, B.A.; Hyman, J.M.; Higdon, D. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar] [CrossRef]
- Laloy, E.; Vrugt, J.A. High-dimensional posterior exploration of hydrologic models using multiple-try DREAM (ZS) and high-performance computing. Water Resour. Res. 2012, 48, W01526. [Google Scholar] [CrossRef] [Green Version]
- Laloy, E.; Rogiers, B.; Vrugt, J.A.; Mallants, D.; Jacques, D. Efficient posterior exploration of a high-dimensional groundwater model from two-stage Markov chain Monte Carlo simulation and polynomial chaos expansion. Water Resour. Res. 2013, 49, 2664–2682. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Ter Braak, C.J. DREAM (D): An adaptive Markov Chain Monte Carlo simulation algorithm to solve discrete, noncontinuous, and combinatorial posterior parameter estimation problems. Hydrol. Earth Syst. Sci. 2011, 15, 3701–3713. [Google Scholar] [CrossRef] [Green Version]
- Sadegh, M.; Vrugt, J.A. Approximate bayesian computation using Markov chain Monte Carlo simulation: DREAM (ABC). Water Resour. Res. 2014, 50, 6767–6787. [Google Scholar] [CrossRef] [Green Version]
- Evensen, G. Data Assimilation: The Ensemble Kalman Filter; Springer Science and Business Media: Berlin, Germany, 2009; ISBN 3-642-03711-9. [Google Scholar]
- Zhang, J.; Vrugt, J.A.; Shi, X.; Lin, G.; Zeng, L.; Wu, L. Speed-up of posterior inference of highly-parameterized environmental models from a Kalman proposal distribution: DREAM (KZS). arXiv 2017, arXiv:1707.05431. [Google Scholar]
- Castaldi, F.; Casa, R.; Pelosi, F.; Yang, H. Influence of acquisition time and resolution on wheat yield estimation at the field scale from canopy biophysical variables retrieved from SPOT satellite data. Int. J. Remote Sens. 2015, 36, 2438–2459. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop—The FAO crop model to simulate yield response to water: I. Concepts and underlying principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef] [Green Version]
- Silvestro, P.C.; Casa, R.; Pignatti, S. Development of an Assimilation Scheme for the Estimation of Drought-Induced Yield Losses Based on Multi-Source Remote Sensing and the AcquaCrop Model. In Proceedings of the Dragon 3 Mid-Term Results Symposium, Chengdu, China, 26–29 May 2014. [Google Scholar]
- Foster, T. AquaCrop-OS v5.0a Reference Manual; FAO: Rome, Italy, 2016. [Google Scholar]
- Foster, T. AquaCrop-OS v6.0a Reference Manual; FAO: Rome, Italy, 2019. [Google Scholar]
- Ferrier, P.; Crebassol, P.; Dedieu, G.; Hagolle, O.; Meygret, A.; Tinto, F.; Yaniv, Y.; Herscovitz, J. VENµS (Vegetation and environment monitoring on a new micro satellite). In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3736–3739. [Google Scholar]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Upreti, D.; Huang, W.; Kong, W.; Pascucci, S.; Pignatti, S.; Zhou, X.; Ye, H.; Casa, R. A comparison of hybrid machine learning algorithms for the retrieval of wheat biophysical variables from sentinel-2. Remote Sens. 2019, 11, 481. [Google Scholar] [CrossRef] [Green Version]
- Weiss, M.; Baret, F. S2ToolBox Level 2 Products: Lai, Fapar, Fcover; Institut National de la Recherche Agronomique (INRA): Paris, France, 2016. [Google Scholar]
- Velleman, P.F.; Hoaglin, D.C. Applications, Basics, and Computing of Exploratory Data Analysis; Duxbury Press: Boston, MA, USA, 1981; ISBN 0-87150-409-X. [Google Scholar]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.; Özdoğan, M. Field-level crop yield mapping with Landsat using a hierarchical data assimilation approach. Remote Sens. Environ. 2019, 228, 144–163. [Google Scholar] [CrossRef]
- LI-COR Biosciences. LAI 2000 Plant Canopy Analyzer. Operating Manual; LI-COR Biosciences: Lincoln, NE, USA, 1992. [Google Scholar]
- Nielsen, D.C.; Miceli-Garcia, J.J.; Lyon, D.J. Canopy cover and leaf area index relationships for wheat, triticale, and corn. Agron. J. 2012, 104, 1569–1573. [Google Scholar] [CrossRef] [Green Version]
- Whelan, B.M.; McBratney, A.B.; Minasny, B. Vesper–Spatial Prediction Software for Precision Agriculture. In ECPA 2001, Proceedings of the 3rd European Conference on Precision Agriculture, Montpellier, France, 2001; Grenier, G., Blackmore, S., Eds.; Agro-Montpellier: Montpellier, France, 2001; pp. 139–144. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Raes, D. The ETo Calculator, Evapotranspiration from a Reference Surface. Reference Manual Version 3.1, January; Food and Agricultural Organization of the United Nations: Rome, Italy, 2009. [Google Scholar]
- Todorovic, M.; Albrizio, R.; Zivotic, L.; Saab, M.-T.A.; Stöckle, C.; Steduto, P. Assessment of AquaCrop, CropSyst, and WOFOST models in the simulation of sunflower growth under different water regimes. Agron. J. 2009, 101, 509–521. [Google Scholar] [CrossRef]
- Saab, M.T.A.; Todorovic, M.; Albrizio, R. Comparing AquaCrop and CropSyst models in simulating barley growth and yield under different water and nitrogen regimes. Does calibration year influence the performance of crop growth models? Agric. Water Manag. 2015, 147, 21–33. [Google Scholar] [CrossRef]
- Xiangxiang, W.; Quanjiu, W.; Jun, F.; Qiuping, F. Evaluation of the AquaCrop model for simulating the impact of water deficits and different irrigation regimes on the biomass and yield of winter wheat grown on China’s Loess Plateau. Agric. Water Manag. 2013, 129, 95–104. [Google Scholar] [CrossRef]
- Andarzian, B.; Bannayan, M.; Steduto, P.; Mazraeh, H.; Barati, M.; Barati, M.; Rahnama, A. Validation and testing of the AquaCrop model under full and deficit irrigated wheat production in Iran. Agric. Water Manag. 2011, 100, 1–8. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Estimation of maize yield by assimilating biomass and canopy cover derived from hyperspectral data into the AquaCrop model. Agric. Water Manag. 2020, 227, 105846. [Google Scholar] [CrossRef]
- Foster, T.; Brozovic, N.; Butler, A.P.; Neale, C.M.; Raes, D.; Steduto, P.; Fereres, E.; Hsiao, T.C. AquaCrop-OS: A tool for resilient management of land and water resources in agriculture. EGUGA 2017, 19, 2842. [Google Scholar]
- Upreti, D.; Pignatti, S.; Pascucci, S.; Tolomio, M.; Li, Z.; Huang, W.; Casa, R. A comparison of moment-independent and variance-based global sensitivity analysis approaches for wheat yield estimation with the Aquacrop-OS model. Agronomy 2020, 10, 607. [Google Scholar] [CrossRef]
- Van Oijen, M.; Rougier, J.; Smith, R. Bayesian calibration of process-based forest models: Bridging the gap between models and data. Tree Physiol. 2005, 25, 915–927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wallach, D.; Makowski, D.; Jones, J.W.; Brun, F. Working with Dynamic Crop Models: Methods, Tools and Examples for Agriculture and Environment; Academic Press: Cambridge, MA, USA, 2018; ISBN 0-12-811757-5. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods–A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Trombetta, A.; Iacobellis, V.; Tarantino, E.; Gentile, F. Calibration of the AquaCrop model for winter wheat using MODIS LAI images. Agric. Water Manag. 2016, 164, 304–316. [Google Scholar] [CrossRef]
- Ma, Q.; Su, Y.; Guo, Q. Comparison of canopy cover estimations from airborne LiDAR, aerial imagery, and satellite imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4225–4236. [Google Scholar] [CrossRef]
- Silvestro, P.; Pignatti, S.; Pascucci, S.; Yang, H.; Li, Z.; Yang, G.; Huang, W.; Casa, R. Estimating wheat yield in China at the field and district scale from the assimilation of satellite data into the Aquacrop and simple algorithm for yield (SAFY) models. Remote Sens. 2017, 9, 509. [Google Scholar] [CrossRef] [Green Version]
- Revill, A.; Florence, A.; MacArthur, A.; Hoad, S.P.; Rees, R.M.; Williams, M. The value of Sentinel-2 spectral bands for the assessment of winter wheat growth and development. Remote Sens. 2019, 11, 2050. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Su, J.; Liu, C.; Chen, W.-H. Bayesian calibration of AquaCrop model for winter wheat by assimilating UAV multi-spectral images. Comput. Electron. Agric. 2019, 167, 105052. [Google Scholar] [CrossRef]
- Camargo Rodriguez, A.V.; Ober, E.S. AquaCropR: Crop Growth Model for R. Agronomy 2019, 9, 378. [Google Scholar] [CrossRef] [Green Version]











| Bands | Central Wavelength (nm) | Bandwidth (nm) | Main Applications |
|---|---|---|---|
| B1 | 420 | 25 | Atmospheric Correction Water |
| B2 | 443 | 40 | Aerosols, Clouds |
| B3 | 490 | 20 | Atmospheric Correction, Water |
| B4 | 555 | 20 | Land |
| B5 | 638 | 24 | Vegetation Indices |
| B6 | 638 | 24 | DEM, Image Quality |
| B7 | 672 | 16 | Red Edge |
| B8 | 702 | 24 | Red Edge |
| B9 | 742 | 16 | Red Edge |
| B10 | 782 | 16 | Red Edge |
| B11 | 865 | 20 | Vegetation Indices |
| B12 | 910 | 20 | Water Vapor |
| AOS Model Calibration Data | AOS Model Validation Data |
|---|---|
| fvc time series of 2017–2018 retrieved from VENµS data(20 pixels that represents yield variability) |
|
| Date—Ground Measurements | Date—VENµS Acquisition | Difference (Days) |
|---|---|---|
| 31 January 2018 | 28 January 2018 | 3 |
| 16 February 2018 | 13 February 2018 | 3 |
| 6 April 2018 | 8 April 2018 | 2 |
| 20 April 2018 | 20 April 2018 | 0 |
| Parameter | Unit | AOS Standard | Prior Range | Estimated Parameter |
|---|---|---|---|---|
| CGC | fraction GDD | 0.0050 | (0.0042, 0.0078) | 0.0060 |
| HIstart | GDD | 1250 | (1090, 1395) | 1243 |
| WP | gm−2 | 15 | (11, 22) | 16.50 |
| Kcb | - | 1.10 | (0.77, 1.43) | 1.10 |
| HI0 | % | 0.48 | (0.32, 0.59) | 0.46 |
| Senescence | GDD | 1700 | (1090, 2250) | 1670 |
| Wpy | gm−2 | 100.00 | (75, 125) | 100.00 |
| Emergence | GDD | 150 | (90, 230) | 160 |
| GDD_up | GDD | 14 | (9, 18) | 13.50 |
| Maturity | GDD | 2400 | (1590, 3150) | 2370 |
| Tmin_up | °C | 5 | (3, 6) | 4.50 |
| fshape_b | - | 13.81 | (9.6694, 17.9575) | 13.81 |
| GDD_lo | GDD | 0 | (0, 5) | 2.5 |
| CDC | fraction GDD | 0.0040 | (0.0028, 0.0052) | 0.0040 |
| b_HI | - | 7 | (3, 6) | 4.50 |
| Field Code | RMSE | RE | α | β | r | KGE |
|---|---|---|---|---|---|---|
| B031 | 0.16 | 0.25 | 1.11 | 1.03 | 0.87 | 0.18 |
| B032 | 0.19 | 0.60 | 0.96 | 1.07 | 0.83 | 0.15 |
| B044 | 0.20 | 0.44 | 1.11 | 1.13 | 0.87 | 0.22 |
| B062 | 0.41 | 2.79 | 0.84 | 1.9 | 0.61 | 0.93 |
| B069 | 0.44 | 2.29 | 0.88 | 1.95 | 0.52 | 0.97 |
| B085 | 0.23 | 0.65 | 0.96 | 1.30 | 0.86 | 0.33 |
| B109 | 0.15 | 0.19 | 1.45 | 0.91 | 0.93 | 0.47 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Upreti, D.; Pignatti, S.; Pascucci, S.; Tolomio, M.; Huang, W.; Casa, R. Bayesian Calibration of the Aquacrop-OS Model for Durum Wheat by Assimilation of Canopy Cover Retrieved from VENµS Satellite Data. Remote Sens. 2020, 12, 2666. https://doi.org/10.3390/rs12162666
Upreti D, Pignatti S, Pascucci S, Tolomio M, Huang W, Casa R. Bayesian Calibration of the Aquacrop-OS Model for Durum Wheat by Assimilation of Canopy Cover Retrieved from VENµS Satellite Data. Remote Sensing. 2020; 12(16):2666. https://doi.org/10.3390/rs12162666
Chicago/Turabian StyleUpreti, Deepak, Stefano Pignatti, Simone Pascucci, Massimo Tolomio, Wenjiang Huang, and Raffaele Casa. 2020. "Bayesian Calibration of the Aquacrop-OS Model for Durum Wheat by Assimilation of Canopy Cover Retrieved from VENµS Satellite Data" Remote Sensing 12, no. 16: 2666. https://doi.org/10.3390/rs12162666
APA StyleUpreti, D., Pignatti, S., Pascucci, S., Tolomio, M., Huang, W., & Casa, R. (2020). Bayesian Calibration of the Aquacrop-OS Model for Durum Wheat by Assimilation of Canopy Cover Retrieved from VENµS Satellite Data. Remote Sensing, 12(16), 2666. https://doi.org/10.3390/rs12162666