Next Article in Journal
Long-Term Discharge Estimation for the Lower Mississippi River Using Satellite Altimetry and Remote Sensing Images
Next Article in Special Issue
Evaluating the Effects of Digital Elevation Models in Landslide Susceptibility Mapping in Rangamati District, Bangladesh
Previous Article in Journal
An Effective Lunar Crater Recognition Algorithm Based on Convolutional Neural Network
Previous Article in Special Issue
Mapping, Monitoring, and Prediction of Floods Due to Ice Jam and Snowmelt with Operational Weather Satellites
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 17
10.3390/rs12172695
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Flash Flood Susceptibility Modeling and Magnitude Index Using Machine Learning and Geohydrological Models: A Modified Hybrid Approach

by
Samy Elmahdy
1,*,
Tarig Ali
1 and
Mohamed Mohamed
2,3
1
GIS and Mapping Laboratory, Civil Engineering Department, College of Engineering, American University of Sharjah, P.O. Box 26666, Sharjah, UAE
2
Civil and Environmental Engineering Department, United Arab Emirates University, Al-Ain P.O. Box 15551, UAE
3
National Water Center, United Arab Emirates University, Al Ain, P.O. Box 15551, Abu Dhabi, UAE
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(17), 2695; https://doi.org/10.3390/rs12172695
Submission received: 8 July 2020 / Revised: 10 August 2020 / Accepted: 14 August 2020 / Published: 20 August 2020
(This article belongs to the Special Issue Remote Sensing of Natural Hazards)
Browse Figures
Versions Notes

Abstract

:
In an arid region, flash floods (FF), as a response to climate changes, are the most hazardous causing massive destruction and losses to farms, human lives and infrastructure. A first step towards securing lives and infrastructure is the susceptibility mapping and predicting of occurrence sites of FF. Several studies have been applied using an ensemble machine learning model (EMLM) but measuring FF magnitude using a hybrid approach that integrates machine learning (MCL) and geohydrological models have not been widely applied. This study aims to modify a hybrid approach by testing three machine learning models. These are boosted regression tree (BRT), classification and regression trees (CART), and naive Bayes tree (NBT) for FF susceptibility mapping at the northern part of the United Arab Emirates (NUAE). This is followed by applying a group of accuracy metrics (precision, recall and F1 score) and the receiving operating characteristics (ROC) curve. The result demonstrated that the BRT has the highest performance for FF susceptibility mapping followed by the CART and NBT. After that, the produced FF map using the BRT was then modified by dividing it into seven basins, and a set of new FF conditioning parameters namely alluvial plain width, basin gradient and mean slope for each basin was calculated for measuring FF magnitude. The results showed that the mountainous and narrower basins (e.g., RAK, Masafi, Fujairah, and Rol Dadnah) have the highest probability occurrence of FF and FF magnitude, while the wider alluvial plains (e.g., Al Dhaid) have the lowest probability occurrence of FF and FF magnitude. The proposed approach is an effective approach to improve the susceptibility mapping of FF, landslides, land subsidence, and groundwater potentiality obtained using ensemble machine learning, which is used widely in the literature.

Graphical Abstract

1. Introduction

Flash floods are a temporary overflow of rivers or valley plains as a natural response to unusually heavy rains. They can cause damage to infrastructure and human life [1,2]. FF usually occur frequently at narrow mountainous valleys (wadis), alluvial fans at the foot of mountainous and narrow coastal areas as a response to climate change and intensive rainfall over an impermeable and an impervious surface [3,4]. Globally, about one-third of the Earth’s surface (where more than 70% of the world population reside), frequently experiences to flash flooding [5].
The UAE, including the study area, has not escaped this natural hazard since it experiences several flash flooding on a regional scale. The northern part of the UAE recorded huge amounts of rain between 9 January and 12 January 2020. The heaviest rainfall was 24 years ago in Khor Fakkan with 144 mm (5.66 inches) of accumulated rainfall (https://www.ncm.ae). In Ras Al Khaimah (RAK), one woman was crushed to death after a wall collapsed during a violent storm.
In Ghalilah and Al Fahlain villages of the RAK, flash floods destroyed roads, farms and flooded the village graveyard (Figure 1). Away from the mountainous areas, the cities of Sharjah and Dubai have experienced monstrous floods consuming roads and vital areas such as Terminal 1 of Dubai International Airport, shopping malls and Jabal Ali (https://www.ncm.ae). Flash flooding events solely depend on several terrain and geohydrological parameters such as alluvial plain width, mountainous valley width, altitude, topographic slopes, topographic curvature, steam density, topographic relief, the angle of repose and, of course, the intensity of rainfall. The angle of repose or talus slope ranges between 25 and 40 and depends upon the nature and type of the rocks and is directionally proportional to the flash flood magnitude [6].
These consequences can be controlled or, at least, reduced by constructing a regional and precise susceptibility mapping and analysis [7] and calculating the angle of repose or talus for each hydrological basin. Thus, building an accurate geohazard model and measuring flash flood magnitude over a regional scale is one of the researchers and decision-makers important task [8]. Susceptibility can be defined as a prediction of where the future hazardous event is likely to occur [9,10]. The wide availability of free of charge remote sensing data and machine learning algorithms allowed researchers to susceptibility map and predict flash floods over a regional scale efficiently and economically [11,12,13,14].
Several hydrological models have been developed using hydrological parameters such as rainfall and runoff [15,16,17,18,19]. However, these techniques have been built based on a single dimension and changeable parameters due to climate change and soil erosion. Additionally, these models lack sensitive analysis and field observation. Other studies have been applied for FF susceptible mapping using the data-driven and K-nearest neighbors (K-NN) [20,21,22,23], analytic hierarchy process (AHP) [24], frequency ratio (FR) [25], firefly algorithm (FA) [26,27], feature selection method (FSM) [26], support vector machine (SVM) [27] artificial neural network (ANN) [28], and weight of evidence (WoE) [29], and decision tree (DT) [30,31].
A novel approach has been employed for flood susceptibility mapping [29,30,31,32,33]. Recently, a comparative assessment of decision tree algorithms for susceptibility modeling has been performed [34,35,36]. Most of these studies have been focused on susceptibility mapping of FF using ensemble machine learning or a comparative assessment of machine learning algorithms. However, these studies have not focused on FF conditioning parameters such as alluvial plain width, valley width and basin slope. Additionally, the magnitudes of FF has not been taken into considerations. This study aims to modify a hybrid integration approach for flash flood susceptibility mapping in an arid region. Here, we first performed a comparison between BRT, CART, and NBT models for FF susceptibility mapping for the first time. The best FF susceptibility map was chosen and then modified by dividing it into seven basins. Each basin has its own FF magnitude. The FF magnitude was calculated using four new FFCPs namely alluvial plain width, valley width, basin gradient and mean slope. The proposed approach represents an advancement step to modify predicted maps of FF, landslides, land subsidence and groundwater potential produced using machine learning models. The modified approach can be of great help to risk management specialists and geohazard prevention scientists.

2. Study Area

The study area stretches from longitude 54°58’21”E to 56°29’42”E and latitude 24°33’45”N to 26°5’24”N and has an area of about 11,871 km2. It includes the Emirates of Dubai, Sharjah, Ajman, Umm Al Quwain, Ras al Khaimah and Fujairah (Figure 2). Most of the built-up area is concentrated on coastal strips and waterfronts such as creeks and artificial lakes, while the agricultural area is limited to the alluvial plains, wherever rainfall and paleochannels (wadis) are found.
The area is characterized by narrow alluvial coastal plains in the north-western and the eastern parts of the study area with a width ranging from 2 to 5 km, reaching its maximum width at Falahyeen and Al Dhaid villages (No. 9 and 19 in Figure 2). Lithologically, the upper streams (mountainous areas) are dominated by the igneous and metamorphic rocks in the east and carbonate rocks in the north and alluvial deposits at the foot of the mountainous areas [13]. The area has weather varying from hot and humid during the summer and being warm during the winter (Figure 3a). The annual rainfall varies from 30 mm in the south-eastern desert near the city of Dubai to 180 mm in the mountainous areas in the north and east [37,38]. The maximum number of rainfall days over the study is four to six days per month during the period from December to March (Figure 3b). The maximum daily precipitation value is 1.2 mm during March (Figure 3c) (Giri and Singh 2015). The estimated annual rainfall over the mountainous and coastal areas was about 97% of total rainfall over the NUAE [38].
Hydrologically, the area is comprised of three aquifers: a carbonate, ophiolite, coastal, and an alluvial. The aquifers are drained by several surface wadi courses. Their trends are common in the NW-SE, NNW-SSE, NE-SW and NNE-SSW directions [39,40]. These features play an important role in flash floods by accumulating rainwater from upstream and crash houses and farms in the downstream [39].

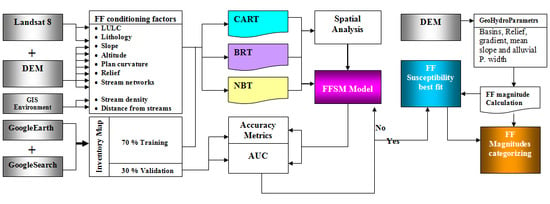
3. Datasets and Methodology

The proposed approach can briefly be described as the following steps: (i) constructing a flash flood inventory map (dependent variable), (ii) constructing flash floods conditioning parameters (independent variables), (iii) spatially analyzing the relationship between each conditioning parameter and flash flood events, (iv) optimal parameterization and flash flooding susceptibility mapping, (v) evaluating the performance and assessing the accuracy of machine learning models, and (vi) dividing the area into seven basins and calculating flash floods magnitude for each basin. A flowchart of the methodology adopted in the current study is shown in Figure 4.

3.1. Construction of Flash Floods Inventory Map (FFIM)

FFIM is an excellent indicator for FF susceptibility mapping. Here we used several sources including Google searches, the Google Earth application and local reports of newspapers and weather. These reports were collected and downloaded via the webpage of the National Centre of Metrology webpage (https://www.ncm.ae/Radar_UAE_Merge). Since 1990, 61 flash flood events were reported across the study area, and the most severe event happened between 9 and 12 January 2020 with 144 mm (5.66 inches).
Most of the FF locations were reported to be distributed in the mountainous valleys, narrow alluvial coastal plains and alluvial fans at the foot of the mountainous areas (Figure 2). These FF locations were used as training datasets to investigate the spatial relationship between flash floods conditioning parameters and flash flooding occurrence, to learn the machine learning models, and to evaluate the performance and assess the accuracy of the three machine learning models.

3.2. Spatial Analysis and Construction of Flash Flood Conditioning Parameters

3.2.1. Construction of FFCPs

This study aims to map the susceptibly of flash floods and measure their magnitudes in an arid mountainous region with a minimum number of essential FFCPs to reduce errors and computational time and enhance the performance of the BRT, CART and NBT models [41,42]. Three types of FFCPs were chosen based on their degrees of influencing FF occurrences namely terrain and geohydrology. The terrain parameters include altitude, topographic slope, relief, topographic minimum curvature, while the geohydrology parameters include lithology, stream network (wadi courses), stream density, and distance from stream courses (Figure 5 and Figure 6). Thematic maps of FFCPs such as altitude, topographic slope, topographic relief, topographic curvature, and stream networks (wadi courses) were generated from ALOS DEM with a spatial resolution of 30 m using raster surface of 3D analysis and a hydrology of spatial analysis tools implemented in ArcGIS v.10.2 software. First, maps of altitude, slope, relief and topographic curvature were calculated by importing a 30 m DEM, converting a DEM into raster grid and applying raster surface to the raster grid. The range of altitude and relief from 100 m to 1800 m (m.s.l), the slope map classified into five classes: (i) 0°–5°, (ii) 5°–15°, (iii) 15°–30°, (iv) 30°–60°, and (v) >60° and the range of curvature from −200 to 50. Second, stream network was derived from a DEM using D8 algorithm implemented in hydrology tool. The algorithm starts by fill gaps (central pixel with no data) and determines into which neighboring pixel any water in a central will flow. After that, the flow direction and downhill slope of a central pixel to one of eight neighbors was calculated. Then, flow accumulation was calculated followed by deriving major stream networks using a threshold value of 45 [14]. This value was optimal to reveal the major stream networks in the study area. After that, drainage basins were calculated using the calculated flow direction theme. Third, distance from stream networks and the density of stream network were constructed using distance and density of spatial analyst tools implemented in the ArcGIS v. 10.2 software. Fourth, the lithological map was constructed from the Operational Landsat Imager (OLI) Landsat 8 acquired on 9 December 2019 (Path 160, rows 42 and 43) using maximum likelihood classifier (MLC) implemented in the Envi. v. 4.5 software. The MLC was trained using 200 training datasets collected from scanned geological maps at a scale of 50,000 collected from the UAE ATLAS. The ALOS DEM and Landsat 8 images were downloaded from the USGS Global Visualization Viewer (GloVis) (www.glovis.usgs.gov) portal.

3.2.2. Spatial Analysis

Altitude and topographic slope are the most important conditioning parameters for FF occurrences as they control water flow, flow direction, surface runoff and infiltration rate [25,42]. Sites at a lower altitude have a higher probability of FF where water flowing down from upper streams [43]. The topographic slope has a crucial influence on surface water flow, flow direction, runoff, infiltration rate and FF occurrence. As topographic slope increases, runoff potential increases resulting in FF [44]. Topographic curvature has a similar influence on FF occurrence. Sites with negative values for curvatures are zones of water accumulation and, thus, a higher probability of FF occurrence, while sites with positive values for curvature are zones of water dispersion, and thus have a lower probability occurrence of FF [25]. Lithology and its physical characteristics (e.g., porosity and permeability) strongly influence infiltration rate, runoff potential, stream network distribution, and thus FF occurrence [29]. Other FF conditioning parameters such as stream density and distance from streams also play a significant role in FF occurrence. As the distance from streams decreases, the probability of FF occurrence increases [45]. Factors such as aspect, land use/land cover (LULC), NDVI, topographic wetness index and index of the erosion power are secondary parameters and introduce bias and error during the modeling process and can be ignored [12,46,47]. These various FFCPs were chosen based on the geoenvironmental characteristics of the study area and used widely in this literature. These parameters can help in detecting flash flood-affected areas from the surrounding areas since flash flood occurrence is identified as varying greatly with the intensity of rainfall, altitude, slope and stream network [48,49].

3.3. Background and Theories of Models

3.3.1. Boosted Regression Tree (BRT)

The BRT is an ensemble technique and differs statistically from traditional methods. The BRT consists of machine learning and statistical techniques designed to improve the accuracy and the performance of a single model by fitting a group of models before combining these models for classification and prediction [50]. The BRT model merges regression from classification and regression tree (CART) and boosting techniques to produce a combined modeling. Boosting is a technique designed to enhance the performance of regression trees similar to model averaging [51]. However, the BRT implements a stepwise process, where the models are fitted to a subset of the training dataset. This subset used at every iteration of the model fit is stochastically chosen with no replacement.
The shrinkage parameter or learning rate determines the level of contribution for each tree to the growing model, while the number of nodes in a tree (tree complexity) decides whether interactions are fitted [52]. Then, these parameters determine the total number of trees required for prediction [53].
Elith et al. (2008) [53] described the model as the following steps:
1. Initialize weights to be equal wi = 1/n for m = 1 to iter classification Cm:
2. Fit classifier Cm to the weight data
3. Compute the weight or misclassification rate rm
4. Let the classifier weight
αm = log((1 − rm)/rm)
5. Recalculate weights
wi = wiexp(αmI(yi ≠ Cm))
6. Majority vote classification: sign [ΣMm−1 αmCm(x)]

3.3.2. Classification and Regression Trees (CART)

The CART is one of the most common algorithms for the classification of data. It is resistant to missing data, and its variables do not need to have a normal distribution [51,54]. It is a binary recursive partitioning procedure capable of processing continuous and nominal attributes as targets and predictors and was developed by Friedman (1975) [55], Breiman (1984) [56], and Breiman and Stone (1978) [57].
The algorithm has been successfully applied in medical applications to predict the value of a dependent variable based on the different values of independent variables [58], economics applications [59], photogrammetry [60], environmental protection [61], food science and chemistry [62,63], landslide susceptibility mapping [64], and groundwater potential mapping [65]. Classification trees are used when an independent variable is categorized, while regression trees are used when independent is continues and to predict its value (Figure 5 and Figure 6). The CART algorithm is designed as a sequence of trees where the ends are terminal nodes. It consists of three elements: (i) rules of splitting data at a node based on the value of one variable, (ii) stopping rules for deciding when a branch is terminal and can be split no more, and (iii) a prediction for the target variable in each terminal node (Figure 7). The major problem of building a valuable tree is finding the proper guidelines to prune the tree.
At the first stage, classification is created and leads to producing a tree with several branches. The number of branches of any tree depends on the degree of dispersion of data. The size of the tree depends on specific parameters such as the minimum population in the successive nodes, the minimum population of children, the maximum number of levels and the maximum number of nodes [51]. It is worthy to note that there is no relationship between the size of the tree and the accuracy of classification. The correct classification can be made by decreasing the overfiting of the training set.
The phase of cutting is created by generating the biggest possible trees and this process lies in reducing the total number of leaves and tending to increase the accuracy of classification. The final phase is the selection of a tree with a lower number of misclassifications and a higher accuracy. This higher accuracy can be released with the application of cross-validation using Equation (3):
RE(d) = 1/(N∑(i=1) (yi − d(xi))2
where yi is the number of points in the testing set (real variable), xi is the number of points in the testing set (variable classified with d model), N is the number of cases in a testing set. The results of the predicted model were evaluated using a set of testing samples. The measure of the cross-validation Rα(T) is a linear dependence between the complexity of the tree and the cost of misclassifications Equation (4) [51].
Rα(T) = R(T) + αT ⬄ α = Rα(T) − R(T)/|T|
where Rα(T) is the cost-complexity measure, R(T) is the cost of misclassifications, |T| is the complexity of tree measures as the number of terminal nodes in the tree, a parameter of tree complexity (assumes values from 0 for a maximal tree to 1 for a minimal tree).
The produced regression rule set was then applied to all FFCPs to map flash flood susceptibility. It is worthily of note that the dependence (complexity of the tree) and accuracy of classification should be taken into consideration. The low complexity of the tree usually leads to the low accuracy of classification.
The output of CART is a hierarchical binary tree which subdivides the prediction space into several regions (Rm) where the response factors have similar values (≡ am) based on Equation (5):
f ≅ am; ∀x ∈ Rm

3.3.3. Naive Bayes Tree (NBT)

Naive Bayes (NB) is a machine learning classifier that creates a probability-based model. It works based on Bayes Theorem, which is known as Naive Bayes. The NB uses a decision tree (DT) for its structure and organizes an NB model on every leaf node of the constructed DT [66]. The NBT exhibits a significant classification performance and accuracy [67,68].
During the NB process, the impact of an attribute value on a specific class is independent of the value of another attribute and known as class conditional independence. This conditional independence of NB makes the datasets to train quicker and it considers all the vectors as independent and applies the Bayes rule [69]. Bayes role can be explained as follows (Equation (6):
P(A|B) = P(B|A) P(A)/P(B)
where:
P(A|B) = conditional probability of A given B
P(B|A) = conditional probability of A given B
P(A) = probability of event A
P(B) = probability of event B
The model starts by estimating the probability of each class in the model, calculating the covariance and variance matrix, and building the discriminate function for each class [70,71,72].

3.4. Optimal Model Parameterisation and Flash Flood Susceptibility Mapping

As a first step, the CART, BRT and NB models were fitted in SATISTICA v. 7 [73], Salford system [74,75], and in R (R Development Core Team 2006) v.3.0.2 [76], implementing gbm, dismo, rpart, and random forest packages [77]. These tools have a stochastic gradient boosting tree which is widely used for regression problems related to predicting and mapping continues dependent variables [73]. After that, the setting and optimizing of all parameters was performed. These parameters were; learning rate, the number of additive trees, the proportion of sub-sampling, and so forth.
Here, the optimal value for the learning rate was set as 0.1, additive trees were 185, and the maximum size of the tree was five. These values may lead to precise results accuracy [74]. In this study, the random point’s values have been extracted from each variable of FFCPs for the presence and absence condition of the FF. After that, all three machine learning models were then run based on the mechanism of the open-source tools. Using these tools, FFSM was calculated for each pixel in the thematic maps of FFCPs and then converted into text files. Finally, these text and dbase files were imported into SPSS v.25 to evaluate the models’ performance and generate FFSM in GIS environment of ArcGIS v.10.2 software.
During the prediction processing, the models used FFCPs and the regression tree separates the FFCPs into two groups [78,79]. A group such as distance from streams, altitude, and slope in the upper part of the regression tree indicates an approximate area with a higher probability occurrence of FF. Another group, such as altitude, slope, and topographic curvature in the lower part of the regression tree allowed recognition areas of a higher probability of FF occurrence. Among several interval methods, the quantile method, which is used widely in the literature, was chosen to classify FFSM [12,14,36]. The produced FFSM was then classified into four classes namely low, moderate, high, and very high.

3.5. Evaluation of the Models Performance

To evaluate the models’ performance, we used 61 FF locations. The datasets were divided into 43 (70%) for model training and 18 (30%) for the model validation. These datasets were classified and selected randomly using the Hawth’s Tool implemented in the ArcGIS v. 10.2 Software. We calculated the accuracy metrics for each model. Each metric includes accuracy, precision, recall and F1 score. The F1 score was found to the best technique and used widely in literature [13,14,80]. The F1 score was calculated based on four parameters, namely true positive (TP), true-negative (TN), false-positive (FP), and false-negative (FN) using the following equations from 7–11:
Accuracy = TP + (TN/TP) + FP + FN + TN
Kappa = po − pe/(1 − pe)
where po is the observed agreement ratio, and pe is the expected agreement
Precision = TP/(TR + FP)
Recall = TP/(TP + FN)
F1 = 2 × precision recall/(precision + recall)
where TP is the true-positive; FP is the false-positive and FN is the false-negative.
The performance of SVM and SAM were evaluated using the open-source R 4.0.0 software. Further validation was performed using the receiver operating characteristics (ROC) curve, which is used widely in the literature due to its simplicity, easiness and higher accuracy [81]. The curve has been successfully used by several researchers in several applications such as groundwater potential mapping [82], and land subsidence susceptibility mapping [12]. The obtained prediction FF maps sometimes contain errors. These errors sometimes come from the deficiency of the FFCPs quality and the structure of the models [46,83].
The accuracy of the produced prediction maps was measured using the area under the curve (AUC) [84]. The AUC ranges from 0 to 1. AUC with a value of 1 indicating a good prediction, and a value of 0 indicating the model is not efficient and cannot predict FF occurrence. Both the success and prediction rates were created to assess the accuracy of the FFSM [85]. The value of AUC can be estimated via the following equation [86]
AUC = Σ (TP + ΣTN/(P + N))
where TP (true positive) and TN (true negative) are the numbers of pixels that are correctly classified. P is the total number of pixels with torrential phenomena, and N is the total number of pixels of no flash floods.

3.6. Geohydrological Model for FFMI and Filling the Gaps in MLC Maps

Although ensemble-based machine learning models have been used widely in FFS mapping due to their greater accuracy, these models still have some limitations regarding FFCPs. These include the length of the basin, basin area, the gradient of each basin, alluvial plain width, and mean slope. These new parameters are very important in measuring the FF magnitude. Here, we first delineated drainage basins from a DEM using a hydrological tool implemented in the Arc GIS v. 10.2 Software. After that, each basin was considered and treated as a separate FF zone and its magnitude was measured by calculating the following parameters (Figure 8 and Table 1):
(i) Calculating the length of each basin (Lb)
(ii) Calculating the relief for each basin (Bh)
relief = Bh = hmax − hmin (the difference between the maximum and minimum heights)
(iii) Calculating the gradient of each basin (G°) using the following equation
Gradient = (Bh/Lb) × 60
(iv) Calculating the area for each basin (A)
A = basin area (km2)
(v) Calculating the alluvial plain width (Aw) for each basin manually in a GIS
(vi) Calculating the mean slope (Ms) for each basin using a moment statistic
(vii) Calculating FF magnitude for each basin with the following equation;
Flash Flood magnitude = Ms/ln (A/G°)

4. Results and Discussion

4.1. Evaluation of the Models Performance and Validation

Visual inspection shows that there are some differences among the FFSM maps produced using machine learning models. Thus, it is important to evaluate model performance and assess the prediction accuracy. The results from the evaluation of the model performance show that the BRT model had the highest accuracy, followed by the CART and the NB models. The BRT yields an F1 score value of more than 0.91 for all FFS classes, followed by the CART with an F1 score value of more than 0.90 for high and very high classes (Figure 9).
The NB had the lowest F1 score for all FF classes. Thus, the validation results confirmed a positive agreement between the observed and predicted values for the BRT and CART models. Additionally, the slight difference between the F1 score of the BRT and the CART models is due to the gap between the two models and is not statistically different [87]. The BRT model offers reliable information regarding the FF to be predicted [42]. The BRT has the boosting approach that can employ an existing AI method and has the dual advantage of boosting and decision trees [87]. Further quantitative validation using the ROC curve was performed to examine the reliability of the obtained FFSM [88]. Similar to the F1 score, the BRT model has the highest AUC value (0.92), followed by the CART model (0.90) and the NB model (0.79). The high performance of the BRT is because it combines the CART with a boosting algorithm (Figure 10).

4.2. Spatial Analysis and Flash Floods Susceptibility Mapping

The results of the spatial analysis show that the extreme FF events had occurred at narrow alluvial plains of the mountainous and coastal areas. These areas are characterized with steep slopes, high relief, surface run-off and high density of streams. The higher density of streams reflects rocks with a lower rate of permeability that has a higher probability of FF occurring. The most important FFCPs affecting FF occurrence altitude and slope (Figure 5a,b). Both parameters strongly influence relief, topographic curvature (Figure 5c,d), soil moisture and surface run-off. For topographic curvature, convex classes (>0) have a very low influence on FF occurrence. Concave slopes (<0) had the strongest impact on FF occurrence (Figure 5c). About 90% (40 FF events) of the past FF events had occurred at an elevation from 300 m to 1400 m and slopes between 10° to 15° (Figure 5a). Another important FFP affecting flood was lithology. For the lithology factor, the upper streams are dominant by igneous and metamorphic rocks, while the lower streams are dominant by alluvial deposits. Most of the past FF events had occurred in the alluvial plains and fans (flooded plains) at the foot of the mountainous areas (igneous and metamorphic rocks) (Figure 6a). For distance from streams and streams density, the highest number of the past FF events had occurred in areas within 1000 m from the major stream networks (wadi courses) and characterized by a low density of streams (Figure 6b,c).
Parameters such as LULC and aspect and plan curvature have no significant contribution to the modeling process and could affect the accuracy of the model’s predictions [13,44,89]. These parameters should be ignored and not considered in the modeling process since the aspect is already calculated during the extraction of stream networks, and the area is characterized by low urban development [13,42].
Maps of FFSMs were constructed by dividing the study area into separated pixels. Each pixel was categorized as a flood and non-flood class. Thus, the FFS index for each map was calculated for all pixels and each pixel was assigned a unique susceptibility index [12,13,36]. The testing of several classification methods such as equal interval, geometrical interval, natural break and quantile shows that the quantile and interval methods were the most appropriate method to classify flooded and non-flooded areas, respectively. This finding agrees well with similar studies applied by Khosravi et al. (2016) [36] who tested several classification methods for different susceptibility mapping. Susceptibility maps of FF produced using BRT, CART and NBT model are shown in Figure 11. These susceptibly indices were categorized into four classes intervals using the quantile technique, which is used widely in the literature [12,36,90]. The produced susceptibly classes were recognized namely very high, high, moderate and low construct FFSMs (Figure 11).
The maps demonstrate that the high and very high susceptibility classes are commonly located in wadi courses and alluvial plains of the mountainous areas in the east and north. Some portions of very high and high classes are located at the foot of mountainous areas. About 54% (3196.4 km2) of the total area was classified as high and very high classes of FF, 19.3% (1136 km2) was classified as moderate susceptibility classes of FF, and 26.5% (1561 km2) as low class susceptibility of FF. The effectiveness of the proposed MCL models was confirmed by the highest F1 and AUC values than the individual MCL model.

4.3. Geohydrological Model for FFMI and Filling the Gaps in MCL Maps

Although the BRT model yields the highest performance, the geographical and spatial variability of the valley depth and alluvial plain width parameters have not been taken into consideration. In this study, the FF magnitude index (FFMI) was calculated using a set of new terrain parameters for each derived basin (Table 1). These parameters include basin area (A) (Figure 12a) the length of the basin (Lb) (Figure 12b), relief (Bh) (Figure 12c), alluvial plain width (Aw) (Figure 13a), gradient (G°) (Figure 13b), and mean slope (Ms) (Figure 13c).
Figure 12a shows that the area is divided into seven basins (zones) of flash flood and can be divided into two types. The first type is narrow coastal zones such as RAK in the northwest, Masafi, Rul Dadanh-Dibba and Fujairah-Kalba in the east. The second type is wide inland basins (zones) such as Falahyeen and Al Dhaid in the west and Hatta-Houylate in the south (Figure 1, Figure 2 and Figure 12a). Except for Al Dhaid and Falaheen basins, all basins are small in area, short in length, drained by dendritic streams in shape and narrow alluvial plains. These zones and their adjoining areas have high gradient angles ranging from 10° to 33°, high relief values of more than 900 m, mean slope of than 30°, and an alluvial plain width of less than 5 km (Figure 12 and Figure 13). Lithologically, all upper streams are dominated by the igneous, metamorphic, and carbonate rocks, while the lower streams are dominated by alluvial deposits. These parameters directly influence the magnitude of the destruction of the FF and have a greater impact on the occurrence of FF in an arid region. For example, a basin (zone) with a higher relief and runoff potential indicates rocks with lower permeability, steeper slopes, relief, and high runoff potential in a basin with a narrow alluvial plain, which can cause susceptibility to floods [91].
Figure 14a shows the modified map of FF produced using the proposed hybrid approach. The map shows different FF zones. Each zone has its own FF magnitude. The estimated FF magnitude values for the basins of RAK and Massafi were 3.24 and 3, respectively (Table 1 and Figure 14a). Villages, roads and farms in these basins were severely affected zones. They cover an area of about 1379 km2 (23.4%). Rol Dadnah and Fujairah-Kalba basins that cover an area of 1055.6 km2 (17.9%) and have high FF magnitude values of 2.96 and 2.71, respectively. Hatta-Houylate has a moderate FF magnitude of 1.11, while Falahyeen and Al Dhaid have FF magnitude values of 0.57 and 0.16, respectively.
To validate the produced FFMI, the past FF events were draped over the FFMI and spatial analysis was performed. The results showed that most of the past FF events (40 FF events) had occurred in high and very high FF susceptibility zones. Further analysis was performed by draping the existing infrastructures and agricultural area over the FFIM shows that most of the villages and farms in mountainous areas and the RAK are located in areas at a higher risk. This fact is acceptable since all settlements, farms and roads have been constructed in the high and very high susceptible zones.
The proposed approach permits that FFCPs be updated at any time, as new parameters become available.

5. Discussion

5.1. Evaluation of the Models Performance and Validation

In this study, a hybrid approach, which integrates machine learning and geohydrological models, was modified to map FF susceptible areas and measure their FF magnitude in an arid mountainous region. We first used three machine learning models to map the susceptibility of natural phenomena with nonlinear relationships and without the need for prior elimination of statistical supposition and data transformation [12,92,93]. These types of models can fit complex nonlinear relationships between FF locations and conditioning parameters and their efficiency compared based on accuracy matrices (precision, recall and F1 score) and AUC-ROC [14].
The results demonstrated that the BRT model had the highest performance, while NBT a higher accuracy comparing with NBT [53]. This finding is consistent with Rahmati et al. (2020) [94] who used a machine learning approach for spatial modeling of agricultural droughts. They concluded that the BRT and CART models showed the best performance and prediction accuracy compared with NBT and linear supervised classifiers. Our findings also agree well with Naghibi et al. (2016) [65], who concluded that the BRT model produced the best prediction results followed by the CART and RF models. These machine learning, used widely in the literature, were applied due to their simplicity in description, their accuracy, and straightforwardness of interpretation [7,8,13,14,22,23,29,30,31,33,53,94,95]. However, limited numbers have been applied to FF susceptibility mapping using a hybrid approach, which integrates machine learning models and morphological and geohydrological parameters to map FF susceptibly and measure its magnitude for each basin the FFSM.

5.2. Spatial Analysis and Flash Floods Susceptibility Mapping

FF is one of the main destructive phenomena that occur in mountainous areas and narrow alluvial coastal areas, especially in the NUAE. FF susceptibility mapping using remote sensing and MCL algorithms is considered as a crucial step to reduce the destructive impact of any future FF event [36,80,96]. Spatial analysis showed that most of the built-up and agricultural areas of the Emirates of RAK in the northwest and Fujiarah in the East (95%), and some parts of the Emirates of Ajman and Sharjah (20%) are located in high and very high susceptible zones. Thus, most of roads, dams, farms, and the human population are highly susceptible FF because they are located in wadi courses of the mountainous areas and at the foot of the mountainous areas. These areas receive intensive rainfall due to the impact of climate change [38]. In these zones, a proper urban planning scheme is very important to reduce risk hazard of any future FF event (Bathrellos et al., 2017).
Tremendous numbers of previous studies proposed a combination of MCL models for FFS mapping. They built susceptibility maps using several conditioning factors that are relatively complex [28,36,38,86,96]. Other studies have shown that intensive precipitation, LULC and geohydrology parameters are important factors controlling FF occurrence [28,36,96]. Further studies have shown that factor such as human activities is a significant in FF occurrence [25,94]. These factors such as LULC and human activities could not consider as significant factors in the study area due to low population and intensive human activities. Additionally, the obtained FFSMs using MCL are, in realty, altitude and/or slope map. Thus, it is important to modify geohydrological model and a hybrid approach.

5.3. Geohydrological Model for FFM Indexing and Filling the Gaps in MLC Maps

To measure FF magnitude and fill the gaps in the MCL maps, it is important to a hydrological model. Until now, there is no standard rule to choose FFCFs, flood and non-flood locations. Here, the result obtained using the proposed approach and new FFCPs is consistent with the constructed FF inventory map and demonstrated that the proposed approach was able to map susceptible FF and measure their magnitudes in an arid region and much more accurately and reliably compared to ensemble machine learning approaches that are widely used to susceptibility map groundwater potentiality [82], land subsidence [12], landslides [3,42,85], and flash floods [3,23,26,29,30,31]. The obtained susceptibility maps using MCL can be upgraded and re-categorized using the proposed approach and demonstrated that the approach was able to create a satisfactory FFM. The result shows that the highest number of the past FF events in the study area are commonly occurred in the major mountainous streams (wadi courses) and the narrow coastal strip in the east and in the northwest. These areas are lowlands covered by alluvial deposits, located at the foot of the Oman mountains and characterized by the gentle slope.
Based on the new map of FFMI and its related infrastructures map (Figure 14b), about 153.34 km in length of mountainous roads and those at the foot of mountainous areas are dangerous and deadly roads. Roads of residential areas are also dangerous and had a higher probability to destroy (Figure 14b). In Ras Al Khaimah (RAK), one woman was crushed to death after a wall collapsed during a violent storm (NCM, 2020). In Ghalilah and Al Fahlain villages of the RAK, flash floods destroyed roads, farms and flooded the village graveyard (Figure 1). The risk of damage can be reduced by constructing valley dams and a real-time alert system in the mountainous areas. The existing human settlements in the valley mouth should be shifted to the terrain at a lower elevation with a very gentle slope. Here, the produced FFSM and FFMI can be used as a reference for decision-makers and urban planners.
The results of the proposed approach permit a better understanding of the natural hazard setting of the study area for the first time. The results also facilitate the detection of sites of a higher probability of FF occurrence help identification of infrastructures that are located at high risk. The use of geohydrological approach can be used to fill the gaps in the FFSMs obtained using MCL models and represents an effective approach for FFSM and measuring FF magnitude, particularly in the NUAE, which has not been investigated previously. This finding agrees well Chen et al. (2019) [97] who concluded that the superiority of hybrid models. However, some limitations have been reported during the modeling process. These limitations include the spatial resolution and number of FF conditioning parameters as well as the optimal parameterization of the machine learning algorithms [12,13,95]. Therefore, future work will focus on FF susceptibility mapping using new FFC parameters such as alluvial plain width, the depth of the mountainous valley, and the gradient of the basin. Future work will focus on constructing a real-time meteorological system that is needed to predict areas with a higher FF occurrence. Plantation of Prosopis Cineraria forests and merging steel wedges and screens on the wadi slopes are also needed to reduce runoff potential.

6. Conclusions

In this study, a hybrid approach that integrates machine learning (the BRT, CART and NBT) and geohydrological models was applied for FF susceptibility mapping and constructing FFMI. The proposed approach was applied, for the first time, to the NUAE. Eight FFCPs, namely; altitude, topographic slope, topographic curvature, relief, streams density, lithology, and distance from streams, were chosen for FFSM. The parameters were selected based on their level of influencing FF occurrence, the geo-environmental characteristics of the study area, the geological background of the authors, and those used widely in this literature. Parameters such as LULC, aspect, plan curvature, and NDVI were ignored since the aspect (flow direction) already calculated during stream network extraction, and the study area is characterized by low population, human activity, and large vegetation cover.
The performance of the machine learning models was evaluated by calculating accuracy metrics using the F1 score for each model and ROC curve. The results showed that the BRT had the highest performance followed by the NBT and CART models. The produced FFSM using the BRT was modified by applying a geohydrological approach, and results showed that the area consists of seven FF zones. Each FF zone has its geohydrological characteristics and FF magnitude. The highest FF magnitude was found to be in the zones of the RAK and Masafi, Rul Dadna, and Fujairah-Kalaba, while the lowest FF magnitude was found to be in the zones of Al Dhaid and Falahyeen in the west. These magnitudes can be further enhanced by applying the proposed approach to sub-basins using remote sensing data with a higher spatial resolution. New FFCPs such as alluvial plain width, stream depth, basin gradient and mean slope can be considered in any future study, especially in an arid region. As a conclusion, the proposed approach and new FFCPs from this study demonstrated the superiority of hybrid models, and the obtained FFSMs can assist urban planners, geohazard specialists and decision-makers to reduce the risk of the FF in an arid region.

Author Contributions

Data providing, M.M.; supervision and project administration T.A.; writing—original draft and data analysis, S.E. All authors have read and agreed to the published version of the manuscript.

Funding

The research has received funding under financial grant SCRI 18 Grant EN0- 284.

Acknowledgments

The authors would like to thank the American University of Sharjah for supporting this research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kron, W. Keynote lecture: Flood risk = hazard × exposure × vulnerability. In Flood Defence 2002; Science Press, New York Ltd.: New York, NY, USA, 2002; pp. 82–97. [Google Scholar]
  2. Yin, J.; Yu, D.; Yin, Z.; Liu, M.; He, Q. Evaluating the impact and risk of pluvial flash flood on intra-urban road network: A case study in the city center of Shanghai, China. J. Hydrol. 2016, 537, 138–145. [Google Scholar] [CrossRef] [Green Version]
  3. Casale, R.; Margottini, C. Floods and Landslides: Integrated Risk Assessment: Integrated Risk Assessment; with 30 Tables; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
  4. Kohavi, R. Scaling up the accuracy of naive-bayes classifiers: A decision-tree hybrid. KDD 1996, 96, 202–207. [Google Scholar]
  5. Aksoy, H.; Kirca, V.S.O.; Burgan, H.I.; Kellecioglu, D. Hydrological and hydraulic models for determination of flood-prone and flood inundation areas. Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 137–141. [Google Scholar] [CrossRef] [Green Version]
  6. Al-Hashemi, H.M.B.; Al-Amoudi, O.S.B. A review on the angle of repose of granular materials. Powder Technol. 2018, 330, 397–417. [Google Scholar] [CrossRef]
  7. Elkhrachy, I. Flash Flood Hazard Mapping Using Satellite Images and GIS Tools: A case study of Najran City, Kingdom of Saudi Arabia (KSA). Egypt. J. Remote Sens. Space Sci. 2015, 18, 261–278. [Google Scholar] [CrossRef] [Green Version]
  8. Elshorbagy, A.; Corzo, G.; Srinivasulu, S.; Solomatine, D.P. Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology—Part 2: Application. Hydrol. Earth Syst. Sci. 2010, 14, 1943–1961. [Google Scholar] [CrossRef] [Green Version]
  9. Folke, C. Resilience: The emergence of a perspective for social ecological systems analyses. Glob. Environ. Change 2006, 16, 253–267. [Google Scholar] [CrossRef]
  10. Santangelo, N.; Santo, A.; Di Crescenzo, G.; Foscari, G.; Liuzza, V.; Sciarrotta, S.; Scorpio, V. Flood susceptibility assessment in a highly urbanized alluvial fan: The case study of Sala Consilina (southern Italy). Nat. Hazards Earth Syst. Sci. 2011, 11, 2765–2780. [Google Scholar] [CrossRef] [Green Version]
  11. Wang, Y.; Hong, H.; Pourghasemi, H.R.; Li, S.; Pamucar, D.; Gigović, L.; Drobnjak, S.; Bui, D.T.; Duan, H. A Hybrid GIS Multi-Criteria Decision-Making Method for Flood Susceptibility Mapping at Shangyou, China. Remote Sens. 2018, 11, 62. [Google Scholar] [CrossRef] [Green Version]
  12. Elmahdy, S.I.; Mohamed, M.M.; Ali, T.A.; Abdalla, J.E.-D.; Abouleish, M. Land subsidence and sinkholes susceptibility mapping and analysis using random forest and frequency ratio models in Al Ain, UAE. Geocarto Int. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
  13. Elmahdy, S.I.; Mohamed, M.M.; Ali, T. Land Use/Land Cover Changes Impact on Groundwater Level and Quality in the Northern Part of the United Arab Emirates. Remote Sens. 2020, 12, 1715. [Google Scholar] [CrossRef]
  14. Elmahdy, S.I.; Ali, T.A.; Mohamed, M.M.; Howari, F.M.; Abouleish, M.; Simonet, D. Spatiotemporal Mapping and Monitoring of Mangrove Forests Changes From 1990 to 2019 in the Northern Emirates, UAE Using Random Forest, Kernel Logistic Regression and Naive Bayes Tree Models. Front. Environ. Sci. 2020, 8, 102. [Google Scholar] [CrossRef]
  15. Quinn, P.; Beven, K.; Chevallier, P.; Planchon, O. The prediction of hillslope fow paths for distributed hydrological modeling using digital terrain models. Hydrol. Process. 1991, 5, 59–79. [Google Scholar] [CrossRef]
  16. Fortin, J.P.; Turcotte, R.; Massicotte, S.; Moussa, R.; Fritzback, J.; Villeneuve, J.P. Distributed watershed model compatible with remote sensing and GIS data, I: Description of model. J. Hydrol. Eng. 2001, 6, 91–99. [Google Scholar] [CrossRef]
  17. Jayakrishnan, R.; Srinivasan, R.; Santhi, C.; Arnold, J.G. Advances in the application of the SWAT model for water resources management. Hydrol. Process. 2005, 19, 749–762. [Google Scholar] [CrossRef]
  18. Bahremand, A.; De Smedt, F.; Corluy, J.; Liu, Y.B.; Poórová, J.; Velcická, L.; Kunikova, E.; Smedt, F. WetSpa Model Application for Assessing Reforestation Impacts on Floods in Margecany–Hornad Watershed, Slovakia. Water Resour. Manag. 2006, 21, 1373–1391. [Google Scholar] [CrossRef]
  19. Fenicia, F.; Kavetski, D.; Savenije, H.H.G.; Clark, M.P.; Schoups, G.; Pfister, L.; Freer, J. Catchment properties, function, and conceptual model representation: Is there a correspondence? Hydrol. Process. 2014, 28, 2451–2467. [Google Scholar] [CrossRef]
  20. Smith, D.I.; Ward, R. Floods: Physical Processes and Human Impacts; John Wiley and Sons Ltd.: Chichester, UK, 1998. [Google Scholar]
  21. Toth, E.; Brath, A.; Montanari, A. Comparison of short-term rainfall prediction models for real-time flood forecasting. J. Hydrol. 2000, 239, 132–147. [Google Scholar] [CrossRef]
  22. Şarlak, N. Flood Frequency Estimator with Nonparametric Approaches in Turkey. Fresenius Environ. Bull. 2012, 21, 1083–1089. [Google Scholar]
  23. Dou, J.; Shirzadi, A.; Ghaderi, K.; Omidavr, E.; Al-Ansari, N.; Clague, J.J.; Geertsema, M.; Khosravi, K.; Amini, A.; Bahrami, S.; et al. Flood Detection and Susceptibility Mapping Using Sentinel-1 Remote Sensing Data and a Machine Learning Approach: Hybrid Intelligence of Bagging Ensemble Based on K-Nearest Neighbor Classifier. Remote Sens. 2020, 12, 266. [Google Scholar] [CrossRef] [Green Version]
  24. Yalcin, A.; Yalçın, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
  25. Elmahdy, S.I.; Mohamed, M.M. Probabilistic frequency ratio model for groundwater potential mapping in Al Jaww plain, UAE. Arab. J. Geosci. 2015, 8, 2405–2416. [Google Scholar] [CrossRef]
  26. Bui, D.T.; Tsangaratos, P.; Ngo, P.T.; Pham, T.D.; Pham, B.T. Flash flood susceptibility modeling using an optimized fuzzy rule based feature selection technique and tree based ensemble methods . Sci. Total Environ. 2019, 668, 1038–1054. [Google Scholar] [CrossRef] [PubMed]
  27. Mohammady, M.; Pourghasemi, H.R.; Amiri, M. Assessment of land subsidence susceptibility in Semnan plain (Iran): A comparison of support vector machine and weights of evidence data mining algorithms. Nat. Hazards 2019, 99, 951–971. [Google Scholar] [CrossRef]
  28. Bui, D.T.; Hoang, N.-D.; Pijush, S. Spatial pattern analysis and prediction of forest fire using new machine learning approach of Multivariate Adaptive Regression Splines and Differential Flower Pollination optimization: A case study at Lao Cai province (Viet Nam). J. Environ. Manag. 2019, 237, 476–487. [Google Scholar] [CrossRef]
  29. Rahmati, O.; Pourghasemi, H.R.; Zeinivand, H. Flood susceptibility mapping using frequency ratio and weights-of-evidence models in the Golastan Province, Iran. Geocarto Int. 2015, 31, 42–70. [Google Scholar] [CrossRef]
  30. Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Dou, J.; Revhaug, I.; Prakash, I.; Bui, D.T. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total. Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
  31. Zhao, G.; Pang, B.; Xu, Z.; Yue, J.; Tu, T. Mapping flood susceptibility in mountainous areas on a national scale in China. Sci. Total Environ. 2018, 615, 1133–1142. [Google Scholar] [CrossRef]
  32. Bui, D.T.; Ngo, P.-T.T.; Pham, T.D.; Jaafari, A.; Minh, N.Q.; Hoa, P.V.; Samui, P. A novel hybrid approach based on a swarm intelligence optimized extreme learning machine for flash flood susceptibility mapping. Catena 2019, 179, 184–196. [Google Scholar] [CrossRef]
  33. Bui, D.T.; Hoang, N.-D.; Martínez-Álvarez, F.; Ngo, P.-T.T.; Hoa, P.V.; Pham, T.D.; Samui, P.; Costache, R. A novel deep learning neural network approach for predicting flash flood susceptibility: A case study at a high frequency tropical storm area. Sci. Total Environ. 2020, 701, 134413. [Google Scholar] [CrossRef]
  34. Chen, X.; Ahmadi, M.H.; Busari, A. A comparative study of population-based optimization algorithms for downstream river flow forecasting by a hybrid neural network model. Eng. Appl. Artif. Intell. 2015, 46, 258–268. [Google Scholar] [CrossRef]
  35. Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and Naïve Bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. Catena 2016, 145, 164–179. [Google Scholar] [CrossRef]
  36. Khosravi, K.; Pourghasemi, H.R.; Chapi, K.; Bahri, M. Flash flood susceptibility analysis and its mapping using different bivariate models in Iran: A comparison between Shannon’s entropy, statistical index, and weighting factor models. Environ. Monit. Assess. 2016, 188, 656. [Google Scholar] [CrossRef] [PubMed]
  37. Al-Rashed, M.F.; Sherif, M.M. Water Resources in the GCC Countries: An Overview. Water Resour. Manag. 2000, 14, 59–75. [Google Scholar] [CrossRef]
  38. Sherif, M.; Almulla, M.; Shetty, A.; Chowdhury, R. Analysis of rainfall, PMP and drought in the United Arab Emirates. Int. J. Clim. 2014, 34, 1318–1328. [Google Scholar] [CrossRef]
  39. Giri, S.; Singh, A.K. Human health risk assessment via drinking water pathway due to metal contamination in the groundwater of Subarnarekha River Basin, India. Environ. Monit. Assess. 2015, 187, 63. [Google Scholar] [CrossRef] [PubMed]
  40. The Master Plan Study on the Groundwater Resources Development for Agriculture in the Vicinity of Al Dhaid in the UAE; Final Report; JICA International Cooperation Agency: Tokyo, Japan, 1996.
  41. Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2015, 13, 361–378. [Google Scholar] [CrossRef]
  42. Pham, B.T.; Bui, D.T.; Dholakia, M.B.; Prakash, I.; Pham, H.V. A Comparative Study of Least Square Support Vector Machines and Multiclass Alternating Decision Trees for Spatial Prediction of Rainfall-Induced Landslides in a Tropical Cyclones Area. Geotech. Geol. Eng. 2016, 34, 1807–1824. [Google Scholar] [CrossRef]
  43. Fernández, D.; Lutz, M. Urban flood hazard zoning in Tucumán Province, Argentina, using GIS and multicriteria decision analysis. Eng. Geol. 2010, 111, 90–98. [Google Scholar] [CrossRef]
  44. Costache, R.; Pham, Q.B.; Sharifi, E.; Linh, N.T.; Abba, S.I.; Vojtek, M.; Khoi, D.N. Flash-flood susceptibility assessment using multi-criteria decision making and machine learning supported by remote sensing and gis techniques. Remote Sens. 2020, 12, 106. [Google Scholar] [CrossRef] [Green Version]
  45. Glenn, E.P.; Morino, K.; Nagler, P.L.; Murray, R.; Pearlstein, S.; Hultine, K.R. Roles of saltcedar (Tamarix spp.) and capillary rise in salinizing a non-flooding terrace on a flow-regulated desert river. J. Arid Environ. 2012, 79, 56–65. [Google Scholar] [CrossRef]
  46. Loosvelt, L.; Peters, J.; Skriver, H.; Lievens, H.; Van Coillie, F.M.; De Baets, B.; Verhoest, N.E.C. Random Forests as a tool for estimating uncertainty at pixel-level in SAR image classification. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 173–184. [Google Scholar] [CrossRef]
  47. Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of GIS-based data driven random forest and maximum entropy models for groundwater potential mapping: A case study at Mehran Region, Iran. Catena 2015, 137, 360–372. [Google Scholar] [CrossRef]
  48. Santo, A.; Di Crescenzo, G.; Del Prete, S.; Di Iorio, L. The Ischia island flash flood of November 2009 (Italy): Phenomenon analysis and flood hazard. Phys. Chem. Earth 2012, 49, 3–17. [Google Scholar] [CrossRef]
  49. Nijzink, R.C.; Samaniego, L.; Mai, J.; Kumar, R.; Thober, S.; Zink, M.; Schafer, D.; Savenije, H.H.; Hrachowitz, M. The importance of topography-controlled sub-grid process heterogeneity and semi-quantitative prior constraints in distributed hydrological models. Hydrol. Earth Syst. Sci. 2016, 20, 1151–1176. [Google Scholar] [CrossRef] [Green Version]
  50. Schapire, R.E. The Boosting Approach to Machine Learning: An Overview. In Nonlinear Estimation and Classification; Springer: New York, NY, USA, 2003; pp. 149–171. [Google Scholar]
  51. Gordon, A.D.; Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees. Biometrics 1984, 40, 874. [Google Scholar] [CrossRef] [Green Version]
  52. Chen, W.; Li, Y.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Bian, H. Groundwater Spring Potential Mapping Using Artificial Intelligence Approach Based on Kernel Logistic Regression, Random Forest, and Alternating Decision Tree Models. Appl. Sci. 2020, 10, 425. [Google Scholar] [CrossRef] [Green Version]
  53. Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
  54. Rothwell, J.J.; Futter, M.; Dise, N.B. A classification and regression tree model of controls on dissolved inorganic nitrogen leaching from European forests. Environ. Pollut. 2008, 156, 544–552. [Google Scholar] [CrossRef]
  55. Friedman, L.A. The Measure of a Successful Information Storage and Retrieval System. In Perspectives in Information Science; Springer: Dordrect, The Netherlands, 1975; pp. 379–408. [Google Scholar]
  56. Breiman, L.; Jerome, F.; Charles, J.S.; Richard, A.O. Classification and Regression Trees; Wadsworth Int. Group: Dordrecht, The Netherlands, 1984; Volume 37, pp. 237–251. [Google Scholar]
  57. Breiman, L.; Stone, C.J. Parsimonious Binary Classification Trees; California Technical Report TSCCSD-TN; Technology Service Corporation: Santa Monica, CA, USA, 1978; Volume 4. [Google Scholar]
  58. Türe, M.; Tokatli, F.; Kurt, I.; Tokatlı, F. Using Kaplan–Meier analysis together with decision tree methods (C&RT, CHAID, QUEST, C4.5 and ID3) in determining recurrence-free survival of breast cancer patients. Expert Syst. Appl. 2009, 36, 2017–2026. [Google Scholar] [CrossRef]
  59. Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. TIST 2011, 2, 1–27. [Google Scholar] [CrossRef]
  60. Yang, L.; Xian, G.; Klaver, J.M.; Deal, B. Urban Land-Cover Change Detection through Sub-Pixel Imperviousness Mapping Using Remotely Sensed Data. Photogramm. Eng. Remote Sens. 2003, 69, 1003–1010. [Google Scholar] [CrossRef]
  61. Smeti, E.M.; Thanasoulias, N.; Lytras, E.; Tzoumerkas, P.; Golfinopoulos, S. Treated water quality assurance and description of distribution networks by multivariate chemometrics. Water Res. 2009, 43, 4676–4684. [Google Scholar] [CrossRef] [PubMed]
  62. Hazir, M.H.M.; Shariff, A.; Amiruddin, M.D.; Ramli, A.R.; Saripan, M.I. Oil palm bunch ripeness classification using fluorescence technique. J. Food Eng. 2012, 113, 534–540. [Google Scholar] [CrossRef]
  63. Chudzinska, M.; Barałkiewicz, D. Application of ICP-MS method of determination of 15 elements in honey with chemometric approach for the verification of their authenticity. Food Chem. Toxicol. 2011, 49, 2741–2749. [Google Scholar] [CrossRef]
  64. Vorpahl, P.; Elsenbeer, H.; Märker, M.; Schröder, B.; Maerker, M. How can statistical models help to determine driving factors of landslides? Ecol. Model. 2012, 239, 27–39. [Google Scholar] [CrossRef]
  65. Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 1–27. [Google Scholar] [CrossRef]
  66. Taha, M.M.; Elbarbary, S.M.; Naguib, D.M.; El-Shamy, I.Z. Flash flood hazard zonation based on basin morphometry using remote sensing and GIS techniques: A case study of Wadi Qena basin, Eastern Desert, Egypt. Remote Sens Appl Soc Environ. 2017, 8, 157–167. [Google Scholar] [CrossRef]
  67. Liang, L.; Lu, Y.L.; Yang, H. Toxicology of isoproturon to the food crop wheat as affected by salicylic acid. Environ. Sci. Pollut. Res. 2012, 19, 2044–2054. [Google Scholar] [CrossRef]
  68. Townsend, P.A.; Walsh, S.J. Modeling floodplain inundation using an integrated GIS with radar and optical remote sensing. Geomorphology 1998, 21, 295–312. [Google Scholar] [CrossRef]
  69. Farid, D.M.; Zhang, L.; Rahman, C.M.; Hossain, M.A.; Strachan, R. Hybrid decision tree and naïve Bayes classifiers for multi-class classification tasks. Expert Syst. Appl. 2014, 41, 1937–1946. [Google Scholar] [CrossRef]
  70. Pham, T.P.T.; Kaushik, R.; Parshetti, G.K.; Mahmood, R.; Balasubramanian, R. Food waste-to-energy conversion technologies: Current status and future directions. Waste Manag. 2015, 38, 399–408. [Google Scholar] [CrossRef] [PubMed]
  71. Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef] [Green Version]
  72. Wang, W.-C.; Ahmadi, M.H.; Xu, D.-M.; Chen, X.-Y. Improving Forecasting Accuracy of Annual Runoff Time Series Using ARIMA Based on EEMD Decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
  73. Hill, T.; Lewicki, P. Statistics: Methods and Applications: A Comprehensive Reference for Science, Industry and Data Mining; StatSoft, Inc.: Tulsa, OK, USA, 2006. [Google Scholar]
  74. Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
  75. Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
  76. Venables, W.N.; Smith, D.M.; R Development Core Team. An Introduction to r. A Programming Environment for Data Analysis and Graphics; R Development Core Team: Vienna, Austria, 2006. [Google Scholar]
  77. Ridgeway, G. Gbm: Generalized Boosted Regression Models, R package, version 2.1.1; R Foundation for Statistical Computing: Vienna, Austria; Available online: http://CRAN.R-project.org/package=gbm (accessed on 21 March 2017).
  78. Ozdemir, A. GIS-based groundwater spring potential mapping in the Sultan Mountains (Konya, Turkey) using frequency ratio, weights of evidence and logistic regression methods and their comparison. J. Hydrol. 2011, 411, 290–308. [Google Scholar] [CrossRef]
  79. Ozdemir, A. Using a binary logistic regression method and GIS for evaluating and mapping the groundwater spring potential in the Sultan Mountains (Aksehir, Turkey). J. Hydrol. 2011, 405, 123–136. [Google Scholar] [CrossRef]
  80. Ha, N.T.; Manley-Harris, M.; Pham, T.D.; Hawes, I. A Comparative Assessment of Ensemble-Based Machine Learning and Maximum Likelihood Methods for Mapping Seagrass Using Sentinel-2 Imagery in Tauranga Harbor, New Zealand. Remote Sens. 2020, 12, 355. [Google Scholar] [CrossRef] [Green Version]
  81. Naghibi, S.A.; Pourghasemi, H.R. A Comparative Assessment Between Three Machine Learning Models and Their Performance Comparison by Bivariate and Multivariate Statistical Methods in Groundwater Potential Mapping. Water Resour. Manag. 2015, 29, 5217–5236. [Google Scholar] [CrossRef]
  82. Naghibi, S.A.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Rezaei, A. Groundwater qanat potential mapping using frequency ratio and Shannon’s entropy models in the Moghan watershed, Iran. Earth Sci. Inform. 2015, 8, 171–186. [Google Scholar] [CrossRef]
  83. Rahmati, O.; Pourghasemi, H.R. Identification of critical flood prone areas in data-scarce and ungauged regions: A comparison of three data mining models. Water Resour. Manag. 2017, 31, 1473–1487. [Google Scholar] [CrossRef]
  84. Pourghasemi, H.R.; Xie, X.; Peng, J.B.; Dou, J.; Hong, H.; Bui, D.T.; Duan, Z.; Li, S.; Zhu, A.-X. GIS-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method. Catena 2018, 164, 135–149. [Google Scholar] [CrossRef]
  85. Nandi, A.; Shakoor, A. A GIS-based landslide susceptibility evaluation using bivariate and multivariate statistical analyses. Eng. Geol. 2009, 110, 11–20. [Google Scholar] [CrossRef]
  86. Hong, H.; Tsangaratos, P.; Ilia, I.; Liu, J.; Zhu, A.-X.; Chen, W. Application of fuzzy weight of evidence and data mining techniques in construction of flood susceptibility map of Poyang County, China. Sci. Total. Environ. 2018, 625, 575–588. [Google Scholar] [CrossRef]
  87. Shin, Y. Application of Boosting Regression Trees to Preliminary Cost Estimation in Building Construction Projects. Comput. Intell. Neurosci. 2015, 2015, 1–9. [Google Scholar] [CrossRef] [Green Version]
  88. Chauhan, S.; Sharma, M.; Arora, M.K. Landslide susceptibility zonation of the Chamoli region, Garhwal Himalayas, using logistic regression model. Landslides 2010, 7, 411–423. [Google Scholar] [CrossRef]
  89. Moisen, G.G.; Freeman, E.A.; Blackard, J.A.; Frescino, T.S.; Zimmermann, N.E.; Edwards, T.C. Predicting tree species presence and basal area in Utah: A comparison of stochastic gradient boosting, generalized additive models, and tree-based methods. Ecol. Model. 2006, 199, 176–187. [Google Scholar] [CrossRef]
  90. Osaragi, T. Classification Methods for Spatial Data Representation; Tokyo Institute of Technology: Tokyo, Japan, 2002. [Google Scholar]
  91. Green, J.I.; Nelson, E.J. Calculation of time of concentration for hydrologic design and analysis using geographic information system vector objects. J. Hydroinform. 2002, 4, 75–81. [Google Scholar] [CrossRef] [Green Version]
  92. Guisan, A.; Thuiller, W. Predicting species distribution: Offering more than simple habitat models. Ecol. Lett. 2005, 8, 993–1009. [Google Scholar] [CrossRef]
  93. Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J. Modeling spatial patterns of fire occurrence in Mediterranean Europe using Multiple Regression and Random Forest. For. Ecol. Manag. 2012, 275, 117–129. [Google Scholar] [CrossRef]
  94. Rahmati, O.; Falah, F.; Dayal, K.S.; Deo, R.; Mohammadi, F.; Biggs, T.; Moghaddam, D.D.; Naghibi, S.A.; Bui, D.T. Machine learning approaches for spatial modeling of agricultural droughts in the south-east region of Queensland Australia. Sci. Total Environ. 2019, 699, 134230. [Google Scholar] [CrossRef] [PubMed]
  95. Martins, S.; Bernardo, N.M.R.; Ogashawara, I.; Alcântara, E. Support Vector Machine algorithm optimal parameterization for change detection mapping in Funil Hydroelectric Reservoir (Rio de Janeiro State, Brazil). Model. Earth Syst. Environ. 2016, 2, 138. [Google Scholar] [CrossRef] [Green Version]
  96. Bathrellos, G.; Skilodimou, H.D.; Chousianitis, K.; Youssef, A.M.; Pradhan, B. Suitability estimation for urban development using multi-hazard assessment map. Sci. Total Environ. 2017, 575, 119–134. [Google Scholar] [CrossRef] [PubMed]
  97. Chen, W.; Hong, H.; Li, S.; Shahabi, H.; Wang, Y.; Wang, X.; Bin Ahmad, B. Flood susceptibility modelling using novel hybrid approach of reduced-error pruning trees with bagging and random subspace ensembles. J. Hydrol. 2019, 575, 864–873. [Google Scholar] [CrossRef]
Remotesensing 12 02695 g001 550
Figure 1. Raster map of perception showing the heaviest rainfall was 24 years ago in Khor Fakkan with 144 mm (5.66 inches) of accumulated rainfall (https://www.ncm.ae/). Photographs of flash flood damages during January 2020 in the RAK area, NUAE. Yellow points highlight flash flood locations across the study area.
Figure 1. Raster map of perception showing the heaviest rainfall was 24 years ago in Khor Fakkan with 144 mm (5.66 inches) of accumulated rainfall (https://www.ncm.ae/). Photographs of flash flood damages during January 2020 in the RAK area, NUAE. Yellow points highlight flash flood locations across the study area.
Remotesensing 12 02695 g001
Remotesensing 12 02695 g002 550
Figure 2. Elevation map generated from a DEM showing the location of the study area (white polygon), and main cities and towns of the study area (green stars).
Figure 2. Elevation map generated from a DEM showing the location of the study area (white polygon), and main cities and towns of the study area (green stars).
Remotesensing 12 02695 g002
Remotesensing 12 02695 g003 550
Figure 3. Monthly temperature and precipitation (a), number of days of rainfall (b), and daily precipitation (c) over the NUAE including the study area.
Figure 3. Monthly temperature and precipitation (a), number of days of rainfall (b), and daily precipitation (c) over the NUAE including the study area.
Remotesensing 12 02695 g003
Remotesensing 12 02695 g004 550
Figure 4. Flowchart of the methodology applied to the study area.
Figure 4. Flowchart of the methodology applied to the study area.
Remotesensing 12 02695 g004
Remotesensing 12 02695 g005 550
Figure 5. Maps of flash flood conditioning parameters used in flash flood susceptibility mapping: (a) altitude, (b) slope, (c) topographic minimum curvature, and (d) topographic relief.
Figure 5. Maps of flash flood conditioning parameters used in flash flood susceptibility mapping: (a) altitude, (b) slope, (c) topographic minimum curvature, and (d) topographic relief.
Remotesensing 12 02695 g005
Remotesensing 12 02695 g006 550
Figure 6. Maps of flash flood conditioning parameters used in flash flood susceptibility mapping: (a) lithology, (b) distance from streams, and (c) stream density.
Figure 6. Maps of flash flood conditioning parameters used in flash flood susceptibility mapping: (a) lithology, (b) distance from streams, and (c) stream density.
Remotesensing 12 02695 g006
Remotesensing 12 02695 g007 550
Figure 7. Diagrams represent Classification and Regression Trees (CART).
Figure 7. Diagrams represent Classification and Regression Trees (CART).
Remotesensing 12 02695 g007
Remotesensing 12 02695 g008 550
Figure 8. 3D Perspective view of Google Earth illustrates the geometry and new parameters used for estimating flash floods magnitudes (a), and the influence of repose angle, alluvial plain width, gradient and relief on flash flood occurrence (b).
Figure 8. 3D Perspective view of Google Earth illustrates the geometry and new parameters used for estimating flash floods magnitudes (a), and the influence of repose angle, alluvial plain width, gradient and relief on flash flood occurrence (b).
Remotesensing 12 02695 g008
Remotesensing 12 02695 g009 550
Figure 9. A comparison of precision (a), recall (b) and F1 score (c) for the FF susceptibility class using BRT, CART and NBT models.
Figure 9. A comparison of precision (a), recall (b) and F1 score (c) for the FF susceptibility class using BRT, CART and NBT models.
Remotesensing 12 02695 g009
Remotesensing 12 02695 g010 550
Figure 10. ROC curves for the FFS maps produced by BRT, CART and NBT.
Figure 10. ROC curves for the FFS maps produced by BRT, CART and NBT.
Remotesensing 12 02695 g010
Remotesensing 12 02695 g011 550
Figure 11. Flash flood susceptibility maps: (a) BRT, (b) CART, (c) NBT.
Figure 11. Flash flood susceptibility maps: (a) BRT, (b) CART, (c) NBT.
Remotesensing 12 02695 g011
Remotesensing 12 02695 g012 550
Figure 12. Maps of flash flood conditioning factors used for measuring FF magnitude: (a) basin area, (b) basin length, (c) relief.
Figure 12. Maps of flash flood conditioning factors used for measuring FF magnitude: (a) basin area, (b) basin length, (c) relief.
Remotesensing 12 02695 g012
Remotesensing 12 02695 g013 550
Figure 13. Maps of flash flood influencing conditioning factors used for measuring FF magnitude: (a) alluvial plain. width, (b) gradient, (c) mean slope.
Figure 13. Maps of flash flood influencing conditioning factors used for measuring FF magnitude: (a) alluvial plain. width, (b) gradient, (c) mean slope.
Remotesensing 12 02695 g013
Remotesensing 12 02695 g014 550
Figure 14. Maps of FF susceptibility obtained using a hybrid approach and new FFCPs (a), and its related infrastructures risk map (b).
Figure 14. Maps of FF susceptibility obtained using a hybrid approach and new FFCPs (a), and its related infrastructures risk map (b).
Remotesensing 12 02695 g014
Table
Table 1. Flash flood index parameters used for calculating flash flood magnitude for each zone (basin).
Table 1. Flash flood index parameters used for calculating flash flood magnitude for each zone (basin).
BasinLbBh (m)G°A (km2)AwMSFFM
RAK20001100331131343.393.24
Falaheyn15,00013005.21136927.630.57
Al Dhaid28,0006001.2815611314.780.16
Masafi500085010.2248.6439.033
Rul Dadnah-Dibba420095013.5406.63.535.312.96
Fujiarah-Kalba5000100012649332.522.71
Hatta-Houylate6000120012761.2232.161.11
Total 5893.4

Share and Cite

MDPI and ACS Style

Elmahdy, S.; Ali, T.; Mohamed, M. Flash Flood Susceptibility Modeling and Magnitude Index Using Machine Learning and Geohydrological Models: A Modified Hybrid Approach. Remote Sens. 2020, 12, 2695. https://doi.org/10.3390/rs12172695

AMA Style

Elmahdy S, Ali T, Mohamed M. Flash Flood Susceptibility Modeling and Magnitude Index Using Machine Learning and Geohydrological Models: A Modified Hybrid Approach. Remote Sensing. 2020; 12(17):2695. https://doi.org/10.3390/rs12172695

Chicago/Turabian Style

Elmahdy, Samy, Tarig Ali, and Mohamed Mohamed. 2020. "Flash Flood Susceptibility Modeling and Magnitude Index Using Machine Learning and Geohydrological Models: A Modified Hybrid Approach" Remote Sensing 12, no. 17: 2695. https://doi.org/10.3390/rs12172695

APA Style

Elmahdy, S., Ali, T., & Mohamed, M. (2020). Flash Flood Susceptibility Modeling and Magnitude Index Using Machine Learning and Geohydrological Models: A Modified Hybrid Approach. Remote Sensing, 12(17), 2695. https://doi.org/10.3390/rs12172695

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop