Soil Moisture Estimation for the Chinese Loess Plateau Using MODIS-derived ATI and TVDI
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Satellite Data and Image Pre-processing
2.3. In Situ Measured RSM Data
3. Methods
3.1. ATI and TVDI
3.1.1. Apparent Thermal Inertia (ATI)
3.1.2. Interpretation of the NDVI-LST Triangle Space
3.1.3. Temperature Vegetation Dryness Index (TVDI)
3.1.4. Applying Initial NDVI0 for Determination of TVDI
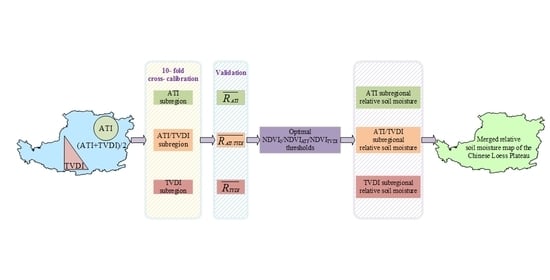
3.2. Establishment of the Retrieval Model
3.2.1. RSM Estimation for the ATI Subregion
3.2.2. RSM Estimation for the TVDI Subregion
3.2.3. RSM Estimation for the ATI/TVDI Subregion
3.2.4. Calibration and Validation
3.2.5. Identifying and Applying the Optimal NDVI Thresholds for Subregional RSM Retrieval
3.2.6. Combining Subregional RSM Maps to Generate overall RSM Maps
4. Results
4.1. Evaluation of the Calibration and Validation Results
4.1.1. Comparing Validation Results
4.1.2. The NDVIATI and NDVITVDI Thresholds for Generating Subregions
4.1.3. The Threshold NDVI0 for TVDI
4.2. Analysis of RSM Estimation Using an Optimal Model and Optimal NDVI Thresholds
4.2.1. Calibration and Validation Analysis of RSM Estimation
4.2.2. Estimated RSM Maps over the CLP
5. Discussion
5.1. Applicability of the ATI/TVDI Joint Model
5.2. Estimation of RSM in the CLP
5.3. Innovations and Limitations
6. Conclusions
- The whole study area was divided into three subregions by selected optimal NDVI thresholds and the overall RSM map was produced by combining subregional RSM maps over the CLP. This combination-based approach provides a new perspective for the mapping of RSM over large geographical areas.
- Spatiotemporal and comparative analysis indicated that the ATI/TVDI joint model had higher applicability (accounting for 36/38 periods) and accuracy than the ATI-based and TVDI-based models. The ATI-based model is only suitable for bare soil and sparsely vegetated areas while the TVDI-based model is more applicable to moderately or highly vegetated areas.
- The 10-fold cross-calibration method in the iteration procedure improves overall reliability and effectiveness in terms of identifying optimal NDVI thresholds.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ATI | Apparent thermal inertia |
| CLP | Chinese Loess Plateau |
| CMDC | China Meteorological Data Service Center |
| DOY | The day of the year |
| LST | Land surface temperature |
| MATI/TVDI | Mean of the value of ATI and TVDI |
| MAE | Mean absolute error |
| MODIS | Moderate Resolution Imaging Spectrometers |
| MRT | MODIS Reprojection Tool |
| NDVI | Normalized Difference Vegetation Index |
| NDVI0 | Initial NDVI for TVDI |
| NDVIATI | NDVI threshold for ATI subregion |
| NDVIATI/TVD | NDVI threshold for ATI/TVDI subregion |
| NDVITVDI | NDVI threshold for TVDI subregion |
| PDI | Perpendicular drought index |
| R2 | Coefficient of determination |
| R | Correlation coefficient |
| RMSE | Root Mean Square Error |
| RSM | Relative soil moisture |
| SM | Soil moisture |
| TVDI | Temperature Vegetation Dryness Index |
| UTC | The Coordinated Universal Time |
Appendix A
| Serial Number | Station | Latitude (°E) | Longitude (°N) | Serial Number | Station | Latitude (°E) | Longitude (°N) |
|---|---|---|---|---|---|---|---|
| 1 | 52,765 | 37.38 | 101.61 | 44 | 53,488 | 40.04 | 113.59 |
| 2 | 52,797 | 37.19 | 104.06 | 45 | 53,490 | 40.44 | 114.06 |
| 3 | 52,855 | 36.69 | 101.25 | 46 | 53,512 | 39.79 | 106.80 |
| 4 | 52,862 | 36.97 | 101.66 | 47 | 53,513 | 40.72 | 107.37 |
| 5 | 52,863 | 36.82 | 101.95 | 48 | 53,522 | 40.05 | 107.84 |
| 6 | 52,866 | 36.73 | 101.75 | 49 | 53,529 | 39.09 | 107.96 |
| 7 | 52,868 | 36.02 | 101.37 | 50 | 53,533 | 39.81 | 108.71 |
| 8 | 52,869 | 36.49 | 101.58 | 51 | 53,543 | 39.82 | 110.01 |
| 9 | 52,874 | 36.49 | 102.41 | 52 | 53,545 | 39.56 | 109.71 |
| 10 | 52,875 | 36.5 | 102.10 | 53 | 53,547 | 39.10 | 109.03 |
| 11 | 52,876 | 36.33 | 102.84 | 54 | 53,553 | 39.85 | 111.22 |
| 12 | 52,877 | 36.10 | 102.26 | 55 | 53,562 | 39.92 | 111.66 |
| 13 | 52,884 | 36.35 | 103.93 | 56 | 53,564 | 39.37 | 111.21 |
| 14 | 52,885 | 36.75 | 103.25 | 57 | 53,565 | 39.44 | 111.50 |
| 15 | 52,895 | 36.57 | 104.69 | 58 | 53,574 | 39.52 | 112.27 |
| 16 | 52,896 | 36.55 | 104.15 | 59 | 53,576 | 39.51 | 112.82 |
| 17 | 52,963 | 35.94 | 102.02 | 60 | 53,578 | 39.37 | 112.43 |
| 18 | 52,972 | 35.85 | 102.46 | 61 | 53,579 | 39.05 | 112.92 |
| 19 | 52,974 | 35.54 | 102.03 | 62 | 53,580 | 39.83 | 113.10 |
| 20 | 52,980 | 35.97 | 103.30 | 63 | 53,582 | 39.71 | 113.67 |
| 21 | 52,982 | 35.48 | 103.56 | 64 | 53,584 | 39.56 | 113.16 |
| 22 | 52,983 | 35.87 | 104.14 | 65 | 53,585 | 39.17 | 113.26 |
| 23 | 52,984 | 35.58 | 103.18 | 66 | 53,590 | 39.74 | 114.26 |
| 24 | 52,985 | 35.41 | 103.34 | 67 | 53,594 | 39.44 | 114.22 |
| 25 | 52,986 | 35.36 | 103.86 | 68 | 53,644 | 38.59 | 108.83 |
| 26 | 52,993 | 35.68 | 105.06 | 69 | 53,646 | 38.27 | 109.78 |
| 27 | 52,995 | 35.58 | 104.60 | 70 | 53,651 | 38.83 | 110.46 |
| 28 | 52,998 | 35.13 | 104.20 | 71 | 53,659 | 37.97 | 111.01 |
| 29 | 53,337 | 41.05 | 108.28 | 72 | 53,662 | 38.71 | 111.57 |
| 30 | 53,348 | 41.02 | 109.13 | 73 | 53,663 | 38.93 | 111.82 |
| 31 | 53,419 | 40.33 | 106.99 | 74 | 53,665 | 38.28 | 111.63 |
| 32 | 53,420 | 40.87 | 107.13 | 75 | 53,666 | 38.36 | 111.94 |
| 33 | 53,433 | 40.73 | 108.65 | 76 | 53,669 | 38.07 | 111.81 |
| 34 | 53,446 | 40.53 | 109.88 | 77 | 53,673 | 38.74 | 112.71 |
| 35 | 53,455 | 40.55 | 110.55 | 78 | 53,674 | 38.39 | 112.69 |
| 36 | 53,457 | 40.39 | 110.03 | 79 | 53,676 | 38.5 | 112.98 |
| 37 | 53,463 | 40.86 | 111.57 | 80 | 53,677 | 37.94 | 112.48 |
| 38 | 53,464 | 40.73 | 111.17 | 81 | 53,678 | 38.07 | 112.65 |
| 39 | 53,466 | 40.76 | 111.71 | 82 | 53,679 | 37.75 | 112.54 |
| 40 | 53,467 | 40.25 | 111.25 | 83 | 53,681 | 38.84 | 113.36 |
| 41 | 53,469 | 40.4 | 111.82 | 84 | 53,685 | 38.08 | 113.42 |
| 42 | 53,478 | 39.99 | 112.46 | 85 | 53,687 | 37.79 | 113.63 |
| 43 | 53,486 | 40.37 | 113.77 | 86 | 53,725 | 37.6 | 107.60 |
| 87 | 53,730 | 38.19 | 107.47 | 130 | 53,882 | 36.06 | 113.03 |
| 88 | 53,732 | 37.86 | 108.72 | 131 | 53,884 | 36.51 | 113.03 |
| 89 | 53,735 | 37.6 | 108.80 | 132 | 53,888 | 36.20 | 113.44 |
| 90 | 53,738 | 36.92 | 108.18 | 133 | 53,906 | 35.52 | 105.71 |
| 91 | 53,740 | 37.96 | 109.29 | 134 | 53,908 | 35.21 | 105.23 |
| 92 | 53,748 | 37.15 | 109.69 | 135 | 53,915 | 35.53 | 106.66 |
| 93 | 53,754 | 37.49 | 110.26 | 136 | 53,917 | 35.22 | 106.06 |
| 94 | 53,759 | 36.99 | 110.83 | 137 | 53,923 | 35.73 | 107.63 |
| 95 | 53,763 | 37.90 | 112.17 | 138 | 53,924 | 35.07 | 107.62 |
| 96 | 53,764 | 37.51 | 111.11 | 139 | 53,925 | 35.68 | 107.19 |
| 97 | 53,767 | 37.33 | 111.18 | 140 | 53,926 | 35.34 | 107.35 |
| 98 | 53,768 | 37.15 | 111.75 | 141 | 53,927 | 35.20 | 106.62 |
| 99 | 53,769 | 37.24 | 111.78 | 142 | 53,928 | 35.30 | 107.02 |
| 100 | 53,770 | 37.36 | 112.35 | 143 | 53,929 | 35.21 | 107.77 |
| 101 | 53,771 | 37.41 | 112.05 | 144 | 53,930 | 36.45 | 107.99 |
| 102 | 53,774 | 37.58 | 112.37 | 145 | 53,931 | 36.00 | 109.38 |
| 103 | 53,775 | 37.42 | 112.59 | 146 | 53,934 | 35.78 | 107.98 |
| 104 | 53,776 | 37.70 | 112.79 | 147 | 53,937 | 35.53 | 107.89 |
| 105 | 53,777 | 37.51 | 112.14 | 148 | 53,938 | 35.17 | 108.28 |
| 106 | 53,778 | 37.17 | 112.18 | 149 | 53,941 | 35.19 | 109.58 |
| 107 | 53,780 | 37.91 | 113.15 | 150 | 53,942 | 35.79 | 109.36 |
| 108 | 53,783 | 37.60 | 113.72 | 151 | 53,947 | 35.06 | 109.08 |
| 109 | 53,788 | 37.33 | 113.57 | 152 | 53,948 | 34.89 | 109.63 |
| 110 | 53,821 | 36.57 | 107.30 | 153 | 53,950 | 35.23 | 110.15 |
| 111 | 53,845 | 36.60 | 109.50 | 154 | 53,954 | 35.62 | 110.97 |
| 112 | 53,853 | 36.70 | 110.95 | 155 | 53,955 | 35.52 | 110.46 |
| 113 | 53,856 | 36.46 | 110.75 | 156 | 53,956 | 35.42 | 110.84 |
| 114 | 53,857 | 36.06 | 110.18 | 157 | 53,957 | 35.61 | 110.71 |
| 115 | 53,859 | 36.09 | 110.66 | 158 | 53,958 | 35.17 | 110.78 |
| 116 | 53,861 | 35.89 | 111.39 | 159 | 53,959 | 35.11 | 111.07 |
| 117 | 53,863 | 37.06 | 111.94 | 160 | 53,961 | 35.65 | 111.49 |
| 118 | 53,865 | 36.66 | 111.56 | 161 | 53,962 | 35.73 | 111.70 |
| 119 | 53,866 | 36.23 | 111.66 | 162 | 53,963 | 35.65 | 111.36 |
| 120 | 53,868 | 36.06 | 111.49 | 163 | 53,964 | 35.62 | 111.21 |
| 121 | 53,869 | 36.58 | 111.70 | 164 | 53,965 | 35.50 | 111.57 |
| 122 | 53,871 | 36.86 | 112.87 | 165 | 53,966 | 35.98 | 111.83 |
| 123 | 53,872 | 36.76 | 112.69 | 166 | 53,967 | 35.33 | 111.20 |
| 124 | 53,873 | 36.10 | 112.87 | 167 | 53,968 | 35.28 | 111.66 |
| 125 | 53,874 | 36.25 | 111.90 | 168 | 53,970 | 35.69 | 112.19 |
| 126 | 53,877 | 36.16 | 112.25 | 169 | 53,973 | 35.78 | 112.94 |
| 127 | 53,878 | 36.51 | 113.36 | 170 | 53,975 | 35.49 | 112.41 |
| 128 | 53,879 | 36.32 | 112.89 | 171 | 53,976 | 35.50 | 112.86 |
| 129 | 53,880 | 36.34 | 113.23 | 172 | 53,978 | 35.09 | 112.63 |
| 173 | 56,092 | 34.99 | 104.65 | 194 | 57,042 | 34.78 | 109.19 |
| 174 | 57,001 | 34.75 | 105.33 | 195 | 57,043 | 34.80 | 109.97 |
| 175 | 57,003 | 34.89 | 106.84 | 196 | 57,044 | 34.40 | 109.23 |
| 176 | 57,004 | 34.73 | 104.88 | 197 | 57,045 | 34.40 | 109.49 |
| 177 | 57,014 | 34.56 | 105.87 | 198 | 57,047 | 34.16 | 109.32 |
| 178 | 57,020 | 34.36 | 107.39 | 199 | 57,048 | 34.40 | 108.72 |
| 179 | 57,022 | 34.68 | 107.80 | 200 | 57,051 | 34.79 | 111.19 |
| 180 | 57,024 | 34.44 | 107.65 | 201 | 57,052 | 34.88 | 110.45 |
| 181 | 57,025 | 34.51 | 107.38 | 202 | 57,053 | 34.70 | 110.71 |
| 182 | 57,026 | 34.37 | 107.88 | 203 | 57,055 | 34.59 | 110.13 |
| 183 | 57,027 | 34.30 | 107.73 | 204 | 57,060 | 35.16 | 111.22 |
| 184 | 57,029 | 34.49 | 108.45 | 205 | 57,061 | 34.84 | 111.20 |
| 185 | 57,030 | 34.69 | 108.14 | 206 | 57,066 | 34.40 | 111.67 |
| 186 | 57,031 | 34.83 | 108.55 | 207 | 57,071 | 34.80 | 112.47 |
| 187 | 57,032 | 34.14 | 108.21 | 208 | 57,074 | 34.42 | 112.40 |
| 188 | 57,033 | 34.56 | 108.53 | 209 | 57,076 | 34.74 | 112.79 |
| 189 | 57,034 | 34.31 | 108.24 | 210 | 57,080 | 34.74 | 112.97 |
| 190 | 57,035 | 34.54 | 108.25 | 211 | 57,123 | 34.29 | 108.07 |
| 191 | 57,037 | 34.92 | 108.98 | 212 | 57,131 | 34.45 | 108.97 |
| 192 | 57,038 | 34.28 | 108.48 | 213 | 57,132 | 34.14 | 108.58 |
| 193 | 57,041 | 34.63 | 108.93 |
| Abbreviation | Formula |
|---|---|
| R2 | |
| R | |
| RMSE | |
| MAE | |
| STD |
| DOY | Calibration | Validation | ||||
|---|---|---|---|---|---|---|
| Model | Fitting Equation | R2 | R2 | RMSE | MAE | |
| 17 | ATI/TVDI | y = 70.61x − 6.39 | 0.36 *** | 1.00 | 0.91 | 0.90 |
| 25 | ATI | y = −239.74x + 19.98 | 0.28 * | 1.00 | 1.89 | 1.36 |
| 41 | ATI | y = 259.54x + 2.732 | 0.23 ** | 1.00 | 0.99 | 0.74 |
| 49 | ATI/TVDI | y = 32.06x + 1.64 | 0.20 ** | 0.57 | 3.50 | 3.39 |
| 57 | ATI/TVDI | y = 56.46x − 2.16 | 0.19 ** | 0.97 | 1.00 | 0.97 |
| 81 | ATI/TVDI | y = 35.11x + 6.41 | 0.38 ** | 1.00 | 1.95 | 1.82 |
| 89 | ATI/TVDI | y = 30.24x + 7.22 | 0.12 ** | 0.43 | 2.96 | 2.49 |
| 97 | ATI/TVDI | y = 20.34x + 8.26 | 0.30 *** | 0.48 | 3.57 | 3.56 |
| 105 | ATI/TVDI | y = 36.52x + 8.20 | 0.10 ** | 0.68 | 1.37 | 1.18 |
| 113 | ATI/TVDI | y = 75.22x + 3.21 | 0.33 ** | 0.67 | 2.11 | 1.38 |
| 121 | ATI/TVDI | y = 71.01x − 0.785 | 0.25 ** | 0.55 | 2.09 | 1.93 |
| 129 | ATI/TVDI | y = 49.47x − 2.46 | 0.43 ** | 1.00 | 3.10 | 2.44 |
| 137 | ATI/TVDI | y = −75.55x + 22.47 | 0.66 *** | 0.72 | 3.63 | 2.71 |
| 145 | ATI/TVDI | y = −92.69x + 27.00 | 0.30 ** | 0.93 | 2.81 | 2.48 |
| 153 | ATI | y = −303.76x + 25.47 | 0.12 *** | 0.86 | 2.21 | 2.08 |
| ATI/TVDI | y = 70.05x + 2.73 | 0.22 ** | 1.00 | 1.54 | 1.30 | |
| TVDI | y = −26.78x + 21.12 | 0.24 ** | 0.48 | 1.57 | 1.21 | |
| 161 | ATI/TVDI | y = −237.90x + 24.39 | 0.28 *** | 0.73 | 4.82 | 4.06 |
| ATI | y = 37.57x + 3.66 | 0.19 * | 0.92 | 5.25 | 3.82 | |
| 169 | ATI/TVDI | y = 53.34x + 5.72 | 0.44 ** | 1.00 | 0.30 | 0.27 |
| 177 | ATI/TVDI | y = 57.34x + 1.22 | 0.29 ** | 0.48 | 2.12 | 1.60 |
| 185 | ATI/TVDI | y = 67.79x − 1.69 | 0.42 *** | 0.99 | 3.47 | 2.88 |
| 193 | ATI/TVDI | y = 38.35x + 1.11 | 0.11 * | 0.33 | 5.78 | 4.75 |
| 209 | ATI/TVDI | y = 92.55x − 8.24 | 0.40 *** | 0.99 | 2.48 | 1.95 |
| 217 | ATI/TVDI | y = 88.95x − 1.72 | 0.37 *** | 0.63 | 3.78 | 3.75 |
| 233 | ATI/TVDI | y = 40.50x + 4.53 | 0.17 * | 0.60 | 3.39 | 2.61 |
| 249 | ATI/TVDI | y = −235.66x + 27.89 | 0.32 *** | 0.39 | 2.77 | 2.36 |
| ATI | y = 54.38x + 5.53 | 0.23 ** | 0.97 | 1.89 | 1.56 | |
| 257 | ATI/TVDI | y = −159.38x + 24.87 | 0.15 *** | 0.46 | 4.44 | 3.61 |
| ATI | y = 64.42x + 1.02 | 0.39 *** | 0.40 | 7.49 | 6.40 | |
| 265 | ATI/TVDI | y = 58.62x + 5.45 | 0.42 *** | 0.58 | 2.97 | 2.73 |
| 273 | ATI/TVDI | y = −38.13x + 22.98 | 0.23 *** | 0.90 | 2.58 | 2.37 |
| ATI | y = 63.82x + 2.86 | 0.27 ** | 0.28 | 6.75 | 5.73 | |
| 281 | ATI/TVDI | y = −57.46x + 32.93 | 0.46 *** | 0.66 | 1.85 | 1.81 |
| 289 | ATI/TVDI | y = −35.11x + 25.12 | 0.15 ** | 0.78 | 3.85 | 3.47 |
| 297 | ATI/TVDI | y = 85.81x-8.40 | 0.47 *** | 0.98 | 0.89 | 0.81 |
| 305 | ATI/TVDI | y = 53.85x + 4.76 | 0.23 *** | 0.70 | 2.79 | 2.40 |
| 313 | ATI/TVDI | y = 21.85x + 7.78 | 0.15 * | 0.84 | 2.68 | 2.19 |
| 321 | ATI/TVDI | y = 55.92x − 1.92 | 0.26 *** | 0.97 | 1.12 | 1.03 |
| 329 | ATI/TVDI | y = 70.01x − 7.01 | 0.48 *** | 1.00 | 1.88 | 1.31 |
| 337 | ATI/TVDI | y = 57.54x − 4.17 | 0.47 *** | 0.86 | 1.94 | 1.55 |
| 345 | ATI/TVDI | y = 56.01x − 5.73 | 0.32 *** | 0.56 | 2.36 | 1.87 |
| 353 | ATI/TVDI | y = 49.16x − 4.13 | 0.43 *** | 0.90 | 2.05 | 2.04 |
| ATI/TVDI | y = 62.46x − 5.29 | 0.41 *** | 0.81 | 1.89 | 1.80 | |
| 361 | TVDI | y = 22.66x − 1.25 | 0.14 *** | 0.53 | 2.91 | 2.43 |
| ATI/TVDI | y = 91.96x − 14.32 | 0.36 *** | 0.95 | 2.41 | 2.02 | |
| Month/Season | DOY | Station | Observed RSM (%) | Combined Model | ATI-Based Model | TVDI-Based Model | |||
|---|---|---|---|---|---|---|---|---|---|
| Estimated RSM (%) | R-Value in Calibration | Estimated RSM (%) | R-Value in Calibration | Estimated RSM (%) | R-Value in Calibration | ||||
| Jan/Winter | 17 | 53,735 | 0.80 | 5.99 | 0.60 | 9.51 | 0.37 | 6.96 | 0.45 |
| 53,931 | 5.85 | 6.89 | 10.99 | 7.90 | |||||
| 57,055 | 13.43 | 12.36 | 10.32 | 11.49 | |||||
| 53,978 | 16.15 | 11.16 | 10.76 | 10.77 | |||||
| 53,934 | 3.16 | 3.60 | 11.20 | 5.71 | |||||
| Apr/Spring | 97 | 53,543 | 7.22 | 10.58 | 0.55 | 15.03 | 0.12 | 14.54 | 0.11 |
| 53,651 | 12.82 | 14.65 | 14.66 | 15.15 | |||||
| 53,681 | 18.08 | 17.45 | 14.29 | 15.79 | |||||
| 53,754 | 12.18 | 12.18 | 14.75 | 15.22 | |||||
| 53,959 | 10.68 | 12.00 | 15.10 | 15.20 | |||||
| May/Spring | 137 | 53,433 | 5.90 | 6.77 | 0.81 | 10.83 | 0.09 | 10.62 | 0.08 |
| 53,469 | 7.50 | 7.00 | 10.93 | 10.63 | |||||
| 53,732 | 5.62 | 4.01 | 11.22 | 10.33 | |||||
| 53,863 | 8.21 | 8.11 | 11.18 | 10.70 | |||||
| 53,678 | 8.29 | 6.85 | 11.17 | 10.59 | |||||
| Jun/Summer | 161 | 53,915 | 11.72 | 13.11 | 0.49/0.53/0.44 | 14.17 | 0.43 | 14.10 | 0.33 |
| 53,585 | 8.74 | 11.36 | 13.17 | 11.75 | |||||
| 53,659 | 10.35 | 11.72 | 13.67 | 12.93 | |||||
| 52,765 | 29.38 | 15.42 | 15.02 | 7.30 | |||||
| 57,080 | 18.23 | 17.78 | 15.88 | 14.91 | |||||
| Jul/Summer | 209 | 53,433 | 3.67 | 6.19 | 0.63 | 14.51 | 0.09 | 12.40 | 0.25 |
| 52,765 | 33.95 | 23.62 | 13.85 | 17.46 | |||||
| 53,754 | 16.21 | 16.23 | 14.92 | 14.84 | |||||
| 57,131 | 13.50 | 13.75 | 14.37 | 14.51 | |||||
| 57,071 | 13.07 | 13.69 | 14.22 | 14.58 | |||||
| Oct/Autumn | 297 | 53,748 | 11.77 | 12.98 | 0.69 | 17.20 | 0.28 | 16.64 | 0.27 |
| 57,052 | 14.20 | 14.11 | 18.03 | 17.21 | |||||
| 53,872 | 21.58 | 20.95 | 13.83 | 18.73 | |||||
| 53,676 | 11.78 | 12.25 | 16.72 | 16.28 | |||||
| 53,776 | 13.82 | 15.21 | 16.53 | 17.28 | |||||
| Nov/Autumn | 329 | 53,512 | 4.00 | 7.22 | 0.69 | 12.59 | 0.32 | 8.10 | 0.59 |
| 53,553 | 3.53 | 5.70 | 11.57 | 6.00 | |||||
| 53,585 | 2.99 | 6.52 | 12.44 | 7.37 | |||||
| 53,780 | 9.14 | 10.66 | 12.18 | 10.83 | |||||
| 53,868 | 16.50 | 15.26 | 11.95 | 14.71 | |||||
| Dec/Winter | 353 | 53,478 | 2.72 | 0.99 | 0.66/0.64 | 8.82 | 0.30 | 0.59 | 0.49 |
| 53,585 | 2.09 | 6.35 | 9.52 | 7.99 | |||||
| 53,651 | 3.40 | 7.47 | 9.09 | 8.67 | |||||
| 57,053 | 14.30 | 13.29 | 9.69 | 12.15 | |||||
| 57,071 | 16.94 | 14.41 | 9.83 | 13.13 | |||||
References
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Njoku, E.G.; Kong, J.-A. Theory for passive microwave remote sensing of near-surface soil moisture. J. Geophys. Res. Space Phys. 1977, 82, 3108–3118. [Google Scholar] [CrossRef]
- Colliander, A.; Chan, S.; Kim, S.-B.; Das, N.; Yueh, S.; Cosh, M.H.; Bindlish, R.; Jackson, T.; Njoku, E. Long term analysis of PALS soil moisture campaign measurements for global soil moisture algorithm development. Remote Sens. Environ. 2012, 121, 309–322. [Google Scholar] [CrossRef]
- Ines, A.V.; Das, N.N.; Hansen, J.W.; Njoku, E.G. Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction. Remote Sens. Environ. 2013, 138, 149–164. [Google Scholar] [CrossRef] [Green Version]
- Rahimzadeh-Bajgiran, P.; Berg, A.A.; Champagne, C.; Omasa, K. Estimation of soil moisture using optical/thermal infrared remote sensing in the Canadian Prairies. ISPRS J. Photogramm. Remote Sens. 2013, 83, 94–103. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, G. Estimation of Soil Moisture from Optical and Thermal Remote Sensing: A Review. Sensors 2016, 16, 1308. [Google Scholar] [CrossRef] [Green Version]
- Carlson, T.N.; Petropoulos, G.P. A new method for estimating of evapotranspiration and surface soil moisture from optical and thermal infrared measurements: The simplified triangle. Int. J. Remote Sens. 2019, 40, 7716–7729. [Google Scholar] [CrossRef]
- Holidi, H.; Armanto, M.E.; Damiri, N.; Putranto, D.D.A. Characteristics of Selected Peatland uses and Soil Moisture Based on TVDI. J. Ecol. Eng. 2019, 20, 194–200. [Google Scholar] [CrossRef]
- Rahimzadeh-Bajgiran, P.; Omasa, K.; Shimizu, Y. Comparative evaluation of the Vegetation Dryness Index (VDI), the Temperature Vegetation Dryness Index (TVDI) and the improved TVDI (iTVDI) for water stress detection in semi-arid regions of Iran. ISPRS J. Photogramm. Remote Sens. 2012, 68, 1–12. [Google Scholar] [CrossRef]
- Wang, H.; He, N.; Zhao, R.; Ma, X. Soil water content monitoring using joint application of PDI and TVDI drought indices. Remote Sens. Lett. 2020, 11, 455–464. [Google Scholar] [CrossRef]
- Price, J.C. Thermal inertia mapping: A new view of the Earth. J. Geophys. Res. Space Phys. 1977, 82, 2582–2590. [Google Scholar] [CrossRef]
- Wang, Y.; Bian, Z.; Lei, S.; Zhang, Y. Investigating spatial and temporal variations of soil moisture content in an arid mining area using an improved thermal inertia model. J. Arid. Land 2017, 9, 712–726. [Google Scholar] [CrossRef]
- Minacapilli, M.; Cammalleri, C.; Ciraolo, G.; D’Asaro, F.; Iovino, M.; Maltese, A. Thermal Inertia Modeling for Soil Surface Water Content Estimation: A Laboratory Experiment. Soil Sci. Soc. Am. J. 2012, 76, 92–100. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite remote sensing applications for surface soil moisture monitoring: A review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Lu, S.; Ju, Z.; Ren, T.; Horton, R. A general approach to estimate soil water content from thermal inertia. Agric. For. Meteorol. 2009, 149, 1693–1698. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Veroustraete, F.; Van Der Sande, C.J.; Grootaers, I.; Feyen, J. Soil moisture retrieval using thermal inertia, determined with visible and thermal spaceborne data, validated for European forests. Remote Sens. Environ. 2006, 101, 299–314. [Google Scholar] [CrossRef]
- Lu, X.J.; Zhou, B.; Yan, H.B.; Luo, L.; Huang, Y.H.; Wu, C.L. Remote Sensing Retrieval of Soil Moisture in Guangxi Based on Ati and Tvdi Models. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 42, 895–902. [Google Scholar] [CrossRef] [Green Version]
- Hsu, W.-L.; Chang, K.-T. Cross-estimation of Soil Moisture Using Thermal Infrared Images with Different Resolutions. Sensors Mater. 2019, 31, 387. [Google Scholar] [CrossRef]
- Kang, J.; Jin, R.; Li, X.; Ma, C.; Qin, J.; Zhang, Y. High spatio-temporal resolution mapping of soil moisture by integrating wireless sensor network observations and MODIS apparent thermal inertia in the Babao River Basin, China. Remote Sens. Environ. 2017, 191, 232–245. [Google Scholar] [CrossRef] [Green Version]
- Fan, L.; Al-Yaari, A.; Frappart, F.; Swenson, J.J.; Xiao, Q.; Wen, J.; Jin, R.; Kang, J.; Li, X.; Fernandez-Moran, R.; et al. Mapping Soil Moisture at a High Resolution over Mountainous Regions by Integrating In Situ Measurements, Topography Data, and MODIS Land Surface Temperatures. Remote Sens. 2019, 11, 656. [Google Scholar] [CrossRef] [Green Version]
- Lei, S.-G.; Bian, Z.-F.; Daniels, J.L.; Liu, D.-L. Improved spatial resolution in soil moisture retrieval at arid mining area using apparent thermal inertia. Trans. Nonferrous Met. Soc. China 2014, 24, 1866–1873. [Google Scholar] [CrossRef]
- Taktikou, E.; Papaioannou, G.; Bourazanis, G.; Kerkides, P. Soil moisture assessment from MODIS data. Desalin. Water Treat. 2017, 99, 59–71. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, J.; Cheng, F.; Chen, Y. Soil Moisture by Remote Sensing Retrieval in the Tropic of Cancer of Yunnan Province. Pol. J. Environ. Stud. 2020, 29, 1981–1993. [Google Scholar] [CrossRef]
- Markovic, S.B.; Stevens, T.; Mason, J.A.; Vandenberghe, J.; Yang, S.; Veres, D.; Újvári, G.; Timar-Gabor, A.; Zeeden, C.; Guo, Z.; et al. Loess correlations—Between myth and reality. Palaeogeogr. Palaeoclim. Palaeoecol. 2018, 509, 4–23. [Google Scholar] [CrossRef]
- Veroustraete, F.; Li, Q.; Verstraeten, W.W.; Chen, X.; Bao, A.; Dong, Q.; Liu, T.; Willems, P. Soil moisture content retrieval based on apparent thermal inertia for Xinjiang province in China. Int. J. Remote Sens. 2011, 33, 3870–3885. [Google Scholar] [CrossRef]
- Scheidt, S.; Ramsey, M.; Lancaster, N. Determining soil moisture and sediment availability at White Sands Dune Field, New Mexico, from apparent thermal inertia data. J. Geophys. Res. Space Phys. 2010, 115, 115. [Google Scholar] [CrossRef]
- Van Doninck, J.; Peters, J.; De Baets, B.; De Clercq, E.M.; Ducheyne, E.; Verhoest, N.E.C. The potential of multitemporal Aqua and Terra MODIS apparent thermal inertia as a soil moisture indicator. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 934–941. [Google Scholar] [CrossRef]
- Moran, M.; Clarke, T.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Masjedi, A.; Dehnavi, S. Temperature-Vegetation-soil Moisture Dryness Index (TVMDI). Remote Sens. Environ. 2017, 197, 1–14. [Google Scholar] [CrossRef]
- Holzman, M.E.; Rivas, R.E.; Bayala, M. Subsurface Soil Moisture Estimation by VI–LST Method. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1951–1955. [Google Scholar] [CrossRef]
- Son, N.-T.; Chen, C.-F.; Chen, C.-R.; Masferrer, M.-G.-M.; Recinos, L.-E.-M.; Castellón, A. Multitemporal Landsat-MODIS fusion for cropland drought monitoring in El Salvador. Geocarto Int. 2018, 34, 1363–1383. [Google Scholar] [CrossRef]
- Moon, H.; Choi, M. Dryness Indices Based on Remotely Sensed Vegetation and Land Surface Temperature for Evaluating the Soil Moisture Status in Cropland-Forest-Dominant Watersheds. Terr. Atmos. Ocean. Sci. 2015, 26, 599. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Yao, Z.; Wang, R. Evaluating the surface temperature and vegetation index (Ts/VI) method for estimating surface soil moisture in heterogeneous regions. Hydrol. Res. 2017, 49, 689–699. [Google Scholar] [CrossRef]
- Shi, S.; Yao, F.; Zhang, J.; Yang, S. Evaluation of Temperature Vegetation Dryness Index on Drought Monitoring Over Eurasia. IEEE Access 2020, 8, 30050–30059. [Google Scholar] [CrossRef]
- Zhao, C.; Jia, X.; Zhu, Y.; Shao, M. Long-term temporal variations of soil water content under different vegetation types in the Loess Plateau, China. Catena 2017, 158, 55–62. [Google Scholar] [CrossRef]
- Xiao, L.; Xue, S.; Liu, G.; Zhang, C. Soil Moisture Variability under Different Land Uses in the Zhifanggou Catchment of the Loess Plateau, China. Arid. Land Res. Manag. 2014, 28, 274–290. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Jiang, H.; Mao, L.; Yu, Z. Estimating soil moisture using Temperature–Vegetation Dryness Index (TVDI) in the Huang-huai-hai (HHH) plain. Int. J. Remote Sens. 2011, 32, 1165–1177. [Google Scholar] [CrossRef]
- Song, Y.; Fang, S.; Yang, Z.; Shen, S. Drought indices based on MODIS data compared over a maize-growing season in Songliao Plain, China. J. Appl. Remote Sens. 2018, 12, 046003. [Google Scholar] [CrossRef]
- Lanjie, D.; Wei, W.; Hexi, C.; Zining, N. Remote sensing inversion of soil moisture in Hebei Plain based on ATI and TVDI models. Chin. J. Eco Agric. 2014, 22, 737–743. [Google Scholar]
- Patel, N.; Anapashsha, R.; Kumar, S.; Saha, S.K.; Dadhwal, V.K. Assessing potential of MODIS derived temperature/vegetation condition index (TVDI) to infer soil moisture status. Int. J. Remote Sens. 2008, 30, 23–39. [Google Scholar] [CrossRef]
- Sun, L.; Sun, R.; Li, X.; Liang, S.; Zhang, R. Monitoring surface soil moisture status based on remotely sensed surface temperature and vegetation index information. Agric. For. Meteorol. 2012, 166, 175–187. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, Proximal, and Satellite Remote Sensing of Soil Moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Yue, H. The Temperature Vegetation Dryness Index (TVDI) Based on Bi-Parabolic NDVI-Ts Space and Gradient-Based Structural Similarity (GSSIM) for Long-Term Drought Assessment across Shaanxi Province, China (2000–2016). Remote Sens. 2018, 10, 959. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.L.; Qin, Q.M.; Sun, Y.J.; Zheng, X.P.; Wu, L.; Wang, N. Improvement of TVDI for soil moisture estimation. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec, QC, Canada, 13–18 July 2014; pp. 3255–3258. [Google Scholar] [CrossRef]
- Shen, R.; Yu, P.; Yan, J.; Wang, Y. Retrieving Soil Moisture by TVDI Based on Different Vegetation Index: A Case Study of Shanxi Province. In Proceedings of the 2012 International Conference on Computer Science and Electronics Engineering, Hangzhou, China, 23–25 March 2012; pp. 418–422. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, L.-W.; Shi, J.-J.; Huang, J. Soil Moisture Monitoring Based on Land Surface Temperature-Vegetation Index Space Derived from MODIS Data. Pedosphere 2014, 24, 450–460. [Google Scholar] [CrossRef]
- Wong, T.-T.; Yang, N.-Y. Dependency Analysis of Accuracy Estimates in k-Fold Cross Validation. IEEE Trans. Knowl. Data Eng. 2017, 29, 2417–2427. [Google Scholar] [CrossRef]
- Jung, Y. Multiple predictingK-fold cross-validation for model selection. J. Nonparametr. Stat. 2017, 30, 197–215. [Google Scholar] [CrossRef]
- Bengio, Y.; Grandvalet, Y. No unbiased estimator of the variance of K-fold cross-validation. J. Mach. Learn. Res. 2004, 5, 1089–1105. [Google Scholar]
- Filion, R.; Bernier, M.; Paniconi, C.; Chokmani, K.; Melis, M.; Soddu, A.; Talazac, M.; LaFortune, F.-X. Remote sensing for mapping soil moisture and drainage potential in semi-arid regions: Applications to the Campidano plain of Sardinia, Italy. Sci. Total Environ. 2016, 543, 862–876. [Google Scholar] [CrossRef]
- Lievens, H.; Verhoest, N.E.C. Spatial and temporal soil moisture estimation from RADARSAT-2 imagery over Flevoland, The Netherlands. J. Hydrol. 2012, 456, 44–56. [Google Scholar] [CrossRef]
- Baldwin, D.; Manfreda, S.; Keller, K.; Smithwick, E. Predicting root zone soil moisture with soil properties and satellite near-surface moisture data across the conterminous United States. J. Hydrol. 2017, 546, 393–404. [Google Scholar] [CrossRef]
- Weiss, S.M.; Kulikowski, C.A. Computer Systems That Learn: Classification and Prediction Methods from Statistics, Neural Nets, Machine Learning and Expert Systems; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1991. [Google Scholar]
- Su, C.; Fu, B. Evolution of ecosystem services in the Chinese Loess Plateau under climatic and land use changes. Glob. Planet. Chang. 2013, 101, 119–128. [Google Scholar] [CrossRef]
- Level-1 and Atmosphere Archive and Distribution System (LAADS) Distributed Archive Center (DAAC). Available online: https://ladsweb.modaps.eosdis.nasa.gov/ (accessed on 21 February 2019).
- Vermote Eric, F. MODIS Surface Reflectance User’s Guide Collection 6. Available online: http://modis-sr.ltdri.org/guide/MOD09_UserGuide_v1.4.pdf (accessed on 15 November 2018).
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- China Meteorological Data Service Center. Available online: http://data.cma.cn/en (accessed on 11 January 2019).
- González, R.; López, A.; Iagnemma, K. Thermal vision, moisture content, and vegetation in the context of off-road mobile robots. J. Terramechanics 2017, 70, 35–48. [Google Scholar] [CrossRef]
- Matsushima, D.; Asanuma, J.; Kaihotsu, I. Thermal Inertia Approach Using a Heat Budget Model to Estimate the Spatial Distribution of Surface Soil Moisture over a Semiarid Grassland in Central Mongolia. J. Hydrometeorol. 2018, 19, 245–265. [Google Scholar] [CrossRef]
- Claps, P.; LaGuardia, G. Assessing spatial variability of soil water content through thermal inertia and NDVI. Remote Sens. 2004, 5232, 378–388. [Google Scholar] [CrossRef]
- Price, J.C. On the analysis of thermal infrared imagery: The limited utility of apparent thermal inertia. Remote Sens. Environ. 1985, 18, 59–73. [Google Scholar] [CrossRef]
- Liang, S.; Shuey, C.J.; Russ, A.L.; Fang, H.; Chen, M.; Walthall, C.L.; Daughtry, C.S.T.; Hunt, R., Jr. Narrowband to broadband conversions of land surface albedo: II. Validation. Remote Sens. Environ. 2003, 84, 25–41. [Google Scholar] [CrossRef]
- Goetz, S.J. Multi-sensor analysis of NDVI, surface temperature and biophysical variables at a mixed grassland site. Int. J. Remote Sens. 1997, 18, 71–94. [Google Scholar] [CrossRef]
- Tagesson, T.; Horion, S.; Nieto, H.; Fornies, V.Z.; Gonzalez, G.M.; Bulgin, C.E.; Ghent, D.; Fensholt, R. Disaggregation of SMOS soil moisture over West Africa using the Temperature and Vegetation Dryness Index based on SEVIRI land surface parameters. Remote Sens. Environ. 2018, 206, 424–441. [Google Scholar] [CrossRef] [Green Version]
- Gillies, R.R.; Kustas, W.P.; Humes, K.S. A verification of the ’triangle’ method for obtaining surface soil water content and energy fluxes from remote measurements of the Normalized Difference Vegetation Index (NDVI) and surface e. Int. J. Remote Sens. 1997, 18, 3145–3166. [Google Scholar] [CrossRef]
- Cho, J.; Lee, Y.-W.; Lee, H.-S. Assessment of the relationship between thermal-infrared-based temperature−vegetation dryness index and microwave satellite-derived soil moisture. Remote Sens. Lett. 2014, 5, 627–636. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Chen, X.; Chen, J. Identification of Concealed Faults in a Grassland Area in Inner Mongolia, China, Using the Temperature Vegetation Dryness Index. J. Earth Sci. 2018, 30, 853–860. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Zhou, Q.; Wu, J.; Peng, J.; Chang, H. Spatiotemporal variability of land surface moisture based on vegetation and temperature characteristics in Northern Shaanxi Loess Plateau, China. J. Arid. Environ. 2008, 72, 974–985. [Google Scholar] [CrossRef]
- Younis, S.M.Z.; Iqbal, J. Estimation of soil moisture using multispectral and FTIR techniques. Egypt. J. Remote Sens. Space Sci. 2015, 18, 151–161. [Google Scholar] [CrossRef] [Green Version]
- Son, N.; Chen, C.; Chang, L.; Minh, V.; Chen, C. Monitoring agricultural drought in the Lower Mekong Basin using MODIS NDVI and land surface temperature data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 417–427. [Google Scholar] [CrossRef]
- Du, L.; Song, N.; Liu, K.; Hou, J.; Hu, Y.; Zhu, Y.; Wang, X.; Wang, L.; Guo, Y. Comparison of Two Simulation Methods of the Temperature Vegetation Dryness Index (TVDI) for Drought Monitoring in Semi-Arid Regions of China. Remote Sens. 2017, 9, 177. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Jia, S.; Lv, A. A time domain solution of the Modified Temperature Vegetation Dryness Index (MTVDI) for continuous soil moisture monitoring. Remote Sens. Environ. 2017, 200, 1–17. [Google Scholar] [CrossRef]
- Amiri, M.; Jafari, R.; Tarkesh, M.; Modarres, R. Spatiotemporal variability of soil moisture in arid vegetation communities using MODIS vegetation and dryness indices. Arid. Land Res. Manag. 2019, 34, 1–25. [Google Scholar] [CrossRef]
- Chen, Q.; Miao, F.; Xu, Z.-X.; Wang, H.; Yang, L.; Tang, Z. Downscaling of Remote Sensing Soil Moisture Products Based on TVDI in Complex Terrain Areas. In Proceedings of the 2019 International Conference on Meteorology Observations (ICMO), Chengdu, China, 28–31 December 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Y. Research on the method for retrieving soil moisture using thermal inertia model. Sci. China Ser. D Earth Sci. 2006, 49, 539–545. [Google Scholar] [CrossRef]
- Zhao, J.-P.; Zhang, X.; Bao, H.-Y.; Tong, Q.-X.; Wang, X.-Y.; Liao, C.-H. Monitoring land surface soil moisture: Co-inversion of visible, infrared and passive microwave sensing data. J. Infrared Millim. Waves 2012, 31, 137–142. [Google Scholar] [CrossRef]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B Stat. Methodol. 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Seni, G.; Elder, J.F. Ensemble Methods in Data Mining: Improving Accuracy through Combining Predictions. Synth. Lect. Data Min. Knowl. Discov. 2010, 2, 1–126. [Google Scholar] [CrossRef]
- Li, L.; Bakelants, L.; Solana, C.; Canters, F.; Kervyn, M. Dating lava flows of tropical volcanoes by means of spatial modeling of vegetation recovery. Earth Surf. Process. Landf. 2017, 43, 840–856. [Google Scholar] [CrossRef]
- Zhou, J.; Fu, B.; Gao, G.; Lu, N.; Lü, Y.; Wang, S. Temporal stability of surface soil moisture of different vegetation types in the Loess Plateau of China. Catena 2015, 128, 1–15. [Google Scholar] [CrossRef]
- Sadri, S. A SMAP-Based Drought Monitoring Index for the United States. Hydrol. Earth Syst. Sci. Discuss 2018, 182, 1–19. [Google Scholar] [CrossRef]
- Jiao, Q.; Li, R.; Wang, F.; Mu, X.; Li, P.; An, C. Impacts of Re-Vegetation on Surface Soil Moisture over the Chinese Loess Plateau Based on Remote Sensing Datasets. Remote Sens. 2016, 8, 156. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Zhang, W.; Qi, J.; Li, F.-M. A regional evaluation of plastic film mulching for improving crop yields on the Loess Plateau of China. Agric. For. Meteorol. 2018, 248, 458–468. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, P.; Zhao, X.; Wang, J.; Shi, Y.; Zhang, B.; Tian, L.; Li, H. Estimation of spatial soil moisture averages in a large gully of the Loess Plateau of China through statistical and modeling solutions. J. Hydrol. 2013, 486, 466–478. [Google Scholar] [CrossRef]
- Tang, X.; Miao, C.; Xi, Y.; Duan, Q.; Lei, X.; Li, H. Analysis of precipitation characteristics on the loess plateau between 1965 and 2014, based on high-density gauge observations. Atmos. Res. 2018, 213, 264–274. [Google Scholar] [CrossRef]
- Xia, L.; Song, X.; Leng, P.; Wang, Y.; Hao, Y.; Wang, Y. A comparison of two methods for estimating surface soil moisture based on the triangle model using optical/thermal infrared remote sensing over the source area of the Yellow River. Int. J. Remote Sens. 2018, 40, 2120–2137. [Google Scholar] [CrossRef]














| Data Product | Variables Used | Use | Spatial/Temporal Resolution |
|---|---|---|---|
| MOD09GA | The temporal range for granule acquisition | Collecting the corresponding times of in situ RSM measurements | 500 m, 1 day |
| MOD09A1 | Surface reflectance | Calculating NDVI, ATI, and TVDI | 500 m, 8 day |
| MOD11A2 | Daytime/nighttime LST | Calculating TVDI and ATI | 1 km, 8 day |
| MCD12Q1. Type2 | Land covers | Producing a water body mask | 1 km, 1 year |
| Day | The Acquisition Times of the MODIS Granules | In Situ RSM Measurements | ||||||
|---|---|---|---|---|---|---|---|---|
| Time Range | h25v04 (UTC) | h25v05 (UTC) | h26v04 (UTC) | h26v05 (UTC) | h27v05 (UTC) | Time Range (UTC) | Daily RSM (%) | |
| 23 Apr. | Start time | 02:05:00 | 03:45:00 | 02:05:00 | 03:45:00 | 02:05:00 | 03:00:00 | 25.00 |
| End time | 05:30:00 | 05:30:00 | 03:50:00 | 03:55:00 | 03:55:00 | 06:00:00 | ||
| 24 Apr. | Start time | 02:45:00 | - | 01:10:00 | 02:50:00 | 02:50:00 | 02:00:00 | 25.00 |
| End time | 02:55:00 | - | 02:55:00 | 03:00:00 | 03:00:00 | 03:00:00 | ||
| 25 Apr. | Start time | 01:50:00 | 03:35:00 | 01:50:00 | 03:35:00 | 01:55:00 | 02:00:00 | 25.40 |
| End time | 05:15:00 | 05:20:00 | 03:40:00 | 05:20:00 | 03:40:00 | 06:00:00 | ||
| 26 Apr. | Start time | 02:35:00 | 04:15:00 | 00:55:00 | 02:40:00 | 02:35:00 | 01:00:00 | 26.00 |
| End time | 04:20:00 | 06:05:00 | 04:20:00 | 04:25:00 | 04:25:00 | 07:00:00 | ||
| 27 Apr. | Start time | 03:20:00 | 03:20:00 | 01:40:00 | 03:20:00 | 01:40:00 | 02:00:00 | 25.00 |
| End time | 05:05:00 | 05:10:00 | 03:25:00 | 05:05:00 | 03:30:00 | 06:00:00 | ||
| 28 Apr. | Start time | 02:25:00 | 04:05:00 | 00:45:00 | 02:25:00 | 02:25:00 | 01:00:00 | 25.00 |
| End time | 05:45:00 | 05:50:00 | 04:10:00 | 04:10:00 | 04:10:00 | 06:00:00 | ||
| 29 Apr. | Start time | 03:05:00 | 03:10:00 | 01:25:00 | 03:10:00 | 01:30:00 | 02:00:00 | 24.00 |
| End time | 04:55:00 | 04:55:00 | 04:50:00 | 04:55:00 | 03:15:00 | 05:00:00 | ||
| 30 Apr. | Start time | 02:10:00 | 03:50:00 | 02:10:00 | 02:15:00 | 02:15:00 | 03:00:00 | 26.00 |
| End time | 05:35:00 | 05:40:00 | 03:55:00 | 04:00:00 | 04:00:00 | 06:00:00 | ||
| 8-day average in situ RSM measurement (DOY: 113; Station: 52,765) | 25.18 | |||||||
| DOY | Month/ Season | Calibration | Validation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. of Stations | Model | ||||||||||
| 17 | Jan/Winter | 75 | ATI/TVDI | 0.03 | 0.15 | 0.21 | 0.51 | 0.67 | 5.06 ± 0.066 | 0.11 ± 0.038 | 0.57 ± 0.011 |
| 25 | Jan/Winter | 74 | ATI | 0.05 | 0.14 | 0.55 | 0.70 | 0.71 | 4.63 ± 0.067 | 0.03 ± 0.018 | 0.50 ± 0.018 |
| 41 | Feb/Winter | 86 | ATI | 0.00 | 0.15 | 0.22 | 0.17 | 0.59 | 4.47 ± 0.090 | 0.12 ± 0.068 | 0.36 ± 0.030 |
| 49 | Feb/Winter | 101 | ATI/TVDI | 0.06 | 0.14 | 0.64 | 0.62 | 0.45 | 5.23 ± 0.071 | 0.05 ± 0.041 | 0.38 ± 0.023 |
| 57 | Mar/Spring | 157 | ATI/TVDI | 0.09 | 0.19 | 0.26 | 0.92 | 0.57 | 5.46 ± 0.091 | 0.07 ± 0.036 | 0.36 ± 0.030 |
| 81 | Mar/Spring | 209 | ATI/TVDI | 0.10 | 0.18 | 0.21 | 0.94 | 0.92 | 3.07 ± 0.067 | 0.05 ± 0.031 | 0.52 ± 0.024 |
| 89 | Apr/Spring | 209 | ATI/TVDI | 0.14 | 0.17 | 0.22 | 0.81 | 0.80 | 3.63 ± 0.037 | 0.02 ± 0.014 | 0.23 ± 0.030 |
| 97 | Apr/Spring | 210 | ATI/TVDI | 0.11 | 0.21 | 0.31 | 0.90 | 0.92 | 3.75 ± 0.068 | 0.06 ± 0.032 | 0.20 ± 0.051 |
| 105 | Apr/Spring | 210 | ATI/TVDI | 0.12 | 0.21 | 0.35 | 0.92 | 0.86 | 4.59 ± 0.044 | 0.03 ± 0.018 | 0.25 ± 0.028 |
| 113 | Apr/Spring | 210 | ATI/TVDI | 0.15 | 0.18 | 0..21 | 0.94 | 0.92 | 3.70 ± 0.068 | 0.04 ± 0.022 | 0.48 ± 0.025 |
| 121 | May/Spring | 210 | ATI/TVDI | 0.17 | 0.22 | 0.27 | 0.97 | 0.83 | 4.43 ± 0.058 | 0.03 ± 0.022 | 0.44 ± 0.018 |
| 129 | May/Spring | 211 | ATI/TVDI | 0.33 | 0.50 | 0.70 | 0.81 | 0.73 | 4.52 ± 0.063 | 0.09 ± 0.047 | 0.62 ± 0.013 |
| 137 | May/Spring | 211 | ATI/TVDI | 0.26 | 0.36 | 0.52 | 0.87 | 0.04 | 3.43 ± 0.071 | 0.05 ± 0.025 | 0.73 ± 0.011 |
| 145 | May/Spring | 211 | ATI/TVDI | 0.20 | 0.38 | 0.57 | 0.85 | 0.83 | 4.62 ± 0.074 | 0.11 ± 0.060 | 0.44 ± 0.022 |
| 153 | Jun/Summer | 211 | ATI | 0.23 | 0.34 | 0.41 | 0.82 | 0.79 | 5.56 ± 0.042 | 0.02 ± 0.018 | 0.35 ± 0.016 |
| ATI/TVDI | 4.42 ± 0.070 | 0.12 ± 0.056 | 0.50 ± 0.020 | ||||||||
| 161 | Jun/Summer | 208 | TVDI | 0.29 | 0.49 | 0.69 | 0.76 | 0.55 | 5.59 ± 0.187 | 0.16 ± 0.085 | 0.34 ± 0.044 |
| ATI/TVDI | 5.39 ± 0.077 | 0.14 ± 0.048 | 0.23 ± 0.044 | ||||||||
| ATI | 5.22 ± 0.035 | 0.01 ± 0.009 | 0.54 ± 0.008 | ||||||||
| 169 | Jun/Summer | 211 | ATI/TVDI | 0.09 | 0.36 | 0.43 | 0.95 | 0.59 | 4.08 ± 0.060 | 0.07 ± 0.034 | 0.61 ± 0.015 |
| 177 | Jun/Summer | 211 | ATI/TVDI | 0.07 | 0.33 | 0.46 | 0.93 | 0.66 | 4.44 ± 0.039 | 0.02 ± 0.016 | 0.50 ± 0.013 |
| 185 | Jul/Summer | 213 | ATI/TVDI | 0.33 | 0.45 | 0.57 | 0.90 | 0.38 | 4.68 ± 0.038 | 0.03 ± 0.017 | 0.63 ± 0.006 |
| 193 | Jul/Summer | 212 | ATI/TVDI | 0.43 | 0.44 | 0.60 | 0.87 | 0.28 | 4.92 ± 0.065 | 0.08 ± 0.042 | 0.18 ± 0.041 |
| 209 | Jul/Summer | 212 | ATI/TVDI | 0.31 | 0.45 | 0.56 | 0.89 | 0.68 | 6.01 ± 0.127 | 0.05 ± 0.038 | 0.58 ± 0.020 |
| 217 | Aug/Summer | 213 | ATI/TVDI | 0.00 | 0.32 | 0.51 | 0.72 | 0.68 | 5.10 ± 0.094 | 0.04 ± 0.028 | 0.57 ± 0.020 |
| 233 | Aug/Summer | 213 | ATI/TVDI | 0.29 | 0.29 | 0.56 | 0.80 | 0.60 | 5.57 ± 0.101 | 0.08 ± 0.034 | 0.21 ± 0.036 |
| 249 | Sep/Autumn | 213 | ATI/TVDI | 0.24 | 0.36 | 0.50 | 0.85 | 0.82 | 6.02 ± 0.105 | 0.18 ± 0.062 | 0.37 ± 0.040 |
| ATI | 5.06 ± 0.135 | 0.12 ± 0.098 | 0.46 ± 0.049 | ||||||||
| 257 | Sep/Autumn | 213 | ATI/TVDI | 0.25 | 0.50 | 0.55 | 0.84 | 0.82 | 4.41 ± 0.053 | 0.16 ± 0.035 | 0.21 ± 0.021 |
| ATI | 5.59 ± 0.050 | 0.03 ± 0.030 | 0.32 ± 0.022 | ||||||||
| 265 | Sep/Autumn | 212 | ATI/TVDI | 0.11 | 0.20 | 0.31 | 0.81 | 0.86 | 4.99 ± 0.130 | 0.23 ± 0.077 | 0.50 ± 0.041 |
| 273 | Oct/Autumn | 212 | ATI/TVDI | 0.11 | 0.25 | 0.33 | 0.93 | 0.76 | 6.79 ± 0.212 | 0.17 ± 0.130 | 0.17 ± 0.060 |
| ATI | 4.00 ± 0.034 | 0.03 ± 0.020 | 0.43 ± 0.013 | ||||||||
| 281 | Oct/Autumn | 212 | ATI/TVDI | 0.28 | 0.31 | 0.38 | 0.58 | 0.75 | 4.79 ± 0.130 | 0.38 ± 0.071 | 0.47 ± 0.046 |
| 289 | Oct/Autumn | 212 | ATI/TVDI | 0.00 | 0.26 | 0.38 | 0.74 | 0.88 | 5.42 ± 0.024 | 0.04 ± 0.036 | 0.32 ± 0.018 |
| 297 | Oct/Autumn | 212 | ATI/TVDI | 0.25 | 0.25 | 0..33 | 0.82 | 0.75 | 3.31 ± 0.066 | 0.03 ± 0.027 | 0.67 ± 0.014 |
| 305 | Nov/Autumn | 212 | ATI/TVDI | 0.02 | 0.17 | 0.26 | 0.51 | 0.84 | 3.95 ± 0.036 | 0.02 ± 0.025 | 0.45 ± 0.014 |
| 313 | Nov/Autumn | 213 | ATI/TVDI | 0.00 | 0.22 | 0.25 | 0.51 | 0.77 | 2.83 ± 0.039 | 0.05 ± 0.031 | 0.75 ± 0.008 |
| 321 | Nov/Autumn | 189 | ATI/TVDI | 0.20 | 0.20 | 0.23 | 0.72 | 0.53 | 3.84 ± 0.046 | 0.05 ± 0.034 | 0.47 ± 0.014 |
| 329 | Nov/Autumn | 185 | ATI/TVDI | 0.17 | 0.23 | 0.31 | 0.70 | 0.60 | 4.35 ± 0.054 | 0.19 ± 0.051 | 0.67 ± 0.008 |
| 337 | Dec/Winter | 185 | ATI/TVDI | 0.00 | 0.23 | 0.31 | 0.40 | 0.36 | 4.72 ± 0.066 | 0.25 ± 0.056 | 0.64 ± 0.010 |
| 345 | Dec/Winter | 185 | ATI/TVDI | 0.08 | 0.20 | 0.32 | 0.68 | 0.65 | 4.60 ± 0.069 | 0.04 ± 0.017 | 0.54 ± 0.017 |
| 353 | Dec/Winter | 185 | ATI/TVDI | 0.03 | 0.19 | 0.22 | 0.45 | 0.56 | 4.54 ± 0.045 | 0.03 ± 0.021 | 0.60 ± 0.010 |
| ATI/TVDI | 0.03 | 0.25 | 0.35 | 3.86 ± 0.026 | 0.04 ± 0.034 | 0.61 ± 0.007 | |||||
| 361 | Dec/Winter | 182 | TVDI | 0.04 | 0.16 | 0.18 | 0.82 | 0.84 | 5.09 ± 0.041 | 0.02 ± 0.012 | 0.32 ± 0.018 |
| ATI/TVDI | 4.89 ± 0.166 | 0.50 ± 0.066 | 0.52 ± 0.025 | ||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, L.; Li, L.; Zhang, T.; Chen, L.; Zhao, J.; Hu, S.; Cheng, L.; Liu, W. Soil Moisture Estimation for the Chinese Loess Plateau Using MODIS-derived ATI and TVDI. Remote Sens. 2020, 12, 3040. https://doi.org/10.3390/rs12183040
Yuan L, Li L, Zhang T, Chen L, Zhao J, Hu S, Cheng L, Liu W. Soil Moisture Estimation for the Chinese Loess Plateau Using MODIS-derived ATI and TVDI. Remote Sensing. 2020; 12(18):3040. https://doi.org/10.3390/rs12183040
Chicago/Turabian StyleYuan, Lina, Long Li, Ting Zhang, Longqian Chen, Jianlin Zhao, Sai Hu, Liang Cheng, and Weiqiang Liu. 2020. "Soil Moisture Estimation for the Chinese Loess Plateau Using MODIS-derived ATI and TVDI" Remote Sensing 12, no. 18: 3040. https://doi.org/10.3390/rs12183040
APA StyleYuan, L., Li, L., Zhang, T., Chen, L., Zhao, J., Hu, S., Cheng, L., & Liu, W. (2020). Soil Moisture Estimation for the Chinese Loess Plateau Using MODIS-derived ATI and TVDI. Remote Sensing, 12(18), 3040. https://doi.org/10.3390/rs12183040