Assessing Canopy Responses to Thinnings for Sweet Chestnut Coppice with Time-Series Vegetation Indices Derived from Landsat-8 and Sentinel-2 Imagery
Abstract
:1. Introduction
2. Materials and Methods
2.1. Forest and Field Data
2.2. LAI Field Measurements
2.3. Satellite Data
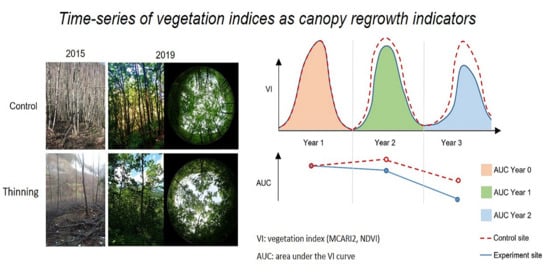
2.4. Comparing Canopy Evolution before and after the Treatments
3. Results
3.1. Regression Between VIs as Proxies of LAIe
3.2. Canopy Evolution before and after the Treatments
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nabuurs, G.J.; Verkerk, P.J.; Schelhaas, M.; González-Olabarria, J.R.; Trasobares, A.; Cienciala, E. Climate-Smart Forestry: Mitigation implact in Three European Regions; European Forest Institute: Joensuu, Finland, 2018. [Google Scholar]
- Köhl, M.; Ehrhart, H.P.; Knauf, M.; Neupane, P.R. A Viable Indicator Approach for Assessing Sustainable Forest Management in Terms of Carbon Emissions and Removals. Ecol. Indic. 2020, 111, 106057. [Google Scholar] [CrossRef]
- Fang, H.; Ye, Y.; Liu, W.; Wei, S.; Ma, L. Continuous Estimation of Canopy Leaf Area Index (LAI) and Clumping Index over Broadleaf Crop Fields: An Investigation of the PASTIS-57 Instrument and Smartphone Applications. Agric. Meteorol. 2018, 253, 48–61. [Google Scholar] [CrossRef]
- Bréda, N.J.J. Leaf area index. In Encyclopedia of Ecology; Erik, S., Brian, F., Eds.; Academic Press: Oxford, UK, 2008; pp. 2148–2154. [Google Scholar]
- GCOS. The Global Observing System for Climate: Implementation Needs (GCOS-200). Available online: https://library.wmo.int/doc_num.php?explnum_id=3417 (accessed on 20 April 2016).
- Chen, J.M.; Black, T.A. Defining Leaf Area Index for Non-Flat Leaves. Plant. Cell. Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Alton, P.B. The Sensitivity of Models of Gross Primary Productivity to Meteorological and Leaf Area Forcing: A Comparison between a Penman-Monteith Ecophysiological Approach and the MODIS Light-Use Efficiency Algorithm. Agric. For. Meteorol. 2016, 218, 11–24. [Google Scholar] [CrossRef] [Green Version]
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and Indirect Estimation of Leaf Area Index, fAPAR, and Net Primary Production of Terrestrial Ecosystems. Remote Sens. Environ. 1999, 70, 29–51. [Google Scholar] [CrossRef]
- Chen, J.M.; Pavlic, G.; Brown, L.; Cihlar, J.; Leblanc, S.G.; White, H.P.; Hall, R.J.; Peddle, D.R.; King, D.J.; Trofymow, J.A.; et al. Derivation and Validation of Canada-Wide Leaf Area Index Maps Using Ground Measurements and High and Moderate Resolution Satellite Imagery. Remote Sens. Environ. 2002, 80, 165–184. [Google Scholar] [CrossRef]
- Pearse, G.D. Estimating Leaf Area Index from Airborne Laser Scanning in Pinus radiata Forests. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2017. [Google Scholar]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of Methods for In Situ Leaf Area Index Determination: Part, I. Theories, Sensors and Hemispherical Photography. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Nackaerts, K.; Coppin, P.; Muys, B.; Hermy, M. Sampling Methodology for LAI Measurements with LAI-2000 in Small Forest Stands. Agric. For. Meteorol. 2000, 101, 247–250. [Google Scholar] [CrossRef]
- Davi, H.; Baret, F.; Huc, R.; Dufrêne, E. Effect of Thinning on LAI Variance in Heterogeneous Forests. For. Ecol. Manag. 2008, 256, 890–899. [Google Scholar] [CrossRef]
- Cutini, A.; Matteucci, G.; Mugnozza, G.S. Estimation of Leaf Area Index with the Li-Cor LAI 2000 in Deciduous Forests. For. Ecol. Manag. 1998, 105, 55–65. [Google Scholar] [CrossRef]
- Le Dantec, V.; Dufrêne, E.; Saugier, B. Interannual and Spatial Variation in Maximum Leaf Area Index of Temperate Deciduous Stands. For. Ecol. Manag. 2000, 134, 71–81. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.J.; Jonckheere, I.; Coppin, P. Review of Methods for In Situ Leaf Area Index (LAI) Determination Part II. Estimation of LAI, Errors and Sampling. Agric. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef] [Green Version]
- Pearse, G.D.; Watt, M.S.; Morgenroth, J. Comparison of Optical LAI Measurements under Diffuse and Clear Skies after Correcting for Scattered Radiation. Agric. For. Meteorol. 2016, 221, 61–70. [Google Scholar] [CrossRef]
- Tesfamichael, S.G.; van Aardt, J.; Roberts, W.; Ahmed, F. Retrieval of Narrow-Range LAI of at Multiple Lidar Point Densities: Application on Eucalyptus grandis Plantation. Int. J. Appl. Earth. Obs. 2018, 70, 93–104. [Google Scholar] [CrossRef]
- Wulder, M.A. Remote Sensing of Forest Environments; Franklin, S.E., Ed.; Springer: Boston, MA, USA, 2003; ISBN 978-1-4613-5014-9. [Google Scholar]
- Bannari, D.; Morin, F.; Bonn, A.R. Huete “A Review of Vegetation Indices”. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S. Leaf Area Index Models. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Hornero, A.; Hernández-Clemente, R.; North, P.R.J.; Beck, P.S.A.; Boscia, D.; Navas-Cortes, J.A.; Zarco-Tejada, P.J. Monitoring the Incidence of Xylella fastidiosa Infection in Olive Orchards Using Ground-Based Evaluations, Airborne Imaging Spectroscopy and Sentinel-2 Time Series through 3-D Radiative Transfer Modelling. Remote Sens. Environ. 2020, 236, 111480. [Google Scholar] [CrossRef]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global Mapping of Foliage Clumping Index Using Multi-Angular Satellite Data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- Korhonen, L.; Packalen, P.; Rautiainen, M. Comparison of Sentinel-2 and Landsat 8 in the Estimation of Boreal Forest Canopy Cover and Leaf Area Index. Remote Sens. Environ. 2017, 195, 259–274. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Measuring Leaf Area Index of Plant Canopies with Branch Architecture. Agric. For. Meteorol. 1991, 57, 1–12. [Google Scholar] [CrossRef]
- Tillack, A.; Clasen, A.; Kleinschmit, B.; Förster, M. Estimation of the Seasonal Leaf Area Index in An Alluvial Forest Using High-Resolution Satellite-Based Vegetation Indices. Remote Sens. Environ. 2014, 141, 52–63. [Google Scholar] [CrossRef]
- Brantley, S.T.; Zinnert, J.C.; Young, D.R. Application of Hyperspectral Vegetation Indices to Detect Variations in High Leaf Area Index Temperate Shrub Thicket Canopies. Remote Sens. Environ. 2011, 115, 514–523. [Google Scholar] [CrossRef] [Green Version]
- Meyer, L.H.; Heurich, M.; Beudert, B.; Premier, J.; Pflugmacher, D. Comparison of Landsat-8 and Sentinel-2 Data for Estimation of Leaf Area Index in Temperate Forests. Remote Sens. 2019, 11, 1160. [Google Scholar] [CrossRef] [Green Version]
- Ricci, G.F.; Romano, G.; Leronni, V.; Gentile, F. Effect of Check Dams on Riparian Vegetation Cover: A Multiscale Approach Based on Field Measurements and Satellite Images for Leaf Area Index Assessment. Sci. Total. Environ. 2019, 657, 827–838. [Google Scholar] [CrossRef] [PubMed]
- Le Maire, G.; Marsden, C.; Nouvellon, T.; Grinand, C.; Hakamada, R.; Stape, J.L. MODIS NDVI Time-Series Allow the Monitoring of Eucalyptus Plantation Biomass. Remote Sens. Environ. 2011, 115, 2613–2625. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting Trend and Seasonal Changes in Satellite Image Time Series. Remote Sens. Environ. 2010, 106–115. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological Change Detection While Accounting for Abrupt and Gradual Trends in Satellite Image Time Series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef] [Green Version]
- Verbesselt, J.; Zeileis, A.; Herold, M. Near Real-Time Disturbance Detection Using Satellite Image Time Series. Remote Sens. Environ. 2012, 123, 98–108. [Google Scholar] [CrossRef]
- Manetti, M.C.; Amorini, E.; Becagli, C.; Conedera, M.; Giudici, F. Productive Potential of Chestnut (Castanea Sativa Mill.) Stands in Europe. Snow. Landsc. Res. 2001, 76, 471–476. [Google Scholar]
- Manetti, M.C.; Marcolin, E.; Pividori, M.; Zanuttini, R.; Conedera, M. Coppice Woodlands and Chestnut Wood Technology. In The Chestnut Handbook; Crop and Forest Management; Beccaro, G., Alma, A., Bounous, G., Gomes-Laranjo, J., Eds.; CRC Press, Taylor & Francis Group: Oxfordshire, UK, 2020; pp. 275–295. [Google Scholar]
- Prada, M.; González-García, M.; Majada, J.; Martínez-Alonso, C. Development of a Dynamic Growth Model for Sweet Chestnut Coppice: A Case Study in Northwest Spain. Ecol. Model. 2019, 409, 108761. [Google Scholar] [CrossRef]
- Prendes, C.; Bujan, S.; Ordóñez Galán, C.; Canga, E. Large Scale Semi-Automatic Detection of Forest Roads from Low Density LiDAR Data on Steep Terrain in Northern Spain. IFOREST 2019, 12, 366–374. [Google Scholar] [CrossRef] [Green Version]
- Solberg, S.; Brunner, A.; Hanssen, K.H.; Lange, H.; Næsset, E.; Rautiainen, M.; Stenberg, P. Mapping LAI in A Norway Spruce Forest Using Airborne Laser Scanning. Remote Sens. Environ. 2009, 113, 2317–2327. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- GEE. Available online: https://developers.google.com/earth-engine/datasets/catalog/LANDSAT_LC08_C01_T1_SR (accessed on 17 April 2020).
- GEE. Available online: https://developers.google.com/earth-engine/datasets/catalog/COPERNICUS_S2_SR (accessed on 17 April 2020).
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the Relationship of NDVI with Leaf Area Index in A Deciduous Forest Site. Remote Sens. Environ. 2005, 94, 244–255. [Google Scholar] [CrossRef]
- Huang, S.; Tang, L.; Hupy, J.P.; Wang, Y.; Shao, G.A. A Commentary Review on the Use of Normalized Difference Vegetation Index (NDVI) in the Era of Popular Remote Sensing. J. Res. 2020. [Google Scholar] [CrossRef]
- Huete, A. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of Soil-Adjusted Vegetation Indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A Modified Soil Adjusted Vegetation Index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote. Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Greenwave Effect) of Natural Vegetation; Remote Sensing Center Texas A&M University: College Station, TX, USA, 1974. [Google Scholar]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The Next Landsat Satellite: The Landsat Data Continuity Mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Meygret, A. Sentinel-2: ESA’s optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing Prediction Power and Stability of Broadband and Hyperspectral Vegetation Indices for Estimation of Green Leaf Area index and Canopy Chlorophyll Density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Valentini, R. Relationships between NDVI, Canopy Structure, and Photosynthesis in Three Californian Vegetation Types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef] [Green Version]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1978, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Veraverbeke, S.; Gitas, I.; Katagis, T.; Polychronaki, A.; Somers, B.; Goossens, R. Assessing Post-Fire Vegetation Recovery Using Red–Near Infrared Vegetation Indices: Accounting for Background and Vegetation Variability. ISPRS. J. Photogramm. 2012, 68, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Viedma, O.; Meliá, J.; Segarra, D.; García-Haro, J. Modelling Rates of Ecosystem Recovery After Fires by Using Landsat TM Data. Remote Sens. Environ. 1997, 61, 383–398. [Google Scholar] [CrossRef]
- Nilson, T.; Peterson, U. Age Dependence of Forest Reflectance: Analysis of Main Driving Factors. Remote Sens. Environ. 1994, 48, 319–331. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of Global Leaf Area Index and Absorbed PAR Using Radiative Transfer Models. IEEET Geosci. Remote 1997, 35, 1380–1393. [Google Scholar] [CrossRef] [Green Version]
- Zhongming, W.; Lees, B.G.; Feng, J.; Wanning, L.; Haijing, S. Stratified Vegetation Cover Index: A New Way to Assess Vegetation Impact On Soil Erosion. Catena 2010, 83, 87–93. [Google Scholar] [CrossRef]
- Jinguo, Y.; Wei, W. Identification of Forest Vegetation Using Vegetation Indices. Chin. J. Popul. Resour. Environ. 2013, 2, 12–16. [Google Scholar] [CrossRef]
- Pretzsch, H. Forest Dynamics, Growth and Yield: From Measurement to Model; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Profft, I.; Mund, M.; Weber, G.E.; Weller, E.; Schulze, E.D. Forest Management and Carbon Sequestration in Wood Products. Eur. J. For. Res. 2009, 128, 399–413. [Google Scholar] [CrossRef] [Green Version]
- Prada, M.; Bravo, F.; Berdasco, L.; Canga, E.; Martínez-Alonso, C. Carbon Sequestration for Different Management Alternatives in Sweet Chestnut Coppice in Northern Spain. J. Clean. Prod. 2016, 135, 1161–1169. [Google Scholar] [CrossRef]








| Trial 1 | Trial 2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Control | Treatment 1 | Treatment 2 | Control | Treatment 1 | |||||||||
| BT/AT | AT | BT | AT | AT | BT | AT | AT | BT/AT | AT | BT | AT | AT | |
| Year | 2015 | 2019 | 2015 | 2015 | 2019 | 2015 | 2015 | 2019 | 2015 | 2019 | 2015 | 2015 | 2019 |
| t | 16 | 19 | 16 | 16 | 19 | 16 | 16 | 19 | 13 | 16 | 13 | 13 | 16 |
| N | 2843 | 2660 | 4484 | 933 | 905 | 3664 | 439 | 439 | 3338 | 3169 | 3756 | 622 | 545 |
| G | 21.5 | 22.9 | 21.2 | 10.6 | 11.5 | 29.8 | 5.8 | 7.04 | 13.9 | 15.4 | 21.1 | 4.7 | 5.4 |
| Dm | 9.5 | 10.2 | 9.0 | 11.9 | 12.6 | 9.8 | 12.7 | 14.0 | 7.4 | 7.9 | 8.3 | 10.5 | 11.8 |
| V | 92.5 | 116.3 | - | 63.9 | 71.0 | - | 36.8 | 45.4 | 52.5 | 66.5 | - | 19.8 | 26.5 |
| Trial 1 | Trial 2 | ||||
|---|---|---|---|---|---|
| Control | Treatment 1 | Treatment 2 | Control | Treatment 1 | |
| LAIe | 2.78 | 1.57 | 1.56 | 2.75 | 2.11 |
| n LAI | 2 | 6 | 8 | 4 | 23 |
| Vegetation Index | Equation | Reference |
|---|---|---|
| Normalized Difference Vegetation Index | [50] | |
| Soil adjusted vegetation index | [46] | |
| Modified Soil-Adjusted Vegetation Index | [48] | |
| Optimized Soil-Adjusted Vegetation Index | [47] | |
| First modified triangular vegetation index | [49] | |
| Second modified triangular vegetation index | [49] | |
| First Modified Chlorophyll Absorption Ratio Index | [49] | |
| Second Modified Chlorophyll Absorption Ratio Index | [49] |
| Trial1 | Trial 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| L8 | S2 | L8 | S2 | |||||
| VI | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE |
| MCARI2 | 0.74 | 0.20 | 0.72 | 0.21 | 0.61 | 0.29 | 0.75 | 0.24 |
| MTVI2 | 0.74 | 0.20 | 0.72 | 0.22 | 0.61 | 0.29 | 0.75 | 0.24 |
| OSAVI | 0.69 | 0.22 | 0.70 | 0.22 | 0.59 | 0.29 | 0.77 | 0.23 |
| SAVI | 0.68 | 0.22 | 0.63 | 0.24 | 0.55 | 0.31 | 0.74 | 0.24 |
| MTVI1 | 0.67 | 0.22 | 0.65 | 0.23 | 0.57 | 0.30 | 0.71 | 0.26 |
| MCARI1 | 0.67 | 0.22 | 0.65 | 0.23 | 0.57 | 0.30 | 0.71 | 0.26 |
| MSAVI | 0.67 | 0.23 | 0.63 | 0.24 | 0.54 | 0.31 | 0.74 | 0.25 |
| NDVI | 0.24 | 0.34 | 0.75 | 0.20 | 0.26 | 0.40 | 0.80 | 0.22 |
| Trial 1 | Trial 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| T1-C | T2-C | T1-T2 | T1-C | ||||||
| L8 | S2 | L8 | S2 | L8 | S2 | L8 | S2 | ||
| MCARI2 | 2016 | X | X | X | X | X | X | X | X |
| 2017 | -. | -. | X | X | X | X | X | X | |
| 2018 | -. | -. | X | X | -. | -. | -. | X | |
| 2019 | -. | -. | -. | -. | -. | -. | -. | X | |
| NDVI | 2016 | -. | X | X | X | X | -. | X | X |
| 2017 | X | -. | X | -. | -. | -. | X | X | |
| 2018 | X | -. | X | -. | -. | -. | -. | X | |
| 2019 | - | - | - | - | - | - | - | X | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prada, M.; Cabo, C.; Hernández-Clemente, R.; Hornero, A.; Majada, J.; Martínez-Alonso, C. Assessing Canopy Responses to Thinnings for Sweet Chestnut Coppice with Time-Series Vegetation Indices Derived from Landsat-8 and Sentinel-2 Imagery. Remote Sens. 2020, 12, 3068. https://doi.org/10.3390/rs12183068
Prada M, Cabo C, Hernández-Clemente R, Hornero A, Majada J, Martínez-Alonso C. Assessing Canopy Responses to Thinnings for Sweet Chestnut Coppice with Time-Series Vegetation Indices Derived from Landsat-8 and Sentinel-2 Imagery. Remote Sensing. 2020; 12(18):3068. https://doi.org/10.3390/rs12183068
Chicago/Turabian StylePrada, Marta, Carlos Cabo, Rocío Hernández-Clemente, Alberto Hornero, Juan Majada, and Celia Martínez-Alonso. 2020. "Assessing Canopy Responses to Thinnings for Sweet Chestnut Coppice with Time-Series Vegetation Indices Derived from Landsat-8 and Sentinel-2 Imagery" Remote Sensing 12, no. 18: 3068. https://doi.org/10.3390/rs12183068
APA StylePrada, M., Cabo, C., Hernández-Clemente, R., Hornero, A., Majada, J., & Martínez-Alonso, C. (2020). Assessing Canopy Responses to Thinnings for Sweet Chestnut Coppice with Time-Series Vegetation Indices Derived from Landsat-8 and Sentinel-2 Imagery. Remote Sensing, 12(18), 3068. https://doi.org/10.3390/rs12183068