Statistical Analysis of 1996–2017 Ozone Profile Data Obtained by Ground-Based Microwave Radiometry
Abstract
:1. Introduction
2. Equipment, Measurements, and Data Processing
3. Statistical Analysis
3.1. Statistical Parameters and Method of Errors Correction
3.2. Statistical Parameters of Retrieval Errors
3.3. Probability Distributions of Ozone Variations in Two Decades (1996–2006 and 2007–2017)
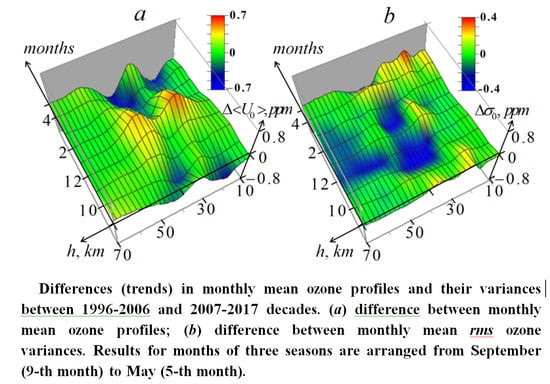
3.4. Mean and Variances of Retrieved Ozone Profiles in Separate Months of Two Decades (1996–2006 and 2007–2017)
3.5. Inter-altitude and Time Covariance and Correlation Functions in Separate Months of Two Decades (1996–2006 and 2007–2017); Frequency Spectra of Time Covariance and Correlation Functions
3.6. Integral Statistical Parameters of Ozone Profiles of Two Decades (1996–2006 and 2007–2017).
3.7. Comparison of Results with Other Research
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Inverse Problem of Microwave Radiometry Ozone Profiling
- (a)
- Formation of the simulated ozone profile;
- (b)
- Computations of the spectrum of brightness temperature;
- (c)
- Adding of simulated Gaussian random errors with zero mean value and preset mean-square variations ;
- (d)
- Solving the inverse problem (9);
- (e)
- Comparison of the retrieved and simulated ozone profiles.
References
- SPARC/IO3C/GAW Report on Long-Term Ozone Trends and Uncertainties in the Stratosphere; SPARC Report No. 9; Petropavlovskikh, I.; Godin-Beekmann, S.; Hubert, D.; Damadeo, R.; Hassler, B.; Sofieva, V. (Eds.) SPARC: Richmond, VA, USA, 2019; Available online: http://www.sparc-climate.org/publications/sparc-reports (accessed on 10 October 2020). [CrossRef]
- Steinbrecht, W.; Froidevaux, L.; Fuller, R.; Wang, R.; Anderson, J.; Roth, C.; Bourassa, A.E.; Degenstein, D.A.; Damadeo, R.; Jones, N.B.; et al. An update on ozone profile trends for the period 2000 to 2016. Atmos. Chem. Phys. 2017, 17, 10675–10690. [Google Scholar] [CrossRef] [Green Version]
- Manney, G.L.; Lawrence, Z.D.; Santee, M.L.; Livesey, N.J.; Lambert, A.; Pitts, M.C. Polar processing in a split vortex: Arctic ozone loss in early winter 2012/2013. Atmos. Chem. Phys. 2015, 15, 5381–5403. [Google Scholar] [CrossRef] [Green Version]
- Tao, M.; Konopka, P.; Ploeger, F.; Grooß, J.-U.; Müller, R.; Volk, C.M.; Walker, K.A.; Riese, M. Impact of the 2009 major sudden stratospheric warming on the composition of the stratosphere. Atmos. Chem. Phys. 2015, 15, 8695–8715. [Google Scholar] [CrossRef] [Green Version]
- Smyshlyaev, S.P.; Pogorel’tsev, A.I.; Galin, V.Y.; Drobashevskaya, E.A. Influence of wave activity on the composition of the polar stratosphere. Geomagn. Aeron. Engl. Transl. 2016, 56, 95–109. [Google Scholar] [CrossRef]
- Wang, W.; Tian, W.; Dhomse, S.; Xie, F.; Shu, J.; Austin, J. Stratospheric ozone depletion from future nitrous oxide increases. Atmos. Chem. Phys. 2014, 14, 12967–12982. [Google Scholar] [CrossRef] [Green Version]
- Manney, G.L.; Santee, M.L.; Rex, M.; Livesey, N.J.; Pitts, M.C.; Veefkind, P.; Nash, E.R.; Wohltmann, I.; Lehmann, R.; Poole, L.R.; et al. Unprecedented Arctic ozone loss in 2011. Nature 2011, 478, 469–475. [Google Scholar] [CrossRef]
- Kulikov, U.U.; Markina, N.N.; Naumov, A.P.; Riskin, V.G.; Sumin, M.I. Retrieval of Height Ozone Distribution by Ground-Based Measurements of Integral Absorption in the Millimeter Range. Atmos. Ocean. Phys. 1988, 24, 1282–1292. [Google Scholar]
- Gaikovich, K.P.; Kropotkina, E.P.; Solomonov, S.V. Vertical ozone profile determination from ground-based measurements of atmosphere millimeter-wave radiation. Izv. Atmos. Ocean. Phys. 1999, 35, 78–86. [Google Scholar]
- Solomonov, S.V.; Gaikovich, K.P.; Kropotkina, E.P.; Rozanov, S.B.; Lukin, A.N.; Ignat’ev, A.N. Remote sensing of atmospheric ozone at millimeter waves. Radiophys. Quantum Electron. 2011, 54, 102–110. [Google Scholar] [CrossRef]
- Fernandez, S.; Rufenacht, R.; Kampfer, N.; Portafaix, T.; Posny, F.; Payen, G. Results from the validation campaign of the ozone radiometer GROMOS-C at the NDACC station of Reunion island. Atmos. Chem. Phys. 2016, 16, 7531–7543. [Google Scholar] [CrossRef] [Green Version]
- Kropotkina, E.P.; Rozanov, S.B.; Lukin, A.N.; Ignat’ev, A.N.; Solomonov, S.V. Characteristics of Changes in the Ozone Content in the Upper Stratosphere over Moscow during the Cold Half-Years of 2014–2015 and 2015–2016. Geomagn. Aeron. 2017, 57, 361–368. [Google Scholar] [CrossRef]
- Solomonov, S.V.; Rozanov, S.B.; Kropotkina, E.P.; Lukin, A.N. A millimeter-wave spectroradiometer for the remote sensing of atmospheric ozone. J. Commun. Technol. Electron. 2000, 45, 1377–1382. [Google Scholar]
- Solomonov, S.V.; Ignat’ev, A.N.; Kropotkina, E.P.; Logvinenko, S.V.; Lukin, A.N.; Nikiforov, P.L.; Rozanov, S.B. Spectral instrumentation for monitoring atmospheric ozone at millimeter waves. Instrum. Exp. Tech. 2009, 52, 280–286. [Google Scholar] [CrossRef]
- Solomonov, S.V.; Kropotkina, E.P.; Lukin, A.N.; Ponomarenko, N.I.; Rozanov, S.B.; Ellder, J. Some features of the vertical ozone distribution from millimeter wave measurements at Pushchino and Onsala observatories. J. Atmos. Terr. Phys. 1994, 56, 9–15. [Google Scholar] [CrossRef]
- Gaikovich, K.P. Tikhonov’s Method of the Ground-based Radiometric Retrieval of the Ozone Profile, IGARSS’94 Digest. In Proceedings of the IGARSS’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; Volume 4, pp. 1901–1903. [Google Scholar]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; Winston: New York, NY, USA, 1977. [Google Scholar]
- Chahine, M.T. Inverse Problems in Radiative Transfer: Determination of Atmospheric Parameters. J. Atmos. Sci. 1970, 27, 960–967. [Google Scholar] [CrossRef]
- Waters, J.W.; Hardy, J.O.; Jarnot, R.F.; Picket, H.H. Chlorine Monoxide Radical, Ozone and Hydrogen Peroxide. Science 1981, 214, 61–64. [Google Scholar] [CrossRef]
- Rodgers, C.D. Characterization and Error Analyses of Profiles Retrieved from Remote Sensing Measurements. J. Geophys. Res. D Atmos. 1990, 95, 5587–5595. [Google Scholar] [CrossRef]
- Brillet, J. A Theoretical Study of Ozone Measurements Made with Ground-based Microwave Sensors. J. Geophys. Res. D Atmos. 1989, 94, 12833–12850. [Google Scholar] [CrossRef]
- Gaikovich, K.P.; Kitaj, S.D.; Naumov, A.P. On Determination of Ozone and Other Minor Gases of the Atmosphere by Limb-Viewing Measurements from Satellites in the Microwave Range. Russ. J. Remote Sens. 1991, 3, 73–81. [Google Scholar]
- Gaikovich, K.P. Inverse Problems in Physical Diagnostics; Nova Science Publishers Inc.: New York, NY, USA, 2004. [Google Scholar]
- Scientific Assessment of Ozone Depletion: 2018, World Meteorological Organization, Global Ozone Research and Monitoring Project—Report No.58, Geneva. 2018. Available online: https://www.esrl.noaa.gov/csl/assessments/ozone/2018/ (accessed on 10 October 2020).
- Froidevaux, L.; Livesey, N.J.; Read, W.G.; Jiang, Y.B.; Jimenez, C.; Filipiak, M.J.; Schwartz, M.J.; Santee, M.L.; Pumphrey, H.C.; Wu, D.L.; et al. Early validation analyses of atmospheric profiles from EOS MLS on the Aura satellite. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1106–1121. [Google Scholar] [CrossRef]
- Rozanov, S.B.; Solomonov, S.V.; Kropotkina, E.P.; Ignatyev, A.N.; Lukin, A.N. Ground-based remote sensing of the atmospheric ozone over Moscow at millimeter waves. Proc. SPIE 2006, 6362, U472–U482. [Google Scholar]
- Rozanov, S.B.; Zavgorodniy, A.S.; Solomonov, S.V.; Kropotkina, E.P.; Lukin, A.N.; Ignatyev, A.N. Microwave measurements of stratospheric and mesospheric ozone in Moscow. In Proceedings of the IGARSS 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3116–3119. [Google Scholar]
- Moreira, L.; Hocke, K.; Eckert, E.; von Clarmann, T.; Kämpfer, N. Trend analysis of stratospheric ozone profiles observed by GROMOS microwave radiometer at Bern. Atmos. Chem. Phys. 2015, 15, 10999–11009. [Google Scholar] [CrossRef] [Green Version]
- Scientific Assessment of Ozone Depletion: 2014, World Meteorological Organization, Global Ozone Research and Monitoring Project—Report No.55, Geneva. 2014. Available online: https://www.esrl.noaa.gov/csl/assessments/ozone/2014 (accessed on 10 October 2020).
- Zvyagintsev, A.M.; Vargin, P.N.; Peshin, S. Total ozone variations and trends during the period 1979–2014. Atmos. Ocean. Opt. 2015, 28, 575–584. [Google Scholar] [CrossRef]
- Grytsai, A.; Evtushevsky, O.; Klekociuk, A.; Milinevsky, G.; Yampolsky, Y.; Ivaniha, O.; Wang, Y. Investigations of the vertical influence of the 11-year solar cycle on ozone using SBUV and Antarctic ground-based measurements and CMIP6 forcing data. Atmosphere 2020, 11, 873. [Google Scholar] [CrossRef]
- Solomonov, S.V.; Kropotkina, E.P.; Rozanov, S.B.; Ignat’ev, A.N.; Lukin, A.N. Influence of strong sudden stratospheric warmings on ozone in the middle stratosphere according to millimeter wave observations. Geomagn. Aeron. 2017, 57, 361–368. [Google Scholar] [CrossRef]























Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaikovich, K.P.; Kropotkina, E.P.; Rozanov, S.B. Statistical Analysis of 1996–2017 Ozone Profile Data Obtained by Ground-Based Microwave Radiometry. Remote Sens. 2020, 12, 3374. https://doi.org/10.3390/rs12203374
Gaikovich KP, Kropotkina EP, Rozanov SB. Statistical Analysis of 1996–2017 Ozone Profile Data Obtained by Ground-Based Microwave Radiometry. Remote Sensing. 2020; 12(20):3374. https://doi.org/10.3390/rs12203374
Chicago/Turabian StyleGaikovich, Konstantin P., Elena P. Kropotkina, and Sergey B. Rozanov. 2020. "Statistical Analysis of 1996–2017 Ozone Profile Data Obtained by Ground-Based Microwave Radiometry" Remote Sensing 12, no. 20: 3374. https://doi.org/10.3390/rs12203374
APA StyleGaikovich, K. P., Kropotkina, E. P., & Rozanov, S. B. (2020). Statistical Analysis of 1996–2017 Ozone Profile Data Obtained by Ground-Based Microwave Radiometry. Remote Sensing, 12(20), 3374. https://doi.org/10.3390/rs12203374