Robust Statistical Detection of GNSS Multipath Using Inter-Frequency C/N0 Differences
Abstract
:1. Introduction
2. Methods
2.1. Multipath Detection Based on C/N0 Difference
2.2. Least Absolute Deviation and Quantile Regression
2.3. Iteratively Re-Weighted Least Squares
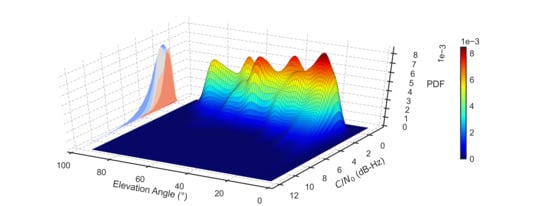
3. Determination of Multipath Detection Threshold
3.1. Modeling of Reference Functions Based on LAD
3.2. Distribution of Detection Statistics
3.3. A Robust Multipath Detection Method for Skewed Data
4. Performance Verification
4.1. Static Observation
4.2. Kinematic Observation
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pirsiavash, A.; Broumandan, A.; Lachapelle, G. Characterization of signal quality monitoring techniques for multipath detection in GNSS applications. Sensors 2017, 17, 1579. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Wang, H.; Yang, J.; He, L. GPS short-delay multipath estimation and mitigation based on least square method. J. Syst. Eng. Electr. 2009, 20, 954–961. [Google Scholar]
- Teunissen, P.T.J.; Montenbruck, O. Handbook of Global Navigation Satellite Systems; Springer: Berlin, Germany, 2017. [Google Scholar]
- Groves, P.D.; Jiang, Z.; Skelton, B.; Cross, P.A.; Lau, L.; Adane, Y.; Kale, I. Novel multipath mitigation methods using a dual-polarization antenna. In Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2010), Portland, OR, USA, 21–24 September 2010; pp. 140–151. [Google Scholar]
- Lau, L.; Cross, P. Development and testing of a new ray-tracing approach to GNSS carrier-phase multipath modelling. J. Geod. 2007, 81, 713–732. [Google Scholar] [CrossRef]
- Hsu, L.-T. GNSS multipath detection using a machine learning approach. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–6. [Google Scholar]
- Dodson, A.; Meng, X.; Roberts, G. Adaptive method for multipath mitigation and its applications for structural deflection monitoring. In Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation (KIS 2001), Banff, AB, Canada, 5–8 June 2001; pp. 101–110. [Google Scholar]
- Gao, W.; Meng, X.; Gao, C.; Pan, S.; Zhu, Z.; Xia, Y. Analysis of the carrier-phase multipath in GNSS triple-frequency observation combinations. Adv. Space Res. 2019, 63, 2735–2744. [Google Scholar] [CrossRef]
- Mubarak, O.M.; Dempster, A.G. Analysis of early late phase in single-and dual-frequency gps receivers for multipath detection. GPS Solut. 2010, 14, 381–388. [Google Scholar] [CrossRef]
- Miceli, R.J.; Psiaki, M.L.; O’Hanlon, B.W.; Chiang, K.Q. Real-time multipath estimation for dual frequency GPS ionospheric delay measurements. In Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 20–23 September 2011; pp. 1173–1178. [Google Scholar]
- Wu, X.L.; Zhou, J.H.; Gang, W.; Hu, X.G.; Cao, Y.L. Multipath error detection and correction for GEO/IGSO satellites. Sci. China Phys. Mech. Astron. 2012, 55, 1297–1306. [Google Scholar] [CrossRef]
- Rudi, M. GNSS Multipath Detection and Mitigation from Multiple-Frequency Measurements. Master’s Thesis, University College London, London, UK, 2012. [Google Scholar]
- Groves, P.D.; Jiang, Z.; Rudi, M.; Strode, P. A Portfolio Approach to NLOS and Multipath Mitigation in Dense Urban Areas. In Proceedings of the 26th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2013), Nashville Convention Center, Nashville, TN, USA, 16–20 September 2013; pp. 3231–3247. [Google Scholar]
- Ollander, S.; Bode, F.W.; Baum, M. Multi-frequency GNSS signal fusion for minimization of multipath and non-line-of-sight errors: A survey. In Proceedings of the 15th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 25–26 October 2018; pp. 1–6. [Google Scholar]
- Hannah, B.M. Modelling and Simulation of GPS Multipath Propagation. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, March 2001. [Google Scholar]
- Strode, P.R.R.; Groves, P.D. GNSS Multipath Detection using Three-frequency Signal-to-noise Measurements. GPS Solut. 2016, 20, 399–412. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Li, B.; Gao, Y.; Shen, Y. Real-time carrier phase multipath detection based on dual-frequency C/N0 data. GPS Solut. 2018, 23, 7. [Google Scholar] [CrossRef]
- Špánik, P.; García-Asenjo, L.; Baselga, S. Optimal combination and reference functions of signal-to-noise measurements for GNSS multipath detection. Meas. Sci. Technol. 2019, 30, 044001. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, UK, 1977. [Google Scholar]
- Kimber, A.C. Exploratory data analysis for possibly censored data from skewed distributions. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1990, 39, 21–30. [Google Scholar] [CrossRef]
- Aucremanne, L.; Brys, G.; Hubert, M.; Rousseeuw, P.J.; Struyf, A. A Study of Belgian Inflation, Relative Prices and Nominal Rigidities using New Robust Measures of Skewness and Tail Weight. In Theory and Applications of Recent Robust Methods; Hubert, M., Pison, G., Struyf, A., Van Aelst, S., Eds.; Birkhäuser Verlag: Basel, Switzerland, 2004; pp. 13–25. [Google Scholar]
- Carling, K. Resistant outlier rules and the non-gaussian case. Comput. Stat. Data Anal. 2000, 33, 249–258. [Google Scholar] [CrossRef] [Green Version]
- Schwertman, N.C.; Owens, M.A.; Adnan, R. A simple more general boxplot method for identifying outliers. Comput. Stat. Data Anal. 2004, 47, 165–174. [Google Scholar] [CrossRef]
- Schwertman, N.C.; de Silva, R. Identifying outliers with sequential fences. Comput. Stat. Data Anal. 2007, 51, 3800–3810. [Google Scholar] [CrossRef]
- Hubert, M.; Vandervieren, E. An adjusted boxplot for skewed distributions. Comput. Stat. Data Anal. 2008, 52, 5186–5201. [Google Scholar] [CrossRef]
- Bloomfield, P.; Steiger, W.L. Least Absolute Deviations: Theory, Applications, and Algorithms; Birkhäuser: Boston, MA, USA, 1983. [Google Scholar]
- Koenker, R.; Bassett, G. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K.F. Quantile regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Estey, L.; Meertens, C.M. TEQC: The multi-purpose toolkit for GPS/GLONASS Data. GPS Solut. 1999, 3, 42–49. [Google Scholar] [CrossRef]
- Hilla, S.; Cline, M. Evaluating pseudorange multipath effects at stations in the national CORS network. GPS Solut. 2004, 7, 253–267. [Google Scholar] [CrossRef]
- Holland, P.W.; Welsch, R.E. Robust regression using iteratively reweighted least-squares. Commun. Stat. Theory 1977, 6, 813–827. [Google Scholar] [CrossRef]
- Burrus, C.S. Iterative Reweighted Least Squares. OpenStax CNX. Available online: http://cnx.org/contents/92b90377-2b34-49e4-b26f-7fe572db78a1 (accessed on 12 December 2012).
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Brys, G.; Hubert, M.; Struyf, A. A robust measure of skewness. J. Comput. Graph. Stat. 2004, 13, 996–1018. [Google Scholar] [CrossRef]
- Choi, K.; Bilich, A.; Larson, K.M.; Axelrad, P. Modified sidereal filtering: Implications for high-rate GPS positioning. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Fuhrmann, T.; Luo, X.; Knopfler, A.; Mayer, M. Generating statistically robust multipath stacking maps using congruent cells. GPS Solut. 2015, 19, 83–92. [Google Scholar] [CrossRef]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Meguro, J.; Murata, T.; Takiguchi, J.; Amano, Y.; Hashizume, T. GPS multipath mitigation for urban area using omnidirectional infrared camera. IEEE Trans. Intell. Transp. Syst. 2009, 10, 22–30. [Google Scholar] [CrossRef]
- Hsu, L.T.; Gu, Y.; Kamijo, S. NLOS correction/exclusion for GNSS measurement using RAIM and city building models. Sensors 2015, 7, 17329–17349. [Google Scholar] [CrossRef] [Green Version]
- Wen, W.; Zhang, G.; Hsu, L.-T. GNSS NLOS Exclusion Based on Dynamic Object Detection Using LiDAR Point Cloud. IEEE Trans. Intell. Transp. Syst. 2019, 1–10. [Google Scholar] [CrossRef]
- Quan, Y.; Lau, L.; Roberts, G.W.; Meng, X.; Zhang, C. Convolutional Neural Network Based Multipath Detection Method for Static and Kinematic GPS High Precision Positioning. Remote Sens. 2018, 10, 2052. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Jia, Q.; Luo, Y.; Hsu, L.-T. Intelligent GPS L1 LOS/Multipath/NLOS Classifiers Based on Correlator-, RINEX- and NMEA-Level Measurements. Remote Sens. 2019, 11, 1851. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.; Hsu, L.-T.; Xue, D.; Zhang, G.; Ochieng, W.Y. GPS signal reception classification using adaptive neuro-fuzzy inference system. J. Navig. 2019, 72, 685–701. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Pan, S.; Meng, X.; Gao, W.; Ye, F.; Zhao, Q.; Zhao, X. Anomaly Detection for Urban Vehicle GNSS Observation with a Hybrid Machine Learning System. Remote Sens. 2020, 12, 971. [Google Scholar] [CrossRef] [Green Version]
- Ziedan, N. Urban positioning accuracy enhancement utilizing 3D buildings model and accelerated ray tracing algorithm. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 25–29 September 2017; pp. 3253–3268. [Google Scholar]
- Yozevitch, R.; Moshe, B.B.; Weissman, A. A robust GNSS LOS NLOS signal classifier. Navigation 2016, 63, 429–442. [Google Scholar] [CrossRef]






















| Elevation Range (°) | Sample Size | Skewness | Kurtosis | Mean (dB-Hz) | Median (dB-Hz) | Kolmogorov–Smirnov Test Statistics |
|---|---|---|---|---|---|---|
| 10~11 | 4356 | 1.302 | 0.979 | 2.745 | 2.017 | 0.690 |
| 20~21 | 7576 | 1.207 | 1.619 | 1.762 | 1.517 | 0.595 |
| 30~31 | 4599 | 0.944 | 1.012 | 1.667 | 1.573 | 0.597 |
| 40~41 | 3519 | −0.043 | −0.565 | 1.511 | 1.540 | 0.638 |
| 50~51 | 5720 | 0.262 | −0.238 | 1.509 | 1.546 | 0.588 |
| 60~61 | 2428 | 0.630 | −0.247 | 1.384 | 1.219 | 0.566 |
| 70~71 | 2269 | 1.377 | 1.734 | 1.317 | 1.047 | 0.564 |
| 80~81 | 882 | 1.410 | 2.517 | 0.837 | 0.724 | 0.539 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Pan, S.; Meng, X.; Gao, W.; Wen, H. Robust Statistical Detection of GNSS Multipath Using Inter-Frequency C/N0 Differences. Remote Sens. 2020, 12, 3388. https://doi.org/10.3390/rs12203388
Xia Y, Pan S, Meng X, Gao W, Wen H. Robust Statistical Detection of GNSS Multipath Using Inter-Frequency C/N0 Differences. Remote Sensing. 2020; 12(20):3388. https://doi.org/10.3390/rs12203388
Chicago/Turabian StyleXia, Yan, Shuguo Pan, Xiaolin Meng, Wang Gao, and He Wen. 2020. "Robust Statistical Detection of GNSS Multipath Using Inter-Frequency C/N0 Differences" Remote Sensing 12, no. 20: 3388. https://doi.org/10.3390/rs12203388
APA StyleXia, Y., Pan, S., Meng, X., Gao, W., & Wen, H. (2020). Robust Statistical Detection of GNSS Multipath Using Inter-Frequency C/N0 Differences. Remote Sensing, 12(20), 3388. https://doi.org/10.3390/rs12203388