Evaluation of the MODIS LAI/FPAR Algorithm Based on 3D-RTM Simulations: A Case Study of Grassland
Abstract
:1. Introduction
2. Materials and Methods
2.1. MODIS LAI/FPAR Retrieval Algorithm
2.2. Three-Dimensional Grassland Scene Simulation
2.3. Experimental Design
3. Results
3.1. Inherent Model Uncertainty
3.1.1. Analysis of Retrieval Space
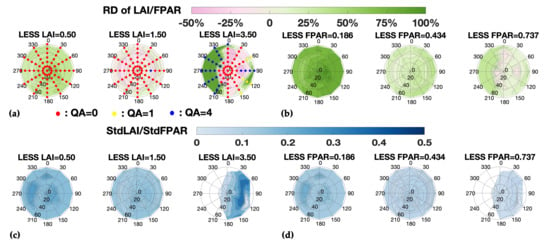
3.1.2. Retrieval Uncertainty as a Function of Sun–Sensor Geometry
3.2. Input BRF Uncertainty
3.3. Input Biome Type Uncertainty
3.4. Impact of Clumping Effect and Scale Dependency
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jacquemoud, S.; Baret, F.; Hanocq, J. Modeling spectral and bidirectional soil reflectance. Remote Sens. Environ. 1992, 41, 123–132. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- GCOS. Systematic observation requirements for satellite-based products for climate. 2011 update supplemetnatl details to the satellite 39 based component og the implementation plan for the global observing system for climate in support of the unfccc (2010 update). In Technical Report; World Meteorological Organisation (WMO): Geneva, Switzerland, 2011. [Google Scholar]
- Knyazikhin, Y.; Martonchik, J.; Myneni, R.B.; Diner, D.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef] [Green Version]
- Sellers, P.; Dickinson, R.E.; Randall, D.; Betts, A.; Hall, F.; Berry, J.; Collatz, G.; Denning, A.; Mooney, H.; Nobre, C. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global data sets of vegetation leaf area index (LAI) 3g and fraction of photosynthetically active radiation (FPAR) 3g derived from global inventory modeling and mapping studies (GIMMS) normalized difference vegetation index (NDVI3g) for the period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar]
- Mason, P.; Zillman, J.; Simmons, A.; Lindstrom, E.; Harrison, D.; Dolman, H.; Bojinski, S.; Fischer, A.; Latham, J.; Rasmussen, J. Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC (2010 Update); World Meteorological Organization: Geneva, Switzerland, 2010; p. 180. [Google Scholar]
- Knyazikhin, Y. MODIS Leaf Area Index (LAI) and Fraction of Photosynthetically Active Radiation Absorbed by Vegetation (FPAR) Product (MOD 15) Algorithm Theoretical Basis Document. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod15.pdf (accessed on 2 February 2017).
- Yan, K.; Park, T.; Yan, G.; Chen, C.; Yang, B.; Liu, Z.; Nemani, R.; Knyazikhin, Y.; Myneni, R. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements. Remote Sens. 2016, 8, 359. [Google Scholar] [CrossRef] [Green Version]
- Myneni, R.; Park, Y. MODIS Collection 6 (C6) LAI/FPAR Product User’s Guide. Available online: https://lpdaac.usgs.gov/sites/default/files/public/product_documentation/mod15_user_guide.pdf (accessed on 1 January 2016).
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Dirmeyer, P.A. Adapting observationally based metrics of biogeophysical feedbacks from land cover/land use change to climate modeling. Environ. Res. Lett. 2016, 11, 034002. [Google Scholar] [CrossRef] [Green Version]
- Kala, J.; Decker, M.; Exbrayat, J.-F.; Pitman, A.J.; Carouge, C.; Evans, J.P.; Abramowitz, G.; Mocko, D. Influence of leaf area index prescriptions on simulations of heat, moisture, and carbon fluxes. J. Hydrometeorol. 2014, 15, 489–503. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Park, T.; Wang, X.; Piao, S.; Xu, B.; Chaturvedi, R.K.; Fuchs, R.; Brovkin, V.; Ciais, P.; Fensholt, R.; et al. China and India lead in greening of the world through land-use management. Nat. Sustain. 2019, 2, 122–129. [Google Scholar] [CrossRef]
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, C.; Band, L.E.; Sun, G.; Li, J. Reanalysis of global terrestrial vegetation trends from MODIS products: Browning or greening? Remote Sens. Environ. 2017, 191, 145–155. [Google Scholar] [CrossRef] [Green Version]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmara, H.; Pacholcyzk, P.; Smets, B. GEOV1: LAI and FAPAR essential climate variables and FCOVER global time series capitalizing over existing products. Part1: Principles of development and production. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product From Time-Series MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Baret, F.; Buis, S. Estimating canopy characteristics from remote sensing observations: Review of methods and associated problems. In Advances in Land Remote Sensing; Springer: Berlin/Heidelberg, Germany, 2008; pp. 173–201. [Google Scholar]
- Claverie, M.; Vermote, E.F.; Weiss, M.; Baret, F.; Hagolle, O.; Demarez, V. Validation of coarse spatial resolution LAI and FAPAR time series over cropland in southwest France. Remote Sens. Environ. 2013, 139, 216–230. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Chen, C.; Xu, B.; Song, W.; Yang, B.; Zeng, Y.; Liu, Z.; Yan, G.; Knyazikhin, Y.J.I.T.o.G.; et al. Generating global products of lai and fpar from snpp-viirs data: Theoretical background and implementation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2119–2137. [Google Scholar] [CrossRef]
- Serbin, S.P.; Ahl, D.E.; Gower, S.T. Spatial and temporal validation of the MODIS LAI and FPAR products across a boreal forest wildfire chronosequence. Remote Sens. Environ. 2013, 133, 71–84. [Google Scholar] [CrossRef]
- Fuster, B.; Sánchez-Zapero, J.; Camacho, F.; García-Santos, V.; Verger, A.; Lacaze, R.; Weiss, M.; Baret, F.; Smets, B. Quality Assessment of PROBA-V LAI, fAPAR and fCOVER Collection 300 m Products of Copernicus Global Land Service. Remote Sens. 2020, 12, 1017. [Google Scholar] [CrossRef] [Green Version]
- Weiss, M.; Baret, F.; Block, T.; Koetz, B.; Burini, A.; Scholze, B.; Lecharpentier, P.; Brockmann, C.; Fernandes, R.; Plummer, S. On Line Validation Exercise (OLIVE): A web based service for the validation of medium resolution land products. Application to FAPAR products. Remote Sens. 2014, 6, 4190–4216. [Google Scholar] [CrossRef] [Green Version]
- Yan, K.; Park, T.; Yan, G.; Liu, Z.; Yang, B.; Chen, C.; Nemani, R.; Knyazikhin, Y.; Myneni, R. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 2: Validation and Intercomparison. Remote Sens. 2016, 8, 460. [Google Scholar] [CrossRef] [Green Version]
- De Kauwe, M.G.; Disney, M.; Quaife, T.; Lewis, P.; Williams, M. An assessment of the MODIS collection 5 leaf area index product for a region of mixed coniferous forest. Remote Sens. Environ. 2011, 115, 767–780. [Google Scholar] [CrossRef]
- Loew, A.; Bell, W.; Brocca, L.; Bulgin, C.E.; Burdanowitz, J.; Calbet, X.; Donner, R.V.; Ghent, D.; Gruber, A.; Kaminski, T. Validation practices for satellite based earth observation data across communities. Rev. Geophys. 2017, 55, 779–817. [Google Scholar] [CrossRef] [Green Version]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An overview of global leaf area index (LAI): Methods, products, validation, and applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Fang, H.; Wei, S.; Liang, S. Validation of MODIS and CYCLOPES LAI products using global field measurement data. Remote Sens. Environ. 2012, 119, 43–54. [Google Scholar] [CrossRef]
- Somers, B.; Tits, L.; Coppin, P. Quantifying Nonlinear Spectral Mixing in Vegetated Areas: Computer Simulation Model Validation and First Results. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1956–1965. [Google Scholar] [CrossRef]
- Schneider, F.D.; Leiterer, R.; Morsdorf, F.; Gastelluetchegorry, J.P.; Lauret, N.; Pfeifer, N.; Schaepman, M.E. Simulating imaging spectrometer data: 3D forest modeling based on LiDAR and in situ data. Remote Sens. Environ. 2014, 152, 235–250. [Google Scholar] [CrossRef]
- Lanconelli, C.; Gobron, N.; Adams, J.; Danne, O.; Blessing, S.; Robustelli, M.; Kharbouche, S.; Muller, J. Report on the Quality Assessment of Land ECV Retrieval Algorithms; Scientific and Technical Report JRC109764; European Commission, Joint Research Centre: Ispra, Italy, 2018. [Google Scholar]
- Gastellu-Etchegorry, J.-P.; Yin, T.; Lauret, N.; Cajgfinger, T.; Gregoire, T.; Grau, E.; Feret, J.-B.; Lopes, M.; Guilleux, J.; Dedieu, G. Discrete anisotropic radiative transfer (DART 5) for modeling airborne and satellite spectroradiometer and LIDAR acquisitions of natural and urban landscapes. Remote Sens. 2015, 7, 1667–1701. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Qin, W.; Liu, Q. RAPID: A Radiosity Applicable to Porous IndiviDual Objects for directional reflectance over complex vegetated scenes. Remote Sens. Environ. 2013, 132, 221–237. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Yin, T.; Yan, G.; Gastellu-Etchegorry, J.-P.; Li, L.; Zhang, W.; Mu, X.; Norford, L.K. LESS: LargE-Scale remote sensing data and image simulation framework over heterogeneous 3D scenes. Remote Sens. Environ. 2019, 221, 695–706. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Pinty, B.; Lopatka, M.; Atzberger, C.; Buzica, D.; Chelle, M.; Disney, M.; Gastelluetchegorry, J.; Gerboles, M.; Gobron, N. The fourth radiation transfer model intercomparison (RAMI-IV): Proficiency testing of canopy reflectance models with ISO-13528. J. Geophys. Res. 2013, 118, 6869–6890. [Google Scholar] [CrossRef] [Green Version]
- Disney, M.; Lewis, P.; Saich, P. 3D modelling of forest canopy structure for remote sensing simulations in the optical and microwave domains. Remote Sens. Environ. 2006, 100, 114–132. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Côté, J.-F.; Béland, M. Abstract tree crowns in 3D radiative transfer models: Impact on simulated open-canopy reflectances. Remote Sens. Environ. 2014, 142, 155–175. [Google Scholar] [CrossRef]
- Kuusk, A. 3.03—Canopy Radiative Transfer Modeling. In Comprehensive Remote Sensing; Liang, S., Ed.; Elsevier: Oxford, UK, 2018; pp. 9–22. [Google Scholar] [CrossRef]
- Gastelluetchegorry, J.P.; Martin, E.; Gascon, F. DART: A 3D model for simulating satellite images and studying surface radiation budget. Int. J. Remote Sens. 2004, 25, 73–96. [Google Scholar] [CrossRef]
- Bruniquelpinel, V.; Gastelluetchegorry, J.P. Sensitivity of Texture of High Resolution Images of Forest to Biophysical and Acquisition Parameters. Remote Sens. Environ. 1998, 65, 61–85. [Google Scholar] [CrossRef]
- Guillevic, P.; Gastellu-Etchegorry, J. Modeling BRF and radiative regime of tropical and boreal forests—PART II: PAR regime. Remote Sens. Environ. 1999, 68, 317–340. [Google Scholar] [CrossRef]
- Demarez, V.; Gastelluetchegorry, J.P. A Modeling Approach for Studying Forest Chlorophyll Content. Remote Sens. Environ. 2000, 71, 226–238. [Google Scholar] [CrossRef]
- Malenovsky, Z.; Homolova, L.; Zuritamilla, R.; Lukes, P.; Kaplan, V.; Hanus, J.; Gastelluetchegorry, J.P.; Schaepman, M.E. Retrieval of spruce leaf chlorophyll content from airborne image data using continuum removal and radiative transfer. Remote Sens. Environ. 2013, 131, 85–102. [Google Scholar] [CrossRef] [Green Version]
- Qi, J.; Xie, D.; Yan, G.; Gastelluetchegorry, J.P. Simulating Spectral Images with Less Model Through a Voxel-Based Parameterization of Airborne Lidar Data. In Proceedings of the International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 6043–6046. [Google Scholar]
- Qi, J.; Xie, D.; Guo, D.; Yan, G. A Large-Scale Emulation System for Realistic Three-Dimensional (3-D) Forest Simulation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 4834–4843. [Google Scholar] [CrossRef]
- Huang, D.; Knyazikhin, Y.; Wang, W.; Deering, D.W.; Stenberg, P.; Shabanov, N.V.; Tan, B.; Myneni, R.B. Stochastic transport theory for investigating the three-dimensional canopy structure from space measurements. Remote Sens. Environ. 2008, 112, 35–50. [Google Scholar] [CrossRef]
- Yang, B.; Knyazikhin, Y.; Mottus, M.; Rautiainen, M.; Stenberg, P.; Yan, L.; Chen, C.; Yan, K.; Choi, S.; Park, T. Estimation of leaf area index and its sunlit portion from DSCOVR EPIC data: Theoretical basis. Remote Sens. Environ. 2017, 198, 69–84. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Tan, B.; Huang, D.; Rautiainen, M.; Shabanov, N.V.; Wang, Y.; Privette, J.L.; Huemmrich, K.F.; Fensholt, R.; Sandholt, I. MODIS leaf area index products: From validation to algorithm improvement. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1885–1898. [Google Scholar] [CrossRef]
- Hosgood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf optical properties experiment 93 (LOPEX93). Rep. Eur. 1995, 16095. [Google Scholar]
- Trigg, S.; Flasse, S. Characterizing the spectral-temporal response of burned savannah using in situ spectroradiometry and infrared thermometry. Int. J. Remote Sens. 2000, 21, 3161–3168. [Google Scholar] [CrossRef]
- Fang, H.; Jiang, C.; Li, W.; Wei, S.; Baret, F.; Chen, J.M.; Garcia-Haro, J.; Liang, S.; Liu, R.; Myneni, R.B.; et al. Characterization and intercomparison of global moderate resolution leaf area index (LAI) products: Analysis of climatologies and theoretical uncertainties. J. Geophys. Res. 2013, 118, 529–548. [Google Scholar] [CrossRef]
- Xu, B.; Park, T.; Yan, K.; Chen, C.; Zeng, Y.; Song, W.; Yin, G.; Li, J.; Liu, Q.; Knyazikhin, Y.; et al. Analysis of Global LAI/FPAR Products from VIIRS and MODIS Sensors for Spatio-Temporal Consistency and Uncertainty from 2012–2016. Forests 2018, 9, 73. [Google Scholar] [CrossRef] [Green Version]
- Knyazikhin, Y.; Martonchik, J.V.; Diner, D.J.; Myneni, R.B.; Verstraete, M.M.; Pinty, B.; Gobron, N. Estimation of vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from atmosphere-corrected MISR data. J. Geophys. Res. 1998, 103, 32239–32256. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Kuusk, A. The hot spot effect on a uniform vegetative cover. Sov. J. Remote Sens 1985, 3, 645–658. [Google Scholar]
- Roujean, J.-L. A parametric hot spot model for optical remote sensing applications. Remote Sens. Environ. 2000, 71, 197–206. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.R.; Running, S.W. Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef] [Green Version]









| R (Red) | T (Red) | R (NIR) | T (NIR) | |
|---|---|---|---|---|
| Johnson grass | 0.0738 | 0.0577 | 0.4276 | 0.4607 |
| Grayish brown loam | 0.1755 | 0 | 0.3021 | 0 |
| Experiment | LAI | SZA | SAA | VZA | VAA | Uncertainty Metrics |
|---|---|---|---|---|---|---|
| Retrieval Space | / | 0° | 0° | 0° | 0° | StdLAI, StdFPAR |
| Sun–Sensor Geometry | 0.50, 1.5, 3.5 | 30°/ 0°:10°:60° | 90°/ 0°:30°:330° | 0°:10°:60°/30° | 0°:30°:330°/ 90° | RD, StdLAI, StdFPAR |
| BRF Uncertainty | 1.5 | 0° | 0° | −60°:10°:60° | 0° | RD, StdLAI, StdFPAR |
| Biome Type Uncertainty | 0.25, 0.50, 0.75, 1.0, 1.25, 1.5, 2.5, 3.5, 4.5 | 0° | 0° | 0°:10°:60° | 0°:30°:330° | RI, AD |
| Clumping and Scale Effect | 1.5 | 30° | 0° | 0°:30°:60° | 0°:60°:300° | RI, StdLAI, StdFPAR |
| Scene | 100 m | 250 m | 500 m | 1000 m | |
|---|---|---|---|---|---|
| RI (N. of main/N. of all) | Uniform | 1700/1800 | 272/288 | 68/72 | 17/18 |
| CT1 | 1743/1800 | 279/288 | 70/72 | 18/18 | |
| CT2 | 1565/1800 | 251/288 | 62/72 | 17/18 | |
| StdLAI (mean ± Std) | Uniform | 0.147± 0.019 | 0.148± 0.019 | 0.149± 0.020 | 0.150± 0.021 |
| CT1 | 0.251± 0.108 | 0.218± 0.074 | 0.225± 0.066 | 0.179± 0.074 | |
| CT2 | 0.340± 0.160 | 0.339± 0.160 | 0.342± 0.159 | 0.181± 0.027 | |
| StdFPAR (mean ± Std) | Uniform | 0.088± 0.012 | 0.088± 0.012 | 0.089± 0.012 | 0.089± 0.013 |
| CT1 | 0.208± 0.109 | 0.177± 0.070 | 0.180± 0.058 | 0.144± 0.061 | |
| CT2 | 0.269± 0.188 | 0.269± 0.188 | 0.271± 0.187 | 0.130± 0.022 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, J.; Yan, K.; Zhou, G.; Lei, Y.; Zhu, Y.; Guo, D.; Li, H.; Xu, L.; Knyazikhin, Y.; Myneni, R.B. Evaluation of the MODIS LAI/FPAR Algorithm Based on 3D-RTM Simulations: A Case Study of Grassland. Remote Sens. 2020, 12, 3391. https://doi.org/10.3390/rs12203391
Pu J, Yan K, Zhou G, Lei Y, Zhu Y, Guo D, Li H, Xu L, Knyazikhin Y, Myneni RB. Evaluation of the MODIS LAI/FPAR Algorithm Based on 3D-RTM Simulations: A Case Study of Grassland. Remote Sensing. 2020; 12(20):3391. https://doi.org/10.3390/rs12203391
Chicago/Turabian StylePu, Jiabin, Kai Yan, Guohuan Zhou, Yongqiao Lei, Yingxin Zhu, Donghou Guo, Hanliang Li, Linlin Xu, Yuri Knyazikhin, and Ranga B. Myneni. 2020. "Evaluation of the MODIS LAI/FPAR Algorithm Based on 3D-RTM Simulations: A Case Study of Grassland" Remote Sensing 12, no. 20: 3391. https://doi.org/10.3390/rs12203391
APA StylePu, J., Yan, K., Zhou, G., Lei, Y., Zhu, Y., Guo, D., Li, H., Xu, L., Knyazikhin, Y., & Myneni, R. B. (2020). Evaluation of the MODIS LAI/FPAR Algorithm Based on 3D-RTM Simulations: A Case Study of Grassland. Remote Sensing, 12(20), 3391. https://doi.org/10.3390/rs12203391