Ocean Surface Topography Altimetry by Large Baseline Cross-Interferometry from Satellite Formation
Abstract
:1. Introduction
2. Measurement Principle
2.1. Altimetry Principle
2.2. Relative Altimetric Accuracy
3. Satellite Formation and Interferometry Baseline
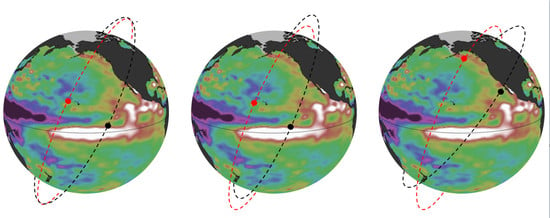
3.1. Helix Orbit Configuration
3.2. Along-Track Baseline and Time Decorrelation
3.3. Baseline Variation Cycle
4. CFS for Baseline Decorrelation Compensation
4.1. Principle of Baseline Decorrelation
4.2. Design Princile of CFS
4.2.1. Radar Look Angle
4.2.2. Cross-Track Baseline Length
4.2.3. Ocean Surface Slope
5. Methodology for Altimetric Accuracy Analysis
5.1. Parameters Setting
5.2. Multi-Looking
6. Numerical Results of LB-IRA
7. Conclusions
- The CFS method can release the baseline length limitation from baseline decorrelation, also increasing the freedom of selecting other interferometric parameters.
- The altimetric error associated to phase noise is only a few millimeters, which is quite extraordinary owing to much larger baseline length than that of the single platform.
- It poses relatively easier or fewer technical or engineering challenges, such as the rigorous attitude control accuracy, or the mast vibration or dilation error that should be addressed by the SWOT team.
- The relative altimetric accuracy is quite consistent throughout the entire swath, facilitating marine application based on the OST gradient.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fu, L.-L.; Chelton, D.B.; Le Traon, P.-Y.; Morrow, R. Eddy dynamics from satellite altimetry. Oceanography 2010, 23, 14–25. [Google Scholar] [CrossRef] [Green Version]
- Sandwell, D.T.; Smith, W.H. Marine gravity anomaly from Geosat and ERS 1 satellite altimetry. J. Geophys. Res. Solid Earth 1997, 102, 10039–10054. [Google Scholar] [CrossRef] [Green Version]
- Chelton, D.B.; Ries, J.C.; Haines, B.J.; Fu, L.-L.; Callahan, P.S. Satellite altimetry. In International Geophysics; Elsevier: Amsterdam, The Netherlands, 2001; Volume 69, pp. 1–2. [Google Scholar]
- Scharroo, R.; Bonekamp, H.; Ponsard, C.; Parisot, F.; von Engeln, A.; Tahtadjiev, M.; de Vriendt, K.; Montagner, F. Jason continuity of services: Continuing the Jason altimeter data records as Copernicus Sentinel-6. Ocean Sci. 2016, 12, 471–479. [Google Scholar] [CrossRef] [Green Version]
- Quartly, G.D.; Legeais, J.-F.; Ablain, M.; Zawadzki, L.; Fernandes, M.J.; Rudenko, S.; Carrère, L.; García, P.N.; Cipollini, P.; Andersen, O.B. A new phase in the production of quality-controlled sea level data. Earth Syst. Sci. Data 2017, 9, 557–572. [Google Scholar] [CrossRef] [Green Version]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1. [Google Scholar] [CrossRef]
- Rodriguez, E.; Pollard, B.; Martin, J. Wide-swath ocean altimetry using radar interferometry. IEEE Trans. Geosci. Remote Sens. 1999. Available online: http://hdl.handle.net/2014/17962 (accessed on 23 September 2020).
- Fu, L.-L.; Ubelmann, C. On the transition from profile altimeter to swath altimeter for observing global ocean surface topography. J. Atmos. Ocean. Technol. 2014, 31, 560–568. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.-L.; Alsdorf, D.; Morrow, R.; Rodriguez, E.; Mognard, N. SWOT: The Surface Water and Ocean Topography Mission: Wide-Swath Altimetric Elevation on Earth; Jet Propulsion Laboratory, National Aeronautics and Space: Pasadena, CA, USA, 2012.
- Fu, L.-L.; Alsdorf, D.; Rodriguez, E.; Morrow, R.; Mognard, N.; Lambin, J.; Vaze, P.; Lafon, T. The SWOT (Surface Water and Ocean Topography) mission: Spaceborne radar interferometry for oceanographic and hydrological applications. In Proceedings of the OCEANOBS’09, Venice, Italy, 21–25 September 2009. [Google Scholar]
- Agnes, G.S.; Waldman, J.; Peterson, L.; Hughes, R. Testing the Deployment Repeatability of a Precision Deployable Boom Prototype for the Proposed SWOT KaRIn Instrument. In Proceedings of the 2nd AIAA Spacecraft Structures Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 1838. [Google Scholar]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Van Zyl, J.J. The Shuttle Radar Topography Mission (SRTM): A breakthrough in remote sensing of topography. Acta Astronaut. 2001, 48, 559–565. [Google Scholar] [CrossRef]
- Fjørtoft, R.; Gaudin, J.-M.; Pourthié, N.; Lalaurie, J.-C.; Mallet, A.; Nouvel, J.-F.; Martinot-Lagarde, J.; Oriot, H.; Borderies, P.; Ruiz, C. KaRIn on SWOT: Characteristics of near-nadir Ka-band interferometric SAR imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2172–2185. [Google Scholar] [CrossRef]
- Kong, W.; Chong, J.; Tan, H. Performance analysis of ocean surface topography altimetry by Ku-Band Near-Nadir interferometric SAR. Remote Sens. 2017, 9, 933. [Google Scholar] [CrossRef] [Green Version]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Hounam, D.; Werner, M.; Riegger, S.; Settelmeyer, E. TanDEM-X: A TerraSAR-X add-on satellite for single-pass SAR interferometry. In Proceedings of the IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; pp. 1000–1003. [Google Scholar]
- Gatelli, F.; Guamieri, A.M.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The wavenumber shift in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1994, 32, 855–865. [Google Scholar] [CrossRef] [Green Version]
- Wegmüller, U.; Santoro, M.; Werner, C.; Strozzi, T.; Wiesmann, A.; Lengert, W. DEM generation using ERS–ENVISAT interferometry. J. Appl. Geophys. 2009, 69, 51–58. [Google Scholar] [CrossRef]
- Arnaud, A.; Adam, N.; Hanssen, R.; Inglada, J.; Duro, J.; Closa, J.; Eineder, M. ASAR ERS interferometric phase continuity. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No. 03CH37477), Toulouse, France, 21–25 July 2003; pp. 1133–1135. [Google Scholar]
- Perissin, D.; Prati, C.; Engdahl, M.E.; Desnos, Y.-L. Validating the SAR wavenumber shift principle with the ERS–Envisat PS coherent combination. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2343–2351. [Google Scholar] [CrossRef]
- Santoro, M.; Askne, J.I.; Wegmuller, U.; Werner, C.L. Observations, modeling, and applications of ERS-ENVISAT coherence over land surfaces. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2600–2611. [Google Scholar] [CrossRef]
- Rodriguez, E.; Martin, J. Theory and design of interferometric synthetic aperture radars. In Proceedings of the IEE Proceedings F (Radar and Signal Processing); April 1992; pp. 147–159. Available online: https://digital-library.theiet.org/content/journals/10.1049/ip-f-2.1992.0018 (accessed on 26 October 2020).
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A satellite formation for high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef] [Green Version]
- Esteban-Fernandez, D. SWOT Project Mission Performance and Error Budget Document. JPL D-79084; 2014; pp. 41–43. Available online: https://pdms.jpl.nasa.gov/ (accessed on 23 September 2020).
- Reale, F.; Pugliese Carratelli, E.; Di Leo, A.; Dentale, F. Wave orbital velocity effects on radar Doppler altimeter for sea monitoring. J. Mar. Sci. Eng. 2020, 8, 447. [Google Scholar] [CrossRef]
- Suchandt, S.; Romeiser, R. X-band sea surface coherence time inferred from bistatic SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3941–3948. [Google Scholar] [CrossRef]
- Frasier, S.J.; Camps, A.J. Dual-beam interferometry for ocean surface current vector mapping. IEEE Trans. Geosci. Remote Sens. 2001, 39, 401–414. [Google Scholar] [CrossRef]
- Prati, C.; Rocca, F. Improving slant-range resolution with multiple SAR surveys. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 135–143. [Google Scholar] [CrossRef]
- Chua, M.Y.; Koo, V.C. FPGA-based chirp generator for high resolution UAV SAR. Prog. Electromagn. Res. 2009, 99, 71–88. [Google Scholar] [CrossRef] [Green Version]
- Nouguier, F.; Mouche, A.; Rascle, N.; Chapron, B.; Vandemark, D. Analysis of dual-frequency ocean backscatter measurements at Ku-and Ka-bands using near-nadir incidence GPM radar data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1310–1314. [Google Scholar] [CrossRef] [Green Version]
- Alberga, V. Volume decorrelation effects in polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2467–2478. [Google Scholar] [CrossRef]
- Peral, E.; Rodríguez, E.; Esteban-Fernández, D. Impact of surface waves on SWOT’s projected ocean accuracy. Remote Sens. 2015, 7, 14509–14529. [Google Scholar] [CrossRef] [Green Version]
- Dibarboure, G.; Labroue, S.; Ablain, M.; Fjortoft, R.; Mallet, A.; Lambin, J.; Souyris, J.-C. Empirical cross-calibration of coherent SWOT errors using external references and the altimetry constellation. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2325–2344. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.W. Flight performance analysis of GRACE K-band ranging instrument with simulation data. Acta Astronaut. 2009, 65, 1571–1581. [Google Scholar] [CrossRef]



















| Parameter | Value |
|---|---|
| Altitude | 891 km |
| Carrier frequency of Sat1 | 13.5 GHz |
| Carrier frequency of Sat2 | 13.5~13.6 GHz |
| CFS | 30~60 MHz |
| Bandwidth | 30~60 MHz |
| Radar look angle | 12~15 |
| Peak transmit power | 3000 W |
| Pulse length | |
| Pulse repeat frequency | 4000 |
| Antenna length | 5 m |
| Antenna width | 0.4 m |
| Cross-track baseline length | 629~1000 m |
| Along-track baseline length | 0~40 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, W.; Liu, B.; Sui, X.; Zhang, R.; Sun, J. Ocean Surface Topography Altimetry by Large Baseline Cross-Interferometry from Satellite Formation. Remote Sens. 2020, 12, 3519. https://doi.org/10.3390/rs12213519
Kong W, Liu B, Sui X, Zhang R, Sun J. Ocean Surface Topography Altimetry by Large Baseline Cross-Interferometry from Satellite Formation. Remote Sensing. 2020; 12(21):3519. https://doi.org/10.3390/rs12213519
Chicago/Turabian StyleKong, Weiya, Bo Liu, Xiaohong Sui, Running Zhang, and Jinping Sun. 2020. "Ocean Surface Topography Altimetry by Large Baseline Cross-Interferometry from Satellite Formation" Remote Sensing 12, no. 21: 3519. https://doi.org/10.3390/rs12213519
APA StyleKong, W., Liu, B., Sui, X., Zhang, R., & Sun, J. (2020). Ocean Surface Topography Altimetry by Large Baseline Cross-Interferometry from Satellite Formation. Remote Sensing, 12(21), 3519. https://doi.org/10.3390/rs12213519