Cascaded Microwave Frequency Transfer over 300-km Fiber Link with Instability at the 10−18 Level
Abstract
:1. Introduction
2. Materials and Methods
2.1. Principle of Frequency Transfer System
2.2. Experimental Setup
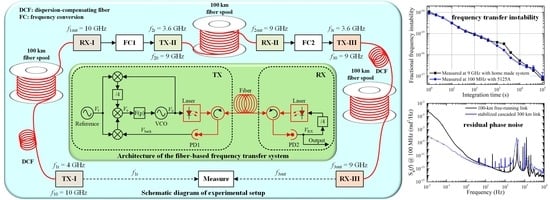
2.2.1. 10-GHz and 9-GHz Transfer Systems
2.2.2. Cascaded Microwave Frequency Transfer
2.2.3. Frequency Conversion for the Cascaded System
2.3. Phase Difference Measurement System
3. Results
3.1. The Single-Span Link
3.2. The Cascaded Link
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hachisu, H.; Fujieda, M.; Nagano, S.; Gotoh, T.; Nogami, A.; Ido, T.; Falke, S.; Huntemann, N.; Grebing, C.; Lipphardt, B.; et al. Direct comparison of optical lattice clocks with an intercontinental baseline of 9000 km. Opt. Lett. 2014, 39, 4072–4075. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riehle, F. Optical clock networks. Nat. Photonics 2017, 11, 25–31. [Google Scholar] [CrossRef]
- Shelkovnikov, A.; Butcher, R.J.; Chardonnet, C.; Amy-Klein, A. Stability of the proton-to-electron mass ratio. Phys. Rev. Lett. 2008, 100, 150801. [Google Scholar] [CrossRef] [Green Version]
- Matveev, A.; Parthey, C.G.; Predehl, K.; Alnis, J.; Beyer, A.; Holzwarth, R.; Udem, T.; Wilken, T.; Kolachevsky, N.; Abgrall, M.; et al. Precision measurement of the hydrogen 1S-2S frequency via a 920-km fiber link. Phys. Rev. Lett. 2013, 110, 230801. [Google Scholar] [CrossRef]
- Mehlstaubler, T.E.; Grosche, G.; Lisdat, C.; Schmidt, P.O.; Denker, H. Atomic clocks for geodesy. Rep. Prog. Phys. 2018, 81, 064401. [Google Scholar] [CrossRef] [Green Version]
- Cliche, J.F.; Shillue, B. Precision timing control for radioastronomy—Maintaining femtosecond synchronization in the atacama large millimeter array. IEEE Control Syst. Mag. 2006, 26, 19–26. [Google Scholar] [CrossRef]
- Schediwy, S.W.; Gozzard, D.R.; Gravestock, C.; Stobie, S.; Whitaker, R.; Malan, J.A.; Boven, P.; Grainge, K. The mid-frequency Square Kilometre Array phase synchronisation system. Publ. Astron. Soc. Aust. 2019, 36. [Google Scholar] [CrossRef] [Green Version]
- Gozzard, D.R.; Schediwy, S.W.; Dodson, R.; Rioja, M.J.; Hill, M.; Lennon, B.; McFee, J.; Mirtschin, P.; Stevens, J.; Grainge, K. Astronomical verification of a stabilized frequency reference transfer system for the Square Kilometer Array. Astron. J. 2017, 154. [Google Scholar] [CrossRef] [Green Version]
- Krehlik, P.; Buczek, Ł.; Kołodziej, J.; Lipiński, M.; Śliwczyński, Ł.; Nawrocki, J.; Nogaś, P.; Marecki, A.; Pazderski, E.; Ablewski, P.; et al. Fibre-optic delivery of time and frequency to VLBI station. Astron. Astrophys. 2017, 603, A48. [Google Scholar] [CrossRef]
- Clivati, C.; Aiello, R.; Bianco, G.; Bortolotti, C.; De Natale, P.; Di Sarno, V.; Maddaloni, P.; Maccaferri, G.; Mura, A.; Negusini, M.; et al. Common-clock very long baseline interferometry using a coherent optical fiber link. Optica 2020, 7, 1031–1037. [Google Scholar] [CrossRef]
- Lau, K.Y.; Lutes, G.F.; Tjoelker, R.L. Ultra-stable RF-over-fiber transport in NASA antennas, phased arrays and radars. J. Lightwave Technol. 2014, 32, 3440–3451. [Google Scholar] [CrossRef]
- Johnsen, T. Time and frequency synchronization in multistatic radar. Consequences to usage of GPS disciplined references with and without GPS signals. In Proceedings of the 2002 IEEE Radar Conference, Long Beach, CA, USA, 25 April 2002; pp. 141–147. [Google Scholar]
- Bauch, A.; Achkar, J.; Bize, S.; Calonico, D.; Dach, R.; Hlavać, R.; Lorini, L.; Parker, T.; Petit, G.; Piester, D.; et al. Comparison between frequency standards in Europe and the USA at the 10−15 uncertainty level. Metrologia 2006, 43, 109–120. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Kéfélian, F.; Crane, S.; Lopez, O.; Lours, M.; Millo, J.; Holleville, D.; Lemonde, P.; Chardonnet, C.; Amy-Klein, A.; et al. Long-distance frequency transfer over an urban fiber link using optical phase stabilization. J. Opt. Soc. Am. B 2008, 25, 2029–2035. [Google Scholar] [CrossRef] [Green Version]
- Bercy, A.; Stefani, F.; Lopez, O.; Chardonnet, C.; Pottie, P.-E.; Amy-Klein, A. Two-way optical frequency comparisons at 5×10−21 relative stability over 100-km telecommunication network fibers. Phys. Rev. A 2014, 90, 061802. [Google Scholar] [CrossRef] [Green Version]
- Deng, X.; Liu, J.; Jiao, D.D.; Gao, J.; Zang, Q.; Xu, G.J.; Dong, R.F.; Liu, T.; Zhang, S.G. Coherent transfer of optical frequency over 112 km with instability at the 10−20 level. Chin. Phys. Lett. 2016, 33, 114202. [Google Scholar] [CrossRef]
- Guillou-Camargo, F.; Menoret, V.; Cantin, E.; Lopez, O.; Quintin, N.; Camisard, E.; Salmon, V.; Le Merdy, J.M.; Santarelli, G.; Amy-Klein, A.; et al. First industrial-grade coherent fiber link for optical frequency standard dissemination. Appl. Opt. 2018, 57, 7203–7210. [Google Scholar] [CrossRef]
- Daussy, C.; Lopez, O.; Amy-Klein, A.; Goncharov, A.; Guinet, M.; Chardonnet, C.; Narbonneau, F.; Lours, M.; Chambon, D.; Bize, S.; et al. Long-distance frequency dissemination with a resolution of 10−17. Phys. Rev. Lett. 2005, 94, 203904. [Google Scholar] [CrossRef] [Green Version]
- Lopez, O.; Amy-Klein, A.; Lours, M.; Chardonnet, C.; Santarelli, G. High-resolution microwave frequency dissemination on an 86-km urban optical link. Appl. Phys. B 2009, 98, 723–727. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Gao, C.; Chen, W.L.; Miao, J.; Zhu, X.; Bai, Y.; Zhang, J.W.; Feng, Y.Y.; Li, T.C.; Wang, L.J. Precise and continuous time and frequency synchronisation at the 5 × 10−19 accuracy level. Sci. Rep. 2012, 2, 556. [Google Scholar] [CrossRef] [PubMed]
- Sliwczynski, L.; Krehlik, P.; Buczek, L.; Lipinski, M. Frequency transfer in electronically stabilized fiber optic link exploiting bidirectional optical amplifiers. IEEE Trans. Instrum. Meas. 2012, 61, 2573–2580. [Google Scholar] [CrossRef]
- Wang, S.; Sun, D.; Dong, Y.; Xie, W.; Shi, H.; Yi, L.; Hu, W. Distribution of high-stability 10 GHz local oscillator over 100 km optical fiber with accurate phase-correction system. Opt. Lett. 2014, 39, 888–891. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Wu, G.; Li, H.; Chen, J. Fiber-optic radio frequency transfer based on passive phase noise compensation with frequency dividing and filtering. Opt. Lett. 2016, 41, 626–629. [Google Scholar] [CrossRef]
- Schediwy, S.W.; Gozzard, D.R.; Stobie, S.; Malan, J.A.; Grainge, K. Stabilized microwave-frequency transfer using optical phase sensing and actuation. Opt. Lett. 2017, 42, 1648–1651. [Google Scholar] [CrossRef]
- Xue, W.X.; Zhao, W.Y.; Quan, H.L.; Zhao, C.C.; Xing, Y.; Jiang, H.F.; Zhang, S.G. Microwave frequency transfer over a 112-km urban fiber link based on electronic phase compensation. Chin. Phys. B 2020, 29, 064209. [Google Scholar] [CrossRef]
- Krehlik, P.; Sliwczynski, L.; Buczek, L.; Lipinski, M. Fiber-optic joint time and frequency transfer with active stabilization of the propagation delay. IEEE Trans. Instrum. Meas. 2012, 61, 2844–2851. [Google Scholar] [CrossRef]
- Sliwczynski, L.; Krehlik, P.; Czubla, A.; Buczek, L.; Lipinski, M. Dissemination of time and RF frequency via a stabilized fibre optic link over a distance of 420 km. Metrologia 2013, 50, 133–145. [Google Scholar] [CrossRef]
- Newbury, N.R.; Williams, P.A.; Swann, W.C. Coherent transfer of an optical carrier over 251 km. Opt. Lett. 2007, 32, 3056–3058. [Google Scholar] [CrossRef]
- Williams, P.A.; Swann, W.C.; Newbury, N.R. High-stability transfer of an optical frequency over long fiber-optic links. J. Opt. Soc. Am. B 2008, 25, 1284–1293. [Google Scholar] [CrossRef]
- Urick, V.J.; Bucholtz, F.; Devgan, P.S.; McKinney, J.D.; Williams, K.J. Phase modulation with interferometric detection as an alternative to intensity modulation with direct detection for analog-photonic links. IEEE Trans. Microw. Theory Tech. 2007, 55, 1978–1985. [Google Scholar] [CrossRef]
- Lopez, O.; Amy-Klein, A.; Daussy, C.; Chardonnet, C.; Narbonneau, F.; Lours, M.; Santarelli, G. 86-km optical link with a resolution of 2×10−18 for RF frequency transfer. Eur. Phys. J. D 2008, 48, 35–41. [Google Scholar] [CrossRef] [Green Version]
- Fujieda, M.; Kumagai, M.; Nagano, S. Coherent microwave transfer over a 204-km telecom fiber link by a cascaded system. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 168–174. [Google Scholar] [CrossRef]
- Liu, Q.; Han, S.L.; Wang, J.L.; Feng, Z.T.; Chen, W.; Cheng, N.; Gui, Y.Z.; Cai, H.W.; Han, S.S. Simultaneous frequency transfer and time synchronization over a 430 km fiber backbone network using a cascaded system. Chin. Opt. Lett. 2016, 14, 5. [Google Scholar] [CrossRef]
- Narbonneau, F.; Lours, M.; Bize, S.; Clairon, A.; Santarelli, G.; Lopez, O.; Daussy, C.; Amy-Klein, A.; Chardonnet, C. High resolution frequency standard dissemination via optical fiber metropolitan network. Rev. Sci. Instrum. 2006, 77, 064701. [Google Scholar] [CrossRef]
- Zhao, C.C.; Zhao, W.Y.; Xue, W.X.; Quan, H.L.; Yan, L.L.; Guo, W.G.; Jiang, H.F.; Zhang, S.G. Microwave frequency dissemination via 50 km optical Fiber based on optical delay compensation. Acta Photonica Sin. 2020, 49, 806002. [Google Scholar] [CrossRef]
- Gao, C.; Wang, B.; Zhu, X.; Yuan, Y.B.; Wang, L.J. Dissemination stability and phase noise characteristics in a cascaded, fiber-based long-haul radio frequency dissemination network. Rev. Sci. Instrum. 2015, 86, 093111. [Google Scholar] [CrossRef]
- Bousonville, M.; Rausch, J. Velocity of signal delay changes in fibre optic cables. In Proceedings of the 9th European Workshop on Beam Diagnostics and Instrumentation for Particle Accelerators, DIPAC 2009, Basel, Switzerland, 25–27 May 2009; pp. 248–250. [Google Scholar]
- Zhang, X.; Zhong, K.; Ming, H.; Jia, N.; Li, T.; Wang, A.X.; Wang, M.; Chi, J.; Sun, J. Experimental study on temperature dependence of dispersion of G.652 fiber and its effect on high speed optical communication system and compensation. In Proceedings of the Optoelectronic Devices and Integration III, Beijing, China, 22 November 2010. [Google Scholar]









| Works | L (km) | N | σy (1 s) | σy (104 s) | MF (GHz) |
|---|---|---|---|---|---|
| Ref. [33] | 430 | 2 | 19 × 10−14 | 13 × 10−17 | 1 |
| Ref. [32] | 204 | 2 | 6 × 10−14 | ~20 × 10−17 | 1 |
| Ref. [36] | 145 1 | 3 | 1.3 × 10−14 | 4.1 × 10−17 | 0.1 |
| This work | 300 1 | 3 | 1.1 × 10−14 | 5.3 × 10−17 | 9 |
| 9.0 × 10−15 | 3.8 × 10−17 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, W.; Zhao, W.; Quan, H.; Xing, Y.; Zhang, S. Cascaded Microwave Frequency Transfer over 300-km Fiber Link with Instability at the 10−18 Level. Remote Sens. 2021, 13, 2182. https://doi.org/10.3390/rs13112182
Xue W, Zhao W, Quan H, Xing Y, Zhang S. Cascaded Microwave Frequency Transfer over 300-km Fiber Link with Instability at the 10−18 Level. Remote Sensing. 2021; 13(11):2182. https://doi.org/10.3390/rs13112182
Chicago/Turabian StyleXue, Wenxiang, Wenyu Zhao, Honglei Quan, Yan Xing, and Shougang Zhang. 2021. "Cascaded Microwave Frequency Transfer over 300-km Fiber Link with Instability at the 10−18 Level" Remote Sensing 13, no. 11: 2182. https://doi.org/10.3390/rs13112182
APA StyleXue, W., Zhao, W., Quan, H., Xing, Y., & Zhang, S. (2021). Cascaded Microwave Frequency Transfer over 300-km Fiber Link with Instability at the 10−18 Level. Remote Sensing, 13(11), 2182. https://doi.org/10.3390/rs13112182