Improvement in Satellite Image-Based Land Cover Classification with Landscape Metrics
Abstract
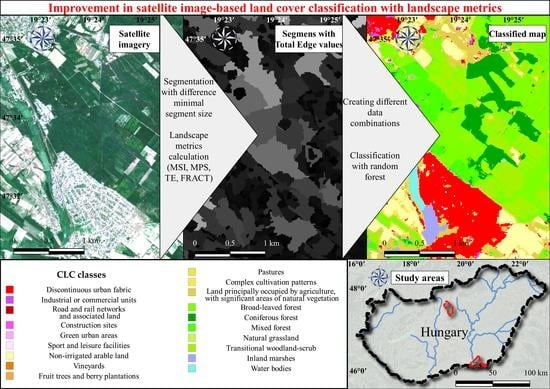
:1. Introduction
2. Study Areas
3. Materials and Methods
3.1. Remotely Sensed Data
3.2. Reference Land Cover Data (CORINE Land Cover 2018 Dataset)
3.3. Calculation of Landscape Metrics
3.4. Classification
4. Results
4.1. Influence of Segmentation on the Accuracy of Land Cover Mapping
4.2. Comparing the Accuracy of Land Cover Mapping Involving or Ignoring Landscape Indices
4.3. Scale Dependency of Classification Accuracy
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| User’s Accuracy | Spectral Bands | Spectral Bands and Segments | Spectral Bands and Landcsape Metrics | Spectral Bands, Segments and MSI | Spectral Bands, Segments and MPS | Spectral Bands, Segments and TE | Spectral Bands, Segments and FRACT | All Data |
|---|---|---|---|---|---|---|---|---|
| Discontinuous urban fabric | 87.7% | 89.5% | 89.7% | 90.3% | 90.2% | 90.0% | 90.2% | 91.5% |
| Road and rail networks and associated land | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% |
| Green urban areas | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% |
| Sport and leisure facilities | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| Non-irrigated arable land | 87.4% | 88.6% | 88.3% | 88.9% | 88.9% | 88.9% | 88.7% | 89.4% |
| Fruit trees and berry plantations | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 99.9% | 100.0% | 100.0% |
| Pastures | 86.3% | 88.0% | 88.1% | 88.6% | 88.4% | 88.3% | 88.5% | 89.5% |
| Complex cultivation patterns | 80.2% | 84.3% | 85.6% | 85.5% | 85.3% | 85.4% | 85.7% | 87.9% |
| Land principally occupied by agriculture, with significant areas of natural vegetation | 77.7% | 85.4% | 85.9% | 87.1% | 87.0% | 86.5% | 87.0% | 89.4% |
| Broad-leaved forest | 83.4% | 86.1% | 87.8% | 87.1% | 87.1% | 86.9% | 87.3% | 88.9% |
| Transitional woodland-scrub | 83.5% | 88.1% | 88.9% | 89.6% | 89.9% | 89.3% | 89.5% | 91.1% |
| Inland marshes | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% | 99.9% |
| Water courses | 97.4% | 97.7% | 97.7% | 97.7% | 97.8% | 97.8% | 97.7% | 97.9% |
| Water bodies | 100.0% | 99.9% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| Producer’s Accuracy | Spectral Bands | Spectral Bands and Segments | Spectral Bands and Landcsape Metrics | Spectral Bands, Segments and MSI | Spectral Bands, Segments and MPS | Spectral Bands, Segments and TE | Spectral Bands, Segments and FRACT | All Data |
|---|---|---|---|---|---|---|---|---|
| Discontinuous urban fabric | 81.2% | 81.6% | 81.9% | 81.7% | 81.7% | 81.7% | 81.7% | 82.0% |
| Road and rail networks and associated land | 37.9% | 49.7% | 50.1% | 52.3% | 52.3% | 49.8% | 53.2% | 56.1% |
| Green urban areas | 29.3% | 47.3% | 73.1% | 55.0% | 58.8% | 52.8% | 57.1% | 74.2% |
| Sport and leisure facilities | 35.8% | 48.9% | 56.7% | 53.6% | 52.7% | 53.1% | 53.7% | 62.4% |
| Non-irrigated arable land | 99.3% | 99.4% | 99.4% | 99.4% | 99.4% | 99.4% | 99.4% | 99.4% |
| Fruit trees and berry plantations | 43.1% | 51.3% | 74.9% | 59.7% | 64.2% | 65.2% | 58.4% | 72.7% |
| Pastures | 70.4% | 71.3% | 70.6% | 71.5% | 71.4% | 71.7% | 71.4% | 71.5% |
| Complex cultivation patterns | 26.0% | 32.2% | 31.2% | 34.3% | 34.2% | 33.7% | 33.3% | 37.3% |
| Land principally occupied by agriculture, with significant areas of natural vegetation | 38.9% | 41.1% | 42.8% | 42.6% | 42.2% | 42.0% | 42.8% | 45.6% |
| Broad-leaved forest | 88.7% | 89.2% | 89.0% | 89.3% | 89.1% | 89.3% | 89.3% | 89.3% |
| Transitional woodland-scrub | 69.0% | 74.8% | 80.9% | 76.5% | 79.3% | 78.3% | 77.6% | 84.8% |
| Inland marshes | 51.0% | 49.9% | 63.7% | 53.8% | 52.0% | 51.6% | 55.9% | 61.9% |
| Water courses | 83.9% | 84.4% | 84.4% | 84.8% | 84.6% | 84.3% | 84.8% | 85.0% |
| Water bodies | 39.1% | 45.3% | 42.4% | 44.9% | 46.0% | 46.1% | 44.8% | 45.9% |
| User’s Accuracy | Spectral Bands | Spectral Bands and Segments | Spectral Bands and Landcsape Metrics | Spectral Bands, Segments and MSI | Spectral Bands, Segments and MPS | Spectral Bands, Segments and TE | Spectral Bands, Segments and FRACT | All Data |
|---|---|---|---|---|---|---|---|---|
| Discontinuous urban fabric | 72.9% | 77.6% | 76.9% | 73.6% | 77.3% | 77.0% | 77.2% | 77.5% |
| Industrial or commercial units | 67.9% | 84.0% | 75.7% | 79.2% | 77.3% | 79.3% | 78.8% | 79.4% |
| Road and rail networks and associated land | 95.2% | 98.5% | 98.1% | 97.1% | 98.3% | 98.4% | 98.3% | 98.2% |
| Construction sites | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| Green urban areas | 99.0% | 99.8% | 99.6% | 99.6% | 99.8% | 99.7% | 99.7% | 99.8% |
| Sport and leisure facilities | 94.7% | 99.3% | 99.1% | 97.7% | 99.2% | 99.2% | 99.2% | 99.3% |
| Non-irrigated arable land | 70.6% | 75.1% | 73.3% | 73.2% | 73.7% | 73.9% | 74.1% | 74.0% |
| Vineyards | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| Fruit trees and berry plantations | 92.2% | 98.6% | 98.0% | 95.9% | 98.2% | 98.4% | 98.1% | 98.2% |
| Pastures | 62.0% | 81.3% | 74.1% | 73.7% | 75.9% | 76.8% | 76.3% | 76.2% |
| Complex cultivation patterns | 49.0% | 70.9% | 64.0% | 61.8% | 66.1% | 66.5% | 65.8% | 66.9% |
| Land principally occupied by agriculture, with significant areas of natural vegetation | 46.5% | 73.4% | 62.1% | 63.3% | 64.6% | 67.2% | 66.1% | 64.8% |
| Broad-leaved forest | 64.3% | 68.1% | 66.5% | 66.0% | 66.8% | 66.9% | 66.9% | 67.0% |
| Coniferous forest | 81.2% | 85.7% | 84.2% | 83.7% | 84.5% | 84.6% | 84.6% | 84.8% |
| Mixed forest | 58.7% | 73.8% | 68.9% | 66.0% | 70.0% | 70.6% | 70.8% | 70.2% |
| Natural grassland | 94.2% | 98.3% | 97.7% | 96.7% | 98.1% | 98.0% | 98.0% | 97.9% |
| Transitional woodland-scrub | 54.6% | 66.5% | 61.5% | 60.9% | 63.2% | 63.0% | 63.2% | 63.0% |
| Inland marshes | 96.3% | 99.0% | 98.2% | 98.0% | 98.6% | 98.4% | 98.5% | 98.5% |
| Water bodies | 95.1% | 98.4% | 96.5% | 97.7% | 96.7% | 97.7% | 97.5% | 97.6% |
| Producer’s Accuracy | Spectral Bands | Spectral Bands and Segments | Spectral Bands and Landcsape Metrics | Spectral Bands, Segments and MSI | Spectral Bands, Segments and MPS | Spectral Bands, Segments and TE | Spectral Bands, Segments and FRACT | All Data |
|---|---|---|---|---|---|---|---|---|
| Discontinuous urban fabric | 84.3% | 86.1% | 85.2% | 86.2% | 86.5% | 86.5% | 86.3% | 87.0% |
| Industrial or commercial units | 45.8% | 55.5% | 40.8% | 55.6% | 53.4% | 53.7% | 56.0% | 51.8% |
| Road and rail networks and associated land | 25.2% | 37.1% | 24.1% | 38.2% | 35.9% | 36.4% | 38.8% | 36.4% |
| Construction sites | 10.8% | 26.9% | 20.7% | 29.1% | 28.8% | 28.7% | 28.7% | 37.3% |
| Green urban areas | 9.7% | 19.6% | 15.4% | 21.3% | 20.7% | 21.1% | 23.2% | 27.1% |
| Sport and leisure facilities | 15.9% | 21.9% | 22.7% | 24.3% | 24.5% | 23.7% | 22.9% | 29.0% |
| Non-irrigated arable land | 96.6% | 96.4% | 96.6% | 96.4% | 96.4% | 96.5% | 96.4% | 96.5% |
| Vineyards | 30.7% | 36.8% | 55.8% | 41.0% | 41.0% | 42.3% | 43.3% | 54.5% |
| Fruit trees and berry plantations | 23.7% | 27.8% | 33.1% | 28.5% | 29.1% | 29.0% | 28.7% | 31.9% |
| Pastures | 41.2% | 42.0% | 46.9% | 43.1% | 43.4% | 44.0% | 43.9% | 47.2% |
| Complex cultivation patterns | 34.5% | 43.1% | 38.8% | 43.6% | 45.4% | 44.4% | 44.1% | 47.1% |
| Land principally occupied by agriculture, with significant areas of natural vegetation | 26.4% | 30.1% | 29.6% | 30.7% | 30.9% | 31.0% | 31.0% | 31.9% |
| Broad-leaved forest | 92.3% | 93.5% | 93.3% | 93.6% | 93.8% | 93.7% | 93.7% | 94.2% |
| Coniferous forest | 57.8% | 60.6% | 60.5% | 61.2% | 61.2% | 61.4% | 60.8% | 62.3% |
| Mixed forest | 44.8% | 53.1% | 48.4% | 53.4% | 53.2% | 53.8% | 54.3% | 56.4% |
| Natural grassland | 18.0% | 23.4% | 30.9% | 26.0% | 25.9% | 25.9% | 25.1% | 31.8% |
| Transitional woodland-scrub | 41.8% | 46.0% | 46.0% | 46.8% | 47.4% | 47.2% | 46.9% | 49.6% |
| Inland marshes | 15.8% | 20.9% | 25.0% | 22.5% | 23.7% | 23.9% | 23.6% | 30.9% |
| Water bodies | 43.6% | 48.2% | 43.9% | 49.2% | 49.1% | 48.8% | 50.2% | 47.8% |
References
- Jensen, J.R.; Rutchey, K.; Koch, M.S.; Narumalani, S. Inland wetland change detection in the Everglades Water Conservation Area 2A using a time series of normalized remotely sensed data. Photogramm. Eng. Remote Sens. 1995, 61, 199–209. [Google Scholar]
- Gabiri, G.; Diekkrüger, B.; Näschen, K.; Leemhuis, C.; Van Der Linden, R.; Majaliwa, J.-G.M.; Obando, J.A. Impact of Climate and Land Use/Land Cover Change on the Water Resources of a Tropical Inland Valley Catchment in Uganda, East Africa. Climate 2020, 8, 83. [Google Scholar] [CrossRef]
- Jensen, J.R.; Cowen, D.J. Remote sensing of urban/suburban infrastructure and socio-economic attributes. Photogramm. Eng. Remote Sens. 1999, 65, 611–622. [Google Scholar]
- Mishra, B.K.; Mebeelo, K.; Chakraborty, S.; Kumar, P.; Gautam, A. Implications of urban expansion on land use and land cover: Towards sustainable development of Mega Manila, Philippines. Geojournal 2019, 1–16. [Google Scholar] [CrossRef]
- Nobre, C.A.; Sampaio, G.; Borma, L.S.; Castilla-Rubio, J.C.; Silva, J.S.; Cardoso, M. Land-use and climate change risks in the Amazon and the need of a novel sustainable development paradigm. Proc. Natl. Acad. Sci. USA 2016, 113, 10759–10768. [Google Scholar] [CrossRef] [Green Version]
- Shumilo, L.; Kolotii, A.; Lavreniuk, M.; Yailymov, B. Use of Land Cover Maps as Indicators for Achieving Sustainable Development Goals. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 830–833. [Google Scholar] [CrossRef]
- Gibas, P.; Majorek, A. Analysis of Land-Use Change between 2012–2018 in Europe in Terms of Sustainable Development. Land 2020, 9, 46. [Google Scholar] [CrossRef] [Green Version]
- Edash, J.; Mathur, A.; Foody, G.M.; Curran, P.J.; Chipman, J.W.; Lillesand, T.M. Land cover classification using multi-temporal MERIS vegetation indices. Int. J. Remote Sens. 2007, 28, 1137–1159. [Google Scholar] [CrossRef] [Green Version]
- Zhou, T.; Li, Z.; Pan, J. Multi-Feature Classification of Multi-Sensor Satellite Imagery Based on Dual-Polarimetric Sentinel-1A, Landsat-8 OLI, and Hyperion Images for Urban Land-Cover Classification. Sensors 2018, 18, 373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fragoso-Campón, L.; Quirós, E.; Mora, J.; Gallego, J.A.G.; Durán-Barroso, P. Accuracy Enhancement for Land Cover Classification Using LiDAR and Multitemporal Sentinel 2 Images in a Forested Watershed. Proceedings 2018, 2, 1280. [Google Scholar] [CrossRef] [Green Version]
- Costachioiu, T.; Datcu, M. Land cover dynamics classification using multi-temporal spectral indices from satellite image time series. In Proceedings of the 2010 8th International Conference on Communications, Bucharest, Romania, 10–12 June 2010. [Google Scholar] [CrossRef]
- Thakkar, A.K.; Desai, V.R.; Patel, A.; Potdar, M.B. Land Use / Land Cover Classification of Remote Sensing Data and Their Derived Products in a Heterogeneous Landscape of a Khan-Kali Watershed, Gujarat. Asian J. Geoinform. 2014, 14, 1–12. [Google Scholar]
- Ayala-Izurieta, J.E.; Márquez, C.O.; García, V.J.; Recalde, C.; Llerena, M.V.R.; Damián-Carrión, D.A. Land Cover Classification in an Ecuadorian Mountain Geosystem Using a Random Forest Classifier, Spectral Vegetation Indices, and Ancillary Geographic Data. Geoscience 2017, 7, 34. [Google Scholar] [CrossRef] [Green Version]
- Narumalani, S.; Zhou, Y.; Jelinski, D.E. Utilizing geometric attributes of spatial information to improve digital image classification. Remote Sens. Rev. 1998, 16, 233–253. [Google Scholar] [CrossRef]
- Southworth, J.; Nagendra, H.; Tucker, C. Fragmentation of a Landscape: Incorporating landscape metrics into satellite analyses of land-cover change. Landsc. Res. 2002, 27, 253–269. [Google Scholar] [CrossRef]
- Frohn, R.C. The use of landscape pattern metrics in remote sensing image classification. Int. J. Remote Sens. 2006, 27, 2025–2032. [Google Scholar] [CrossRef]
- Hurni, K.; Hett, C.; Epprech, M.; Messerli, P.; Heinimann, A. A Texture-Based Land Cover Classification for the Delineation of a Shifting Cultivation Landscape in the Lao PDR Using Landscape Metrics. Remote Sens. 2013, 5, 3377–3396. [Google Scholar] [CrossRef] [Green Version]
- Han, N.; Du, H.; Zhou, G.; Xu, X.; Ge, H.; Liu, L.; Gao, G.; Sun, S. Exploring the synergistic use of multi-scale image object metrics for land-use/land-cover mapping using an object-based approach. Int. J. Remote Sens. 2015, 36, 3544–3562. [Google Scholar] [CrossRef]
- Yu, L.; Su, J.; Li, C.; Wang, L.; Ze, L.; Yan, B. Improvement of Moderate Resolution Land Use and Land Cover Classification by Introducing Adjacent Region Features. Remote Sens. 2018, 10, 414. [Google Scholar] [CrossRef] [Green Version]
- Grippa, T.; Georganos, S.; Zarougui, S.; Bognounou, P.; Diboulo, E.; Forget, Y.; Lennert, M.; VanHuysse, S.; Mboga, N.; Wolff, E. Mapping Urban Land Use at Street Block Level Using OpenStreetMap, Remote Sensing Data, and Spatial Metrics. ISPRS Int. J. Geo-Inf. 2018, 7, 246. [Google Scholar] [CrossRef] [Green Version]
- Uuemaa, E.; Antrop, M.; Roosaare, J.; Marja, R.; Mander, Ü. Landscape Metrics and Indices: An Overview of Their Use in Landscape Research. Living Rev. Landsc. Res. 2009, 3, 3. [Google Scholar] [CrossRef]
- Fichera, C.R.; Modica, G.; Pollino, M. Land Cover classification and change-detection analysis using multi-temporal remote sensed imagery and landscape metrics. Eur. J. Remote Sens. 2012, 45, 1–18. [Google Scholar] [CrossRef]
- Szilassi, P.; Bata, T.; Szabó, S.; Czúcz, B.; Molnár, Z.; Mezősi, G. The link between landscape pattern and vegetation naturalness on a regional scale. Ecol. Indic. 2017, 81, 252–259. [Google Scholar] [CrossRef] [Green Version]
- Lausch, A. Applicability of landscape metrics for the monitoring of landscape change: Issues of scale, resolution and interpretability. Ecol. Indic. 2002, 2, 3–15. [Google Scholar] [CrossRef]
- Peng, J.; Wang, Y.; Ye, M.; Wu, J.; Zhang, Y. Effects of land-use categorization on landscape metrics: A case study in urban landscape of Shenzhen, China. Int. J. Remote Sens. 2007, 28, 4877–4895. [Google Scholar] [CrossRef]
- Liu, D.; Hao, S.; Liu, X.; Li, B.; He, S.; Warrington, D.N. Effects of land use classification on landscape metrics based on remote sensing and GIS. Environ. Earth Sci. 2012, 68, 2229–2237. [Google Scholar] [CrossRef]
- Singh, S.K.; Laari, P.B.; Mustak, S.; Srivastava, P.K.; Szabó, S. Modelling of land use land cover change using earth observation data-sets of Tons River Basin, Madhya Pradesh, India. Geocarto Int. 2017, 33, 1202–1222. [Google Scholar] [CrossRef]
- Kumar, M.; Denis, D.M.; Singh, S.K.; Szabó, S.; Suryavanshi, S. Landscape metrics for assessment of land cover change and fragmentation of a heterogeneous watershed. Remote Sens. Appl. Soc. Environ. 2018, 10, 224–233. [Google Scholar] [CrossRef] [Green Version]
- Csikos, N.; Szilassi, P. Impact of Energy Landscapes on the Abundance of Eurasian Skylark (Alauda arvensis), an Example from North Germany. Sustainability 2020, 12, 664. [Google Scholar] [CrossRef] [Green Version]
- Szabó, S.; Csorba, P.; Szilassi, P. Tools for landscape ecological planning—Scale, and aggregation sensitivity of the contagion type landscape metric indices. Carpathian J. Earth Environ. Sci. 2012, 7, 127–136. [Google Scholar]
- Jiao, L.; Liu, Y.; Li, H. Characterizing land-use classes in remote sensing imagery by shape metrics. ISPRS J. Photogramm. Remote Sens. 2012, 72, 46–55. [Google Scholar] [CrossRef]
- Sertel, E.; Topaloğlu, R.H.; Şallı, B.; Algan, I.Y.; Aksu, G.A. Comparison of Landscape Metrics for Three Different Level Land Cover/Land Use Maps. ISPRS Int. J. Geo-Information 2018, 7, 408. [Google Scholar] [CrossRef] [Green Version]
- Büttner, G.; Kosztra, B. CLC2018 Technical Guidelines, 2017, European Environmental Agency and European Topic Centre on Urban, Land and Soil Systems (ETC/ULS); Environment Agency: Vienna, Austria, 2017. [Google Scholar]
- Szilassi, P. Land cover variability and the changes of land cover pattern in landscape units of Hungary. J. Landsc. Ecol. 2017, 15, 131–138. [Google Scholar]
- Mucsi, L.; Henits, L. Creating excess water inundation maps by sub-pixel classification of medium resolution satellite images. J. Environ. Geogr. 2010, 3, 31–40. [Google Scholar]
- Phiri, D.; Morgenroth, J. Developments in Landsat Land Cover Classification Methods: A Review. Remote Sens. 2017, 9, 967. [Google Scholar] [CrossRef] [Green Version]
- Henits, L.; Mucsi, L.; Liska, C.M. Monitoring the changes in impervious surface ratio and urban heat island intensity between 1987 and 2011 in Szeged, Hungary. Environ. Monit. Assess. 2017, 189, 189. [Google Scholar] [CrossRef]
- European Comission, Sentinel User Handbook and Exploration Tools (SUHET). Sentinel-2 User Handbook; ESA: Paris, France, 2015; Issue 1, Revision 2. [Google Scholar]
- Büttner, G.; Feranec, J.; Jaffrain, G.; Mari, L.; Maucha, G.; Soukup, T. The CORINE land cover 2000 project. EARSeL eProc. 2004, 3, 331–346. [Google Scholar]
- Comber, A.J.; Birnie, R.V.; Hodgson, M. Using landscape metrics to model land cover change. In Proceedings of the 9th Annual Conference of the International-Association-for-Landscape Ecology, Bangor, UK, 7–9 September 2000; pp. 143–161. [Google Scholar]
- Szabó, S. Tájmetriai Mérőszámok Alkalmazási Lehetőségeinek Vizsgálata a Tájanalízisben. Ph.D. Thesis, University of Debrecen, Debrecen, Hungary, 2009. [Google Scholar]
- Walz, U. Landscape Structure, Landscape Metrics and Biodiversity. Living Rev. Landsc. Res. 2011, 5, 5. [Google Scholar] [CrossRef]
- Sinha, P.; Kumar, L.; Reid, N. Rank-Based Methods for Selection of Landscape Metrics for Land Cover Pattern Change Detection. Remote Sens. 2016, 8, 107. [Google Scholar] [CrossRef] [Green Version]
- Cushman, S.A.; McGarigal, K.; Neel, M.C. Parsimony in landscape metrics: Strength, universality, and consistency. Ecol. Indic. 2008, 8, 691–703. [Google Scholar] [CrossRef]
- Turner, M.G. Landscape Ecology: The Effect of Pattern on Process, 1. Annu. Rev. Ecol. Syst 1989, 20, 171–197. [Google Scholar] [CrossRef]
- Blaschke, T. The role of the spatial dimension within the framework of sustainable landscapes and natural capital. Landsc. Urban Plan. 2006, 75, 198–226. [Google Scholar] [CrossRef]
- Eibe, F.; Mark, A.H.; Ian, H.W. The WEKA Workbench, Online Appendix. In Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Morgan Kaufmann: Cambridge, MA, USA, 2016. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Stuckens, J.; Coppin, P.; Bauer, M. Integrating Contextual Information with per-Pixel Classification for Improved Land Cover Classification. Remote Sens. Environ. 2000, 71, 282–296. [Google Scholar] [CrossRef]
- Aguirre-Gutiérrez, J.; Seijmonsbergen, A.C.; Duivenvoorden, J.F. Optimizing land cover classification accuracy for change detection, a combined pixel-based and object-based approach in a mountainous area in Mexico. Appl. Geogr. 2012, 34, 29–37. [Google Scholar] [CrossRef] [Green Version]
- Senthilnath, J.; Bajpai, S.; Omkar, S.; Diwakar, P.; Mani, V. An approach to multi-temporal MODIS image analysis using image classification and segmentation. Adv. Space Res. 2012, 50, 1274–1287. [Google Scholar] [CrossRef]
- Zanotta, D.C.; Zortea, M.; Ferreira, M.P. A supervised approach for simultaneous segmentation and classification of remote sensing images. ISPRS J. Photogramm. Remote Sens. 2018, 142, 162–173. [Google Scholar] [CrossRef]
- Chust, G.; Ducrot, D.; Pretus, J.L. Land cover mapping with patch-derived landscape indices. Landsc. Urban Plan. 2004, 69, 437–449. [Google Scholar] [CrossRef]






| Code | Gödöllői-Hills | Marosszög |
|---|---|---|
| 1.1.2. Discontinuous urban fabric | 10.39% | 6.20% |
| 1.2.1. Industrial or commercial units | 1.33% | 0.28% |
| 1.2.2. Road and rail networks and associated land | 0.38% | 0.02% |
| 1.3.3. Construction sites | 0.09% | 0.00% |
| 1.4.1. Green urban areas | 0.14% | 0.07% |
| 1.4.2. Sport and leisure facilities | 0.35% | 0.13% |
| 2.1.1. Non-irrigated arable land | 35.75% | 74.55% |
| 2.2.1. Vineyards | 0.11% | 0.00% |
| 2.2.2. Fruit trees and berry plantations | 0.75% | 0.06% |
| 2.3.1. Pastures | 2.43% | 5.99% |
| 2.4.2. Complex cultivation patterns | 3.28% | 2.15% |
| 2.4.3. Land principally occupied by agriculture, with significant areas of natural vegetation | 2.52% | 1.79% |
| 3.1.1. Broad-leaved forest | 29.64% | 6.50% |
| 3.1.2. Coniferous forest | 2.30% | 0.00% |
| 3.1.3. Mixed forest | 2.78% | 0.00% |
| 3.2.1. Natural grassland | 0.45% | 0.00% |
| 3.2.4. Transitional woodland scrub | 6.77% | 0.75% |
| 4.1.1. Inland marshes | 0.21% | 0.07% |
| 5.1.1. Water courses | 0.00% | 1.30% |
| 5.1.2. Water bodies | 0.32% | 0.14% |
| Feature | Index | Name and Description |
|---|---|---|
| Area | MPS | Mean Patch Size |
| where aij represents the area of the jth patch in the ith class, ni represents the number of patches in the ith class and n represents the number of patches (>0) | ||
| Edges | TE | Total Edge |
| , | ||
| where eik represents the edge length between the ith and kth patch types and m represents the number of patch classes (≤0) | ||
| Shape Complexity | MSI | Mean Shape Index |
| , | ||
| where pij represents the perimeter of the jth patch in class ith, aij represents the area of the jth patch in class ith, ni represents the number of patches in the ith class and n represents the number of patches (≥1) | ||
| MFRACT | Mean Fractal Dimension | |
| where pij represents the perimeter of the jth patch in class ith, aij represents the area of the jth patch in class ith, ni represents the number of patches in the ith class and n represents the number of patches (1–2) |
| Study Area | Data | 1 ha | +% | 5 ha | +% | 10 ha | +% | 25 ha | +% |
|---|---|---|---|---|---|---|---|---|---|
| Marosszög | Spectral bands | 87.02% | - | 86.92% | - | 87.02% | - | 87.02% | - |
| Spectral bands + segments | 88.50% | 1.48% | 88.46% | 1.53% | 90.16% | 3.14% | 88.17% | 1.15% | |
| Gödöllői-hills | Spectral bands | 66.81% | - | 66.86% | - | 66.81% | - | 66.81% | - |
| Spectral bands + segments | 70.91% | 4.10% | 71.07% | 4.21% | 70.79% | 3.98% | 70.92% | 4.11% |
| Marosszög 1 ha | Marosszög 5 ha | Marosszög 10 ha | Marosszög 25 ha | Gödöllői-Hills 1 ha | Gödöllői-Hills 5 ha | Gödöllői-Hills 10 ha | Gödöllői-Hills 25 ha | |
|---|---|---|---|---|---|---|---|---|
| Number of segments | 11,730 | 5283 | 271 | 209 | 9971 | 9971 | 2182 | 831 |
| Mean segment size (ha) | 12.6 | 28.0 | 545.4 | 707.3 | 9.3 | 9.3 | 42.6 | 111.8 |
| Modus (ha) | 1.3 | 8.9 | 13.9 | - | 1.0 | - | 12.5 | 27.1 |
| Marosszög | Gödöllői-Hills | |||||||
|---|---|---|---|---|---|---|---|---|
| Data/Minimal segment size | 1 ha | 5 ha | 10 ha | 25 ha | 1 ha | 5 ha | 10 ha | 25 ha |
| Spectral bands | 87.02% | 87.02% | 87.02% | 87.02% | 66.81% | 66.81% | 66.81% | 66.81% |
| Spectral bands and segments | +1.48% | +1.53% | +3.14% | +1.15% | +4.10% | +4.21% | +3.98% | +4.11% |
| Spectral bands and landscape metrics | +0.59% | +1.51% | +2.65% | +2.38% | +2.82% | +3.55% | +4.96% | +6.82% |
| Spectral bands, segments and MSI | +3.28% | +2.01% | +1.89% | +1.92% | +4.65% | +4.87% | +5.16% | +5.82% |
| Spectral bands, segments and MPS | +3.35% | +2.00% | +3.70% | +1.71% | +4.97% | +5.06% | +5.10% | +5.65% |
| Spectral bands, segments and TE | +3.39% | +1.91% | +3.80% | +1.88% | +4.87% | +5.10% | +5.12% | +5.65% |
| Spectral bands, segments and MFRACT | +1.64% | +1.87% | +1.94% | +1.84% | +4.61% | +5.11% | +5.04% | +5.85% |
| All data (spectral bands, segments and landscape metrics) | +1.82% | +2.73% | +4.37% | +2.96% | +6.28% | +6.76% | +7.88% | +9.33% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gudmann, A.; Csikós, N.; Szilassi, P.; Mucsi, L. Improvement in Satellite Image-Based Land Cover Classification with Landscape Metrics. Remote Sens. 2020, 12, 3580. https://doi.org/10.3390/rs12213580
Gudmann A, Csikós N, Szilassi P, Mucsi L. Improvement in Satellite Image-Based Land Cover Classification with Landscape Metrics. Remote Sensing. 2020; 12(21):3580. https://doi.org/10.3390/rs12213580
Chicago/Turabian StyleGudmann, András, Nándor Csikós, Péter Szilassi, and László Mucsi. 2020. "Improvement in Satellite Image-Based Land Cover Classification with Landscape Metrics" Remote Sensing 12, no. 21: 3580. https://doi.org/10.3390/rs12213580
APA StyleGudmann, A., Csikós, N., Szilassi, P., & Mucsi, L. (2020). Improvement in Satellite Image-Based Land Cover Classification with Landscape Metrics. Remote Sensing, 12(21), 3580. https://doi.org/10.3390/rs12213580