Next Article in Journal
Recent Ground Subsidence in the North China Plain, China, Revealed by Sentinel-1A Datasets
Next Article in Special Issue
Using GRACE Data to Study the Impact of Snow and Rainfall on Terrestrial Water Storage in Northeast China
Previous Article in Journal
Improvement in Satellite Image-Based Land Cover Classification with Landscape Metrics
Previous Article in Special Issue
Preliminary Estimation and Validation of Polar Motion Excitation from Different Types of the GRACE and GRACE Follow-On Missions Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 21
10.3390/rs12213578
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Spatio-Temporal Evaluation of Water Storage Trends from Hydrological Models over Australia Using GRACE Mascon Solutions

by
Xinchun Yang
1,2,
Siyuan Tian
3,
Wei Feng
4,
Jiangjun Ran
5,
Wei You
1,*,
Zhongshan Jiang
1 and
Xiaoying Gong
1
1
Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China
2
School of Environment and Resource, Southwest University of Science and Technology, Mianyang 621010, China
3
Fenner School of Environment & Society, Australian National University, Canberra 2601, Australia
4
State Key Laboratory of Geodesy and Earth’s Dynamics, Institute of Geodesy and Geophysics, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430077, China
5
Department of Earth and Space Sciences, Southern University of Science and Technology, Shenzhen 518055, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(21), 3578; https://doi.org/10.3390/rs12213578
Submission received: 20 September 2020 / Revised: 28 October 2020 / Accepted: 30 October 2020 / Published: 31 October 2020
(This article belongs to the Special Issue GRACE Satellite Gravimetry for Geosciences)
Browse Figures
Versions Notes

Abstract

:
The Gravity Recovery and Climate Experiment (GRACE) data have been extensively used to evaluate the total terrestrial water storage anomalies (TWSA) from hydrological models. However, which individual water storage components (i.e., soil moisture storage anomalies (SMSA) or groundwater water storage anomalies (GWSA)) cause the discrepancies in TWSA between GRACE and hydrological models have not been thoroughly investigated or quantified. In this study, we applied GRACE mass concentration block (mascon) solutions to evaluate the spatio-temporal TWSA trends (2003–2014) from seven prevailing hydrological models (i.e., Noah-3.6, Catchment Land Surface Model (CLSM-F2.5), Variable Infiltration Capacity macroscale model (VIC-4.1.2), Water—Global Assessment and Prognosis (WaterGAP-2.2d), PCRaster Global Water Balance (PCR-GLOBWB-2), Community Land Model (CLM-4.5), and Australian Water Resources Assessment Landscape model (AWRA-L v6)) in Australia and, more importantly, identified which individual water storage components lead to the differences in TWSA trends between GRACE and hydrological models. The results showed that all of the hydrological models employed in this study, except for CLM-4.5 model, underestimated the GRACE-derived TWSA trends. These underestimations can be divided into three categories: (1) ignoring GWSA, e.g., Noah-3.6 and VIC-4.1.2 models; (2) underrating both SMSA and GWSA, e.g., CLSM-F2.5, WaterGAP-2.2d, and PCR-GLOBWB-2 models; (3) deficiently modeling GWSA, e.g., AWRA-L v6 model. In comparison, CLM-4.5 model yielded the best agreement with GRACE but overstated the GRACE-derived TWSA trends due to the overestimation of GWSA. Our results underscore that GRACE mascon solutions can be used as a valuable and efficient validation dataset to evaluate the spatio-temporal performance of hydrological models. Confirming which individual water storage components result in the discrepancies in TWSA between GRACE and hydrological models can better assist in further hydrological model development.

Graphical Abstract

1. Introduction

Accurate quantification of total terrestrial water storage anomalies (TWSA) is indispensable for the prediction of regional food supply, energy production, human and ecosystem health, and economic and societal development [1], particularly in arid and semi-arid environments (e.g., Australia). Since the first primitive land surface model introduced by Manabe in 1969 [2], many tens of hydrological models have been employed to analyze TWSA. Due to different model structures and parameterizations utilized in hydrological models, significant discrepancies can be observed among these model-simulated water storage variations in Australia. For instance, although Water—Global Assessment and Prognosis (WaterGAP-2.2) model [3] and Community Land Model version 4.0 (CLM-4.0) [4] include all water storage components, they have different climate forcing and soil thicknesses (more details about these models can be found in Section 2.2.1). Such differences cause a linear trend of TWSA (2002–2014) simulated by these two models in the Murray–Darling river basin to show opposite variation, i.e., 3.78 mm/year for WaterGAP model but −4.58 mm/year for CLM-4.0 model [5]. Hence, a question emerges about the reliability of hydrological models in Australia.
Encouragingly, satellite measurements of the Earth’s time-variable gravity from the Gravity Recovery and Climate Experiment (GRACE) mission provide new data for monitoring TWSA at the regional and global scales with a surface spatial resolution of 300 km [6]. In Australia, GRACE data have been used to monitor the Millennium Drought [7,8,9,10,11], groundwater variations [12,13], and the impacts of extreme hydroclimatic events (e.g., El Niño-Southern Oscillation (ENSO), Indian Ocean Dipole (IOD), and Southern Annular Mode (SAM)) on water change [9,14,15,16,17]. Additionally, due to the uncertainty of monthly GRACE-derived TWSA being at an error level of 2 cm in terms of equivalent water thickness (EWT) for a catchment of the size ≈63,000 km2 [18], and considering that this uncertainty could be decreased with the increase in catchment size (due to GRACE measurement and leakage uncertainties decreasing with increasing basin size [5]), GRACE data can also be used to evaluate the performance of hydrological models in Australia [19]. van Dijk et al. [20] used the TWSA derived from GRACE spherical harmonic (SH) solutions to test the performance of the TWSA modeled by the Australian Water Resources Assessment (AWRA) system in Australia and indicated that AWRA model tended to have smaller seasonal amplitude and to show less negative trends in northwest Australia, the southern Murray Basin, and southwest Western Australia than GRACE. Swenson et al. [21] used the TWSA derived from GRACE SH solutions to examine the response of the Community Land Model (CLM-4.5) aquifer model to transitions between low and high recharge inputs in a northeastern Australia region and showed that CLM-4.5 model simulates unrealistic long-period behavior relative to the TWSA derived from GRACE. Tangdamrongsub et al. [22] used the TWSA and groundwater water storage anomalies (GWSA) derived from GRACE data assimilation (GRACE DA; assimilates GRACE SH solutions into the PCRaster Global Water Balance (PCR-GLOBWB) model) to evaluate the performance of four different hydrological models (i.e., WaterGAP, PCR-GLOBWB, Community Atmosphere Biosphere Land Exchange (CABLE), and World-Wide Water (W3)) in Australia and the North China Plain. The results indicated that GRACE DA shows a significant improvement in all measures than those obtained from the model simulations alone. Scanlon et al. [5,23] used the TWSA derived from GRACE mass concentration block (mascon) and SH solutions to evaluate the reliability of two hydrological and water resource models (i.e., WaterGAP and PCR-GLOBWB) and five land surface models (i.e., Noah-3.3, Catchment Land Surface Model (CLSM-F2.5), Variable Infiltration Capacity macroscale model (VIC), Mosaic, and CLM-4.0) in 183 river basins globally (four river basins for Australia). The results showed that compared to GRACE, all models underestimated the large water storage trends and most models underestimated the seasonal water storage amplitudes in tropical and (semi) arid basins, while land surface models generally overestimated the amplitudes in northern basins. These studies focused on using GRACE data to evaluate the reliability of hydrological model-simulated TWSA in Australia, but less attention has been paid to which individual water storage components (i.e., soil moisture storage anomalies (SMSA) or GWSA) lead to the discrepancies in TWSA between GRACE and hydrological models. However, identifying and quantifying the contribution of individual water storage components to the discrepancies in TWSA between GRACE and hydrological models are critical for assessing continental water storage change and further hydrological model development [24]. Therefore, the manner in which individual water storage components affect the performance of hydrological models in Australia needs to be analyzed.
We assume that the total terrestrial water storage (TWS) in Australia is mainly composed of soil moisture storage (SMS) and groundwater storage (GWS), while the contribution of snow water storage (SnWS), canopy water storage (CWS), and surface water storage (SWS) are negligible (more details can be found in Section 2.3.1). The reference value of TWSA is based on the mean of three different GRACE mascon solutions (i.e., Center for Space Research release 6 (RL 06) mascon solutions v01 (CSR-M), Jet Propulsion Laboratory RL06 mascon solutions v01(JPL-M), and Goddard Space Flight Center mascon solutions v02.4 (GSFC-M)), the reference value of SMSA is the mean of four different hydrological models (i.e., Noah-3.6, VIC-4.1.2, CLM-4.5, and Australian Water Resources Assessment Landscape model (AWRA-L v6) models), and the reference value of GWSA is the residual between the reference value of TWSA and the reference value of SMSA. These three different reference values are used to evaluate the performance of hydrological models. This study aimed to use GRACE mascon solutions to evaluate the spatio-temporal performance of TWSA from hydrological models and identify which individual water storage components (i.e., SMSA or GWSA) result in the discrepancies in TWSA between GRACE and hydrological models. The results can provide guidance for choosing the appropriate dataset when investigating different water storage variations and assist in the development of hydrological models in Australia.
The rest of the paper is organized as the follows. Section 2 presents the overview of the study area, hydrological models, and GRACE mason solutions, as well as describes the determination of the reference values (i.e., of the TWSA, SMSA, and GWSA) and the evaluation strategy. Section 3 presents a comparison of different GRACE mascon solutions, an evaluation of hydrological models, and a quality assessment of the contribution of SMSA trends and GWSA trends to the differences in TWSA trends between GRACE mascon solutions and hydrological models, as well as discusses the influence of the driving force from the model structure, climate forcing, human water use, and model calibration on the results. Section 4 concludes the key findings of this study.

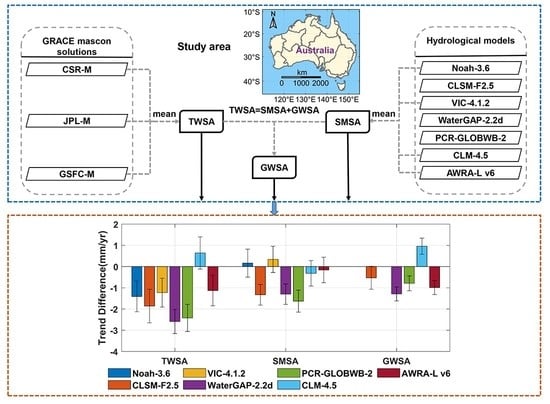
2. Data and Methods

2.1. Study Area

Australia is the only country in the world that covers an entire continent. This continent can be divided into 13 regions based on topographic drainage divisions [25] (Figure 1). Australia was selected as a study area due to the following reasons: first, only a reduction in leakage errors was required (the signal in a target region may leak into the surrounding areas and reduce signal amplitude in this region (leakage-out), and the signal from the surrounding areas may also leak into this region (leakage-in) and improve the signal amplitude in this region) across coastlines when GRACE data were used to analyze the TWSA over Australia [26], without considering contamination from other continents [27]. GRACE mascon solutions can easily satisfy this requirement [28] and are better for estimating small hydrological signals over Australia. Second, Australia has experienced significant spatio-temporal TWS variabilities under extreme hydroclimatic impacts [16], so measuring the water storage variations over Australia has long been proven to be a challenge for hydrological models [26]. Lastly, SMSA and GWSA are the major components of the TWSA in Australia, while snow water storage anomalies (SnWSA), canopy water storage anomalies (CWSA), and surface water storage anomalies (SWSA) are assumed to be negligible [22] (more details about these components are given in Section 2.3.1). Therefore, this feature can help us to better understand the primary water storage component that leads to the discrepancies in TWSA between GRACE data and a hydrological model. In this study, we focused on analyzing the water storage variations across the whole continent of Australia. Additionally, to help interpretation, we also quantized the water storage variations in four different regions (i.e., the Carpentaria Coast (CC), the North East Coast (NEC), the Murray–Darling Basin (MDB), and the North Western Plateau (NWP)) (Figure 1), which are typical regions of water storage changes in Australia (more details can be found in Section 3.1).

2.2. Data

2.2.1. Hydrological Models

A hydrological model, defined as a simplification of a real-world system, helps us to understand, predict, and manage water resources [29]. Hence, understanding the performance of hydrological models is important. In this study, we assessed the performance of seven state-of-the-art hydrological models that are commonly used in Australia [12,13,20,22]. These hydrological models include three different land surface models (i.e., Noah-3.6, CLSM-F2.5, and VIC-4.1.2) in Global Land Data Assimilation System (GLDAS-2.1) [30], as well as Water—Global Assessment and Prognosis (WaterGAP-2.2d) [3], PCRaster Global Water Balance (PCR-GLOBWB-2) [31], CLM-4.5 [32], and Australian Water Resources Assessment Landscape model (AWRA-L v6) models [33]. Their primary attributes are listed in Table 1. The key differences between hydrological models are model structure, climate forcing input, consideration of human water use or not, and model calibration. For instance, most of the hydrological models used in this study include all individual water storage components, whereas Noah-3.6 and VIC-4.1.2 models do not contain SWS, or GWS. Additionally, the soil thicknesses among hydrological models are different, e.g., the soil depth of VIC-4.1.2 in Australia is from 1.5 to 3.5 m [34], and from 0.5 to 1.5 m for WaterGAP-2.2d model in most parts of Australia [3]. For climate forcing, only Noah-3.6, CLSM-F2.5, and VIC-4.1.2 models use the same parameters, whereas the other hydrological models utilize completely different parameters. Furthermore, only WaterGAP-2.2d model considers human water use and model calibration. In summary, these differences can affect the performance of these models, and are the focus of this study.

2.2.2. GRACE Mascon Solutions

The GRACE twin satellites [6], their science mission launched on 17 March 2002 and ended on 12 October 2017, were a joint space mission of National Aeronautics and Space Administration (NASA) and German Aerospace Center (DLR). Its primary objective was to monitor the temporal changes of the Earth’s gravity field at the global scale [19]. The temporal variations of the Earth’s gravity field are mainly caused by earthquakes [35], crustal deformations [36], glacial isostatic adjustment [37], and oceanic [38] and hydrologic processes [19]. Across Australia, GRACE-derived gravity changes were generally attributed to large-scale hydrological variations [39,40].
Three newly available GRACE mascon solutions were employed in this study to analyze the TWS changes in Australia, i.e., Center for Space Research release 06 (RL 06) mascon solutions v01 (CSR-M) [41,42], Jet Propulsion Laboratory RL06 mascon solutions v01 (JPL-M) [43,44], and Goddard Space Flight Center mascon solutions v02.4 (GSFC-M) [45]. Their primary processing details are listed in Table 2. Compared to GRACE SH solutions, there are two main advantages of mascon solutions when using them to study the water storage changes in Australia. First, mascon solutions can be applied from the regional to global scales, whereas SH solutions are just for the global scale [28]. Hence, mascon solutions can better resolve ocean leakage error in terrestrial water signals across Australia [26,46]. Second, mascon solutions apply geophysical data constraints during processing with little empirical post-processing requirements, i.e., they do not require de-striping and signal restoration, which were necessary for the SH solutions [28]. Therefore, mascon solutions provide a higher signal-to-noise ratio [1], which is more suitable for the arid Australian environment with relatively small seasonal hydrological variations [26]. Although the spatial resolution of GRACE is only ~100,000 km2 (~3° × 3° at the equator) [28], it is suitable for measuring the TWS in a large-scale region [5] (e.g., for the whole continent of Australia).
It should be noted that the timelines of all datasets were chosen during the intersection of GRACE and hydrological models, that is, from January 2003 to December 2014 (Table 1 and Table 2). The missing months of data in GRACE mascon solutions were filled by linear interpolation. Since the monthly water anomalies from GRACE mascon solutions were typically computed relative to a time–mean baseline (Table 2), all water storages anomalies were computed relative to the same time–mean baseline (i.e., 2004.0–2009.999). Additionally, to ensure the consistency of the spatial resolution between GRACE and hydrological models, the spatial resolution of all data was interpolated to 0.5°. We found that the standard deviations between the interpolated data-derived TWSA and that of the corresponding original resolution data in Australia were lower than those between the different original resolution data. Therefore, although interpolation may affect the value of an individual grid cell, it can be ignored for the study of TWSA at the regional scale.

2.3. Methodology

2.3.1. Composition of Total Terrestrial Water Storage

Snow water storage (SnWS), canopy water storage (CWS), surface water storage (SWS), soil moisture storage (SMS), and groundwater storage (GWS) are the five individual components of total terrestrial water storage (TWS) [1,5], i.e.,
T W S = S n W S + C W S + S W S + S M S + G W S
Total terrestrial water storage anomaly (TWSA) is relative to a long-term mean TWS (e.g., the average of 2004.0–2009.999 in this study), generally expressed as an equivalent water thickness (EWT; unit: mm) [48]. The same interpretations are for SnWSA, CWSA, SWSA, SMSA, and GWSA. Under the Australian environment, SWS changes are expected to be minor and negligible [12]. Rodell et al. [49] indicated that the seasonal amplitude of the gravity changes caused by biomass variations is as large as 5 mm, but it was still at an order of magnitude smaller than the current GRACE uncertainties (2 cm); hence CWS changes are negligible. Additionally, SWS variations have little impact over most of Australia [50], and such variations are not considered as a major contributor to TWSA [40,50,51]. In summary, based on these assumptions, the water storage equation over Australia can be simplified as follows:
T W S A = S M S A + G W S A

2.3.2. Time Series Decomposition and Trend Estimation

The Seasonal Trend Decomposition using Loess procedure (STL), introduced by Cleveland et al. [52], is a versatile and robust decomposition method [53]. This method consists of inner and outer loops. In the inner loop, the seasonal and long-term components are estimated from a given time series under several passes of smoothing filters. In the outer loop, robustness weights, which are utilized in the next iteration of the inner loop, are adjusted to reduce the impact of outliers in the time series (more details can be found in the work of [53]). Compared to the outputs from harmonic analysis, which is a common approach used to remove seasonal variations from given time series data, the STL method shows similar results but isolates long-term components without additional smoothing [5]. Therefore, in the current study, the STL method was utilized to decompose the monthly time series of water storage anomalies into seasonal ( X s e a s o n a l ), long-term ( X l o n g − t e r m ), and residual ( X r e s i d u a l ) components as follows:
X t o t a l = X s e a s o n a l + X l o n g − t e r m + X r e s i d u a l
The long-term component was further decomposed into the X l i n e a r and X i n t e r − a n n u a l components by fitting a trend applying least squares linear regression and assigning the remaining long-term signal to inter-annual variability. The residual component included the unmodeled seasonal and long-term components and can reflect the sub-seasonal signal and noise [5].
The seasonal variability and linear trend (hereinafter called trend) in TWSA are important for understanding the related hydrological processes over specified regions [54]. They are usually selected as evaluation metrics to assess the performance of hydrological models [5,23]. However, for the TWSA over Australia, only some parts of the northern continent are dominated by seasonal variability [53]. Therefore, in this study, we focused on evaluating the performance of hydrological models based on the trends in water storage changes. Additionally, in order to assess the significance of the trends, the Mann–Kendall test (M–K test) [55,56] with a significance level of 0.05 was performed on long-term components data based on STL decomposition (Equation (3)). The M–K test, which is a non-parametric test for identifying whether or not there is a linear monotonic trend in a time series [57], has been widely utilized to detect trends in hydrologic data [58]. Additionally, the uncertainties in trends are mathematically derived from least squares linear regression when decomposing long-term components [28].

2.3.3. Determination of Reference Values

In this study, we not only assessed the TWSA trends derived from hydrological models, but also evaluated the trends of the individual water storage components of said hydrological models. To understand how different water storage components (i.e., soil moisture and groundwater) contribute to the differences in TWSA trends between GRACE and hydrological models, it is essential to determine the corresponding reference values of the different components.
Since GRACE-derived TWSA is an integrated change and cannot be decomposed into individual components without ancillary data, it has been widely used to evaluate modeled TWSA simulations. Additionally, we used the mean of three GRACE mascon solutions-based TWSA as a reference value for TWSA, which is more effective in reducing the noise in the gravity field solutions than an independent mascon solution [59]. The TWSA uncertainty was calculated based on the standard deviation among these GRACE mascon solutions [59].
Soil moisture storage changes are generally from one of the following three broad sources, namely, in situ observations, satellite remotely sensed estimates, and models simulations [60]. However, in situ measurements are at point-scale and are sparsely distributed across the continent of Australia [61]. Although remotely sensed soil moisture estimates can satisfy the spatial requirements, they usually represent the soil moisture in the top ~5 cm [62], which is much lower than the soil depth of hydrological models (Table 1). Therefore, in this study, we utilized the modeled SMSA as a reference value, which has been widely implemented in Australia [7,12,40,63]. Additionally, there is no definite way to identify which model demonstrates the highest accuracy; therefore, in order to reduce the influence of model uncertainty on the reliability of the reference valued, we adopted a multi-model (i.e., Noah-3.6, VIC-4.1.2, CLM-4.5, and AWRA-L v6 models; more details can be found in Section 3.2.2) ensemble average as a reference value of SMSA. The SMSA uncertainty was equal to the standard deviation among the applied models [51].
The variations in groundwater storage can be measured by in situ borehole observations; however, the spatial coverage of monitoring boreholes in Australia is inadequate and uneven [12,22]. These boreholes are mainly biased toward locations in the southern and southwestern parts and the eastern coast [64], which cannot satisfy the spatial requirement of this study on a continental scale. Moreover, the groundwater level from the monitoring of boreholes needs to be multiplied by a specific yield to convert it into groundwater storage, but the uncertainty in the special yield is very difficult to quantify [40]. Although most of the hydrological models used in this study include groundwater storage, large differences in GWSA trends between them were found (more details can be found in Section 3.2.3). Thus, selecting one model or a multi-model ensemble mean as a reference value was not reasonable. In comparison, GRACE-inferred groundwater storage, which was separated as the residual between the GRACE-based TWSA and the modeled SMSA [51,65,66], can provide a reasonable agreement with borehole-derived water storage for the regions with sufficient boreholes over Australia [7,12,22,40,67]. This suggests that GRACE-inferred GWSA can reliably be used as a reference value of GWSA, and the GWSA uncertainty was calculated by the root-sum-of-squares of two uncertainties from the TWSA and SMSA reference values [40].

2.3.4. Evaluation Strategy

In this study, we concentrated on using the differences (Equation (4)) in different water storage trends between hydrological models and the reference values as evaluation metrics to assess the performance of said hydrological models.
Δ t r e n d = t r e n d M − t r e n d O
where Δ t r e n d is the trend difference, t r e n d M is the water storage trend simulated by a hydrological model, and t r e n d O is the water storage trend derived from the reference value. If the value of Δ t r e n d is negative, it implies that the hydrological model underestimates the reference value of trend. It should be noted that the released spatial resolution of GRACE mascon solutions has the same or a higher resolution than that of hydrological models (Table 1 and Table 2) (e.g., the released spatial resolution of GSFC-M is 1° × 1°, the same as that of GLDAS-2.1 model). However, these grid cells in GRACE mascon solutions are highly correlated with their neighbors due to the native spatial resolution of GRACE being approximately 3° × 3° [1]. Therefore, any analysis of the result of an individual grid cell should be avoided [20,22]. In other words, the spatial pattern of different water storage trends was only used for visualization purposes, and the quantified metrics for evaluating the performance of hydrological models were based on the differences between the temporal trends.
Additionally, to aid interpretation, we estimated the temporal agreements in different water storage anomalies between hydrological models and the reference values using the following statistics: Pearson’s linear correlation coefficient (r: at the significance level p < 0.05), root-mean-square error (RMSE), and the Nash–Sutcliffe efficiency (NSE) coefficient, respectively, as follows:
r = ∑ i = 1 n ( M i − M ¯ ) ( O i − O ¯ ) ∑ i = 1 n ( M i − M ¯ ) 2 ∑ i = 1 n ( O i − O ¯ ) 2
R M S E = 1 n ∑ i = 1 n ( M i − O i ) 2
N S E = 1 − ∑ i = 1 n ( M i − O i ) 2 ∑ i = 1 n ( O i − O ¯ ) 2
where M i and O i are the modeled and reference values of the same variable, respectively; M ¯ and O ¯ are the mean of the modeled and reference values, respectively, i is the number of months, and n is the total number of months (i.e., 144 months).

3. Results and Discussion

3.1. Comparison of Total Terrestrial Water Storage Trends Derived from GRACE Mascon Solutions

The spatial distributions of the TWSA trends derived from three different GRACE mascon solutions are shown in Figure 2, while the temporal variations in the TWSA derived from three different GRACE mascon solutions based at the regional and continental scales are shown in Figure 3. As displayed in Figure 2a, the TWSA trends of CSR-M exhibited a bipolar pattern, with pronounced positive trends seen in CC (7.71 ± 0.84 mm/year; Figure 3a), NEC (10.98 ± 0.75 mm/year; Figure 3b), and MDB (7.41 ± 0.85 mm/year; Figure 3c), whereas significant negative trends can be observed in NWP (−6.84 ± 0.69 mm/year; Figure 3d). This pattern was also reported by Humphrey et al. [53] and Rodell et al. [1]. Meanwhile, the TWSA trends from JPL-M and GSFC-M experienced a similar distribution to that of CSR-M (Figure 2b,c and Figure 3a–d, and Table S1), but CSR-M displayed higher apparent resolution and gradual changes. This can be attributed to the fact that the regularization of the CSR mascon solutions is dependent on a 200-km Gaussian filter and its grid files are released as 0.25° apparent resolution [42]. Furthermore, the TWSA trends simulated by JPL-M indicated larger increasing and decreasing trends than those of CSR-M and GSFC-M (Table S1). A similar result was also found by Rodell et al. [1], who indicated that the 3° mascons (native resolution) of JPL-M “focus” more signals than the 1° mascons (native resolution) of CSR-M and GSFC-M over India. Additionally, the TWSA trends derived from CSR-M and JPL-M showed more spatial consistency than those from GSFC-M, especially in CC, Lake Eyre Basin (LKE), and South West Coast (SWC) (Figure 2a–c). These differences could be due to the new RL06 mascon solutions, which were applied in CSR-M and JPL-M, with a higher signal-to-noise ratio than the v02.4 mason solutions used in GSFC-M [68].
Across the entire continent of Australia, the TWSA time series derived from three different GRACE mascon solutions were highly consistent (Figure 3e); all correlation and NSE coefficients were larger than 0.90 and 0.85, respectively, and all RMSEs were lower than 1.4 cm (Table 3). Additionally, the agreement between CSR-M and JPL-M (i.e., r = 0.98, RMSE = 0.66 (cm), and NSE = 0.97) was higher than between the others (Table 3). Under extreme hydroclimatic impact, the TWSA over the continent indicated three different distinct temporal segments [16], i.e., two dry periods (i.e., 2003–2009 and 2011–2014) and one wet period (i.e., 2010–2011). Overall, the TWSA trends derived from three different GRACE mascon solutions depicted a long-period significant increasing trend in Australia throughout the full investigated period, but the TWSA trend from GSFC-M (2.38 ± 0.50 mm/year) was lower than that from CSR-M (3.69 ± 0.57 mm/year) and JPL-M (3.38 ± 0.62 mm/year).
The spatial and temporal differences in the TWSA trends among GRACE mascon solutions over Australia could be related to the different background models and data processing strategies used in said GRACE mascon solutions (Table 2). In order to reduce the influence of noise in the gravity field solutions on the evaluation of hydrological models, we used the ensemble mean of all GRACE mascon solutions-based TWSA as a reference value of TWSA [59].

3.2. Evaluation of Different Water Storage Trends from Hydrological Models

3.2.1. Total Terrestrial Water Storage Trend

Figure 4 maps the spatial distribution of seven different hydrological models-simulated TWSA trends (Figure 4a–g) and the reference values of TWSA trends (Figure 4h). Figure 5 shows the time series of the regional and the continental average TWSA simulations from seven different hydrological models and the corresponding reference values (i.e., the ensemble means of CSR-M, JPL-M, and GSFC-M). As shown in Figure 4 and Figure 5, all models underestimated the increasing or decreasing trends in Australia compared to GRACE, except for CLM-4.5 model. For instance, Noah-3.6 and VIC-4.1.2 models indicated significant wetting TWSA trends in MDB (Figure 4a,c and Figure 5c) with a value of 5.37 ± 0.79 mm/year and 4.04 ± 0.68 mm/year, respectively. However, these values are lower than the reference value of 7.67 ± 0.83 mm/year. Additionally, these models showed no obvious wetting TWSA trends in CC and NEC (Figure 5a,b and Tables S2 and S3) and drying trends in the NWP (Figure 5d and Table S5). Furthermore, despite CLSM-F2.5, WaterGAP-2.2d, PCR-GLOBWB-2, and AWRA-L v6 models containing all water storage compartments, these models also showed an underestimation of the TWSA trends compared to GRACE, in particular, the increasing trends in CC (Figure 5a and Table S2) and the decreasing trends in NWP (Figure 5d and Table S5). On the contrary, CLM-4.5 model overestimated the increasing trends in NEC (28.62 ± 1.28 mm/year) compared to the reference value of 7.66 ± 0.81 mm/year (Figure 5b). Additionally, we found that although WaterGAP-2.2d was the only model used in this study that considers human water use and calibration (Table 1), it showed lower TWSA trends and more non-significant trends than the other models (Figure 4d and Tables S2–S5).
Across the entire continent of Australia, all of the hydrological models indicated similar TWSA temporal changes to those of reference value (Table 4). CLM-4.5 model presented the highest agreement (r = 0.95, RMSE = 1.05 cm, and NSE = 0.91) in terms of TWSA to the reference value, whereas WaterGAP-2.2d model expressed the lowest agreement (r = 0.77, RMSE = 3.02 cm, and NSE = 0.20). Additionally, except for CLM-4.5 model, the TWSA trends from all models (ranging from 0.56 ± 0.13 to 2.02 ± 0.45 mm/year) (Table 5) were lower than that of the reference value, with a rate of 3.15 ± 0.56 mm/year. Furthermore, although CLM-4.5 model demonstrated the closest agreement with GRACE, this model overestimates the GRACE-derived rising TWSA trend, with a rate of 3.79 ± 0.52 mm/year. In addition, we observed that there were large discrepancies in TWSA between GRACE and hydrological models over the period of 2011–2013; these discrepancies may be due to the hydrological models underestimating the process of severe flooding caused by the strongest La Niña event on record in Australia [15].
The differences in TWSA trends may be due to the uncertainties of GRACE and hydrological models [5]. However, we found that the standard deviations in TWSA among GRACE mascon solutions are much lower than those from hydrological models (Figure 5, Table 3 and Table 4, and Tables S6–S13). Therefore, this suggests that the uncertainties in hydrological models are the main reason for the differences in TWSA trends between GRACE and hydrological models over Australia. The main factors associated with hydrological model uncertainties include model structure, climate forcing input, consideration of human water use or not, and model calibration [3]. By comparison, the water storage components and the capacity related to model structure have the most substantial impact on a hydrological model’s uncertainties [3,5], so we focused on studying this factor.
It can be clearly seen that one of the main reasons for Noah-3.6 and VIC-4.1.2 models underestimating the GRACE-based trend is because these models do not include groundwater in their simulations (Table 1). For other models, however, we could not directly demonstrate the differences in TWSA trends between GRACE and hydrological models being caused by the uncertainties in soil moisture and/or groundwater. Therefore, it was necessary to assess the individual water storage trends derived from hydrological models.

3.2.2. Soil Moisture Storage Trend

Figure 6 shows the spatial distributions of SMSA trends simulated by seven different hydrological models (Figure 6a–g) and the reference values (Figure 6h), while Figure 7 shows the regional and continental average temporal changes in SMSA derived from these seven different hydrological models and the corresponding reference values. As shown in Figure 6a, Noah-3.6 model indicated pronounced wetting SMSA trends in NEC (2.77 ± 0.67 mm/year; Figure 7b) and MDB (5.37 ± 0.79 mm/year; Figure 7c), while non-significant drying trends in CC (−0.16 ± 0.49 mm/year; Figure 7a) and NWP (−0.13 ± 0.51 mm/year; Figure 7d). Similar patterns in these trends were observed in VIC-4.1.2, CLM-4.5, and AWRA-L v6 models (Figure 6c,f,g and Figure 7a–d, and Tables S2–S5). However, CLM-4.5 model showed higher increasing SMSA trends in NEC (9.34 ± 0.68 mm/year; Figure 7b and Table S3) and larger decreasing SMSA trends in NWP (−5.12 ± 0.43 mm/year; Figure 7d and Table S5). This could be related to the fact that the CLM-4.5 model includes a dry surface layer, which can significantly reduce the evaporation in NEC [69]; however, this dry surface layer may overestimate evaporation in NWP. In comparison, CLSM-F2.5, WaterGAP-2.2d, and PCR-GLOBWB-2 models underestimated the SMSA trends in Australia, especially the wetting SMSA trends in NEC and MDB (Figure 6b–e and Figure 7b,c and Tables S3 and S4).
For the whole continent of Australia, the SMS variations estimated by Noah-3.6, VIC-4.1.2, CLM-4.5, and AWRA-L v6 models were highly consistent with all of the correlation coefficients, and NSE coefficients were larger than 0.90, whereas all of the RMSEs were lower than 1.0 cm (Table 4). On the contrary, CLSM-F2.5, WaterGAP-2.2d, and PCR-GLOBWB-2 models showed similar SMS changes to the correlation coefficients, ranging from 0.66 to 0.95 (Table 4), whereas their changing magnitudes were lower than those from the other models with the NSE coefficients ranged from 0.17 to 0.60 and the RMSEs ranging from 1.76 to 2.54 cm (Table 4), especially in 2011 (Figure 7e).
The above results reveal that CLSM-F2.5, WaterGAP-2.2d, and PCR-GLOBWB-2 models underestimated the spatio-temporal pattern of SMSA trends. This underestimation can be explained by the fact that the soil profiles of these three models are too thin to sufficiently accommodate the soil moisture storage, e.g., most of the soil thicknesses of WaterGAP-2.2d model in Australia are approximately 0.5–1.5 m [3]. Additionally, these three models had worse performance in simulating extreme hydrological changes. To avoid possible biases in trend calculations, we applied the ensemble average of all of the hydrological models-derived SMSA as the SMSA reference values in Australia, with the exception of CLSM-F2.5, WaterGAP-2.2d, and PCR-GLOBWB-2 models.

3.2.3. Groundwater Storage Trend

The spatial patterns of GWSA trends derived from five different models and the corresponding reference values are displayed in Figure 8, while the temporal variations of the regional and the continental average GWSA simulations from five different hydrological models and the corresponding references value are shown in Figure 9. Distinct spatial differences in the GWSA trends among five different models can be observed (Figure 8a–e). These differences imply that it may be unreasonable to selected one model or a multi-model ensemble mean as a reference value. Therefore, the residuals between the reference values of TWSA trends (the ensemble means of CSR-M, JPL-M, and GSFC-M) and the reference values of SMSA trends (the ensemble mean of Noah-3.6, VIC-4.1.2, CLM-4.5, and AWRA-L v6 models) were applied as the reference values of GWSA trends. This hypothesis is consistent with the previous studies [40,51]. As shown in Figure 8f, the reference values of GWSA indicated significant increasing trends in CC (7.09 ± 0.51 mm/year; Figure 9a), NEC (6.45 ± 0.31 mm/year; Figure 9b) and MDB (3.56 ± 0.41 mm/year; Figure 9c), whereas pronounced decreasing trends in NWP (−5.55 ± 0.31 mm/year; Figure 9b). All of the hydrological models, with the exception of CLM-4.5 model, underestimated the reference values of GWSA trends (Figure 8a–c,e and Tables S2–S5). This means that these four models lack sufficient capacity to catch the groundwater storage variations in Australia. By comparison, CLM-4.5 model indicated larger pronounced positive or negative GWSA trends than those of the reference values (Figure 8d), especially in NEC (19.28 ± 0.83 mm/year compared to the reference value of 6.45 ± 0.31 mm/year, Figure 9b) and MDB (−0.67 ± 0.46 mm/year compared with the reference value of 3.56 ± 0.41 mm/year, Figure 9d). Swenson and Lawrence [21] attributed this overestimation to CLM-4.5 model lacking a finite lower boundary in the bulk aquifer model.
It should be pointed out that poor modeling of the influence of ocean tides and non-tide ocean mass movement can affect the GRACE water storage estimates in the nearby Gulf of Carpentaria [20,70]. However, these errors introduce a cyclical error without affecting long-term trends [40]. Additionally, a lower aquifer indicates an obvious rising groundwater level trend during 2004–2014 in the northern part of Australia from the Australian Groundwater Insight [71]. Hence, the increasing GWSA trends from the reference values in the northern part of Australia are reliable (Figure 8f). However, all of the hydrological models underestimated these increasing trends (Figure 8a–e), which could be attributed to the fact that these increasing trends are mostly expressed as GWSA trends of the lower aquifer, and all of the hydrological models may lack sufficient storage capacity to accommodate variations in deep groundwater [21].
In general, under the impact of “big wet” driven by one of the strongest La Niña events in 2011 [16], all of the hydrological models indicated a significantly increasing GWSA trend for the whole continent of Australia during the study period (Table 5). However, the GWSA trends derived from CLSM-F2.5, WaterGAP-2.2d, PCR-GLOBWB-2, and AWRA-L v6 models (ranging from 0.28 ± 0.08 to 1.04 ± 0.44 mm/year) were lower than that of the reference value (with a trend of 1.57 ± 0.32 mm/year). On the contrary, CLM-4.5 model demonstrated good agreement (r = 0.80, RMSE = 0.90 cm, and NSE = 0.63) in GWS variations with the reference values, but it is likely to overestimate GWSA trend (with a trend of 2.53 ± 0.20 mm/year). In addition, CLSM-F2.5 model indicated the highest GWSA bias out of all the other models (Figure 9a–e and Table 4). This could be related to the soil thickness of CLSM-F2.5 model being only 1 m, thus resulting in larger changes in GWSA [24]. Therefore, the depth of the soil layer has a significant influence on groundwater storage variations [21]; however, the manner in which soil thickness affects groundwater storage was beyond the scope of this paper.

3.3. Influence of Model Structure on Model Uncertainty

Based on the aforementioned results presented in Section 3.1 and Section 3.2, different water storage changes in Australia can be calculated through a comprehensive synergy of GRACE mascon solutions and hydrological model simulations. The pronounced decreasing TWSA trends were located in NWP and mainly expressed as a decline in GWSA trends (Figure 4h and Figure 8f), which may be associated with the influence of Pilbara’s mining industry [1]. On the contrary, significant increasing TWSA trends were found in CC, NEC, and MDB (Figure 4h), which are attributed to the impact of a heavy rain event in 2011 [16]. The trends in NEC and MDB were expressed as wetting SMSA and GWSA trends (Figure 4h, Figure 6h, and Figure 8f), whereas the trends in CC were mostly indicated as increasing GWSA trends (Figure 4h, Figure 6h, and Figure 8f). In summary, SMSA trends demonstrated similar contributions (50.16 ± 15.24%) to TWSA trends than those from GWSA trends (49.84% ± 10.16%) in Australia over the period of 2003–2014 (Table 5).
As shown in Figure 10 and Table 5, all of the hydrological models underestimated the GRACE-derived increasing TWSA trends in Australia, with the exception of CLM-4.5 model. The causes for the underestimation can be divided into three categories: (1) the model ignores the groundwater water component, i.e., Noah-3.6 and VIC-4.12 models [5]; (2) the model’s soil depth is too small to accommodate the range in soil moisture change and lacks sufficient groundwater storage capacity, i.e., CLSM-F2.5, WaterGAP-2.2d, and PCR-GLOBWB-2 models [5]; (3) the model does not have enough ability to catch groundwater storage changes, i.e., AWRA-L v6 model [20]. On the contrary, CLM-4.5 model overestimated the GRACE-based TWSA trends because of the overestimation of GWSA trends, which was induced by the lack of a finite lower boundary in the bulk aquifer, with poor responses to large wetting events [21]. Besides the trend in TWSA, the seasonal and inter-annual variability in TWSA can also be selected as evaluation metrics to assess the performance of hydrological models [23,54]. These two metrics will be studied in the future.

3.4. Impact of Other Factors on Model Uncertainty

In addition to the model structure, the differences in TWSA trends between GRACE and hydrological models were also affected by climate forcing, consideration of human water use or not, and model calibration [3,5].

3.4.1. Climate Forcing

Using different climate forcing in seven different models may be a disadvantage in this study. However, it is very difficult to apply the same climate forcing for all hydrological models in order to isolate the influence of climate forcing since some models are not in operational mode (e.g., WaterGAP-2.2d) [3]. To easily evaluate the impact of different forcing data on the conclusion of this study, we made a comparison among three common GLDAS models, i.e., Noah model in GLDAS-2.0 and GLDAS-2.1 and CLSM model in GLDAS-2.1. GLDAS-2.0 is forced with the updated Princeton meteorological forcing data (V2.2), while GLDAS-2.1 is forced with the National Oceanic and Atmospheric Administration (NOAA)/Global Data Assimilation System (GDAS) atmospheric analysis fields, the disaggregated Global Precipitation Climatology Project (GPCP) V1.3 Daily Analysis precipitation fields, and the Air Force Weather Agency’s AGRicultural METeorological modeling system (AGRMET) radiation fields (more detail can be found in README for NASA GLDAS Version 2 Data). Moreover, the soil thickness of Noah model is 2.0 m, while it is only 1.0 m for CLSM model. In other words, Noah model in GLDAS-2.0 has the same model structure but different climate forcing to Noah model in GLDAS-2.1, whereas CLSM model in GLDAS-2.1 indicates uniform forcing input data but a different model structure to Noah model in GLDAS-2.1. Therefore, these three models provide us a good opportunity to compare the influence of different climate forcing and different model structures on model uncertainty.
As can be seen in Figure 11a,b, two different Noah models showed similar spatial distribution, i.e., decreasing SMSA trends in NWP and increasing SMSA trends in MDB. However, Noah model in GLDAS-2.0 states larger drying SMSA trends in NWP (−2.36 ± 0.44 mm/year) and lower wetting SMSA trends in MDB (3.27 ± 0.73 mm/year) than those of Noah model in GLDAS-2.1 (−0.13 ± 0.51 mm/year and 5.37 ± 0.79 mm/year in NWP and MDB, respectively), which could be related to the different climate forcing used in these two models. In comparison, CLSM model indicated no obvious decreasing SMSA trends in NWP (−0.04 ± 0.13 mm/year) and lower increasing SMSA trends in MDB (0.85±0.15 mm/year, Figure 11c). Across the whole continent of Australia, two different Noah models presented generally good agreement (r = 0.98, RMSE = 0.73 cm, and NSE = 0.94) in SMS variations during the entire period (Figure 12), except that large discrepancies in SMSA were found from 2011 to 2012, which were caused by a strong precipitation event in 2011. On the contrary, the magnitude of the SMS changes from CLSM model were always lower than those of the two Noah models, and the agreement metrics between CLSM model and Noah-3.6 model (r = 0.94, RMSE = 2.44 cm, and NSE = 0.37) were lower than those of between two different Noah models. Furthermore, these three GLDAS models indicate increasing SMSA trends over the whole study period, but the increasing magnitude revealed by CLSM model (with a slope of 0.25 ± 0.12 mm/year) was much lower than that of the two different Noah models (with rates of 1.35 ± 0.36 and 1.74 ± 0.46 mm/year in GLDAS-2.0 and GLDAS-2.1, respectively). In summary, model structure and climate forcing can result in differences in TWSA trends between GRACE and hydrological models, but the impact of the model structure on these differences is much greater than that of climate forcing. These results are supported by the findings of Scanlon et al. [5], who also identified that the influence of model structure on TWSA trends is stronger than climate forcing by using different climate forcing into WaterGAP model and applying the same climate forcing to WaterGAP and PCR-GLOBWB models. Therefore, although different climate forcing in models leads to the differences in TWSA trends between GRACE and hydrological models, the conclusion in this study based on model structure is reasonable.

3.4.2. Human Water Use and Model Calibration

It is interesting to note that although WaterGAP-2.2d model was the only model applied in the current study that considers human water use and model calibration (Table 1), it showed the worst agreement in terms of TWSA with GRACE relative to the other hydrological models (Table 4). On the contrary, CLM-4.5 model does not consider human water use and model calibration, yet showed the best agreement in terms of TWSA with GRACE (Table 4). Therefore, this implies that the factors of human water use and model calibration may have uncertainties or are unlikely to be the main cause of the differences in TWSA trends between GRACE and hydrological models in Australia for the period of 2003–2014 [5]. It should be pointed out that human water use can be a primary reason for groundwater depletion in some Australian regions (e.g., in Victoria [12] and south-west western Australia [72]); however, in the current study, we focused on evaluating the performance of hydrological models over the whole continent of Australia; hence, human water use and model calibration did not influence our conclusions.
Overall, we emphasize that model structure is the most important cause for discrepancies in TWSA between GRACE and hydrological models, and do not deny that other factors also have an impact; however, these influences on the conclusions of this study can be ignored.

4. Conclusions

Assessment of a hydrological model’s performance is important for managing water resources and for guiding its future improvement. In this study, we applied three newly available GRACE mascon solutions (i.e., CSR-M, JPL-M, and GSFC-M) to evaluate the spatio-temporal performance of seven widely used hydrological models (i.e., Noah-3.6, CLSM-F2.5, VIC-4.1.2, WaterGAP-2.2d, PCR-GLOBWB-2, CLM-4.5, and AWRA-L v6 models) over Australia from 2003 to 2014. The spatio-temporal differences in TWSA trends between GRACE and hydrological models were investigated and, more importantly, the corresponding individual water storage components (i.e., SMSA and GWSA) that lead to the differences in TWSA trends were explored.
Although different background models and data processing strategies were used in CSR-M, JPL-M and GSFC-M, high spatio-temporal agreement in TWSA was found between them. Additionally, the standard deviations among three GRACE mascon solutions-derived TWSA were lower than that among hydrological models. Therefore, GRACE mascon solutions can be used as valuable data to assist in the improvement of hydrological models.
The Australian TWSA was mainly composed of SMSA and GWSA. The TWSA trends showed a bipolar pattern, i.e., increasing trends in CC, NEC, and MDB, and decreasing TWSA trends in NWP. However, the increasing TWSA trends in CC and the decreasing TWSA trends in NWP were mostly due to groundwater storage variations, while the increasing TWSA trends in NEC and MDB were attributed to changes in both soil moisture and groundwater storage. Across the whole continent of Australia, the TWSA trend indicated a pronounced increasing trend with a value of 3.15 ± 0.56 mm/year throughout the full investigated period. The contributions of SMSA trend (1.58 ± 0.48 mm/year) and GWSA trend (1.57 ± 0.32 mm/year) to TWSA trend were similar, 50.16 ± 15.24% and 49.84% ± 10.16%, respectively.
The differences in TWSA trends between GRACE and hydrological models were mainly caused by uncertainties in these hydrological models. The influences of four different driving forces (i.e., model structure, climate forcing input, consideration of human water use or not, and model calibration) on hydrological models’ uncertainties were analyzed. Model structure was the most important reason; climate forcing can result in differences in TWSA trends between GRACE and hydrological models, but the impact of climate forcing on these differences was much lower than that of model structure. Additionally, the factors of human water use and model calibration may have uncertainties or were unlikely to be the main cause of the differences in TWSA trends between GRACE and hydrological models in Australia for the period of 2003–2014.
All of the hydrological models applied in this study, except for CLM-4.5 model, underestimated the GRACE-derived TWSA trends over the whole continent of Australia. Different hydrological models showed different causes for the differences in TWSA trends between them and GRACE. We can divide the causes of underestimation into three categories: missing groundwater storage component (for Noah-3.6 and VIC-4.1.2 models), lack of sufficient capacity to accommodate the range in soil moisture and groundwater storage trends (for CLSM-F2.5, WaterGAP-2.2d, and PCR-GLOBWB-2 models), and inadequate ability to catch groundwater storage changes (for AWRA-L v6 model). In contrast, CLM-4.5 model indicated the best agreement with GRACE TWSA, but overestimated the GRACE-derived TWSA trends, mostly due to the overestimation of GWSA trends.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/12/21/3578/s1, Table S1: Statistical summary of TWSA trends (mm/year) derived from three different GRACE mascon solutions in regions (Carpentaria Coast (CC), North East Coast (NEC), Murray-Darling Basin (MDB), and North Western Plateau (NWP)), and the whole continent of Australia; Table S2: Statistical summary of different water storage trends (mm/year) derived from hydrological models and reference values in CC from 2003 to 2014; Table S3: Statistical summary of different water storage trends (mm/year) derived from hydrological models and reference values in NEC from 2003 to 2014; Table S4: Statistical summary of different water storage trends (mm/year) derived from hydrological models and reference values in MDB from 2003 to 2014; Table S5: Statistical summary of different water storage trends (mm/year) derived from hydrological models and reference values in NWP from 2003 to 2014; Table S6: Statistical summary of temporal agreement metrics between GRACE mason solutions in CC; Table S7: Statistical summary of temporal agreement metrics between GRACE mason solutions in NEC; Table S8: Statistical summary of temporal agreement metrics between GRACE mason solutions in MDB; Table S9: Statistical summary of temporal agreement metrics between GRACE mason solutions in NWP; Table S10: Statistical summary of agreement metrics between reference values and hydrological models in CC; Table S11: Statistical summary of agreement metrics between reference values and hydrological models in NEC; Table S12: Statistical summary of agreement metrics between reference values and hydrological models in MDB; Table S13: Statistical summary of agreement metrics between reference values and hydrological models in NWP.

Author Contributions

Conceptualization, X.Y. and S.T.; funding acquisition, W.Y.; methodology, X.Y.; software, X.Y.; supervision, W.Y.; visualization, X.Y.; writing—original draft, X.Y.; writing—review and editing, S.T., W.F., J.R., W.Y., Z.J. and X.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (grant no. 41974013).

Acknowledgments

The authors appreciate Thedini Asali Peiris (e-mail: [email protected]) for providing the WaterGAP-2.2d output, Edwin H. Sutanudjaja ([email protected]) for providing PCR-GLOBWB-2 output, and Keith Oleson ([email protected]) for providing CLM-4.5 output for this study. GLDAS output is available at the Goddard Earth Sciences Data and Information Services Center, NASA [73]. CSR GRACE RL06 mascon solutions v01 are available at the Center for Space Research at The University of Texas at Austin [41]; JPL GRACE RL06 mascon solutions v01 are available at the Jet Propulsion Laboratory website [74]; GSFC mascon solutions v02.4 are available at Goddard Earth Science Laboratories website [75].

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef] [PubMed]
  2. Bierkens, M.F.P. Global hydrology 2015: State, trends, and directions. Water Resour. Res. 2015, 51, 4923–4947. [Google Scholar] [CrossRef]
  3. Müller Schmied, H.; Eisner, S.; Franz, D.; Wattenbach, M.; Portmann, F.T.; Flörke, M.; Döll, P. Sensitivity of simulated global-scale freshwater fluxes and storages to input data, hydrological model structure, human water use and calibration. Hydrol. Earth Syst. Sci. 2014, 18, 3511–3538. [Google Scholar] [CrossRef] [Green Version]
  4. Oleson, K.W.; Lawrence, D.M.; Bonan, G.B.; Flanner, M.G.; Kluzek, E.; Lawrence, P.J.; Levis, S.; Swenson, S.C.; Thornton, P.E.; Dai, M.A.; et al. Technical Description of Version 4.0 of the Community Land Model (CLM); NCAR Technical Note NCAR/TN-478+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2010; 257p. [Google Scholar]
  5. Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Muller Schmied, H.; van Beek, L.P.H.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C.; et al. Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  6. Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  7. Leblanc, M.J.; Tregoning, P.; Ramillien, G.; Tweed, S.O.; Fakes, A. Basin-scale, integrated observations of the early 21st century multiyear drought in southeast Australia. Water Resour. Res. 2009, 45, W04408. [Google Scholar] [CrossRef]
  8. Chiew, F.H.S.; Young, W.J.; Cai, W.; Teng, J. Current drought and future hydroclimate projections in southeast Australia and implications for water resources management. Stoch. Environ. Res. Risk Assess. 2010, 25, 601–612. [Google Scholar] [CrossRef]
  9. McGrath, G.S.; Sadler, R.; Fleming, K.; Tregoning, P.; Hinz, C.; Veneklaas, E.J. Tropical cyclones and the ecohydrology of Australia’s recent continental-scale drought. Geophys. Res. Lett. 2012, 39, L03404. [Google Scholar] [CrossRef] [Green Version]
  10. van Dijk, A.I.J.M.; Beck, H.E.; Crosbie, R.S.; de Jeu, R.A.M.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The Millennium Drought in southeast Australia (2001-2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
  11. Zhao, M.A.G.; Velicogna, I.; Kimball, J.S. A Global Gridded Dataset of GRACE Drought Severity Index for 2002–14: Comparison with PDSI and SPEI and a Case Study of the Australia Millennium Drought. J. Hydrometeorol. 2017, 18, 2117–2129. [Google Scholar] [CrossRef] [Green Version]
  12. Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Scanlon, B.; Güntner, A. Long-term groundwater storage change in Victoria, Australia from satellite gravity and in situ observations. Glob. Planet. Chang. 2016, 139, 56–65. [Google Scholar] [CrossRef] [Green Version]
  13. Yan, J.; Jia, S.; Lv, A.; Mahmood, R.; Zhu, W. Analysis of the spatio-temporal variability of terrestrial water storage in the Great Artesian Basin, Australia. Water Sci. Technol. Water Suppl. 2017, 17, 324–341. [Google Scholar] [CrossRef]
  14. García-García, D.; Ummenhofer, C.C.; Zlotnicki, V. Australian water mass variations from GRACE data linked to Indo-Pacific climate variability. Remote Sens. Environ. 2011, 115, 2175–2183. [Google Scholar] [CrossRef] [Green Version]
  15. Fasullo, J.T.; Boening, C.; Landerer, F.W.; Nerem, R.S. Australia’s unique influence on global sea level in 2010–2011. Geophys. Res. Lett. 2013, 40, 4368–4373. [Google Scholar] [CrossRef]
  16. Xie, Z.; Huete, A.; Restrepo-Coupe, N.; Ma, X.; Devadas, R.; Caprarelli, G. Spatial partitioning and temporal evolution of Australia’s total water storage under extreme hydroclimatic impacts. Remote Sens. Environ. 2016, 183, 43–52. [Google Scholar] [CrossRef]
  17. Xie, Z.; Huete, A.; Cleverly, J.; Phinn, S.; McDonald-Madden, E.; Cao, Y.; Qin, F. Multi-climate mode interactions drive hydrological and vegetation responses to hydroclimatic extremes in Australia. Remote Sens. Environ. 2019, 231, 111270. [Google Scholar] [CrossRef]
  18. Vishwakarma, B.; Devaraju, B.; Sneeuw, N. What Is the Spatial Resolution of grace Satellite Products for Hydrology? Remote Sens. 2018, 10, 852. [Google Scholar] [CrossRef] [Green Version]
  19. Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 5, 358–369. [Google Scholar] [CrossRef]
  20. van Dijk, A.I.J.M.; Renzullo, L.J.; Rodell, M. Use of Gravity Recovery and Climate Experiment terrestrial water storage retrievals to evaluate model estimates by the Australian water resources assessment system. Water Resour. Res. 2011, 47, W11524. [Google Scholar] [CrossRef]
  21. Swenson, S.C.; Lawrence, D.M. A GRACE-based assessment of interannual groundwater dynamics in the Community Land Model. Water Resour. Res. 2015, 51, 8817–8833. [Google Scholar] [CrossRef]
  22. Tangdamrongsub, N.; Han, S.-C.; Tian, S.; Müller Schmied, H.; Sutanudjaja, E.H.; Ran, J.; Feng, W. Evaluation of Groundwater Storage Variations Estimated from GRACE Data Assimilation and State-of-the-Art Land Surface Models in Australia and the North China Plain. Remote Sens. 2018, 10, 483. [Google Scholar] [CrossRef] [Green Version]
  23. Scanlon, B.R.; Zhang, Z.; Rateb, A.; Sun, A.; Wiese, D.; Save, H.; Beaudoing, H.; Lo, M.H.; Müller-Schmied, H.; Döll, P.; et al. Tracking Seasonal Fluctuations in Land Water Storage Using Global Models and GRACE Satellites. Geophys. Res. Lett. 2019, 46, 5254–5264. [Google Scholar] [CrossRef]
  24. Xia, Y.; Mocko, D.; Huang, M.; Li, B.; Rodell, M.; Mitchell, K.E.; Cai, X.; Ek, M.B. Comparison and Assessment of Three Advanced Land Surface Models in Simulating Terrestrial Water Storage Components over the United States. J. Hydrometeorol. 2017, 18, 625–649. [Google Scholar] [CrossRef]
  25. Bureau of Meteorology, Australian Government. Australian Hydrological Geospatial Fabric (Geofabric). Available online: http://www.bom.gov.au/water/geofabric/inuse.shtml (accessed on 22 February 2020).
  26. Awange, J.L.; Sharifi, M.A.; Baur, O.; Keller, W.; Featherstone, W.E.; Kuhn, M. GRACE hydrological monitoring of Australia: Current limitations and future prospects. J. Spat. Sci. 2009, 54, 23–36. [Google Scholar] [CrossRef]
  27. Brown, N.J.; Tregoning, P. Quantifying GRACE data contamination effects on hydrological analysis in the Murray–Darling Basin, southeast Australia. Aust. J. Earth Sci. 2010, 57, 329–335. [Google Scholar] [CrossRef] [Green Version]
  28. Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
  29. Gupta, S.K. Modern Hydrology and Sustainable Water Development; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
  30. Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
  31. Sutanudjaja, E.H.; van Beek, R.; Wanders, N.; Wada, Y.; Bosmans, J.H.C.; Drost, N.; van der Ent, R.J.; de Graaf, I.E.M.; Hoch, J.M.; de Jong, K.; et al. PCR-GLOBWB 2: A 5 arcmin thinsp;arcmin global hydrological and water resources model. Geosci. Model Dev. 2018, 11, 2429–2453. [Google Scholar] [CrossRef] [Green Version]
  32. Oleson, K.W.; Lawrence, D.M.; Bonan, G.B.; Drewniak, B.; Huang, M.; Koven, C.D.; Levis, S.; Li, F.; Riley, W.J.; Subin, Z.M.; et al. Technical Description of Version 4.5 of the Community Land Model (CLM) NCAR Technical Note NCAR/TNG 503+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2013; p. 420. [Google Scholar]
  33. Frost, A.J.; Ramchurn, A.; Smith, A. The Australian Landscape Water Balance Model. (AWRA-L v6). Technical Description of the Australian Water Resources Assessment Landscape Model, 6th ed.; Technical Report; The Bureau of Meteorology: Melbourne, Australia, 2018.
  34. NASA Land Data Assimilation System. GLDAS Specifications. Available online: https://ldas.gsfc.nasa.gov/sites/default/files/ldas/gldas/SOILS/GLDASp5_vicsoildp_10d.nc4 (accessed on 22 February 2020).
  35. Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Grand, S. GRACE detects coseismic and postseismic deformation from the Sumatra-Andaman earthquake. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
  36. van Dam, T.; Wahr, J.; Lavallée, D. A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
  37. Ivins, E.R.; Watkins, M.M.; Yuan, D.-N.; Dietrich, R.; Casassa, G.; Rülke, A. On-land ice loss and glacial isostatic adjustment at the Drake Passage: 2003–2009. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
  38. Chambers, D.P.; Cazenave, A.; Champollion, N.; Dieng, H.; Llovel, W.; Forsberg, R.; von Schuckmann, K.; Wada, Y. Evaluation of the Global Mean Sea Level Budget between 1993 and 2014. Surv. Geophys. 2016, 38, 309–327. [Google Scholar] [CrossRef]
  39. Rieser, D.; Kuhn, M.; Pail, R.; Anjasmara, I.M.; Awange, J. Relation between GRACE-derived surface mass variations and precipitation over Australia. Aust. J. Earth Sci. 2010, 57, 887–900. [Google Scholar] [CrossRef]
  40. Tregoning, P.; McClusky, S.; Van Dijk, A.I.J.M.; Crosbie, R.S.; Peña-Arancibia, J.L. Assessment of GRACE Satellites for Groundwater Estimation in Australia; Waterlines report; National Water Commission: Canberra, Australia, 2012; p. 82. [Google Scholar]
  41. Save, H. “CSR GRACE RL06 Mascon Solutions”, Texas Data Repository Dataverse, V1. 2019. Available online: https://dataverse.tdl.org/dataset.xhtml;jsessionid=505699c57eee01fc06638c10a1a6?persistentId=doi%3A10.18738%2FT8%2FUN91VR&version=&q=&fileTypeGroupFacet=%22Data%22&fileAccess=&fileSortField=date (accessed on 5 February 2020).
  42. Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
  43. Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
  44. Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
  45. Luthcke, S.B.; Sabaka, T.J.; Loomis, B.D.; Arendt, A.A.; McCarthy, J.J.; Camp, J. Antarctica, Greenland and Gulf of Alaska land-ice evolution from an iterated GRACE global mascon solution. J. Glaciol. 2013, 59, 613–631. [Google Scholar] [CrossRef]
  46. Forootan, E.; Awange, J.L.; Kusche, J.; Heck, B.; Eicker, A. Independent patterns of water mass anomalies over Australia from satellite data and models. Remote Sens. Environ. 2012, 124, 427–443. [Google Scholar] [CrossRef] [Green Version]
  47. Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113, B08410. [Google Scholar] [CrossRef] [Green Version]
  48. Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
  49. Rodell, M.; Chao, B.F.; Au, A.Y.; Kimball, J.S.; McDonald, K.C. Global biomass variation and its geodynamic effects. Earth Interact. 2005, 9, 1–19. [Google Scholar] [CrossRef] [Green Version]
  50. Getirana, A.; Kumar, S.; Girotto, M.; Rodell, M. Rivers and Floodplains as Key Components of Global Terrestrial Water Storage Variability. Geophys. Res. Lett. 2017, 44, 10359–10368. [Google Scholar] [CrossRef] [Green Version]
  51. Wang, J.; Song, C.; Reager, J.T.; Yao, F.; Famiglietti, J.S.; Sheng, Y.; MacDonald, G.M.; Brun, F.; Schmied, H.M.; Marston, R.A.; et al. Recent global decline in endorheic basin water storages. Nat. Geosci. 2018, 11, 926–932. [Google Scholar] [CrossRef] [Green Version]
  52. Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
  53. Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. Assessing Global Water Storage Variability from GRACE: Trends, Seasonal Cycle, Subseasonal Anomalies and Extremes. Surv. Geophys. 2016, 37, 357–395. [Google Scholar] [CrossRef] [Green Version]
  54. Long, D.; Pan, Y.; Zhou, J.; Chen, Y.; Hou, X.; Hong, Y.; Scanlon, B.R.; Longuevergne, L. Global analysis of spatiotemporal variability in merged total water storage changes using multiple GRACE products and global hydrological models. Remote Sens. Environ. 2017, 192, 198–216. [Google Scholar] [CrossRef]
  55. Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
  56. Kendall, M.G. Rand Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
  57. Wang, F.; Shao, W.; Yu, H.; Kan, G.; He, X.; Zhang, D.; Ren, M.; Wang, G. Re-evaluation of the Power of the Mann-Kendall Test for Detecting Monotonic Trends in Hydrometeorological Time Series. Front. Earth Sci. 2020, 8, 14. [Google Scholar] [CrossRef]
  58. Hamed, K.H. Trend detection in hydrologic data: The Mann–Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
  59. Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
  60. Holgate, C.M.; De Jeu, R.A.M.; van Dijk, A.I.J.M.; Liu, Y.Y.; Renzullo, L.J.; Vinodkumar; Dharssi, I.; Parinussa, R.M.; Van Der Schalie, R.; Gevaert, A.; et al. Comparison of remotely sensed and modelled soil moisture data sets across Australia. Remote Sens. Environ. 2016, 186, 479–500. [Google Scholar] [CrossRef]
  61. Tian, S.; Tregoning, P.; Renzullo, L.J.; van Dijk, A.I.J.M.; Walker, J.P.; Pauwels, V.R.N.; Allgeyer, S. Improved water balance component estimates through joint assimilation of GRACE water storage and SMOS soil moisture retrievals. Water Resour. Res. 2017, 53, 1820–1840. [Google Scholar] [CrossRef]
  62. Kerr, Y.H.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS performance in terms of global soil moisture monitoring after six years in operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
  63. Leblanc, M.; Tweed, S.; Van Dijk, A.; Timbal, B. A review of historic and future hydrological changes in the Murray-Darling Basin. Glob. Planet. Chang. 2012, 80–81, 226–246. [Google Scholar] [CrossRef]
  64. Bureau of Meteorology, Australian Government. Australian Groundwater Insight. Available online: http://www.bom.gov.au/water/groundwater/insight/#/bore/density (accessed on 15 June 2020).
  65. Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; de Linage, C.R.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38, L03403. [Google Scholar] [CrossRef] [Green Version]
  66. Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  67. Tangdamrongsub, N.; Han, S.-C.; Decker, M.; Yeo, I.-Y.; Kim, H. On the use of the GRACE normal equation of inter-satellite tracking data for estimation of soil moisture and groundwater in Australia. Hydrol. Earth Syst. Sci. 2018, 22, 1811–1829. [Google Scholar] [CrossRef] [Green Version]
  68. Göttl, F.; Schmidt, M.; Seitz, F. Mass-related excitation of polar motion: An assessment of the new RL06 GRACE gravity field models. Earth Planets Space 2018, 70, 195. [Google Scholar] [CrossRef]
  69. Swenson, S.C.; Lawrence, D.M. Assessing a dry surface layer-based soil resistance parameterization for the Community Land Model using GRACE and FLUXNET-MTE data. J. Geophys. Res. Atmos. 2014, 119, 10299–10312. [Google Scholar] [CrossRef]
  70. Tregoning, P.; Lambeck, K.; Ramillien, G. GRACE estimates of sea surface height anomalies in the Gulf of Carpentaria, Australia. Earth Planet. Sci. Lett. 2008, 271, 241–244. [Google Scholar] [CrossRef]
  71. Bureau of Meteorology, Australian Government. Australian Groundwater Insight. Available online: http://www.bom.gov.au/water/groundwater/insight/#/gwtrend/10yeartrend/lower_2014 (accessed on 20 June 2020).
  72. Hu, K.X.; Awange, J.L.; Kuhn, M.; Saleem, A. Spatio-temporal groundwater variations associated with climatic and anthropogenic impacts in South-West Western Australia. Sci. Total Environ. 2019, 696, 133599. [Google Scholar] [CrossRef] [PubMed]
  73. Goddard Earth Sciences Data and Information Services Center (GES DISC), NASA. Available online: https://disc.gsfc.nasa.gov/datasets?keywords=GLDAS (accessed on 22 February 2020).
  74. Physical Oceanography Distributed Active Archive Center, Jet Propulsion Laboratory, NASA. Available online: http://grace.jpl.nasa.gov/data/get-data/jpl_global_mascons/ (accessed on 7 February 2020).
  75. Goddard Earth Science Research, NASA. Available online: https://earth.gsfc.nasa.gov/index.php/geo/data/grace-mascons (accessed on 10 February 2020).
Remotesensing 12 03578 g001 550
Figure 1. Geographic location of the Australian continent and topographic drainage divisions.
Figure 1. Geographic location of the Australian continent and topographic drainage divisions.
Remotesensing 12 03578 g001
Remotesensing 12 03578 g002 550
Figure 2. Comparison of total terrestrial water storage anomaly (TWSA) trends over Australia (January 2003–December 2014) from Center for Space Research release 06 (RL 06) mascon solutions v01 (CSR-M) (a), Jet Propulsion Laboratory RL06 mascon solutions v01 (JPL-M) (b), and Goddard Space Flight Center mascon solutions v02.4 (GSFC-M) (c). The gray stippling indicates regions without significant trends (p ≥ 0.05).
Figure 2. Comparison of total terrestrial water storage anomaly (TWSA) trends over Australia (January 2003–December 2014) from Center for Space Research release 06 (RL 06) mascon solutions v01 (CSR-M) (a), Jet Propulsion Laboratory RL06 mascon solutions v01 (JPL-M) (b), and Goddard Space Flight Center mascon solutions v02.4 (GSFC-M) (c). The gray stippling indicates regions without significant trends (p ≥ 0.05).
Remotesensing 12 03578 g002
Remotesensing 12 03578 g003 550
Figure 3. Time series of TWSA from three different GRACE mascon solutions in Carpentaria Coast (CC) (a), North East Coast (NEC) (b), Murray–Darling Basin (MDB) (c), North Western Plateau (NWP) (d), and the whole continent of Australia (e).
Figure 3. Time series of TWSA from three different GRACE mascon solutions in Carpentaria Coast (CC) (a), North East Coast (NEC) (b), Murray–Darling Basin (MDB) (c), North Western Plateau (NWP) (d), and the whole continent of Australia (e).
Remotesensing 12 03578 g003
Remotesensing 12 03578 g004 550
Figure 4. Spatial patterns of TWSA trends over Australia from seven different hydrological models (i.e., Noah-3.6 (a); Catchment Land Surface Model (CLSM-F2.5) (b); Variable Infiltration Capacity macroscale model (VIC-4.1.2) (c); Water-Global Assessment and Prognosis (WaterGAP-2.2d) (d); PCRaster Global Water Balance (PCR-GLOBWB-2) (e); Community Land Model (CLM-4.5) (f); and Australian Water Resources Assessment Landscape model (AWRA-L v6) (g)) and the corresponding reference values (h) for the period of January 2003–December 2014. The reference values of TWSA trends are shown as the ensemble means of three different GRACE mascon solutions (i.e., CSR-M, JPL-M, and GSFC-M). The gray stippling indicates regions with non-significant trends (p ≥ 0.05).
Figure 4. Spatial patterns of TWSA trends over Australia from seven different hydrological models (i.e., Noah-3.6 (a); Catchment Land Surface Model (CLSM-F2.5) (b); Variable Infiltration Capacity macroscale model (VIC-4.1.2) (c); Water-Global Assessment and Prognosis (WaterGAP-2.2d) (d); PCRaster Global Water Balance (PCR-GLOBWB-2) (e); Community Land Model (CLM-4.5) (f); and Australian Water Resources Assessment Landscape model (AWRA-L v6) (g)) and the corresponding reference values (h) for the period of January 2003–December 2014. The reference values of TWSA trends are shown as the ensemble means of three different GRACE mascon solutions (i.e., CSR-M, JPL-M, and GSFC-M). The gray stippling indicates regions with non-significant trends (p ≥ 0.05).
Remotesensing 12 03578 g004
Remotesensing 12 03578 g005 550
Figure 5. Time series of TWSA from seven different hydrological models and the corresponding reference values (i.e., the ensemble means of CSR-M, JPL-M, and GSFC-M) in the different regions (CC (a); NEC (b); MDB (c); and NWP (d)) and the whole continent of Australia (e). The gray-shaded area indicates the standard deviation of three different GRACE mascon solutions.
Figure 5. Time series of TWSA from seven different hydrological models and the corresponding reference values (i.e., the ensemble means of CSR-M, JPL-M, and GSFC-M) in the different regions (CC (a); NEC (b); MDB (c); and NWP (d)) and the whole continent of Australia (e). The gray-shaded area indicates the standard deviation of three different GRACE mascon solutions.
Remotesensing 12 03578 g005
Remotesensing 12 03578 g006 550
Figure 6. Spatial distributions of soil moisture storage anomalies (SMSA) trends over Australia from seven different hydrological models (i.e., Noah-3.6 (a); CLSM-F2.5 (b); VIC-4.1.2 (c); WaterGAP-2.2d (d); PCR-GLOBWB-2 (e); CLM-4.5 (f); and AWRA-L v6 (g)) and the corresponding reference values (h) for the period of January 2003–December 2014. The reference values of SMSA trends are shown as the ensemble means of all hydrological models, with the exception of CLSM-F2.5, WaterGAP-2.2d and PCR-GLOBWB-2 models. The gray stippling indicates regions with non-significant trends (p ≥ 0.05).
Figure 6. Spatial distributions of soil moisture storage anomalies (SMSA) trends over Australia from seven different hydrological models (i.e., Noah-3.6 (a); CLSM-F2.5 (b); VIC-4.1.2 (c); WaterGAP-2.2d (d); PCR-GLOBWB-2 (e); CLM-4.5 (f); and AWRA-L v6 (g)) and the corresponding reference values (h) for the period of January 2003–December 2014. The reference values of SMSA trends are shown as the ensemble means of all hydrological models, with the exception of CLSM-F2.5, WaterGAP-2.2d and PCR-GLOBWB-2 models. The gray stippling indicates regions with non-significant trends (p ≥ 0.05).
Remotesensing 12 03578 g006
Remotesensing 12 03578 g007 550
Figure 7. Time series of SMSA from seven different hydrological models and the corresponding reference values (the ensemble means of all hydrological models, with the exception of CLSM-F2.5, WaterGAP-2.2d and PCR-GLOBWB-2 models) in the different regions (CC (a); NEC (b); MDB (c); and NWP (d)) and the whole continent of Australia (e). The gray-shaded area indicates the standard deviation among hydrological models used to calculate the reference values.
Figure 7. Time series of SMSA from seven different hydrological models and the corresponding reference values (the ensemble means of all hydrological models, with the exception of CLSM-F2.5, WaterGAP-2.2d and PCR-GLOBWB-2 models) in the different regions (CC (a); NEC (b); MDB (c); and NWP (d)) and the whole continent of Australia (e). The gray-shaded area indicates the standard deviation among hydrological models used to calculate the reference values.
Remotesensing 12 03578 g007
Remotesensing 12 03578 g008 550
Figure 8. Spatial patterns of groundwater water storage anomalies (GWSA) trends over Australia from five different hydrological models (CLSM-F2.5 (a); WaterGAP-2.2d (b); PCR-GLOBWB-2 (c); CLM-4.5 (d); and AWRA-L v6 (e)) and the corresponding reference values (f) for the period of January 2003–December 2014. The reference values of GWSA trends are separated as the residuals between the reference values of TWSA trends and the reference values of SMSA trends. The gray stippling indicates regions with non-significant trends (p ≥ 0.05).
Figure 8. Spatial patterns of groundwater water storage anomalies (GWSA) trends over Australia from five different hydrological models (CLSM-F2.5 (a); WaterGAP-2.2d (b); PCR-GLOBWB-2 (c); CLM-4.5 (d); and AWRA-L v6 (e)) and the corresponding reference values (f) for the period of January 2003–December 2014. The reference values of GWSA trends are separated as the residuals between the reference values of TWSA trends and the reference values of SMSA trends. The gray stippling indicates regions with non-significant trends (p ≥ 0.05).
Remotesensing 12 03578 g008
Remotesensing 12 03578 g009 550
Figure 9. Time series of GWSA from five different hydrological models and the corresponding reference values in different regions (CC (a); NEC (b); MDB (c); and NWP (d)) and the whole continent of Australia (e). The gray-shaded area indicates the root-sum-of-squares of two uncertainties from the reference values of TWSA and the reference values of SMSA.
Figure 9. Time series of GWSA from five different hydrological models and the corresponding reference values in different regions (CC (a); NEC (b); MDB (c); and NWP (d)) and the whole continent of Australia (e). The gray-shaded area indicates the root-sum-of-squares of two uncertainties from the reference values of TWSA and the reference values of SMSA.
Remotesensing 12 03578 g009
Remotesensing 12 03578 g010 550
Figure 10. Trend differences in different water storage anomalies between hydrological models and reference values.
Figure 10. Trend differences in different water storage anomalies between hydrological models and reference values.
Remotesensing 12 03578 g010
Remotesensing 12 03578 g011 550
Figure 11. Comparison of SMSA trends over Australia (January 2003–December 2014) from three different Global Land Data Assimilation System (GLDAS) models (Noah in GLDAS-2.0 (a); Noah in GLDAS-2.1 (b); CLSM in GLDAS-2.1 (c)). The gray stippling indicates regions without significant trends (p ≥ 0.05).
Figure 11. Comparison of SMSA trends over Australia (January 2003–December 2014) from three different Global Land Data Assimilation System (GLDAS) models (Noah in GLDAS-2.0 (a); Noah in GLDAS-2.1 (b); CLSM in GLDAS-2.1 (c)). The gray stippling indicates regions without significant trends (p ≥ 0.05).
Remotesensing 12 03578 g011
Remotesensing 12 03578 g012 550
Figure 12. Continental-scale mean time series of SMSA over Australia from three different GLDAS models.
Figure 12. Continental-scale mean time series of SMSA over Australia from three different GLDAS models.
Remotesensing 12 03578 g012
Table
Table 1. Summary of primary attributes of different hydrological models used in this study.
Table 1. Summary of primary attributes of different hydrological models used in this study.
DescriptionNoah-3.6CLSM-F2.5VIC-4.1.2WaterGAP-2.2dPCR-GLOBWB-2CLM-4.5AWRA-L v6
Resolution (lat × lon)1° × 1°1° × 1°1° × 1°0.5° × 0.5°0.08° × 0.08°0.94° × 1.25°0.05° × 0.05°
Time span2000–present2000–present2000–present1950–20161958–20151979–20141911–present
SnWSYesYesYesYesYesYesYes
CWSYesYesYesYesYesYesYes
SWSNoNoNoYesYesYesYes
SMSYesYesYesYesYesYesYes
GWSNoYesNoYesYesYesYes
Soil layers41312103
Soil thickness (m)2.01.0VariableVariable1.53.86.0
Climate forcing 1(1)(1)(1)(2)(3)(4)(5)
Human water useNoNoNoYesYesNoNo
CalibrationNoNoNoYesNoNoYes
1 Climate forcing: (1) NOAA/GDAS-GPCP-AGRMET: National Oceanic and Atmospheric Administration/Global Data Assimilation System atmospheric analysis fields, Global Precipitation Climatology Project V1.3, and the Air Force Weather Agency’s AGRicultural METeorological modeling system; (2) WFDEI-GPCC: WATCH Forcing Data methodology applied to ERA-Interim data, Global Precipitation Climatology Centre; (3) CRU-ERA40-ERA-Interim: Climate Research Unit (CRU), European Centre for Medium-Range Weather Forecasts reanalysis production (ERA40, ERA-Interim); (4) GSWP3: The Global Soil Wetness Project phase 3; (5) AWAP: The Australian Water Availability Project. CLSM-F2.5, Catchment Land Surface Model; VIC-4.1.2, Variable Infiltration Capacity macroscale model; WaterGAP-2.2d, Water—Global Assessment and Prognosis; PCR-GLOBWB-2, PCRaster Global Water Balance; CLM-4.5, Community Land Model; AWRA-L v6, Australian Water Resources Assessment Landscape model; SnWS, snow water storage; CWS, canopy water storage; SWS, surface water storage; SMS, soil moisture storage; GWS, groundwater storage.
Table
Table 2. Summary of primary processing details of different Gravity Recovery and Climate Experiment (GRACE) mass concentration block (mascon) solutions used in this study.
Table 2. Summary of primary processing details of different Gravity Recovery and Climate Experiment (GRACE) mass concentration block (mascon) solutions used in this study.
DescriptionCSR-M RL06 v01JPL-M RL06 v01GSFC-M v02.4
Released/native resolution (lat × lon) 10.25° × 0.25°/1° × 1°0.5° × 0.5°/3° × 3°1° × 1°/1° × 1°
Solution spanApril 2002–June 2017April 2002–June 2017Jan 2003–July 2016
Mean removed2004.0–2009.9992004.0–2009.9992004.0–2016.0
Regularization[42][43,44][45]
Background static fieldGGM-05C 2GGM-05CGOCO-05S 3
Tide modelGOT4.8 (d/o 180) 4FES2014b (d/o 180) 5GOT4.7 (d/o 90)
AOD 6ECMWF 7 + MPIOM 8ECMWF + MPIOMECMWF + MOG2D 9
Degree 1 CorrectionsTN-13a 10[47][47]
C20 11 replacementSLR 12 (TN-11)SLR (TN-11)SLR (TN-07)
GIA 13 CorrectionICE6G-D 14ICE6G-DICE6G-D
1 The native resolution of different GRACE mascon solutions is the resolution of different processing centers parameterizing the gravity field and does not represent the native resolution of GRACE (approximately 3°) [1]; 2 GGM, GRACE Gravity Model; 3 GOCO, Gravity Observation Combination; 4 GOT, Goddard/Grenoble Ocean Tide; 5 FES, finite element solution; 6 AOD, Atmosphere and Ocean Dealiasing; 7 ECMWF, European Centre for Medium-Range Weather Forecasts; 8 MPIOM, Max-Planck-Institute for Meteorology Ocean Model; 9 MOG2D, 2DGravity Waves model; 10 TN, technical note; 11 C20, degree 2 order 0 coefficients; 12 SLR, satellite laser ranging; 13 GIA, glacial isostatic adjustment; 14 ICE6G, global ice history model. CSR-M RL06 v01, Center for Space Research release 06 (RL 06) mascon solutions v01; JPL-M RL06 v01, Jet Propulsion Laboratory RL06 mascon solutions v01; GSFC-M v02.4, Goddard Space Flight Center mascon solutions v02.4.
Table
Table 3. Statistical summary of temporal agreement metrics between GRACE mason solutions in Australia. The bold and underlined numbers are the best and the worst values for the metrics, respectively.
Table 3. Statistical summary of temporal agreement metrics between GRACE mason solutions in Australia. The bold and underlined numbers are the best and the worst values for the metrics, respectively.
Mascon SolutionsrRMSE (cm)NSE
CSR–JPL0.980.660.97
CSR–GSFC0.951.270.88
JPL–GSFC0.941.350.86
Table
Table 4. Statistical summary of agreement metrics between hydrological models and the different reference values. The bold and underlined numbers are the best and the worst values for the metrics, respectively.
Table 4. Statistical summary of agreement metrics between hydrological models and the different reference values. The bold and underlined numbers are the best and the worst values for the metrics, respectively.
ModelsTWSASMSAGWSA
rRMSE (cm)NSErRMSE (cm)NSErRMSE (cm)NSE
Noah-3.60.901.650.770.990.480.97---
CLSM-F2.50.871.990.670.952.150.400.312.57−2.01
VIC-4.1.20.871.880.700.980.670.94---
WaterGAP-2.2d0.773.090.200.662.540.170.201.65−0.24
PCR-GLOBWB-20.812.480.480.871.760.600.621.250.28
CLM-4.50.951.050.910.960.790.920.800.900.63
AWRA-L v60.931.440.820.990.470.970.651.300.23
TWSA, total terrestrial water storage anomalies; SMSA, soil moisture storage anomalies; GWSA, groundwater water storage anomalies.
Table
Table 5. Statistical summary of the different water storage trends (mm/year) derived from hydrological models and the reference values over Australia from 2003 to 2014. The statistically non-significant values with Mann–Kendall test (M–K test) at the 95% confidence limit are demonstrated in bold.
Table 5. Statistical summary of the different water storage trends (mm/year) derived from hydrological models and the reference values over Australia from 2003 to 2014. The statistically non-significant values with Mann–Kendall test (M–K test) at the 95% confidence limit are demonstrated in bold.
ModelsTWSASMSAGWSA
TrendsTrendsTrends
Noah-3.61.74 ± 0.461.74 ± 0.46-
CLSM-F2.51.29 ± 0.560.25 ± 0.121.04 ± 0.44
VIC-4.1.21.92 ± 0.391.92 ± 0.39-
WaterGAP-2.2d0.56 ± 0.130.28 ± 0.060.28 ± 0.08
PCR-GLOBWB-20.73 ± 0.31−0.05 ± 0.200.78 ± 0.14
CLM-4.53.79 ± 0.521.26 ± 0.362.53 ± 0.20
AWRA-L v62.02 ± 0.451.42 ± 0.360.58 ± 0.10
Reference 13.15 ± 0.561.58 ± 0.481.57 ± 0.32
1 The reference value of TWSA trend is based on the ensemble average of CSR-M, JPL-M, and GSFC-M-born TWSA trends; the reference value of SMSA trend is based on the average of all hydrological models-derived SWSA trends, except for CLSM-F2.5, WaterGAP-2.2d, and PCR-GLOBWB-2 models; the reference value of GWSA trend is separated as the residual between the reference value of TWSA trend and the reference value of SMSA trend. The uncertainties in trends were mathematically derived from least squares linear regression when decomposing the long-term component [28].
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Yang, X.; Tian, S.; Feng, W.; Ran, J.; You, W.; Jiang, Z.; Gong, X. Spatio-Temporal Evaluation of Water Storage Trends from Hydrological Models over Australia Using GRACE Mascon Solutions. Remote Sens. 2020, 12, 3578. https://doi.org/10.3390/rs12213578

AMA Style

Yang X, Tian S, Feng W, Ran J, You W, Jiang Z, Gong X. Spatio-Temporal Evaluation of Water Storage Trends from Hydrological Models over Australia Using GRACE Mascon Solutions. Remote Sensing. 2020; 12(21):3578. https://doi.org/10.3390/rs12213578

Chicago/Turabian Style

Yang, Xinchun, Siyuan Tian, Wei Feng, Jiangjun Ran, Wei You, Zhongshan Jiang, and Xiaoying Gong. 2020. "Spatio-Temporal Evaluation of Water Storage Trends from Hydrological Models over Australia Using GRACE Mascon Solutions" Remote Sensing 12, no. 21: 3578. https://doi.org/10.3390/rs12213578

APA Style

Yang, X., Tian, S., Feng, W., Ran, J., You, W., Jiang, Z., & Gong, X. (2020). Spatio-Temporal Evaluation of Water Storage Trends from Hydrological Models over Australia Using GRACE Mascon Solutions. Remote Sensing, 12(21), 3578. https://doi.org/10.3390/rs12213578

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop