Ensemble of Machine-Learning Methods for Predicting Gully Erosion Susceptibility
Abstract
:1. Introduction
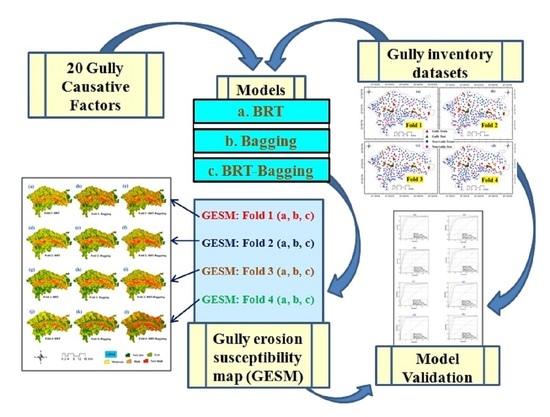
2. Materials and Methods
2.1. Description of the Study Area
2.2. Methodology
2.2.1. Gully Erosion Inventory Map (GEIM)
2.2.2. Dataset Preparation
Topographical Factors
Hydrological Factors
Soil-Related Factors
Lithological Factors
Environmental Factors
2.2.3. Multicollinearity Analysis
2.2.4. Measuring the Variables’ Importance
2.2.5. Machine-Learning Methods
Boosted Regression Tree (BRT)
Bagging
Ensemble of BRT and Bagging
2.2.6. Resampling
K-Fold Cross Validation
2.2.7. Validation and Accuracy Assessment
3. Results
3.1. Multi-Collinearity Analysis
3.2. Determine Best Parameters
3.3. Relative Variables Importance of Gully Erosion Conditioning Factors (GECFs)
3.4. Modeling of Gully Erosion Susceptibility (GES) Mapping
3.5. Validation of GES Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gayen, A.; Pourghasemi, H.R. 30—Spatial modeling of gully erosion: A new ensemble of CART and GLM data-mining algorithms. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Pourghasemi, H.R., Gokceoglu, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 653–669. ISBN 978-0-12-815226-3. [Google Scholar]
- Poesen, J.; Govers, G. Gully erosion in the loam belt of Belgium: Typology and control measures. In Soil Erosion on Agricultural Land Proceedings of A Workshop Sponsored by the British Geomorphological Research Group, Coventry, UK, 1989; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1990; pp. 513–530. [Google Scholar]
- Poesen, J.W. Contribution of gully erosion to sediment production on cultivated lands and rangelands. In Proceedings of an International Symposium, Exeter, UK, 15–19 July 1996 No. 236; IAHS: Wallingford, UK, 1996. [Google Scholar]
- Poesen, J.; Vanwalleghem, T.; Deckers, J. Gullies and closed depressions in the loess belt: Scars of human–environment interactions. In Landscapes and Landforms of Belgium and Luxembourg; World Geomorphological Landscapes; Demoulin, A., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 253–267. ISBN 978-3-319-58239-9. [Google Scholar]
- Poesen, J.; Nachtergaele, J.; Verstraeten, G.; Valentin, C. Gully erosion and environmental change: Importance and research needs. CATENA 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Das, B.; Pal, S.C.; Malik, S. Assessment of flood hazard in a riverine tract between Damodar and Dwarkeswar River, Hugli District, West Bengal, India. Spat. Inf. Res. 2018, 26, 91–101. [Google Scholar] [CrossRef]
- Das, B.; Pal, S.C.; Malik, S.; Chakrabortty, R. Living with floods through geospatial approach: A case study of Arambag C.D. Block of Hugli District, West Bengal, India. SN Appl. Sci. 2019, 1, 329. [Google Scholar] [CrossRef] [Green Version]
- Chowdhuri, I.; Pal, S.C.; Chakrabortty, R. Flood susceptibility mapping by ensemble evidential belief function and binomial logistic regression model on river basin of eastern India. Adv. Space Res. 2020, 65, 1466–1489. [Google Scholar] [CrossRef]
- Malik, S.; Pal, S.C. Application of 2D numerical simulation for rating curve development and inundation area mapping: A case study of monsoon dominated Dwarkeswar river. Int. J. River Basin Manag. 2020, 1–11. [Google Scholar] [CrossRef]
- Pal, S.; Shit, M. Application of RUSLE model for soil loss estimation of Jaipanda watershed, West Bengal. Spat. Inf. Res. 2017. [Google Scholar] [CrossRef]
- Pal, S.C.; Chakrabortty, R. Modeling of water induced surface soil erosion and the potential risk zone prediction in a sub-tropical watershed of Eastern India. Model Earth Syst. Environ. 2019, 5, 369–393. [Google Scholar] [CrossRef]
- Pal, S.C.; Chakrabortty, R. Simulating the impact of climate change on soil erosion in sub-tropical monsoon dominated watershed based on RUSLE, SCS runoff and MIROC5 climatic model. Adv. Space Res. 2019, 64, 352–377. [Google Scholar] [CrossRef]
- Saha, A.; Ghosh, M.; Pal, S.C. Understanding the morphology and development of a rill-gully: An Empirical study of Khoai Badland, West Bengal, India. In Gully Erosion Studies from India and Surrounding Regions; Advances in Science, Technology & Innovation; Shit, P.K., Pourghasemi, H.R., Bhunia, G.S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 147–161. ISBN 978-3-030-23243-6. [Google Scholar]
- Al-Abadi, A.M.; Al-Ali, A.K. Susceptibility mapping of gully erosion using GIS-based statistical bivariate models: A case study from Ali Al-Gharbi District, Maysan Governorate, southern Iraq. Environ. Earth Sci. 2018, 77, 249. [Google Scholar] [CrossRef]
- Chakrabortty, R.; Pal, S.C.; Chowdhuri, I.; Malik, S.; Das, B. Assessing the Importance of static and dynamic causative factors on erosion potentiality using SWAT, EBF with uncertainty and plausibility, logistic regression and novel ensemble model in a sub-tropical environment. J. Indian Soc. Remote Sens. 2020, 48, 765–789. [Google Scholar] [CrossRef]
- Rahmati, O.; Haghizadeh, A.; Pourghasemi, H.R.; Noormohamadi, F. Gully erosion susceptibility mapping: The role of GIS-based bivariate statistical models and their comparison. Nat. Hazards 2016, 82, 1231–1258. [Google Scholar] [CrossRef]
- Amiri, M.; Pourghasemi, H.R.; Ghanbarian, G.A.; Afzali, S.F. Assessment of the importance of gully erosion effective factors using Boruta algorithm and its spatial modeling and mapping using three machine learning algorithms. Geoderma 2019, 340, 55–69. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Yousefi, S.; Kornejady, A.; Cerdà, A. Performance assessment of individual and ensemble data-mining techniques for gully erosion modeling. Sci. Total Environ. 2017, 609, 764–775. [Google Scholar] [CrossRef] [Green Version]
- Gayen, A.; Pourghasemi, H.R.; Saha, S.; Keesstra, S.; Bai, S. Gully erosion susceptibility assessment and management of hazard-prone areas in India using different machine learning algorithms. Sci. Total Environ. 2019, 668, 124–138. [Google Scholar] [CrossRef]
- Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluating the influence of geo-environmental factors on gully erosion in a semi-arid region of Iran: An integrated framework. Sci. Total Environ. 2017, 579, 913–927. [Google Scholar] [CrossRef]
- Azareh, A.; Rahmati, O.; Rafiei-Sardooi, E.; Sankey, J.B.; Lee, S.; Shahabi, H.; Ahmad, B.B. Modelling gully-erosion susceptibility in a semi-arid region, Iran: Investigation of applicability of certainty factor and maximum entropy models. Sci. Total Environ. 2019, 655, 684–696. [Google Scholar] [CrossRef]
- Arabameri, A.; Asadi Nalivan, O.; Chandra Pal, S.; Chakrabortty, R.; Saha, A.; Lee, S.; Pradhan, B.; Tien Bui, D. Novel machine learning approaches for modelling the gully erosion susceptibility. Remote Sens. 2020, 12, 2833. [Google Scholar] [CrossRef]
- Band, S.S.; Janizadeh, S.; Chandra Pal, S.; Saha, A.; Chakrabortty, R.; Shokri, M.; Mosavi, A. Novel ensemble approach of Deep Learning Neural Network (DLNN) model and Particle Swarm Optimization (PSO) algorithm for prediction of gully erosion susceptibility. Sensors 2020, 20, 5609. [Google Scholar] [CrossRef]
- Puente, C.; Olague, G.; Smith, S.V.; Bullock, S.H.; Hinojosa-Corona, A.; González-Botello, M.A. A Genetic programming approach to estimate vegetation cover in the context of soil erosion assessment. Photogramm. Eng. Remote Sens. 2011, 77, 363–376. [Google Scholar] [CrossRef] [Green Version]
- Puente, C.; Olague, G.; Trabucchi, M.; Arjona-Villicaña, P.D.; Soubervielle-Montalvo, C. Synthesis of vegetation indices using genetic programming for soil erosion estimation. Remote Sens. 2019, 11, 156. [Google Scholar] [CrossRef] [Green Version]
- Cabral, A.I.R.; Silva, S.; Silva, P.C.; Vanneschi, L.; Vasconcelos, M.J. Burned area estimations derived from Landsat ETM+ and OLI data: Comparing genetic/ programming with maximum likelihood and classification and regression trees. ISPRS J. Photogramm. Remote Sens. 2018, 142, 94–105. [Google Scholar] [CrossRef]
- Kariminejad, N.; Hosseinalizadeh, M.; Pourghasemi, H.R.; Bernatek-Jakiel, A.; Alinejad, M. GIS-based susceptibility assessment of the occurrence of gully headcuts and pipe collapses in a semi-arid environment: Golestan Province, NE Iran. Land Degrad. Dev. 2019, 30, 2211–2225. [Google Scholar] [CrossRef]
- Roy, P.; Chakrabortty, R.; Chowdhuri, I.; Malik, S.; Das, B.; Pal, S.C. Development of different machine learning ensemble classifier for gully erosion susceptibility in gandheswari watershed of West Bengal, India. In Machine Learning for Intelligent Decision Science; Algorithms for Intelligent Systems; Rout, J.K., Rout, M., Das, H., Eds.; Springer: Singapore, 2020; pp. 1–26. ISBN 9789811536892. [Google Scholar]
- Zhang, W.; Du, Z.; Zhang, D.; Yu, S.; Hao, Y. Boosted regression tree model-based assessment of the impacts of meteorological drivers of hand, foot and mouth disease in Guangdong, China. Sci. Total Environ. 2016, 553, 366–371. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Lombardo, L. Comparative assessment using boosted regression trees, binary logistic regression, frequency ratio and numerical risk factor for gully erosion susceptibility modelling. CATENA 2019, 183, 104223. [Google Scholar] [CrossRef]
- Arabameri, A.; Yamani, M.; Pradhan, B.; Melesse, A.; Shirani, K.; Tien Bui, D. Novel ensembles of COPRAS multi-criteria decision-making with logistic regression, boosted regression tree, and random forest for spatial prediction of gully erosion susceptibility. Sci. Total Environ. 2019, 688, 903–916. [Google Scholar] [CrossRef]
- Zabihi, M.; Pourghasemi, H.R.; Motevalli, A.; Zakeri, M.A. Gully erosion modeling using GIS-based data mining techniques in Northern Iran: A comparison between boosted regression tree and multivariate adaptive regression spline. In Natural Hazards GIS-Based Spatial Modeling Using Data Mining Techniques; Advances in Natural and Technological Hazards Research; Pourghasemi, H.R., Rossi, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 1–26. ISBN 978-3-319-73383-8. [Google Scholar]
- Nhu, V.-H.; Janizadeh, S.; Avand, M.; Chen, W.; Farzin, M.; Omidvar, E.; Shirzadi, A.; Shahabi, H.; Clague, J.J.; Jaafari, A.; et al. GIS-based gully erosion susceptibility mapping: A comparison of computational ensemble data mining models. Appl. Sci. 2020, 10, 2039. [Google Scholar] [CrossRef] [Green Version]
- Shit, P.K.; Paira, R.; Bhunia, G.; Maiti, R. Modeling of potential gully erosion hazard using geo-spatial technology at Garbheta block, West Bengal in India. Model Earth Syst. Environ. 2015, 1, 2. [Google Scholar] [CrossRef]
- Shit, P.K.; Maiti, R.K. Mechanism of gully-head retreat—A study at Ganganir Danga, Paschim Medinipur, West Bengal. Ethiop. J. Environ. Stud. Manag. 2012, 5, 332–342. [Google Scholar] [CrossRef] [Green Version]
- Chernick, M.R. Resampling methods. WIREs Data Min. Knowl. Discov. 2012, 2, 255–262. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Pourghasemi, H.R.; Rezaei, K.; Kerle, N. Spatial modelling of gully erosion using GIS and R programing: A comparison among three data mining algorithms. Appl. Sci. 2018, 8, 1369. [Google Scholar] [CrossRef] [Green Version]
- Conforti, M.; Aucelli, P.P.C.; Robustelli, G.; Scarciglia, F. Geomorphology and GIS analysis for mapping gully erosion susceptibility in the Turbolo stream catchment (Northern Calabria, Italy). Nat. Hazards 2011, 56, 881–898. [Google Scholar] [CrossRef]
- Barnes, N.; Luffman, I.; Nandi, A. Gully erosion and freeze-thaw processes in clay-rich soils, Northeast Tennessee, USA. GeoResJ 2016, 9–12, 67–76. [Google Scholar] [CrossRef]
- Ollobarren, P.; Capra, A.; Gelsomino, A.; La Spada, C. Effects of ephemeral gully erosion on soil degradation in a cultivated area in Sicily (Italy). CATENA 2016, 145, 334–345. [Google Scholar] [CrossRef]
- Arabameri, A.; Chen, W.; Loche, M.; Zhao, X.; Li, Y.; Lombardo, L.; Cerda, A.; Pradhan, B.; Bui, D.T. Comparison of machine learning models for gully erosion susceptibility mapping. Geosci. Front. 2020, 11, 1609–1620. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.T.; Zhang, T.; Zhang, L.; Chai, H.; et al. Landslide susceptibility modeling based on GIS and novel bagging-based kernel logistic regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.; Xiaoling, G.; Hua, Y. Variable selection using mean decrease accuracy and mean decrease gini based on random forest. In Proceedings of the 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 26–28 August 2016; pp. 219–224. [Google Scholar]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J. Boosted Regression Trees for Ecological Modeling. Online Tutorial. 3 July 2011, p. 22. Available online: http://cran.r-project.org/web/packages/dismo/vignettes/brt.pdf (accessed on 1 November 2020).
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.-X.; Chen, W.; Ahmad, B.B. Landslide susceptibility mapping using J48 Decision Tree with AdaBoost, Bagging and Rotation Forest ensembles in the Guangchang area (China). CATENA 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Chakrabortty, R.; Pal, S.C.; Sahana, M.; Mondal, A.; Dou, J.; Pham, B.T.; Yunus, A.P. Soil erosion potential hotspot zone identification using machine learning and statistical approaches in eastern India. Nat. Hazards 2020. [Google Scholar] [CrossRef]
- Hair, J.F. Multivariate Data Analysis; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2006; ISBN 978-0-13-032929-5. [Google Scholar]
- Bernatek-Jakiel, A.; Poesen, J. Subsurface erosion by soil piping: Significance and research needs. Earth Sci. Rev. 2018, 185, 1107–1128. [Google Scholar] [CrossRef]










| Factors | Collinearity Statistics | |||||||
|---|---|---|---|---|---|---|---|---|
| Fold 1 | Fold 2 | Fold 3 | Fold 4 | |||||
| TOL | VIF | TOL | VIF | TOL | VIF | TOL | VIF | |
| SPI | 0.231 | 4.330 | 0.233 | 4.288 | 0.236 | 4.237 | 0.251 | 3.981 |
| Soil texture | 0.225 | 4.450 | 0.268 | 3.736 | 0.255 | 3.924 | 0.854 | 1.171 |
| Iron oxide | 0.255 | 3.920 | 0.842 | 1.188 | 0.337 | 2.969 | 0.604 | 1.655 |
| Lineament density | 0.845 | 1.183 | 0.592 | 1.690 | 0.731 | 1.368 | 0.262 | 3.813 |
| Geomorphology | 0.716 | 1.397 | 0.749 | 1.335 | 0.458 | 2.183 | 0.728 | 1.374 |
| Slope | 0.321 | 3.113 | 0.339 | 2.953 | 0.819 | 1.221 | 0.380 | 2.630 |
| Geology | 0.244 | 4.104 | 0.950 | 1.053 | 0.251 | 3.982 | 0.310 | 3.228 |
| Rainfall | 0.278 | 3.599 | 0.779 | 1.283 | 0.271 | 3.692 | 0.328 | 3.051 |
| Ferrous minerals | 0.291 | 3.434 | 0.258 | 3.870 | 0.343 | 2.911 | 0.467 | 2.143 |
| Profile curvature | 0.602 | 1.662 | 0.515 | 1.942 | 0.575 | 1.738 | 0.695 | 1.439 |
| Elevation | 0.661 | 1.513 | 0.642 | 1.559 | 0.613 | 1.631 | 0.653 | 1.531 |
| Plan curvature | 0.428 | 2.339 | 0.374 | 2.675 | 0.412 | 2.425 | 0.482 | 2.074 |
| Drainage density | 0.412 | 2.425 | 0.421 | 2.376 | 0.376 | 2.658 | 0.378 | 2.644 |
| NDVI | 0.739 | 1.353 | 0.784 | 1.275 | 0.721 | 1.387 | 0.741 | 1.350 |
| Distance to drainage | 0.521 | 1.921 | 0.512 | 1.955 | 0.491 | 2.038 | 0.505 | 1.981 |
| LULC | 0.760 | 1.316 | 0.820 | 1.219 | 0.819 | 1.220 | 0.784 | 1.275 |
| TWI | 0.375 | 2.666 | 0.383 | 2.614 | 0.327 | 3.056 | 0.358 | 2.790 |
| Aspect | 0.477 | 2.097 | 0.776 | 1.288 | 0.321 | 3.113 | 0.225 | 4.447 |
| Lithology | 0.504 | 1.985 | 0.682 | 1.466 | 0.283 | 3.536 | 0.332 | 3.013 |
| TRI | 0.263 | 3.806 | 0.762 | 1.312 | 0.214 | 4.671 | 0.261 | 3.833 |
| Resampling | Number of Trees | Interaction Depth | Shrinkage | Number of Minobsin Node |
|---|---|---|---|---|
| 1 fold CV | 50 | 2 | 0.1 | 10 |
| 2 fold CV | 50 | 2 | 0.1 | 10 |
| 3 fold CV | 50 | 2 | 0.1 | 10 |
| 4 fold CV | 150 | 3 | 0.1 | 10 |
| Resampling | Sigma | Cost |
|---|---|---|
| 1 fold CV | 0.0507 | 0.5 |
| 2 fold CV | 0.0478 | 0.5 |
| 3 fold CV | 0.0671 | 0.25 |
| 4 fold CV | 0.0483 | 64 |
| Resampling | Number of Tree | m Try |
|---|---|---|
| 1 fold CV | 200 | 8 |
| 2 fold CV | 200 | 7 |
| 3 fold CV | 200 | 8 |
| 4 fold CV | 200 | 17 |
| Factors | Relative Importance Value | |||
|---|---|---|---|---|
| Fold 1 | Fold 2 | Fold 3 | Fold 4 | |
| SPI | 2.74 | 2.91 | 2.21 | 2.54 |
| Soil Texture | 23.47 | 24.51 | 25.34 | 24.84 |
| Iron Oxide | 0.75 | 0.78 | 0.81 | 0.64 |
| Lineament Density | 6.41 | 7.21 | 6.84 | 7.91 |
| Geomorphology | 48.75 | 47.21 | 50.28 | 52.48 |
| Slope | 72.41 | 76.85 | 74.61 | 75.51 |
| Geology | 15.24 | 16.28 | 17.21 | 16.24 |
| Rainfall | 10.28 | 12.54 | 13.08 | 11.45 |
| Ferrous Minerals | 27.54 | 24.58 | 27.14 | 25.41 |
| Profile Curvature | 54.27 | 55.44 | 52.47 | 53.47 |
| Elevation | 42.84 | 44.74 | 41.75 | 40.81 |
| Plan Curvature | 5.85 | 6.41 | 5.78 | 5.5 |
| Drainage Density | 65.74 | 65.86 | 64.79 | 66.71 |
| NDVI | 9.82 | 8.75 | 9.14 | 8.92 |
| Distance To Drainage | 4.65 | 5.52 | 4.21 | 5.71 |
| LULC | 68.41 | 65.82 | 66.78 | 70.21 |
| TWI | 30.28 | 32.28 | 31.42 | 34.72 |
| Aspect | 28.51 | 27.63 | 29.45 | 26.58 |
| Lithology | 27.68 | 27.45 | 26.94 | 27.12 |
| TRI | 14.56 | 14.92 | 15.71 | 15.52 |
| Susceptibility Class | BRT | Bagging | BRT-Bagging |
|---|---|---|---|
| Fold 1 | (Value in %) | ||
| Very Low | 14.55 | 22.94 | 17.62 |
| Low | 29.46 | 19.77 | 26.43 |
| Moderate | 26.56 | 17.60 | 19.52 |
| High | 20.11 | 22.72 | 14.69 |
| Very High | 9.32 | 16.98 | 21.73 |
| Fold 2 | (Value in %) | ||
| Very Low | 18.61 | 24.34 | 14.40 |
| Low | 27.21 | 24.06 | 26.72 |
| Moderate | 29.31 | 22.00 | 20.81 |
| High | 15.39 | 17.76 | 19.24 |
| Very High | 9.48 | 11.84 | 18.82 |
| Fold 3 | (Value in %) | ||
| Very Low | 23.55 | 24.57 | 16.37 |
| Low | 29.02 | 22.57 | 24.72 |
| Moderate | 24.03 | 21.30 | 20.25 |
| High | 12.28 | 20.87 | 19.54 |
| Very High | 11.10 | 10.68 | 19.12 |
| Fold 4 | (Value in %) | ||
| Very Low | 18.50 | 27.03 | 26.20 |
| Low | 29.47 | 23.48 | 15.11 |
| Moderate | 26.69 | 19.33 | 13.83 |
| High | 16.16 | 17.15 | 15.46 |
| Very High | 9.18 | 13.01 | 29.41 |
| Models | Resampling | Stage | Evaluate Parameters | ||||
|---|---|---|---|---|---|---|---|
| Sensitivity | Specificity | NPV | PPV | AUC | |||
| BRT | Fold 1 | Train | 0.84 | 0.87 | 0.84 | 0.86 | 0.874 |
| Test | 0.79 | 0.83 | 0.77 | 0.84 | 0.843 | ||
| Fold 2 | Train | 0.89 | 0.9 | 0.92 | 0.93 | 0.894 | |
| Test | 0.83 | 0.75 | 0.74 | 0.77 | 0.854 | ||
| Fold 3 | Train | 0.86 | 0.82 | 0.81 | 0.89 | 0.902 | |
| Test | 0.81 | 0.75 | 0.71 | 0.75 | 0.863 | ||
| Fold 4 | Train | 0.85 | 0.87 | 0.88 | 0.83 | 0.915 | |
| Test | 0.83 | 0.84 | 0.77 | 0.8 | 0.876 | ||
| Bagging | Fold 1 | Train | 0.89 | 0.92 | 0.9 | 0.89 | 0.937 |
| Test | 0.74 | 0.74 | 0.71 | 0.81 | 0.851 | ||
| Fold 2 | Train | 0.85 | 0.91 | 0.89 | 0.87 | 0.953 | |
| Test | 0.82 | 0.69 | 0.71 | 0.76 | 0.861 | ||
| Fold 3 | Train | 0.92 | 0.89 | 0.91 | 0.88 | 0.916 | |
| Test | 0.72 | 0.82 | 0.67 | 0.84 | 0.856 | ||
| Fold 4 | Train | 0.86 | 0.89 | 0.82 | 0.91 | 0.922 | |
| Test | 0.79 | 0.85 | 0.75 | 0.71 | 0.884 | ||
| BRT-Bagging | Fold 1 | Train | 0.94 | 0.92 | 0.96 | 0.93 | 0.967 |
| Test | 0.91 | 0.89 | 0.91 | 0.89 | 0.923 | ||
| Fold 2 | Train | 0.91 | 0.94 | 0.91 | 0.95 | 0.954 | |
| Test | 0.83 | 0.85 | 0.89 | 0.91 | 0.935 | ||
| Fold 3 | Train | 0.94 | 0.93 | 0.96 | 0.93 | 0.972 | |
| Test | 0.76 | 0.86 | 0.86 | 0.9 | 0.938 | ||
| Fold 4 | Train | 0.94 | 0.96 | 0.91 | 0.92 | 0.981 | |
| Test | 0.83 | 0.87 | 0.8 | 0.9 | 0.942 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, S.C.; Arabameri, A.; Blaschke, T.; Chowdhuri, I.; Saha, A.; Chakrabortty, R.; Lee, S.; Band, S.S. Ensemble of Machine-Learning Methods for Predicting Gully Erosion Susceptibility. Remote Sens. 2020, 12, 3675. https://doi.org/10.3390/rs12223675
Pal SC, Arabameri A, Blaschke T, Chowdhuri I, Saha A, Chakrabortty R, Lee S, Band SS. Ensemble of Machine-Learning Methods for Predicting Gully Erosion Susceptibility. Remote Sensing. 2020; 12(22):3675. https://doi.org/10.3390/rs12223675
Chicago/Turabian StylePal, Subodh Chandra, Alireza Arabameri, Thomas Blaschke, Indrajit Chowdhuri, Asish Saha, Rabin Chakrabortty, Saro Lee, and Shahab. S. Band. 2020. "Ensemble of Machine-Learning Methods for Predicting Gully Erosion Susceptibility" Remote Sensing 12, no. 22: 3675. https://doi.org/10.3390/rs12223675
APA StylePal, S. C., Arabameri, A., Blaschke, T., Chowdhuri, I., Saha, A., Chakrabortty, R., Lee, S., & Band, S. S. (2020). Ensemble of Machine-Learning Methods for Predicting Gully Erosion Susceptibility. Remote Sensing, 12(22), 3675. https://doi.org/10.3390/rs12223675