Figure 1.
Overview map of the study area Hunsrück-Hochwald National Park.
Figure 1.
Overview map of the study area Hunsrück-Hochwald National Park.
Figure 2.
Tree species distribution within the study area Hunsrück-Hochwald National Park (
left) and digital elevation model derived from ALS point clouds (
right). The ALS point clouds have been provided by
LVermGeo, while the tree species classification is the result of Stoffels et al. [
31]. Coordinates are shown in ETRS89/UTM system (EPSG 25832).
Figure 2.
Tree species distribution within the study area Hunsrück-Hochwald National Park (
left) and digital elevation model derived from ALS point clouds (
right). The ALS point clouds have been provided by
LVermGeo, while the tree species classification is the result of Stoffels et al. [
31]. Coordinates are shown in ETRS89/UTM system (EPSG 25832).
Figure 3.
ALS flight lines and study area Hunsrück-Hochwald National Park. Coordinates are shown in ETRS89/UTM system (EPSG 25832).
Figure 3.
ALS flight lines and study area Hunsrück-Hochwald National Park. Coordinates are shown in ETRS89/UTM system (EPSG 25832).
Figure 4.
Fifteen year average (1989–2012) of the wind direction and wind speed in the study area (
left) and wind rose diagram of the same area and time window (
right). Both figures have been derived from daily wind models provided by Krähenmann et al. [
34]. Coordinates are shown in ETRS89/UTM system (EPSG 25832).
Figure 4.
Fifteen year average (1989–2012) of the wind direction and wind speed in the study area (
left) and wind rose diagram of the same area and time window (
right). Both figures have been derived from daily wind models provided by Krähenmann et al. [
34]. Coordinates are shown in ETRS89/UTM system (EPSG 25832).
Figure 5.
Dominating soil substrates (left) and soil moisture regimes (right) in the study area. Coordinates are shown in ETRS89/UTM system (EPSG 25832).
Figure 5.
Dominating soil substrates (left) and soil moisture regimes (right) in the study area. Coordinates are shown in ETRS89/UTM system (EPSG 25832).
Figure 6.
A duplicate point filter with filtering radius R is applied to points associated with vegetation (left). The resulting filtered point cloud serves as the input for a density filter (center). Points with more than 3 neighboring points within radius R are omitted. Working principle of the vertical line filter with maximum horizontal distance R and z-axis scaled by factor 4 (right).
Figure 6.
A duplicate point filter with filtering radius R is applied to points associated with vegetation (left). The resulting filtered point cloud serves as the input for a density filter (center). Points with more than 3 neighboring points within radius R are omitted. Working principle of the vertical line filter with maximum horizontal distance R and z-axis scaled by factor 4 (right).
Figure 7.
The filtered point cloud serves as the input for the clustering algorithm (left). A point is assigned to the most frequent class of its neighboring points within radius 1.5R. To prefer linear structures, the z-axis is scaled by factor . A regression vector is fitted to each trunk cluster (center). Implausible vectors are omitted from further analyses. Each regression vector defines a local coordinate system, with axes v, z and a (right). The black dots represent the trunk points, while the red dot corresponds to the trunk root.
Figure 7.
The filtered point cloud serves as the input for the clustering algorithm (left). A point is assigned to the most frequent class of its neighboring points within radius 1.5R. To prefer linear structures, the z-axis is scaled by factor . A regression vector is fitted to each trunk cluster (center). Implausible vectors are omitted from further analyses. Each regression vector defines a local coordinate system, with axes v, z and a (right). The black dots represent the trunk points, while the red dot corresponds to the trunk root.
Figure 8.
Relative direct solar radiation depending on site aspect for differing site slopes at solar noon in summer at a geographic latitude of 50°N.
Figure 8.
Relative direct solar radiation depending on site aspect for differing site slopes at solar noon in summer at a geographic latitude of 50°N.
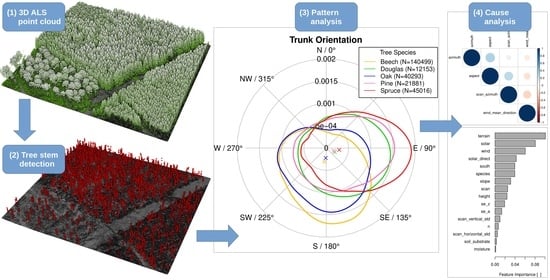
Figure 9.
Density plots of the trunk inclination (left) and trunk orientation (right) grouped by differing significance levels of the trunk inclination. For each group, the mean trunk orientation is marked with a cross.
Figure 9.
Density plots of the trunk inclination (left) and trunk orientation (right) grouped by differing significance levels of the trunk inclination. For each group, the mean trunk orientation is marked with a cross.
Figure 10.
Site aspect in relation to slope (left), scan compass direction in relation to the scan zenith angle (center) and trunk orientation in relation to the trunk inclination (right).
Figure 10.
Site aspect in relation to slope (left), scan compass direction in relation to the scan zenith angle (center) and trunk orientation in relation to the trunk inclination (right).
Figure 11.
Density of the tree trunks for the explanatory variables wind direction (left), site aspect (center) and scan direction (right) grouped by tree species.
Figure 11.
Density of the tree trunks for the explanatory variables wind direction (left), site aspect (center) and scan direction (right) grouped by tree species.
Figure 12.
Pearson’s product moment correlation coefficients for scalar variables (left) and directed variables (right).
Figure 12.
Pearson’s product moment correlation coefficients for scalar variables (left) and directed variables (right).
Figure 13.
Influence of the tree species on the trunk inclination (left) and trunk orientation (right). The deciduous trees tend to lean to the South, while the conifers tend to lean to the East. The orientation follows the site aspect, while a general trend to the South can be observed.
Figure 13.
Influence of the tree species on the trunk inclination (left) and trunk orientation (right). The deciduous trees tend to lean to the South, while the conifers tend to lean to the East. The orientation follows the site aspect, while a general trend to the South can be observed.
Figure 14.
Influence of the slope on the tree inclination (left) and effect of the aspect on the trunk orientation (right).
Figure 14.
Influence of the slope on the tree inclination (left) and effect of the aspect on the trunk orientation (right).
Figure 15.
Effect of the site aspect on differing tree species.
Figure 15.
Effect of the site aspect on differing tree species.
Figure 16.
Permutation feature importance of the Random Forest regressor (left) and regression coefficients of selected linear trunk inclination models (right). The coefficients are scaled by to display them in the same plot. The given 98% and 80% confidence intervals are based on bootstrapping.
Figure 16.
Permutation feature importance of the Random Forest regressor (left) and regression coefficients of selected linear trunk inclination models (right). The coefficients are scaled by to display them in the same plot. The given 98% and 80% confidence intervals are based on bootstrapping.
Figure 17.
Permutation feature importance of the Random Forest regressor (left) and regression coefficients of selected linear trunk orientation models (right). The coefficients are scaled by to display them in the same plot. The given 98% and 80% confidence intervals are based on bootstrapping.
Figure 17.
Permutation feature importance of the Random Forest regressor (left) and regression coefficients of selected linear trunk orientation models (right). The coefficients are scaled by to display them in the same plot. The given 98% and 80% confidence intervals are based on bootstrapping.
Figure 18.
Residuals of the linear trunk orientation model Azimuth 6 depending on observed trunk orientation (top-left), tree species (top-right), site aspect (bottom-left) and scan direction (bottom-right).
Figure 18.
Residuals of the linear trunk orientation model Azimuth 6 depending on observed trunk orientation (top-left), tree species (top-right), site aspect (bottom-left) and scan direction (bottom-right).
Table 1.
Comparison of surface area with the amount of detected stems.
Table 1.
Comparison of surface area with the amount of detected stems.
| | Beech | Douglas | Oak | Pine | Spruce |
|---|
| Area of classification layer | 36.8% | 11.4% | 13.9% | 9.8% | 28.1% |
| Number of detected stems | 40.7% | 6.5% | 11.5% | 8.3% | 32.9% |
Table 2.
Distribution of soil properties by tree species.
Table 2.
Distribution of soil properties by tree species.
| | | Tree Species |
|---|
| Soil Property | Beech | Douglas | Oak | Pine | Spruce |
|---|
| Soil substrate | Quarzite | 73.5% | 72.2% | 70.7% | 68.8% | 67.4% |
| Quarzite & Shales | 26.2% | 27.5% | 27.8% | 30.5% | 32.4% |
| Shales | 0.3% | 0.3% | 1.5% | 0.6% | 0.2% |
| Soil moisture | dry | 3.1% | 5.4% | 10.0% | 5.6% | 3.7% |
| moist | 82.2% | 84.3% | 85.8% | 83.4% | 81.8% |
| very moist | 14.7% | 10.3% | 4.2% | 11.0% | 14.4% |
Table 3.
Inclination and orientation of the significantly inclined trunks for different species.
Table 3.
Inclination and orientation of the significantly inclined trunks for different species.
| | Beech | Douglas | Oak | Pine | Spruce | Average |
|---|
| ± | ± | ± | ± | ± | ± |
| ± | ± | ± | ± | ± | ± |
Table 4.
Amount of trees inclined with a specific explanatory variable for different groups.
Table 4.
Amount of trees inclined with a specific explanatory variable for different groups.
| | | Inclination Direction |
|---|
| Group | Southward | Down-Slope | Leeward | in Scan Direction |
|---|
| Species | Beech | 70.8% | 77.2% | 39.9% | 40.3% |
| Douglas | 56.2% | 60.5% | 61.0% | 50.4% |
| Oak | 65.5% | 74.1% | 44.5% | 42.9% |
| Pine | 54.5% | 63.4% | 58.8% | 43.1% |
| Spruce | 53.6% | 51.8% | 67.5% | 53.7% |
| Species Type | Conifer | 54.3% | 56.3% | 64.1% | 50.2% |
| Deciduous | 69.6% | 76.5% | 40.9% | 40.9% |
| Root System | Flat | 53.6% | 51.8% | 67.5% | 53.7% |
| Heart | 69.7% | 75.9% | 41.6% | 41.1% |
| Tap | 61.6% | 70.3% | 49.6% | 43.0% |
| | Total | 66.0% | 71.3% | 46.8% | 43.3% |
Table 5.
Total and partial per regression coefficient of the linear trunk inclination models. Coefficients significantly different from zero are marked in bold. Significant inter group differences are marked in italics.
Table 5.
Total and partial per regression coefficient of the linear trunk inclination models. Coefficients significantly different from zero are marked in bold. Significant inter group differences are marked in italics.
| | Zenith 1 | Zenith 2 | Zenith 3 | Zenith 4 | Zenith 5 | Zenith 6 |
|---|
| (Intercept) | 0.010 | 0.000 | 0.000 | | | 0.096 |
| se_z | 0.308 | 0.314 | 0.312 | 0.312 | 0.311 | 0.307 |
| se_a | 0.020 | 0.021 | 0.025 | 0.025 | 0.025 | 0.024 |
| n | 0.002 | 0.003 | | | | |
| scan_horizontal_std | 0.009 | 0.010 | 0.011 | 0.011 | 0.011 | 0.010 |
| scan_vertical_std | 0.000 | 0.000 | | | | |
| scan_zenith | 0.001 | 0.001 | | | | |
| wind_mean_speed | 0.000 | 0.000 | | | | |
| solar_direct | 0.001 | 0.001 | | | | |
| height | 0.076 | 0.067 | 0.074 | 0.074 | 0.075 | 0.083 |
| slope | 0.018 | 0.013 | 0.013 | 0.013 | 0.013 | 0.018 |
| species:moisture:soil_substrate | | 0.004 | 0.004 | | | |
| species | | | | 0.001 | 0.098 | |
| moisture | | | | 0.000 | | |
| soil_substrate | | | | 0.001 | | |
| Total | 0.573 | 0.590 | 0.586 | 0.581 | 0.578 | 0.570 |
Table 6.
Average explained variance per regression coefficient for the linear trunk orientation models. Coefficients significantly different from zero are marked in bold. Significant inter group differences are marked in italics. Measures are based on the training data set .
Table 6.
Average explained variance per regression coefficient for the linear trunk orientation models. Coefficients significantly different from zero are marked in bold. Significant inter group differences are marked in italics. Measures are based on the training data set .
| | Azimuth 1 | Azimuth 2 | Azimuth 3 | Azimuth 4 | Azimuth 5 | Azimuth 6 |
|---|
| terrain | 8.9% | | | | | |
| terrain:species | | 8.5% | 8.3% | 8.4% | 8.5% | 8.5% |
| solar | 4.1%
| | | | | |
| solar:species | | 6.2% | 6.3% | 6.3% | 6.1% | |
| solar:species_type | | | | | | 6.2% |
| wind | −0.1% | | | | | |
| wind:species | | 2.9% | 3.2% | 3.2% | | |
| wind:species:height | | | | | 3.6% | 3.6% |
| south | 0.3% | | −0.1% | | | |
| south:species | | 0.5% | | | | |
| scan | 0.9%
| 0.8%
| 0.8%
| 0.8%
| 0.8%
| 0.8%
|
| Total | 14.0%
| 18.8%
| 18.5%
| 18.6%
| 19.1%
| 19.1%
|
Table 7.
Accuracy metrics of the trunk orientation prediction (coefficient of determination , mean angular deviation , circular standard deviation and the amount of trunks inclined with the model ). The metrics are based on the training data set .
Table 7.
Accuracy metrics of the trunk orientation prediction (coefficient of determination , mean angular deviation , circular standard deviation and the amount of trunks inclined with the model ). The metrics are based on the training data set .
| | RF | Azimuth 1 | Azimuth 2 | Azimuth 3 | Azimuth 4 | Azimuth 5 | Azimuth 6 |
|---|
| | | | | | | |
| | | | | | | |
| | | | | | | |
| 82.8% | 71.9% | 74.7% | 75.0% | 75.0% | 75.3% | 75.3% |
Table 8.
Average explained variance per regression coefficient of the regression model Azimuth 6 depending on tree species. The measures are based on the validation data set . If applicable, coefficients significantly different from zero are highlighted in bold.
Table 8.
Average explained variance per regression coefficient of the regression model Azimuth 6 depending on tree species. The measures are based on the validation data set . If applicable, coefficients significantly different from zero are highlighted in bold.
| | Beech | Douglas | Oak | Pine | Spruce | Conifer | Deciduous | Total |
|---|
| terrain:species | 11.4%
| 3.2% | 9.8%
| 5.7%
| 0.3% | 2.2% | 11.1% | 8.4% |
| solar:species_type | 9.0% | 0.2% | 8.0% | 0.3% | 0.0% | 0.1% | 8.8%
| 6.1% |
| wind:species:height | 2.0%
| 5.7%
| 0.6% | 4.1%
| 11.1%
| 8.3% | 1.7% | 3.7% |
| scan | 1.2% | 0.0% | 0.8% | 0.8% | −0.4% | −0.0% | 1.1% | 0.8%
|
| Total | 23.7% | 9.1% | 19.2% | 10.9% | 11.0% | 10.7% | 22.7% | 19.0% |