A Parallax Shift Effect Correction Based on Cloud Height for Geostationary Satellites and Radar Observations
Abstract
:1. Introduction
2. Nature of Parallax Shift Problem and Vicente et al./Koenig Method
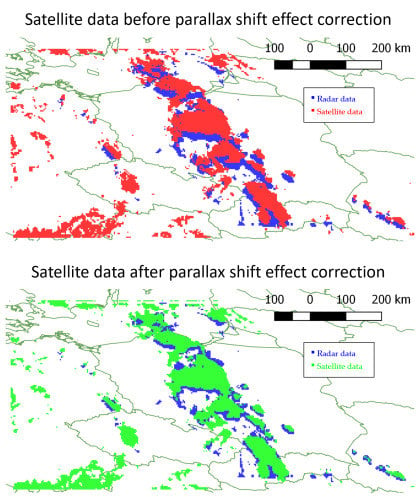
2.1. Problem Description
2.2. Vicente et al./Koenig Method
- Designate satellite position in the Cartesian coordinates system;
- Designate the position of cloud top image in the Cartesian coordinates system using Equation (5);
- Designate vector ;
- Designate coefficient , which allows Cartesian coordinates of the cloud top to be calculated using the following equations (see Figure 5):where is described by the ellipsoid parametric equation:where and are the parametric latitude and longitude (see Figure 2). Therefore, Equation (9) can be presented as a set of equations:Squaring each equation and adding them according to their sides leads to a square equation, which can be solved with respect to c:
- Apply c to calculate the Cartesian coordinates of - , , and .
- Calculate the geocentric ellipsoidal coordinates of :
- If required for further computation, a geodetic latitude can be calculated:
3. Parallax Error Correction Methods with Lower Error
3.1. Vicente et al./Koenig Augmentation
3.2. Ellipsoid Model with Geodetic Coordinates: Numeric Method
4. Parallax Effect Correction Error Simulation
- Prepare a grid of geodetic coordinates: , , with steps for each dimension;
- Transform the grid coordinates to the geostationary view coordinates system, , (from now on called the base , ) [27], and back to geodetic coordinates to specify which grid elements are out of scope; for out-of-scope elements, this operation will return Not a Number (NaN – floating point special value).
- For each , the following steps are performed:
- For each and and with , calculate the coordinates using Equation (1);
- Using , calculate the geostationary view coordinates and ;
- With , , and , run the correction algorithms: Vicente et al./Koenig, Vicente et al./Koenig augmented, and the numerical geodetic coordinates method;
- Each algorithm returns , , which should be transformed to , ;
- The distance between the simulated original base , and , in the geostationary view space will be denoted as the correction error.
- Algorithm: Levenberg–Marquardt (instead of Newton);
- Function tolerance: ;
- Specify objective gradient: yes;
- Input damping: .
5. Discussion
- Different nature of the acquisition model, as on-ground radar and MSG satellite acquisition are registered with a slight temporal shift (less than 15 min);
- Both sensors utilize the different physical natures of acquisition. The on-ground radar is an active sensor which sends out an electromagnetic signal in the microwave spectrum and measurers the echo intensity scattered from precipitation particles. On the contrary, MSG SEVIRI is a passive sensor that measures radiation in a particular electromagnetic bandwidth (visible and near visible spectrum) coming from the sun and thermal radiance;
- Data acquired by MSG and on-ground radar is also characterized by different spatial resolutions. Therefore, in order to compare these datasets, additional resampling needs to be performed.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaminski, L.; Kulawiak, M.; Cizmowski, W.; Chybicki, A.; Stepnowski, A.; Orlowski, A. Web-based GIS dedicated for marine environment surveillance and monitoring. In Proceedings of the OCEANS 2009-EUROPE, Bremen, Germany, 11–14 May 2009; pp. 1–7. [Google Scholar]
- Manzione, R.L.; Castrignano, A. A geostatistical approach for multi-source data fusion to predict water table depth. Sci. Total Environ. 2019, 696, UNSP 133763. [Google Scholar] [CrossRef] [PubMed]
- Mishra, M.; Dugesar, V.; Prudhviraju, K.N.; Patel, S.B.; Mohan, K. Precision mapping of boundaries of flood plain river basins using high-resolution satellite imagery: A case study of the Varuna river basin in Uttar Pradesh, India. J. Earth Syst. Sci. 2019, 128, 105. [Google Scholar] [CrossRef] [Green Version]
- Berezowski, T.; Wassen, M.; Szatylowicz, J.; Chormanski, J.; Ignar, S.; Batelaan, O.; Okruszko, T. Wetlands in flux: Looking for the drivers in a central European case. Wetl. Ecol. Manag. 2018, 26, 849–863. [Google Scholar] [CrossRef] [Green Version]
- Stateczny, A.; Bodus-Olkowska, I. Sensor data fusion techniques for environment modelling. In Proceedings of the 2015 16th International Radar Symposium (IRS), Bonn, Germany, 24–26 June 2015; pp. 1123–1128. [Google Scholar]
- Kazimierski, W.; Stateczny, A. Fusion of data from AIS and tracking radar for the needs of ECDIS. In Proceedings of the 2013 Signal Processing Symposium (SPS), Jachranka, Poland, 5–7 June 2013; pp. 1–6. [Google Scholar]
- Roebeling, R.A.; Holleman, I. SEVIRI rainfall retrieval and validation using weather radar observations. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Vicente, G.A.; Scofield, R.A.; Menzel, W.P. The Operational GOES Infrared Rainfall Estimation Technique. Bull. Amer. Meteor. Soc. 1998, 79, 1883–1898. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, X.; Zhang, J.; Zhao, H.; Song, Y. Higher temporal evapotranspiration estimation with improved SEBS model from geostationary meteorological satellite data. Sci. Rep. 2019, 9, 14981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henken, C.C.; Schmeits, M.J.; Deneke, H.; Roebeling, R.A. Using MSG-SEVIRI Cloud Physical Properties and Weather Radar Observations for the Detection of Cb/TCu Clouds. J. Appl. Meteor. Climatol. 2011, 50, 1587–1600. [Google Scholar] [CrossRef]
- Miller, S.D.; Rogers, M.A.; Haynes, J.M.; Sengupta, M.; Heidinger, A.K. Short-term solar irradiance forecasting via satellite/model coupling. Solar Energy 2018, 168, 102–117. [Google Scholar] [CrossRef]
- Li, S.; Sun, D.; Yu, Y. Automatic cloud-shadow removal from flood/standing water maps using MSG/SEVIRI imagery. Int. J. Remote Sens. 2013, 34, 5487–5502. [Google Scholar] [CrossRef]
- Wang, C.; Luo, Z.J.; Huang, X. Parallax correction in collocating CloudSat and Moderate Resolution Imaging Spectroradiometer (MODIS) observations: Method and application to convection study. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Feng, X.; Yang, C.; Chen, B. Improved Spatial Collocation and Parallax Correction Approaches for Calibration Accuracy Validation of Thermal Emissive Band on Geostationary Platform. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2647–2663. [Google Scholar] [CrossRef]
- Chen, J.; Yang, J.-G.; An, W.; Chen, Z.-J. An Attitude Jitter Correction Method for Multispectral Parallax Imagery Based on Compressive Sensing. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1903–1907. [Google Scholar] [CrossRef]
- Frantz, D.; Haß, E.; Uhl, A.; Stoffels, J.; Hill, J. Improvement of the Fmask algorithm for Sentinel-2 images: Separating clouds from bright surfaces based on parallax effects. Remote Sens. Environ. 2018, 215, 471–481. [Google Scholar] [CrossRef]
- Roebeling, R.A.; Feijt, A.J. Validation of cloud liquid water path retrievals from SEVIRI on METEOSAT-8 using CLOUDNET observations. In Proceedings of the EUMETSAT Meteorological Satellite Conference, Helsinki, Finland, 12–16 June 2006; EUMETSAT: Darmstadt, Germany, 2006; pp. 12–16. [Google Scholar]
- Roebeling, R.A.; Deneke, H.M.; Feijt, A.J. Validation of Cloud Liquid Water Path Retrievals from SEVIRI Using One Year of CloudNET Observations. J. Appl. Meteor. Climatol. 2008, 47, 206–222. [Google Scholar] [CrossRef]
- Greuell, W.; Roebeling, R.A. Toward a Standard Procedure for Validation of Satellite-Derived Cloud Liquid Water Path: A Study with SEVIRI Data. J. Appl. Meteor. Climatol. 2009, 48, 1575–1590. [Google Scholar] [CrossRef] [Green Version]
- Schutgens, N.A.J.; Greuell, W.; Roebeling, R. Effect of inhomogeneity on the validation of SEVIRI LWP. In Current Problems in Atmospheric Radiation (irs 2008); Nakajima, T., Yamasoe, M.A., Eds.; Amer Inst Physics: New York, NY, USA, 2009; Volume 1100, p. 424. ISBN 978-0-7354-0635-3. [Google Scholar]
- Vicente, G.A.; Davenport, J.C.; Scofield, R.A. The role of orographic and parallax corrections on real time high resolution satellite rainfall rate distribution. Int. J. Remote Sens. 2002, 23, 221–230. [Google Scholar] [CrossRef]
- Koenig, M. Description of the parallax correction functionality. Available online: https://cwg.eumetsat.int/parallax-corrections/ (accessed on 17 January 2020).
- Wolfgang, T. Geodesy, An Introduction; De Gruyter: Berlin, Germany, 1980; ISBN 3-11-007232-7. [Google Scholar]
- Czarnecki, K. Geodezja współczesna; Wyd. 3 (1 w WN PWN)-1 dodruk; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2015; ISBN 978-83-01-18380-6. [Google Scholar]
- Meteorological Products Extraction Facility Algorithm Specification Document. Available online: https://www.eumetsat.int/website/wcm/idc/idcplg?IdcService=GET_FILE&dDocName=PDF_TEN_SPE_04022_MSG_MPEF&RevisionSelectionMethod=LatestReleased&Rendition=Web (accessed on 28 November 2019).
- Solve System of Nonlinear Equations - MATLAB Fsolve. Available online: https://www.mathworks.com/help/optim/ug/fsolve.html (accessed on 23 October 2019).
- Wolf, R. Coordination Group for Meteorological Satellites LRIT/HRIT Global Specification. Available online: https://www.cgms-info.org/documents/pdf_cgms_03.pdf (accessed on 28 November 2019).
- PROJ contributors. PROJ Coordinate Transformation Software Library; Open Source Geospatial Foundation: Beaverton, OR, USA, 2019. [Google Scholar]
- Marshall, J.S.; Gunn, K.L.S. Measurement of snow parameters by radar. J. Meteor. 1952, 9, 322–327. [Google Scholar] [CrossRef] [Green Version]
- Roebeling, R.A.; Feijt, A.J.; Stammes, P. Cloud property retrievals for climate monitoring: Implications of differences between Spinning Enhanced Visible and Infrared Imager (SEVIRI) on METEOSAT-8 and Advanced Very High Resolution Radiometer (AVHRR) on NOAA-17. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Optimal Cloud Analysis: Product Guide. Available online: http://www.eumetsat.int/website/wcm/idc/idcplg?IdcService=GET_FILE&dDocName=PDF_DMT_770106&RevisionSelectionMethod=LatestReleased&Rendition=Web (accessed on 8 January 2020).
- MSG Level 1. Available online: http://www.eumetsat.int/website/wcm/idc/idcplg?IdcService=GET_FILE&dDocName=PDF_TEN_05105_MSG_IMG_DATA&RevisionSelectionMethod=LatestReleased&Rendition=Web (accessed on 28 November 2019).
- GOES N Databook. Available online: https://goes.gsfc.nasa.gov/text/GOES-N_Databook/databook.pdf (accessed on 29 November 2019).
- MTG FCI L1 Product User Guide. Available online: http://www.eumetsat.int/website/wcm/idc/idcplg?IdcService=GET_FILE&dDocName=PDF_DMT_719113&RevisionSelectionMethod=LatestReleased&Rendition=Web (accessed on 28 November 2019).
- Hewison, T.J. An Evaluation of the Uncertainty of the GSICS SEVIRI-IASI Intercalibration Products. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1171–1181. [Google Scholar] [CrossRef]












| City | Geodetic Coordinates | Displacement Sensitivity as in Equation (32) |
|---|---|---|
| Cape Town | 33.9253° S 18.4239° E | 0.667 |
| Madrid | 40.4177° N 3.6947° W | 0.696 |
| Brasília | 15.7839° S 47.9142° W | 0.784 |
| Gdańsk | 54.3475° N 18.6453° E | 0.827 |
| Tromsø | 69.6667° N 18.9333° E | 0.868 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bieliński, T. A Parallax Shift Effect Correction Based on Cloud Height for Geostationary Satellites and Radar Observations. Remote Sens. 2020, 12, 365. https://doi.org/10.3390/rs12030365
Bieliński T. A Parallax Shift Effect Correction Based on Cloud Height for Geostationary Satellites and Radar Observations. Remote Sensing. 2020; 12(3):365. https://doi.org/10.3390/rs12030365
Chicago/Turabian StyleBieliński, Tomasz. 2020. "A Parallax Shift Effect Correction Based on Cloud Height for Geostationary Satellites and Radar Observations" Remote Sensing 12, no. 3: 365. https://doi.org/10.3390/rs12030365
APA StyleBieliński, T. (2020). A Parallax Shift Effect Correction Based on Cloud Height for Geostationary Satellites and Radar Observations. Remote Sensing, 12(3), 365. https://doi.org/10.3390/rs12030365