A Refined SNR Based Stochastic Model to Reduce Site-Dependent Effects
Abstract
:1. Introduction
2. Data Description
3. The Refined SNR Based Stochastic Modelling Method
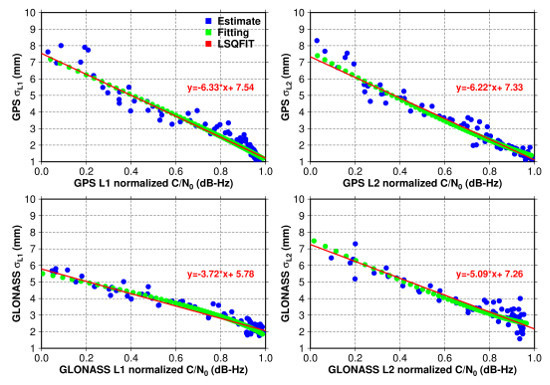
3.1. GPS/GLONASS SNR Measurements Analysis
3.2. The Refined SNR Based Stochastic Model
3.3. The Flow Chart of the Refined SNR Based Stochastic Model and the Application Strategy
4. Experiments and Results
4.1. Assessment of Station Observation Environment
4.2. Bridge Monitoring Experiment Analysis
4.3. Ambiguity Resolution Performance Analysis
4.4. The Positioning Performance Analysis
5. Discussion
6. Conclusions
- Obvious different patterns can be observed in the GLONASS elevation-dependent SNR time series of Leica receivers. However, the phase precision has no different pattern features. That means the values of GLONASS SNR data cannot be applied to weight the phase observation directly.
- A normalized method is proposed to process the GNSS SNR data and a linear relationship between the normalized SNR data and the precision of phase observations in dual-frequency observations of GPS and GLONASS system can be observed for LEICA receivers. Hence, a linear SNR based stochastic model can be established, which is appropriate to show a precision sky-plot for assessing the site observation environment.
- Compared with the empirical elevation and SNR dependent stochastic models, and even the realistic elevation model, the refined SNR based stochastic model proposed in this paper shows the highest integer ambiguity resolution success rate in the data processing. The noise level in the data processing time series caused by obstructions can be significantly reduced with the proposed stochastic model.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Deng, C.; Tang, W.; Liu, J.; Shi, C. Reliable Single-Epoch Ambiguity Resolution for Short Baselines Using Combined GPS/BeiDou System. GPS Solut. 2014, 18, 375–386. [Google Scholar] [CrossRef]
- Meng, X.; Nguyen, D.; Xie, Y.; Owen, J.; Psimoulis, P.; Ince, S.; Chen, Q.; Ye, J.; Bhatia, P. Design and Implementation of a New System for Large Bridge Monitoring—GeoSHM. Sensors 2018, 18, 775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, W.; Xi, R.; Chen, H.; Xiao, Y. Accuracy Analysis of Continuous Deformation Monitoring Using BeiDou Navigation Satellite System at Middle and High Latitudes in China. Adv. Space Res. 2017, 59, 843–857. [Google Scholar] [CrossRef]
- Xi, R.; Chen, H.; Meng, X.; Jiang, W.; Chen, Q. Reliable Dynamic Monitoring of Bridges with Integrated GPS and BeiDou. J. Surv. Eng. 2018, 144, 04018008. [Google Scholar] [CrossRef]
- Meng, X.; Roberts, G.W.; Dodson, A.H.; Cosser, E.; Barnes, J.; Rizos, C. Impact of GPS Satellite and Pseudolite Geometry on Structural Deformation Monitoring: Analytical and Empirical Studies. J. Geod. 2004, 77, 809–822. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Dynamic Multipath in Structural Bridge Monitoring: An Experimental Approach. GPS Solut. 2014, 18, 209–218. [Google Scholar] [CrossRef]
- Zimmermann, F.; Eling, C.; Kuhlmann, H. Empirical Assessment of Obstruction Adaptive Elevation Masks to Mitigate Site-Dependent Effects. GPS Solut. 2017, 21, 1695–1706. [Google Scholar] [CrossRef]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of Multipath Effect in GNSS Short Baseline Positioning by the Multipath Hemispherical Map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R.; Jazaeri, S.; Zangeneh-Nejad, F.; Asgari, J. Role of Stochastic Model on GPS Integer Ambiguity Resolution Success Rate. GPS Solut. 2016, 20, 51–61. [Google Scholar] [CrossRef]
- Li, B. Stochastic Modeling of Triple-Frequency BeiDou Signals: Estimation, Assessment and Impact Analysis. J. Geod. 2016, 90, 593–610. [Google Scholar] [CrossRef]
- Li, B.; Zhang, L.; Verhagen, S. Impacts of BeiDou Stochastic Model on Reliability: Overall Test, w-Test and Minimal Detectable Bias. GPS Solut. 2017, 21, 1095–1112. [Google Scholar] [CrossRef]
- Luo, X.; Mayer, M.; Heck, B. Improving the Stochastic Model of GNSS Observations by Means of SNR-Based Weighting. In Observing our Changing Earth; Sideris, M.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 725–734. [Google Scholar]
- Agnew, D.C.; Larson, K.M. Finding the Repeat Times of the GPS Constellation. GPS Solut. 2006, 11, 71–76. [Google Scholar] [CrossRef]
- Atkins, C.; Ziebart, M. Effectiveness of Observation-Domain Sidereal Filtering for GPS Precise Point Positioning. GPS Solut. 2016, 20, 111–122. [Google Scholar] [CrossRef]
- Choi, K.; Bilich, A.; Larson, K.M.; Axelrad, P. Modified Sidereal Filtering: Implications for High-Rate GPS Positioning: HIGH-RATE GPS POSITIONING. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Bilich, A.; Axelrad, P. Improving the Precision of High-Rate GPS. J. Geophys. Res. 2007, 112, B05422. [Google Scholar] [CrossRef]
- Ragheb, A.E.; Clarke, P.J.; Edwards, S.J. GPS Sidereal Filtering: Coordinate- and Carrier-Phase-Level Strategies. J. Geod. 2007, 81, 325–335. [Google Scholar] [CrossRef]
- Wang, D.; Meng, X.; Gao, C.; Pan, S.; Chen, Q. Multipath Extraction and Mitigation for Bridge Deformation Monitoring Using a Single-Difference Model. Adv. Space Res. 2017, 60, 2882–2895. [Google Scholar] [CrossRef]
- Zhong, P.; Ding, X.; Yuan, L.; Xu, Y.; Kwok, K.; Chen, Y. Sidereal Filtering Based on Single Differences for Mitigating GPS Multipath Effects on Short Baselines. J. Geod. 2010, 84, 145–158. [Google Scholar] [CrossRef]
- Pugliano, G.; Robustelli, U.; Rossi, F.; Santamaria, R. A New Method for Specular and Diffuse Pseudorange Multipath Error Extraction Using Wavelet Analysis. GPS Solut. 2016, 20, 499–508. [Google Scholar] [CrossRef]
- Satirapod, C.; Rizos, C. Multipath Mitigation by Wavelet Analysis For GPS Base Station Applications. Surv. Rev. 2005, 38, 2–10. [Google Scholar] [CrossRef]
- Zhong, P.; Ding, X.L.; Zheng, D.W.; Chen, W.; Huang, D.F. Adaptive Wavelet Transform Based on Cross-Validation Method and Its Application to GPS Multipath Mitigation. GPS Solut. 2008, 12, 109–117. [Google Scholar] [CrossRef]
- Ge, L.; Chen, H.-Y.; Han, S.; Rizos, C. Adaptive Filtering of Continuous GPS Results. J. Geod. 2000, 74, 572–580. [Google Scholar] [CrossRef]
- Zheng, D.W.; Zhong, P.; Ding, X.L.; Chen, W. Filtering GPS Time-Series Using a Vondrak Filter and Cross-Validation. J. Geod. 2005, 79, 363–369. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Luo, X.; Knöpfler, A.; Mayer, M. Generating Statistically Robust Multipath Stacking Maps Using Congruent Cells. GPS Solut. 2015, 19, 83–92. [Google Scholar] [CrossRef]
- Moore, M.; Watson, C.; King, M.; McClusky, S.; Tregoning, P. Empirical Modelling of Site-Specific Errors in Continuous GPS Data. J. Geod. 2014, 88, 887–900. [Google Scholar] [CrossRef]
- Brunner, F.K.; Hartinger, H.; Troyer, L. GPS Signal Diffraction Modelling: The Stochastic SIGMA-δ Model. J. Geod. 1999, 73, 259–267. [Google Scholar] [CrossRef]
- Bilich, A.; Larson, K.M.; Axelrad, P. Modeling GPS Phase Multipath with SNR: Case Study from the Salar de Uyuni, Boliva. J. Geophys. Res. 2008, 113, B04401. [Google Scholar] [CrossRef]
- Benton, C.J.; Mitchell, C.N. Isolating the Multipath Component in GNSS Signal-to-Noise Data and Locating Reflecting Objects: ISOLATE GNSS MULTIPATH, LOCATE REFLECTOR. Radio Sci. 2011, 46. [Google Scholar] [CrossRef] [Green Version]
- Groves, P.D.; Jiang, Z. Height Aiding, C/N 0 Weighting and Consistency Checking for GNSS NLOS and Multipath Mitigation in Urban Areas. J. Navig. 2013, 66, 653–669. [Google Scholar] [CrossRef] [Green Version]
- Peyraud, S.; Bétaille, D.; Renault, S.; Ortiz, M.; Mougel, F.; Meizel, D.; Peyret, F. About Non-Line-of-Sight Satellite Detection and Exclusion in a 3D Map-Aided Localization Algorithm. Sensors 2013, 13, 829–847. [Google Scholar] [CrossRef] [Green Version]
- Lau, L.; Cross, P. Development and Testing of a New Ray-Tracing Approach to GNSS Carrier-Phase Multipath Modelling. J. Geod. 2007, 81, 713–732. [Google Scholar] [CrossRef]
- Groves, P.D.; Jiang, Z.; Wang, L.; Ziebart, M.K. Intelligent Urban Positioning Using Multi-Constellation GNSS with 3D Mapping and NLOS Signal Detection. In Proceedings of the 25th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 458–472. [Google Scholar]
- Groves, P.D.; Jiang, Z.; Rudi, M.; Strode, P. A Portfolio Approach to NLOS and Multipath Mitigation in Dense Urban Areas. In Proceedings of the 26th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2013), Nashville Convention Center, Nashville, TN, USA, 16–20 September 2013; pp. 3231–3247. [Google Scholar]
- Hsu, L.-T.; Jan, S.-S.; Groves, P.D.; Kubo, N. Multipath Mitigation and NLOS Detection Using Vector Tracking in Urban Environments. GPS Solut. 2015, 19, 249–262. [Google Scholar] [CrossRef]
- Strode, P.R.R.; Groves, P.D. GNSS Multipath Detection Using Three-Frequency Signal-to-Noise Measurements. GPS Solut. 2016, 20, 399–412. [Google Scholar] [CrossRef] [Green Version]
- Hartinger, H.; Brunner, F.K. Variances of GPS Phase Observations: The SIGMA-ɛ Model. GPS Solut. 1999, 2, 35–43. [Google Scholar] [CrossRef]
- Xi, R.; Meng, X.; Jiang, W.; An, X.; Chen, Q. GPS/GLONASS Carrier Phase Elevation-Dependent Stochastic Modelling Estimation and Its Application in Bridge Monitoring. Adv. Space Res. 2018, 62, 2566–2585. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Gamit Reference Manual: GPS Analysis at MIT, Release 10.4; CAMBRIDGE M A.Department of Earth, Atmospheric, and Planetary Sciences, Massachusset Institute of Technology: Cambridge, MA, USA, 2010. [Google Scholar]
- Pan, L.; Xiaohong, Z.; Fei, G. Ambiguity Resolved Precise Point Positioning with GPS and BeiDou. J. Geod. 2017, 91, 25–40. [Google Scholar] [CrossRef]
- Qian, K.; Wang, J.; Hu, B. A Posteriori Estimation of Stochastic Model for Multi-Sensor Integrated Inertial Kinematic Positioning and Navigation on Basis of Variance Component Estimation. J. Glob. Position. Syst. 2016, 14, 5. [Google Scholar] [CrossRef] [Green Version]
- Dai, W.; Ding, X.; Zhu, J. Comparing GPS Stochastic Models Based on Observation Quality Indices. Geomat. Inf. Sci. Wuhan Univ. 2008, 33, 718–722. [Google Scholar]


















| Model Names | Weighting Strategies |
|---|---|
| EEM (Elevation Empirical Model) | , a = b = 3 mm [39,40,41] |
| ERM (Elevation Refined Model) | [38] |
| SEM (SNR Empirical Model) | [42] |
| SRM (SNR Refined Model) | (Figure 4) |
| Station and Model | ASR for All Epochs (%) | ASR with Fixed WL Epochs (%) | Correctly-Fixed Rate (%) |
|---|---|---|---|
| SHM2 EEM | 99.13 | 99.65 | 100 |
| SHM2 ERM | 99.57 | 99.76 | 100 |
| SHM2 SRM | 99.64 | 99.77 | 100 |
| SHM4 EEM | 85.97 | 91.93 | 100 |
| SHM4 ERM | 90.33 | 92.45 | 100 |
| SHM4 SRM | 91.15 | 91.99 | 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, R.; Meng, X.; Jiang, W.; An, X.; He, Q.; Chen, Q. A Refined SNR Based Stochastic Model to Reduce Site-Dependent Effects. Remote Sens. 2020, 12, 493. https://doi.org/10.3390/rs12030493
Xi R, Meng X, Jiang W, An X, He Q, Chen Q. A Refined SNR Based Stochastic Model to Reduce Site-Dependent Effects. Remote Sensing. 2020; 12(3):493. https://doi.org/10.3390/rs12030493
Chicago/Turabian StyleXi, Ruijie, Xiaolin Meng, Weiping Jiang, Xiangdong An, Qiyi He, and Qusen Chen. 2020. "A Refined SNR Based Stochastic Model to Reduce Site-Dependent Effects" Remote Sensing 12, no. 3: 493. https://doi.org/10.3390/rs12030493
APA StyleXi, R., Meng, X., Jiang, W., An, X., He, Q., & Chen, Q. (2020). A Refined SNR Based Stochastic Model to Reduce Site-Dependent Effects. Remote Sensing, 12(3), 493. https://doi.org/10.3390/rs12030493