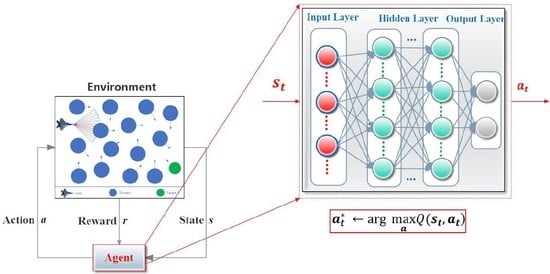
1. Introduction
Safe and reliable motion control for unmanned aerial vehicles (UAVs) is an open and challenging problem in the realm of autonomous robotics. Successfully flying from arbitrary departures to destinations, while avoiding ubiquitous threats without any human intervention is indeed essential for a UAV in many practical applications [
1,
2], such as search and rescue [
3], remote sensing [
4,
5], goods delivery [
6], and Destroy or Suppression of Enemy Air Defenses (DEAD/SEAD) [
7]. To maintain autonomous mobility, the UAV has to handle challenges in Observation, Orientation, Decision and Action (OODA) simultaneously, and these become particularly difficult while facing dynamic uncertain environments. Massive uncertain surroundings and unpredictable moving threats make any pre-planned motion strategy unavailable. Developing some novel techniques, which can provide the UAV robust motion strategies in these complex environments, becomes a crucial requirement in the near future.
Traditional approaches, such as A* [
8], RRT [
9], artificial potential fields [
10], simultaneously localization and mapping (SLAM) [
11], employ two steps to handle these motion control problems with unknown environments [
12]: (i) Perceive and estimate the environment state; and (ii) model and optimize the control command. These approaches are often susceptible to unforeseen disturbances, any incomplete perception, biased estimate, or inaccurate model will lead to poor performances [
13]. Their model-based scheme makes it difficult to apply such approaches to dynamic uncertain environments because the state transition models of the environments are usually unknown in those cases. Moreover, these traditional approaches use an open-loop mechanism [
14] that makes decisions without any reasoning of the future, and the decision process has to be executed repeatedly to compensate for the changes.
To overcome the limitations mentioned above, researchers have resorted to learning or adaptive approaches. Reinforcement learning (RL) [
15], for instance, can make agents learn the right actions to take with little or no prior knowledge of system model, and the predictive learning scheme makes it easily adapt to the stochastic changing conditions. For these reasons, RL has become a promising tool in improving autonomous flight in many different UAV applications. Junell [
16] modelled the Quadrotor guidance as a high-level reinforcement learning problem and successfully developed an autonomous flying test in an unknown environment. Luo [
17] proposed Deep-Sarsa, a novel path planning and obstacle avoidance approach, in order to navigate multi-UAVs fly autonomously in a dynamic environment. Imanberdiyev [
18] uses a model-based reinforcement learning algorithm, TEXPLORE, to solve the UAV autonomous navigation problem and demonstrate that the effect outperforms Q-learning based method. Since traditional RLs can only deal with discrete states, all of these researches have to simplify and limit the environment as a discrete grid, and this is different from the practical situation faced by UAVs. To maintain a better representation of the high-dimensional continuous state space, the deep neural network is introduced into the conventional RL and produces deep reinforcement learning (DRL) methods. A series of DRLs, such as Deep Q Network (DQN) [
19], Double DQN [
20], Dueling DQN [
21], and Prioritized DQN [
22] are proposed one after another, and some of them have been utilized in the field of UAV control and have achieved outstanding performance [
23,
24,
25,
26]. Kersandt [
24] establishes learning-based high-level controllers to navigate a UAV flying across a complicated environment with different DRL algorithms. Polvara [
25] learned a DQN-based intelligent controller and successfully controlled the UAV to land on moving platforms. Conde [
26] designed time-varying controllers with DQN to drive multiple UAVs and reach any formation as quickly as possible. However, these value-based DRLs have drawbacks, including that they can only address cases with discrete actions, which is the reason these applications only realized a discrete direction control of the UAV.
To achieve continuous control, policy gradient methods [
27] are introduced into DRL, which derive parameterized stochastic or deterministic policies with continuous actions by performing gradient descent in the parameter space. Silver [
28] proposed a deterministic policy gradient (DPG) algorithm, and demonstrated that it can significantly outperform the stochastic counterparts in high-dimensional action spaces. Lillicrap [
29] combined DQN and DPG within the actor-critic framework and produced a deep deterministic policy gradient (DDPG) algorithm, which can map continuous observations directly to continuous actions. While, DDPG may perform well sometimes, it is frequently brittle with respect to complete tasks, and challenges arise when DDPG is applied to solve UAV adaptive motion control problems. Firstly, UAV is sensitive to rapidly changing speed and adding speed control channel into DDPG will make the training process unstable. For this reason, most studies only take heading control channel into account [
25,
30,
31] in their UAV navigation tasks. This simplification limits their practical application scopes. Secondly, given the actor and critic are closely related in DDPG, an over-estimation of the critic will lead to policy vibrations in actors and the vibration will result in UAV’s frequent crash, while facing dynamic uncertain surroundings. Lastly, DDPG itself is susceptible to hyper-parameters and exploration schemes, any irrational setting can lead to unstable learning, which is the reason that region policy optimization is relied on (TRPO) [
32] and proximal policy optimization (PPO) [
33] algorithms are proposed. With respect to the motion control problem, the dynamic uncertain environment expands the state and action space, which increases the difficulties of exploration.
To address these challenges, we conducted some exploratory research and propose an improved DRL algorithm named Robust-DDPG. This new algorithm is used to provide the UAV robust motion control in dynamic uncertain environments. Specifically, we make the following contributions in this paper:
(1) We develop an actor-critic-based motion control framework, which can perform a dual-channel control of roll and speed, by predicting the desired steering angle and by reasoning the possible collision probability. The controller can provide safe flights for the UAV autonomously in dynamic uncertain environments.
(2) We propose an efficient policy-based DRL algorithm, Robust-DDPG, in which three critical tricks are introduced to provide a robust controller for the UAV. The first is a delayed-learning trick, in which the critic and actor networks are batch updated after each episode finishes, rather than being updated in each iteration. The second is an adversarial-attack trick, in which an adversarial scheme is introduced to sample noisy states and actions in the learning process. This trick will increase the robustness of the trained networks. The last is a mixed-exploration trick, in which rough sampling, based on -greedy and a fine sampling, based on Gaussian are performed in different periods of learning. By combining these three tricks, Robust-DDPG is able to overcome the shortcomings of DDPG and provide the UAV a controller with better adaptability to complicated, dynamic, and uncertain environments.
(3) We constructed a UAV mission platform to simulate dynamic stochastic environments for training and evaluating the effectiveness and robustness of our proposed methods. Through a series of experiments, we show that our trained UAV can adapt to various dynamic uncertain environments, with neither a map of the environment nor retraining or fine-tuning.
The remainder of this paper is organized as follows.
Section 2 introduces the UAV motion control problem and formulates it as an MDP.
Section 3 elaborates the core approach, Robust-DDPG, for problem solving, where three improved tricks, delayed learning, adversarial attack, and mixed exploration are integrated into an actor-critic framework. The performance, effectiveness, and adaptability of the proposed algorithm are demonstrated through a series of experiments in
Section 4.
Section 5 conducts a further discussion about the experimental results.
Section 6 concludes this paper and envisages some future work.
4. Results
This section presents experiments for evaluating the performance, the effectiveness and the adaptability of the proposed robust motion controller of the UAV through training experiments, exploiting experiments, and generalization experiments.
4.1. Experimental Platform and Settings
For the training and testing of the DRL-based motion controller, we construct a general simulation platform, depicted in
Figure 6. The platform simulates a world with a total size of 400
300 m
2 (the rectangular area) and a series of threats (the 24 white cylinders with different heights and sizes) are randomly scattered in the world. A certain proportion of the threats are set to move with stochastic velocities obey a uniform distribution U(1,6). A fixed-wing UAV (the blue entity) is required to fly across the unknown world until a specified target (the green circle) is finally reached. The UAV is supposed to fly at an altitude of 100 m and be equipped with a sensor that is capable of detecting an area of 40 m ahead (
) and
45 degrees from left to right (the blue sector in front of the UAV). Whenever an object is detected, the corresponding blue beams will be set to red so that the user can intuitively see the interaction between the UAV and the environment. The mobility of the UAV is limited by a maximum velocity
= 45 m/s and a maximum roll
. The motion uncertainty of the UAV is considered by defining disturbances
and
. The reward contribution rates are instantiated as
and
.
As described in
Section 3.1, two neural networks constitute the core of the controller, in which the critic is constructed by a 40
100
100
1 fully connected neural network and the actor owns a structure of 38
100
100
2. The observed states are normalized as a 38-dimensional input to the actor and the two-dimensional output actions are used to control the UAV’s motion. Adam optimizer is employed to learn network parameters with the same learning rate of
for the actor and critic. Other hyper-parameters are set with discount factor
, batch size
, experience pool
, target update interval
, and attack point
. In addition, the soft update tuning factor is
, the adversarial deep is
and the standard deviation is
. A descending
-greedy of
mixed with an
distribution is used to explore the action spaces, where
and
are set to provide a proper descending of
and
sets the lower bound of
.
and
are selected to generate temporally correlated explorations. Besides, the maximum episode length
is set to 1000.
4.2. Experiment I: Performance of Robust-DDPG
Before its exploitation, the DRL-based controller has to be trained first. To demonstrate the performance of the proposed Robust-DDPG, reasonable comparative experiments are necessary. To be specific, we resort to another two state-of-the-art DRLs, DQN, and DDPG, as baselines and re-implement them with almost the same hyper-parameter settings to Robust-DDPG. In DQN, we assume the UAV flies at a constant velocity of 20 m/s and simplify the control commands to
only. All three agents are trained with the same dynamic uncertain environment, depicted in
Figure 5. The experiments repeat 7000 episodes with 5000 episodes for learning and 2000 episodes for exploiting. In each episode, the UAV, target, and threats are randomly re-deployed throughout the world.
To measure the performance, we define some quantitative evaluation indicators: Hit rate, crash rate, lost rate, and average reward. For each agent, the hit rate, crash rate, and lost rate can be obtained by counting the percentage of successfully hitting the target over the latest 500 episodes, the percentage of crashing with threats over the last 500 episodes, and the percentage of trapped until that episode ends over the last 500 episodes, respectively. Average reward is defined as the mean value of the rewards per episode. Due to the severe fluctuation of average reward, we further average it every 500 episodes. The final learning results are illustrated in
Figure 7, including convergence curves of the hit rate (
Figure 7a) and the convergence curves of the average reward (
Figure 7b).
From
Figure 7, we can see: (1) Robust-DDPG uses about 2500 episodes to converge to a hit rate of about 92.6% and an average reward of about 1.8, while DDPG and DQN’s records are (episode, hit rate, average reward) = (4000, 88.7%, 1.4), and (5000, 82.4%, 1.0), respectively. In other words, Robust-DDPG achieves a faster convergence, a higher hit rate and a larger average reward comparing with the other two algorithms. This is because the delayed learning and mixed exploration techniques provide Robust-DDPG more efficient data utilization and more stable policy update. (2) In the exploiting stage (right part of the dotted line in
Figure 7a), the added motion disturbances cause significant decreases of the hit rates of DQN and DDPG, but not for Robust-DDPG. This good adaptability to uncertain environments comes from the adversarial attack technique used in Robust-DDPG. To make a more specific verification, we further count all the three indicators of hit rates, crash rates and lost rates of the different agents in different stages. All the results are arranged in
Table 1.
Obviously, Robust-DDPG achieves the best performance in all three algorithms. From the longitudinal point of view, Robust-DDPG brings (10.2%, 3.9%), (20.8%, 12.1%) increases of hit rates, brings (8.3%, 3.0%), (14.7%, 10.5%) decreases of crash rates, brings (1.9%, 0.9%), (6.1%, 1.6%) decreases of lost rates in learning and exploiting stages comparing to (DQN, DDPG), which means Robust-DDPG is more efficient than DQN and DDPG. From lateral direction, Robust-DDPG only brings 1.6% decrease of hit rate, while DQN and DDPG bring 12.2%, 9.8% decreases of hit rates, only brings 0.6% increase of crash rate, while DQN and DDPG bring 7.0%, 8.1% increases of crash rates, only brings 1% increase of lost rate, while DQN and DDPG bring 5.2%, 1.7% increases of lost rates in exploiting stage comparing to learning stage, which means Robust-DDPG is more robust than DQN and DDPG.
4.3. Experiment II: Effectiveness of Robust-DDPG
While learning is done, the controller is constructed. In this section, we conduct some UAV exploiting experiments and evaluate the effectiveness of the Robust-DDPG-based controller. Specifically, we let the three controllers constructed by DQN, DDPG, and Robust-DDPG drive a UAV to start from the same initial location (−10, 180), cross the same dynamic environment, and reach the target point (−120, −120). The exploiting environment here is more complicated than the one for learning as
Figure 6. We take three screenshots for each controller at T = 5 s, T = 10 s and the terminal time. All the screenshots can be seen in
Figure 8.
As we can see in
Figure 8, the three controllers fly out completely different trajectories for the same task. DQN flies at a constant speed (20 m/s) and selects a relatively safe path to bypassing the moving threats. At time 22.2 s, it successfully reaches the target and the UAV flies 463.2 m in total. For DDPG, it chooses to avoid intensive threat areas and flies around to maintain safety, which leads to a longer path of 651.1 m. However, by dynamically adjusting the flying speed, it only takes 15.1 s to complete the journey. To clearly show the changing in speed, we use arrows of different sizes to indicate different speeds. Zoom in the pictures in
Figure 8 and you will find the difference of the trajectories. Among the three controllers, Robust-DDPG flies the most efficient path. Through fine adjustments in the speed and roll, Robust-DDPG can safely avoid threats and fly quickly to the target. In fact, it only takes 11.4 s and flies 443.5 m to finally finish the task. Obviously, we can conclude that Robust-DDPG provides the most efficient controller, since it enables the UAV to complete the mission with minimum time and path costs. The exploiting effectiveness is intuitively shown in
Table 2.
4.4. Experiment III: Adaptability of Robust-DDPG
To further validate the Robust-DDPG can be generalized into more complex environments, we conduct a series of other exploiting experiments in this section. The experiments try to perform a comprehensive evaluation of Robust-DDPG’s adaptability to complicated, dynamic, and uncertain environments.
(a) Adaptability to complicated environments: we characterize environmental complexity by the density of threats (
Dens). We build a series of environments by increasing the density of threats (
Figure 9 illustrates three examples with threat density of 0.1, 0.3 and 0.5) and exploit the three learned agents to drive the UAV to fly in these environments. Each experiment is set to repeat 1000 episodes and each episode randomly re-deploys the UAV and target. The hit rate of the 1000 episodes will be counted after the end of each experiment.
Figure 10 depicts the trends of hit rates under different threat densities of the three agents. Obviously, the increasing threat density has caused declines of the hit rates of all the three agents, but Robust-DDPG has presented a slower and smaller decline comparing to DQN and DDPG. In fact, Robust-DDPG has stayed about a hit rate of 61.0% even in a highly complex environment (
dens = 0.5), while DQN and DDPG have dropped down to 22.9%, and 30.8%, respectively. In other words, Robust-DDPG shows greatest adaptability to complicated environments.
(b) Adaptability to dynamic environments: We use the proportion of moving threats (
Pro) among all threats to characterize the dynamics of the environment.
Pro = 0 means all the threats are stationary, while
Pro = 1 means all of them are movable. The speeds of the moving threats are randomly sampled from a uniform distribution U(5, 10). In the experiments, we gradually increase Pro from 0 to 1 and examine the hit rate trend of the three agents. As illustrated in
Figure 11, Robust-DDPG provides better adaptability to dynamic environments. As the proportion of moving threats increases from 0 to 1, Robust-DDPG still reaches a hit rate of nearly 66.0% after a slow decline, while DQN and DDPG dropped rapidly from 88.7% and 90.1% to 28.4% and 41.7%. Robust-DDPG can provide a more stable policy for the UAV control, due to proposed three tricks in this paper.
(c) Adaptability to uncertain environments: We increase the uncertainty of the environments by adding noises to the motion of UAV and further explore the Robust-DDPG’s adaptability to these environments. Noise intensity can be represented by disturbances
and
in Equation (1). So we conduct a series of comparative experiments by gradually increasing the values of
and
, and then evaluate the impact of noise with different intensity on the hit rate. The trends of hit rates under different noise intensities of the three agents are illustrated in
Figure 12. As we can see, Robust-DDPG performs great adaptability to uncertain environments, because as
and
increase from 0 to 30, the hit rate only decreases from 93.7% to 74.1%. This is mainly due to the adversarial attacks during the training process. In contrast, DQN and DDPG present worse robustness to uncertain environments that when the noise intensities increase, larger decreases of the hit rates occur.
5. Discussion
For a comprehensive evaluation of the proposed algorithm, Robust-DDPG, experiments are conducted to verify its training performance, exploiting effectiveness, and environmental adaptability, by comparing it to DQN and DDPG algorithms. Most of the hyper-parameters are tuned by extensive repeated trials and some of them are selected based on domain experience. With respect to the same parameters, three different models are trained and tested in a series of repetitive experiments.
For the training performance evaluation, Robust-DDPG converges to a hit rate of approximate 92.6% in about 2500 episodes, while DQN uses about 5000 episodes to converge to a hit rate of 82.4% and DDPG uses about 4000 episodes to converge to a hit rate of 88.7%. In other words, Robust-DDPG converges to a higher final hit rate with less training time. The great improvements in convergence speed and convergence performance come from the joint work of the mixed exploration trick and the delayed learning trick described in
Section 3.2.1 and
Section 3.2.3. The former ensures sample diversity in the early learning stage and provide Robust-DDPG more efficient data utilization. The latter keeps the learning in a stable strategic direction and improves the opportunity of learning a better policy.
For the exploiting effectiveness evaluation, the UAV is driven by three controllers to fly from the same departure, across the same dynamic environment, and to the same destination, respectively. The result is Robust-DDPG-based controller flies the most efficient path, that is, the shortest flight time of 11.4 s and the shortest path length of 443.5 m. Comparing the tracks of the three UAVs (in
Figure 8), we can see that the control commands provided by Robust-DDPG-based controller perform a better fit between the speed and roll channel. Neither is it as radical as DDPG that flies with high speed and large roll, nor is it as cautious as DQN, which flies with constant low speed and small roll, it just fine-tunes both the speed and roll dynamically according to the sensed environment. This outstanding effectiveness of Robust-DDPG derives from the delayed learning trick. As we described in
Section 3.2.1, delayed learning trick ensures the actor and the critic to obey the same principle in an ongoing learning episode and avoids frequent swinging of strategic direction between radical policy and cautious policy. It is a significant trick for learning a reliable policy.
For the environmental adaptability evaluation, there are three sets of experiments. Firstly, we studied the trends of hit rates under different threat densities, and the results clearly show that Robust-DDPG owns better adaptability to complicated environments than DQN and DDPG. As
Figure 10 illustrates the smallest decent slop of hit rate for Robust-DDPG. Similarly, the trends of hit rates under different moving threat proportions and the trends of hit rates under different noise intensities are explored, and the results in
Figure 11 and
Figure 12 leads to the same conclusion, and Robust-DDPG owns better adaptability to dynamic and uncertain environments than DQN and DDPG. Better adaptability means Robust-DDPG can be generalized into more complex environments. This feature is contributed by all the three tricks proposed in this paper, especially the adversarial attack trick. Introducing some adversarial attacks into the training process, the agent learns some additional skills that could be used to handle newly emerged circumstances.
In order to eliminate the impacts of accidental factors, we further carry out some statistical significance tests based on the original data used in
Figure 10,
Figure 11 and
Figure 12. As the data hardly satisfies normality and variance homogeneity, Friedman test is finally used. For simplification, let
A,
B and
C denotes Robust-DDPG, DDPG, and DQN, respectively. To highlight the advantages of Robust-DDPG, we conduct
Friedman(
A,
B),
Friedman(
A,
C), and
Friedman(
A,
B,
C) to assess whether the differences between
A and
B;
A and
C;
A,B and
C are really significant. The basic Hypothesis is the difference is not significant. From the test results shown in
Table 3, we can see that the condition
p < 0.05 occurs in all test, which means the Hypothesis has to be rejected. In other words, the differences between Robust-DDPG and DDPG; Robust-DDPG and DQN; Robust-DDPG, DDPG and DQN are all significant. Robust-DDPG does have better adaptability than DDPG and DQN.
From all the experimental results, we conclude that Robust-DDPG performs great advantages in t learning performance, exploiting effectiveness, and environmental adaptability. It is a powerful weapon to provide the UAV great capabilities of autonomous flying in complex environments. However, it is worth mentioning that despite of our efforts in the robustness and adaptation, there are still challenges, while trying to transfer this technique to a real UAV application. In the context of real control, the uncertainty is everywhere and exists all the time, the positioning error, the sensing error, the actuator error or even the crosswind, etc. No matter how well the controller is trained in virtual environment, the reality gap does exist. It is still difficult to figure out in what range of uncertainty the controller can operate safely before adaptation is necessary. It needs some trial and errors with a real UAV. We can characterize as much uncertainty as possible by maintaining insight into flight control system, understand the techniques, and model them in the virtual environment. By constantly reducing the reality gap, we will finally apply this technique in a real UAV platform.