Comparison of the Remapping Algorithms for the Advanced Technology Microwave Sounder (ATMS)

Abstract

One of the limitations in using spaceborne, microwave radiometer data for atmospheric remote sensing is the nonuniform spatial resolution. Remapping algorithms can be applied to the data to ameliorate this limitation. In this paper, two remapping algorithms, the Backus–Gilbert inversion (BGI) technique and the filter algorithm (AFA), widely used in the operational data preprocessing of the Advanced Technology Microwave Sounder (ATMS), are investigated. The algorithms are compared using simulations and actual ATMS data. Results show that both algorithms can effectively enhance or degrade the resolution of the data. The BGI has a higher remapping accuracy than the AFA. It outperforms the AFA by producing less bias around coastlines and hurricane centers where the signal changes sharply. It shows no obvious bias around the scan ends where the AFA has a noticeable positive bias in the resolution-enhanced image. However, the BGI achieves the resolution enhancement at the expense of increasing the noise by 0.5 K. The use of the antenna pattern instead of the point spread function in the algorithm causes the persistent bias found in the AFA-remapped image, leading not only to an inaccurate antenna temperature expression but also to the neglect of the geometric deformation of the along-scan field-of-views.

1. Introduction

Microwave radiometers have wide applications in atmospheric remote sensing and provide essential inputs to numerical weather prediction models [1,2]. However, the application of these spaceborne, multispectral measurements from multiple sensors is often plagued with the problem of nonuniform spatial resolution caused by the limited size of the satellite instrument antenna and the frequency-dependent microwave emission from the earth–atmosphere system. The mismatch in resolution becomes a critical issue when observations from different frequencies and different sensors are combined to retrieve geophysical parameters like wind speed, cloud liquid water, total precipitation water, and snow depth [3,4,5,6]. It could also lead to uncertainty in the cross-calibration between similar satellite radiometer instruments [2,4,7,8].

To solve this problem, much effort has been made to manipulate the resolution of measurements from various sources, e.g., the Backus–Gilbert inversion (BGI) method [9,10,11,12,13,14,15,16], various filter algorithms [17,18,19], the truncated singular value decomposition method [20,21], and the scatterometer image-reconstruction algorithm [13,22,23]. Recently, many deep-learning-based super-resolution technologies have been proposed to improve the image quality of the natural environment [24,25,26,27,28,29]. Since the development by Hu et al. [30] of a deconvolution algorithm based on a convolutional neural network, the deep learning technique has been applied to microwave radiometer data to enhance their resolution [31,32,33]. However, among these algorithms, only a few manage to match the intrinsic antenna pattern of the observations. These algorithms are the focus of this study. These remapping techniques take advantage of the extra information provided by the overlaps between adjacent fields-of-view (FOVs) to produce observations with the expected antenna pattern. The result is an estimate of the antenna temperature (Ta) distribution the sensor would have measured, given a prescribed antenna pattern that is different from the actual one.

Currently available remapping algorithms for microwave sensors can be categorized as spatial-domain-based methods and frequency-domain-based methods. The BGI method represents the former. First developed by Backus and Gilbert [34,35] for solving integration equations, Stogryn [9] then applied the method to enhance the spatial resolution or reduce observations from spaceborne microwave instruments. Since then, the BGI method has been widely used as a remapping algorithm for multi-frequency microwave radiometers, such as the Special Sensor Microwave/Imager, the Microwave Radiation Imager, and the Advanced Technology Microwave Sounder (ATMS), among other instruments [11,12,15,16]. This method has been implemented in the ATMS resampling algorithm to produce ATMS brightness temperatures (Tbs) at each Cross-track Infrared Sounder FOV [36]. The filter algorithm represents the frequency-domain-based technique. Its theory is similar to frequency-domain-based deconvolution algorithms [17,18]. They both remove the impact of the original antenna pattern through deconvolution in the frequency domain. The filter algorithm for remapping does one more step of adding the influence of a target antenna pattern to the datasets in the same way. Hu et al. [33] used a similar method to generate high-resolution and low-resolution data pairs for training a deep learning residual network. Zou and Tian [6] used this algorithm to process ATMS data for hurricane warm-core retrievals. The filter algorithm was also applied in the ATOVS and AVHRR Pre-processing Package (AAPP) to remap ATMS data to Advanced Microwave Sounding Unit-A (AMSU-A)-like FOVs [37]. Hereafter, the filter algorithm will be called the AAPP Filter Algorithm (AFA). Although the BGI and the AFA have long been adopted in operational ATMS data pre-processing, and the remapped dataset is widely used by the scientific community, their strengths and weaknesses have never been compared.

This paper is devoted to the analysis and evaluation of these two remapping algorithms. For this purpose, the algorithms are applied to produce AMSU-A-like data from ATMS observations using both simulated and actual ATMS datasets. This paper is organized as follows. In Section 2, after a brief introduction to ATMS and AMSU-A instrument characteristics, descriptions of the BGI and AFA algorithms follow. Section 3 shows the point spread function (PSF) reconstructed by the BGI algorithm, which helps to understand some of the simulation results presented in this section. A comparison of the algorithms using actual ATMS data is also provided. Section 4 presents a discussion, and conclusions are made in Section 5.

2. Materials and Methods

2.1. ATMS and AMSU-A/MHS Instruments and Scan Geometries

The ATMS and AMSU-A/Microwave Humidity Sounder (MHS) are both cross-track scanning microwave sensors onboard the NOAA and MetOp series of polar-orbiting satellites, providing measurements of atmospheric thermal emission in the microwave region between 23 and 183 GHz. As a successor to and a combination of AMSU-A/MHS, the ATMS inherits most of its channels from its predecessor. ATMS channels 1–16 at frequencies ranging from 23 to 88 GHz are close to the AMSU-A channels, except that channel 4 at 51.76 GHz is a newly added ATMS channel, providing temperature information about the lower troposphere. ATMS samples have beam widths of 5.2° at 23 GHz and 31 GHz and 2.2° at the temperature-sounding channels. The beam widths of AMSU-A channels are all 3.3°. The ATMS channels located near the 183 GHz water vapor absorption line are similar to the MHS channels, except that channel 19 at 183.31 ± 4.5 GHz and channel 21 at 183.31 ± 1.8 GHz are new additions to the ATMS for better profiling atmospheric moisture. All channels of the two sensors operate with the same beam width of 1.1°. Therefore, by unifying the beam widths of AMSU-A and ATMS, their observations can be combined for studies of geophysical parameters and global climate changes.

The two sensors have different scan geometries. The ATMS has 96 scene resolution cells sampled at an interval of 8/3 s for each scan to cover 52.725° scan angles on both sides of the subsatellite path. By contrast, the AMSU-A scans the earth scene within ±49.5° of the nadir direction and has 30 FOVs. The larger scan angle of the ATMS creates a 2600 km swath width, which is larger than its predecessor AMSU-A (2343 km) and leaves almost no gaps near the equator, providing nearly full coverage of the low latitudes. The integration time for all ATMS channels is 18 ms, while that for AMSU-A channels 1–2 and 3–15 are 165 ms and 158 ms, respectively. Due to the shorter integration time, leading to a higher sampling rate, significant overlaps occur between the neighboring FOVs and between the neighboring scan lines of ATMS channels 1–16, but there is no overlap for AMSU-A FOVs. The oversampling feature of the ATMS allows for remapping the raw ATMS datasets to the observations with the AMSU-A-like antenna pattern. Because of the shorter integration time, the ATMS noise equivalent differential temperature (NEDT) is also larger than the corresponding AMSU-A channels. The comparison of the two sensors is well-documented in [38].

Note that due to the cross-scanning manner of the sensors and the curvature of the earth’s surface, the relative geometries of the data samples change over the scan. Figure 1a–b shows the ATMS channel-1 FOV (5.2° beam width) and the expected AMSU-A-like FOV (3.3° beam width) at nadir and at the scan edge, respectively. The beam width narrows when remapping from the ATMS channel-1 FOV to the AMSU-A-like FOV, referred to as resolution enhancement. Figure 1c–d shows the ATMS channel-3 FOV (2.2° beam width) and the AMSU-A-like FOV at nadir and scan ends, respectively. The beam width widens when remapping from the ATMS channel-3 FOV to the AMSU-A-like FOV, referred to as resolution degradation. Figure 1 illustrates that the relative geometries of the samples change significantly along the scan. Because the remapping algorithms are highly dependent on the overlaps between the raw antenna pattern and the expected one, the geometric deformation of the FOVs over the scan has a very important effect on the remapping algorithms [17,30,31,32].

2.2. ATMS Remapping Algorithms

This section describes the principles behind the BGI and AFA remapping algorithms. Since the beam widths of the ATMS channels 1 and 3 are broad compared with the sampling distance, the scan-motion smearing caused by the continuous scan mode of the ATMS is neglected to simplify the problem [37]. Based on this assumption, the Ta at location ${\rho }_0$ can be expressed as the convolution of the scene Tb with the antenna gain function G (normalized so that ${{\displaystyle \int }}_{4\pi }^{}Gd\mathsf{\Omega }=1$):

$$Ta\left({\rho }_0\right)={\displaystyle \int }Tb\left(\rho \right)·G\left({\rho }_0,\rho \right)dA$$

(1)

Note that the above integration requires that the variables Ta, Tb, and G are distributed on the same grids. Therefore, to be consistent with measurements, the antenna pattern needs to be projected onto the earth’s surface to generate the PSF.

2.2.1. Backus–Gilbert Inversion Algorithm

The BGI algorithm is a matrix inversion method for solving integral equations. In this algorithm, a set of optimal coefficients $a_{ij}$ is derived for generating Ta with the expected antenna pattern at the location ${\rho }_0$ ($T{a}_{target}\left({\rho }_0\right)$) as a linear combination of $n\times n$ numbers of adjacent original Tas at locations ${\rho }_{ij}$ ($T{a}_{source}\left({\rho }_{ij}\right)$):

$$T{a}_{target}\left({\rho }_0\right)={\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{j=1}^n{a}_{ij}T{a}_{source}\left({\rho }_{ij}\right)$$

(2)

For definiteness, consider a $n\times n$ window stretching in the along-track and cross-track directions with $T{a}_{target}$ at the center. Figure 1 shows the configuration. With the original gain function $G_{source}$, the variable $T{a}_{source}\left({\rho }_{ij}\right)$ in Equation (2) can be expressed as Equation (1):

$$T{a}_{target}\left({\rho }_0\right)={\displaystyle \int }\left({\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{j=1}^n{a}_{ij}{G}_{source}\left({\rho }_{ij},\rho \right)\right)Tb\left(\rho \right)dA$$

(3)

Comparing Equation (3) to Equation (1), the set of coefficients $a_{ij}$ makes the bracketed term in Equation (3) appear like the target gain function $G_{target}\left({\rho }_0,\rho \right)$. To obtain a tradeoff between the resolution enhancement and the noise suppression, optimal coefficients $a_{ij}$ are derived by minimizing the following objective function:

$$Q=Q_0\cos \gamma +e^{2}w\sin \gamma$$

(4a)

$$where Q_0={\displaystyle \int }({\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{j=1}^n{a}_{ij}{G}_{source}\left({\rho }_{ij},\rho \right)-G_{target}\left({\rho }_0,\rho \right){)}^{2}dA$$

(4b)

$$e^2={\left(∆T_{rms}\right)}^2{\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{j=1}^n{a}_{ij}^2$$

(4c)

where $∆T_{rms}$ is the channel noise in terms of NEDT, w is a scale factor used to make the terms on the right side of Equation (4a) dimensionally and numerically compatible, and $\gamma$ is a tradeoff factor that places degrees of emphasis on either the resolution enhancement or the noise suppression in the estimates of $T{a}_{target}$. Adjustable parameters are the window size n, w, and $\gamma$. These parameters have already been optimized in [16], where w is set to 0.001, n is set to $3\times 3$ for resolution enhancement and $5\times 5$ for resolution degradation, and $\gamma$ is tuned for each FOV position to make the sum of the coefficients equal to 1. Because the resolution degradation does not amplify the noise as the resolution enhancement does, $\gamma$ is set to zero in this case. These setups are used in this study. For reader completeness, the authors in [9,13] discuss some different criteria for selecting the parameters. Figure 1 shows the overlaps among the target FOV and the original FOVs within the selected calculation window.

The BGI algorithm in this study closely follows the one developed by Yang et al. [16], in which the antenna pattern is projected onto the earth’s surface, and the FOV deformation over the scan is taken into account by deriving a set of coefficients for each FOV position. One improvement made here is that the real antenna pattern, instead of the assumption of a Gaussian beam, is used in this algorithm. During a prelaunch ground test, antenna gain functions for 22 channels were measured at a resolution of 0.01° in an elevation angle and at intervals of 45° in azimuth angle at FOVs 1, 48, and 96 [39]. The antenna patterns at certain zenith and azimuthal angles at a certain FOV position are interpolated from the measurements through bilinear interpolation. Because the real AMSU-A antenna pattern is not available, a one-dimensional Gaussian function is adopted to approximate its gain function.

2.2.2. AAPP Filter Algorithm

The filter algorithm implemented in the AAPP manipulates the antenna pattern in the frequency domain [37]. Based on the convolution theorem, the expression of Ta in the spatial domain can be simplified to a multiplication in the frequency domain. Thus, the Fourier-space equivalent of Equation (1) can be written as

$$\widehat{Ta}\left(\xi \right)=\widehat{Tb}\left(\xi \right)·\widehat{G}\left(\xi \right)$$

(5)

where $\xi$ represents frequency, and the superscript $\widehat{}$ indicates the Fourier transform.

In the AAPP, the ATMS antenna gain function is approximated by a one-dimensional Gaussian function and its Fourier transform can be easily obtained. Let ${\widehat{G}}_{source}\left(\xi \right)$ and ${\widehat{G}}_{target}\left(\xi \right)$ be the Fourier transforms of the original and expected gain functions, respectively. In the frequency domain, the AFA can easily manipulate the beam width by first dividing the original antenna pattern and then multiplying the target one:

$${\widehat{Ta}}_{target}\left(\xi \right)={\widehat{Ta}}_{source}\left(\xi \right)·\frac{{\widehat{G}}_{target}\left(\xi \right)}{{\widehat{G}}_{source}\left(\xi \right)}$$

(6)

The second term on the right side of the equation is called the manipulating term. For resolution enhancement, to suppress the noise level, a cutoff factor c is added to attenuate the high-frequency components in the signal. With the cutoff factor c, the manipulating term takes the following form:

$$\frac{{\widehat{G}}_{target}\left(\xi \right)}{{\widehat{G}}_{original}\left(\xi \right)}·\exp \left(-\frac{{\left(\ln {\widehat{G}}_{target}\left(\xi \right)\right)}^2\ln 2}{{(\ln c)}^2}\right)$$

(7)

In the AAPP, c is set to 0.4 for the remapping from beam width 5.2° to 3.3°, based on experimental results.

After the beam width is manipulated in the frequency domain, ${\widehat{Ta}}_{target}\left(\xi \right)$ is transformed back to the spatial domain. The whole remapping process is now complete. This study uses the remapping codes implemented in the latest version of the AAPP, i.e., AAPP v8.5, released in December 2019. It includes the software atms_beamwidth.F, modify_beamwidth.F, and the parameter file atms_beamwidth.dat.

Note that unlike the BGI in which Equation (1) is strictly carried out on rectangular grids on the earth’s surface, the AFA works out this integration in the antenna-viewing coordinate system, assuming that the antenna pattern is a one-dimensional Gaussian function, and the observations are distributed evenly with the sampling distance 1.11°. Since Equation (1) uses the antenna pattern instead of its projection on Earth, not considered in this algorithm is the along-scan FOV deformation. In terms of computational efficiency, the BGI is superior to the AFA. The BGI coefficients need to be determined only once, given the radiometer configuration, and the inversion procedure reduces to a weighted sum of the measurements Equation (2). The Fourier transform and inverse Fourier transform need to be applied repeatedly in the AFA when processing multiple satellite images.

3. Results

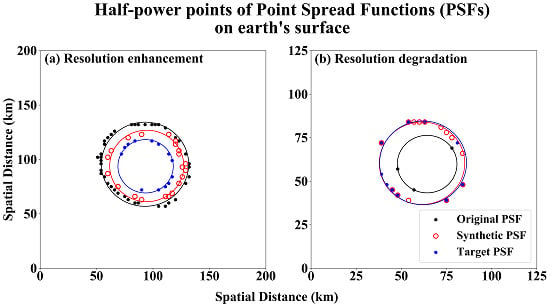
3.1. Reconstructed PSF by the BGI

Following the procedure described in Section 2.2, BGI coefficients are generated for the ATMS onboard the NOAA-20 satellite. As shown in the objective function, i.e., Equation (4b), the reconstructed PSF can be expressed as the sum of the integration of the original PSF weighted by its corresponding coefficient over the overlap between the original and target FOVs. For the AFA, in which the antenna patterns are not projected onto the earth’s surface, reconstructed PSFs are not available.

To illustrate the BGI’s remapping capability, reconstructed PSFs are computed for resolution enhancement and degradation and compared with the original and target PSFs. Figure 2 shows the resolution enhancement from ATMS channel 1 to an AMSU-A-like channel. The top three panels are the original, synthetic, and target PSFs. To clarify the comparison, all PSFs are displayed within the 2.5 times beam width of the target FOV. The comparison shows that the reconstructed PSF is narrower than the original PSF and closer to the target PSF. Fast Fourier transforms convert these PSFs to the frequency domain (Figure 2d–f). The BGI enhances high-frequency components of the PSF to some extent. Figure 3 shows the resolution degradation from ATMS channel 3 to an AMSU-A-like channel. The BGI suppresses the high-frequency components in the PSF (Figure 3d–f) and makes the synthetic PSF match the target one well (Figure 3a–c).

Based on the original, synthetic, and target PSFs in the space domain, the beam widths of the response functions before and after correction can be estimated. To do so, the half-power points of the PSFs at nadir, i.e., the points with a value of 0.5 in Figure 2a–c and Figure 3a–c, are extracted. These points are then fitted with a circle formula (Figure 4). From the diameter of the circle and the altitude of the satellite (824 km for NOAA-20), the beam widths can be estimated (

Table 1. The beam widths of the response functions before and after correction.

	Beam Width (deg)
	Original	Synthetic	Target
Enhancement	5.4	4.6	3.4
Degradation	2.3	3.3	3.3

). Results show that the enhancement procedure narrows the beam width by 15%. The correction for resolution degradation is almost perfect, as expected.

The comparison between the PSFs before and after applying the BGI correction demonstrates that the BGI can achieve some improvement for the resolution enhancement and can near-perfectly match the PSFs for the resolution degradation. This can be explained by the noise penalty term in the objective function of Equation (4a). The resolution enhancement is essentially a procedure to amplify the high-frequency components in a signal. It is inevitable that the noise of the signal is amplified as well. The resolution has to be sacrificed to some extent to avoid introducing any drastic increases in the instrument noise. The compromise between resolution and noise is made through minimizing Equation (4a) with a properly selected tradeoff factor $\gamma$. That is why the BGI cannot perfectly match the PSFs and why the resolution enhancement it can achieve is limited. On the contrary, for resolution degradation, the high-frequency components in the signal are suppressed, as is the noise. The noise penalty term in Equation (4a) is no longer needed. Therefore, the BGI can near-perfectly match the synthetic PSF to the target one. Note that the AFA also has its own strategy to suppress the noise, i.e., adding a low-pass filter to the manipulating term in Equation (7). This may explain the phenomena observed in the simulations in the following section.

3.2. Simulation Comparison between the BGI and the AFA

While the BGI and AFA have a long-term application in ATMS data pre-processing, and the remapped datasets are widely used by the scientific community, their strengths and weaknesses have never been compared. Direct validation of the remapped fields using real ATMS data is nearly impossible because the responses of the different channels to a given scene are different. However, simulated data are an excellent substitute [12,16].

In this study, Ta observed with a certain antenna pattern are simulated by the Community Radiative Transfer Model (CRTM) for the atmosphere and surface geophysical parameters provided by the Global Forecast System (GFS) with a 0.12° grid resolution. The specific procedure is as follows. Through a geolocation model incorporating the ATMS instrument scan geometry, the PSF at each FOV is generated by projecting the real antenna pattern onto the earth’s surface. The PSF within the main beam width is divided into sub-beam intervals at a 3-km resolution. Then the scene Tb at each projected point is calculated from the GFS geophysical parameters using the CRTM. Equation (1) derives Ta from the convolution of Tb with the PSF. Finally, Gaussian white noise is added to the NEDT of each channel (0.22 K and 0.32 K for ATMS channels 1 and 3, respectively).

3.2.1. Evaluation of Remapping Capabilities

NOAA-20 ATMS observations with original and target antenna patterns were simulated for Hurricane Dorian at 18:00 UTC 31 August 2019 to investigate the remapping capabilities of these algorithms. ATMS data used in this study are obtained from the NOAA Comprehensively Large Array-data Stewardship System website: https://www.bou.class.noaa.gov/saa/products/welcome;jsessionid=429B2AC656CF5F31AF12161E3B819B39. Channel noise is added to the simulation of the original observations. The BGI and AFA are then applied to the original measurements to generate the remapped results. The remapped and target data are compared to make a quantitative evaluation of the remapping algorithms.

Figure 5 presents the simulation results for ATMS channel 1. Figure 5a–b are the ATMS channel-1 datasets simulated with 5.2° and 3.3° beam widths. These two datasets are regarded as the raw observations and the simulated truth, respectively. Figure 5c–d are the observations with the expected 3.3° beam width remapped by the BGI and the AFA. Figure 5e–f presents the bias between the remapped data and the simulated truth. Both algorithms provide better definitions of the hurricane center and the islands than the non-enhanced image. However, both produce large biases around coastlines. Specifically, negative biases appear over land and positive biases over water, indicating that the resolution enhancement for the sharp change in signal is insufficient. This is due to the fact that the beam width of the synthetic PSF is larger than that of the expected one, which is consistent with Figure 4a and Table 1. The remapped PSF therefore has higher gain from the ocean (lower Tbs) than expected when the beam center is over land and higher gain from land (higher Tbs) when the beam center is over water. As discussed in Section 3.1, the resolution enhancement has to be sacrificed to suppress the amplification of noise and that leads to the imperfect matching of the PSFs and consequently the insufficient enhancement for the sharp change in signal. However, the issue of the insufficient enhancement appears less serious in the BGI image than in the AFA image (see the west coastline of south Florida). But the noise in the BGI image is larger than that in the AFA image. This indicates that the BGI places more emphasis on resolution matching and less on noise suppression than the AFA.

The most distinct difference between the AFA and BGI remapping error images (Figure 5e–f) is a noticeable bias, as high as 2.5 K, found towards the ends of the scan lines in the AFA image. The AFA image also shows a larger bias around the hurricane center than shown in the BGI image. Focusing on the north coastline of Cuba, the bias from the AFA increases with scan angle, a pattern not obvious in the BGI bias image. This demonstrates that the remapping accuracy of the AFA deteriorates as the scan angle increases. The BGI does not have this issue. That the AFA transformation uses the antenna pattern instead of the PSF and that the geometric deformation of the along-scan FOVs is neglected may explain this. Section 4 discusses this further.

Figure 6 presents the simulation results for ATMS channel 3. The BGI image approximates the simulated truth well, consistent with the fact that the reconstructed PSF for resolution degradation perfectly matches the target one (Figure 3). The AFA image still has some bias around the coastlines, with positive biases over land and negative biases over water, showing that the smoothness over the sharp signal change is insufficient. The use of antenna gain instead of the PSF in the AFA may explain this. Both algorithms reduce the observation noise significantly. This is because the degradation process reduces the resolution and the noise of these channels substantially.

The bias and standard deviation of the error for both original and remapped observations at different FOV positions are calculated to investigate the performance of the algorithms along the scan lines (Figure 7). The most significant reduction in the bias and standard error occurs at FOVs that contain coastlines. For the hurricane center over the ocean observed around nadir, the bias and standard error reduce after remapping. From FOVs 60–70, where no sharp change in Ta appears, the resolution enhancement amplifies the standard error, and the resolution degradation alleviates the standard error, illustrating the noise changes caused by the remapping process. The bias at the scan end of channel 1 caused by the AFA is clearly seen, compared to the observations at other FOVs over the ocean.

PSF mismatch and the noise variation are both responsible for the remapping errors observed in Figure 5 and Figure 6. To quantitatively evaluate the noise change arising from the remapping algorithms and its contribution to the total error, the original channel NEDT, the noise component, and the root-mean-square error (RMSE) of the raw and remapped data relative to the simulated truth were calculated (

Table 2. Root-mean-square errors (RMSEs) and noise components for the raw and remapped observations relative to the simulated truth.

Channel	NEDT	Algorithm	RMSE (K)	Noise Component (K)
1	0.22	none	2.61	—
		BGI	1.59	0.69
		AFA	1.54	0.24
3	0.32	none	1.14	—
		BGI	0.13	0.09
		AFA	0.20	0.11

). For the BGI, the noise component after remapping was derived from the original NEDT and the BGI coefficients through Equation (4c). For the AFA, without such an explicit expression, the standard error of FOVs 60–70 was regarded as the noise component. This assumption is reasonable because Tbs are distributed evenly within these FOVs, so the standard error is contributed by noise rather than a PSF mismatch.

The numbers in Table 2 show that both algorithms reduce the RMSE dramatically after remapping. Specifically, for resolution enhancement, both methods reduce the RMSE to a similar level, i.e., ~60% of the RMSE of the non-enhanced image. The BGI amplifies the noise component by 0.5 K, while the AFA maintains it at its original level. Given that the RMSE is the total contribution of the PSF mismatch and the noise component, this indicates that the BGI does a better PSF matching than the AFA. For resolution degradation, the BGI and the AFA reduce the RMSE to 11% and 16% of the original level, respectively. Both algorithms reduce the noise component by 0.2 K. This also indicates that the BGI matches PSFs better than the AFA.

3.2.2. The Impact of Antenna Pattern Irregularity

Apart from the way of incorporating the antenna gain function, the BGI and the AFA also differ in the choice of the antenna pattern. In the AFA, a Gaussian function approximates the ATMS antenna pattern while in the BGI, adopted is the real one measured during the prelaunch test. For a comparison with the PSFs projected from the real antenna pattern (Figure 2a and Figure 3a), Figure 8 shows the PSFs of the Gaussian-shaped antenna pattern. The irregularities of the real antenna patterns are clear. Note that real antenna patterns generate the Ta fields in the experiments, making the simulations more accurate. This section discusses the impact of the irregularity of the antenna pattern on remapping.

Chosen to carry out this sensitivity study is the BGI algorithm because of its flexibility in switching the antenna pattern. A new set of BGI coefficients generated with the Gaussian-shaped antenna pattern used in the AFA is applied to the raw observations. Figure 9 shows the difference between the remapped data and the simulated truth. Compared with Figure 5e and Figure 6e, approximating the ATMS antenna pattern by a Gaussian function leads to some bias around the hurricane center and coastlines. The RMSE of the enhanced and degraded images increases to 1.65 K and 0.15 K, respectively. As mentioned in Section 2, the remapping algorithms are highly dependent on the overlaps among the raw PSFs and the expected ones. Therefore, the accuracy of the PSF has a direct impact on the accuracy of remapping results. Using a Gaussian function to approximate the real antenna pattern leads to errors in remapping the coefficients and, consequently, to errors in the reconstructed images.

In summary, both the BGI and the AFA are capable of enhancing and degrading the resolution of data. The BGI matches the antenna pattern more accurately than the AFA, especially for resolution degradation. It produces less bias around coastlines, the hurricane center, and scan ends than the AFA. However, the BGI improves the resolution at the expense of increasing the noise level by 0.5 K, while the AFA manages to keep the noise at its original level. Both algorithms are able to reduce the noise level to a large extent in resolution degradation. Approximating the antenna pattern with a Gaussian function could lead to some bias in the remapped results.

3.3. Assessing the BGI and the AFA Using Actual Data

Having examined simulated images, we now consider actual data in a qualitative assessment of algorithm performance. Remapping the real measurements is similar to remapping the simulated dataset. Figure 10 shows the raw observations and remapping results of NOAA-20 ATMS channels 1 and 3 for Hurricane Dorian at 18:00 UTC 31 August 2019. As predicted by the simulation results, details of the hurricane center structure and the islands stand out more clearly in the enhanced images (Figure 10a,c,e), becoming obscure in the degraded images (Figure 10b,d,f). Although not explicitly shown in the figure, the AFA-enhanced image has a 1.5 K positive deviation from the BGI image at the edges of the scan lines. In the enhancement case, the BGI noticeably amplifies the instrument noise, well maintained by the AFA. In the degradation case, both algorithms manage to reduce the noise. These findings are consistent with the conclusions drawn from the simulations in the previous section.

The white lines in Figure 10a,b show a cross-section of Ta selected to show the impact of remapping around coastlines. Figure 11 shows a plot of the observations before and after the remapping process for channels 1 and 3. FOVs 5–10 are over the Gulf of Mexico, FOVs 20–25 are over the Atlantic Ocean, and FOV 15 is over Lake Okeechobee. For channel 1, after enhancement, more sharply delineated are the Atlantic and Gulf coasts, shown by an increase in the gradient across the coastlines. For channel 3, after degradation, decreased is the gradient across the coastlines, and smoothed out is Lake Okeechobee. For both cases, the BGI seems to have a slightly stronger effect in remapping than the AFA. This is expected because the simulations in Section 3.2 show that the BGI has a higher remapping accuracy than the AFA, and the issues of insufficiency in resolution enhancement and degradation around coastlines are less serious in the BGI than in the AFA.

4. Discussion

The application of the two remapping algorithms to the simulated and actual ATMS datasets shows that the remapping accuracy of the BGI is higher than that of the AFA. Compared to the BGI, the AFA-enhanced image has a larger bias around coastlines and the hurricane center where sharp changes in the signal occur. The remapping accuracy of the AFA deteriorates as the scan angle increases, producing more than a 1.5 K positive bias towards the scan ends. As for the degraded image, the bias around coastlines still exists in the AFA image but not in the BGI image. An explanation of the persistence of this bias found in AFA remapped images is that the AFA performs the remapping with the antenna pattern in the antenna-viewing coordinate system instead of projected onto the earth’s surface and neglects the geometric deformation of the along-scan FOVs. Equation (1) shows that remapping algorithms should be carried out in the image domain, the same domain in which the observations lie in. Therefore, what is needed is the transformation of the antenna pattern to a PSF before application in the remapping process. Figure 1 shows that the relative geometry of the along-scan FOV changes dramatically due to the ATMS scan mode and the curvature of the earth’s surface. Since remapping algorithms highly depend on the overlap among FOVs, space-variant PSFs should be used in the algorithms. The BGI incorporates these factors into its process by projecting the antenna pattern onto the earth’s surface and producing coefficients for each FOV position. This strategy makes its remapping more accurate than the AFA remapping.

Some filter-based deconvolution algorithms similar to the AFA have already incorporated the along-scan deformation of FOVs using space-variant PSFs [17,30,31,32]. In these algorithms, filtering is completed along each column of the image with a PSF at that specific scan position, since the relative geometry changes of the data in the along-track direction almost stay the same. The scan is usually divided into a few regions, and the filtering is carried out in each region with the same PSF to reduce the computation time. We believe that the remapping accuracy of the AFA can be improved by following the steps of these deconvolution algorithms. To avoid the bias caused by the irregularity of the antenna pattern, the real antenna pattern measured in the prelaunch ground test, instead of an approximation to a Gaussian function, should also be utilized in the remapping algorithms.

5. Conclusions

The applications of spaceborne, microwave radiometer data in atmospheric remote sensing are often hampered by the nonuniform spatial resolutions available from various sensors and at different frequencies. Much effort has been made to develop remapping algorithms unifying the resolutions to address this problem. In this paper, presented was a comparison of two typical methods, the Backus–Gilbert inversion (BGI) and a filter algorithm (AFA), remapping in spatial and frequency domains, respectively. They both have long been applied in Advanced Technology Microwave Sounder (ATMS) operational data preprocessing. An investigation of their strengths and weaknesses is thus necessary.

In this study, compared were the BGI and AFA algorithms via simulations and actual ATMS data. Both algorithms can produce Advanced Microwave Sounding Unit-A (AMSU-A)-like ATMS observations. The BGI matches the antenna pattern more accurately than the AFA. Specifically, for resolution enhancement, i.e., remapping ATMS channel-1 data with a 5.2° field-of-view (FOV) to an AMSU-A-like 3.3° FOV, both algorithms are capable of enhancing the resolution to some extent. The BGI produces less bias than the AFA around coastlines and hurricane centers where the antenna temperature changes sharply. In addition, the AFA has a noticeable bias towards the ends of scan lines. However, the BGI achieves the resolution enhancement at the expense of increasing the noise level by 0.5 K, while the AFA maintains the noise at its original level. For resolution degradation, i.e., remapping ATMS channel-3 observations with a 2.2° FOV to an AMSU-A-like 3.3° FOV, the BGI shows no obvious bias, while the AFA still has some bias around coastlines. Both algorithms suppress the noise level by 0.2 K.

The use of the antenna pattern instead of a point spread function in the AFA algorithm causes the persistent bias found in the AFA-remapped image. This not only leads to an inaccurate antenna temperature expression but also leads to the neglect of the geometric deformation of the along-scan FOVs. Neglecting the relative geometry change will make the calculation of the overlaps among FOVs inaccurate, which has an important effect on the remapping algorithms. Approximating the antenna pattern with a Gaussian function also contributes toward some bias in the remapped results. Therefore, to improve the remapping accuracy of the AFA, recommended is using the real antenna pattern and its projection onto the earth’s surface in the remapping procedure. The amplification of noise in resolution enhancement by the BGI, which outperforms the AFA by producing less bias around areas of large signal changes, is inevitable. A possible solution might be passing the enhanced image through a carefully designed low-pass filter. Further fine-tuning of the parameters in both algorithms to adapt them to specific Earth surface characteristics and FOV positions may also help improve their remapping qualities. Our future work will explore these topics to further improve the ATMS remapping accuracy.