Simulated Data to Estimate Real Sensor Events—A Poisson-Regression-Based Modelling
Abstract
:1. Introduction
2. Review of Simulation Tools for Smart Environments
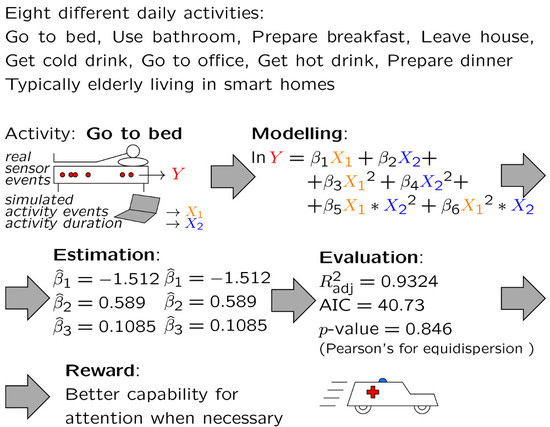
3. Method
3.1. Overdispersion
3.2. Normally Distributed Residuals
3.3. Independence
4. Experiment Description
Initial instructions
- Please close each door after passing through.
- Please turn off each domestic appliance after use.
- You will be guided through each activity in sequence, please remember to select the “Stop/Start” button after each activity is complete.
- Time is not an issue in this experiment. Do not worry about needing to take time to re-read an activity description.
Activity 1: Go to bed
Activity 2: Use bathroom
Activity 3: Prepare breakfast
Activity 4: Leave house
Activity 5: Get cold drink
Activity 6: Go to Office
Activity 7: Get hot drink
Activity 8: Prepare dinner
5. Results and Discussion
5.1. Contrast between Simulated and Real Sensor Events
5.1.1. Door Sensors: Bedroom Door (ADL: Go to bed)
5.1.2. Pressure Sensors: Chair Pressure (ADL: Prepare Breakfast)
5.2. Predicting Real SEPA Using Simulated Data: The Application of Poisson Regression
5.2.1. Sensor-Based Poisson Regression Model
Sensor 1: Bedroom Door (ADL: Go to Bed)
Sensor 2: Bed Pressure (ADL: Go to Bed)
Sensor 3: Bathroom Door (Use Bathroom)
Sensor 4: Refrigerator (Prepare Breakfast)
Sensor 5: Chair Pressure (Prepare Breakfast)
Sensor 6: Chair Pressure (Prepare Dinner)
5.2.2. Poisson Regression Incorporating Dummy Variables
- = 0, = 0
- = 0, = 1
- = 1, = 0
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Anderson-Darling |
| ADL | Activities of Daily Living |
| CI | Confidence interval |
| GP | Generalized Poisson |
| HINT | Halmstad Intelligent Home |
| IE Sim | Intelligent Environmental Simulation |
| IoT | Internet of Things |
| PIR | Passive Infrared |
| Quantile-Quantile | |
| RFID | Radio Frequency Identification |
| SD | Statistically different |
| SE | Statistically equivalent |
| SEPA | Sensor events per activity |
References
- Ortiz, M.A.; López-Meza, P. Using computer simulation to improve patient flow at an outpatient internal medicine department. In Proceedings of the International Conference on Ubiquitous Computing and Ambient Intelligence, Las Palmas de Gran Canaria, Spain, 29 November–2 December 2016; Springer: Cham, Switzerland, 2016; pp. 294–299. [Google Scholar]
- Barrios, M.A.O.; Caballero, J.E.; Sánchez, F.S. A methodology for the creation of integrated service networks in outpatient internal medicine. In Ambient Intelligence for Health; Springer: Cham, Switzerland, 2015; pp. 247–257. [Google Scholar]
- Cheng, L.; Nugent, C.D. Human Activity Recognition and Behaviour Analysis, 1st ed.; Chapter Sensor-Based Activity Recognition Review; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Ortiz-Barrios, M.A.; Herrera-Fontalvo, Z.; Rúa-Muñoz, J.; Ojeda-Gutiérrez, S.; De Felice, F.; Petrillo, A. An integrated approach to evaluate the risk of adverse events in hospital sector: From theory to practice. Manag. Decis. 2018, 56, 2187–2224. [Google Scholar] [CrossRef] [Green Version]
- Rafferty, J.; Nugent, C.D.; Liu, J.; Chen, L. From activity recognition to intention recognition for assisted living within smart homes. IEEE Trans. Hum.-Mach. Syst. 2017, 47, 368–379. [Google Scholar] [CrossRef] [Green Version]
- Nugent, C.; Synnott, J.; Gabrielli, C.; Zhang, S.; Espinilla, M.; Calzada, A.; Lundstrom, J.; Cleland, I.; Synnes, K.; Hallberg, J.; et al. Improving the quality of user generated data sets for activity recognition. In Ubiquitous Computing and Ambient Intelligence; Springer: Cham, Switzerland, 2016; pp. 104–110. [Google Scholar]
- Helal, S.; Kim, E.; Hossain, S. Scalable approaches to activity recognition research. In Proceedings of the 8th International Conference Pervasive Workshop, Helsinki, Finland, 17–20 May 2010; pp. 450–453. [Google Scholar]
- Barrios, M.O.; Jiménez, H.F.; Isaza, S.N. Comparative analysis between ANP and ANP-DEMATEL for six sigma project selection process in a healthcare provider. In International Workshop on Ambient Assisted Living; Springer: Cham, Switzerland, 2014; pp. 413–416. [Google Scholar]
- Barrios, M.O.; Jiménez, H.F. Reduction of average lead time in outpatient service of obstetrics through six sigma methodology. In Ambient Intelligence for Health; Springer: Cham, Switzerland, 2015; pp. 293–302. [Google Scholar]
- Tapia, E.M.; Intille, S.S.; Larson, K. Activity recognition in the home using simple and ubiquitous sensors. In Proceedings of the International Conference on Pervasive Computing, Vienna, Austria, 21–23 April 2004; Springer: Cham, Switzerland, 2004; pp. 158–175. [Google Scholar]
- Cook, D.; Schmitter-Edgecombe, M.; Crandall, A.; Sanders, C.; Thomas, B. Collecting and disseminating smart home sensor data in the CASAS project. In Proceedings of the CHI Workshop on Developing Shared Home Behavior Datasets to Advance HCI and Ubiquitous Computing Research, Boston, MA, USA, 4–9 April 2009; pp. 1–7. [Google Scholar]
- Van Kasteren, T.; Noulas, A.; Englebienne, G.; Kröse, B. Accurate activity recognition in a home setting. In Proceedings of the 10th international conference on Ubiquitous computing, Seoul, Korea, 21–24 September 2008; pp. 1–9. [Google Scholar]
- Alshammari, N.; Alshammari, T.; Sedky, M.; Champion, J.; Bauer, C. Openshs: Open smart home simulator. Sensors 2017, 17, 1003. [Google Scholar] [CrossRef] [Green Version]
- De-La-Hoz-Franco, E.; Ariza-Colpas, P.; Quero, J.M.; Espinilla, M. Sensor-based datasets for human activity recognition–A systematic review of literature. IEEE Access 2018, 6, 59192–59210. [Google Scholar] [CrossRef]
- Rafferty, J.; Synnott, J.; Nugent, C.D.; Ennis, A.; Catherwood, P.A.; McChesney, I.; Cleland, I.; McClean, S. A Scalable, Research Oriented, Generic, Sensor Data Platform. IEEE Access 2018, 6, 45473–45484. [Google Scholar] [CrossRef]
- Synnott, J.; Nugent, C.; Jeffers, P. Simulation of smart home activity datasets. Sensors 2015, 15, 14162–14179. [Google Scholar] [CrossRef] [PubMed]
- Lundström, J.; Synnott, J.; Järpe, E.; Nugent, C.D. Smart home simulation using avatar control and probabilistic sampling. In Proceedings of the 2015 IEEE International Conference On Pervasive Computing And Communication Workshops (Percom Workshops), St. Louis, MO, USA, 23–27 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 336–341. [Google Scholar]
- Ortiz-Barrios, M.; Lundström, J.; Synnott, J.; Järpe, E.; Sant’Anna, A. Complementing real datasets with simulated data: A regression-based approach. In Multimedia Tools and Applications; Springer: Cham, Switzerland; pp. 1–24.
- Schreiber, T.; Schmitz, A. Surrogate time series. Phys. D Nonlinear Phenom. 2000, 142, 346–382. [Google Scholar] [CrossRef] [Green Version]
- Maiwald, T.; Mammen, E.; Nandi, S.; Timmer, J. Surrogate data—A qualitative and quantitative analysis. In Mathematical Methods in Signal Processing and Digital Image Analysis; Springer: Cham, Switzerland, 2008; pp. 41–74. [Google Scholar]
- Salazar, A.; Safont, G.; Vergara, L. Surrogate techniques for testing fraud detection algorithms in credit card operations. In Proceedings of the 2014 International Carnahan Conference on Security Technology (ICCST), Rome, Italy, 13–16 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Abroug, F.; Ouanes-Besbes, L.; Elatrous, S.; Brochard, L. The effect of prone positioning in acute respiratory distress syndrome or acute lung injury: A meta-analysis. Areas of uncertainty and recommendations for research. Intensive Care Med. 2008, 34, 1002. [Google Scholar] [CrossRef]
- Synnott, J.; Chen, L.; Nugent, C.D.; Moore, G. The creation of simulated activity datasets using a graphical intelligent environment simulation tool. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4143–4146. [Google Scholar]
- Ariani, A.; Redmond, S.J.; Chang, D.; Lovell, N.H. Simulation of a smart home environment. In Proceedings of the 2013 3rd International Conference on Instrumentation, Communications, Information Technology and Biomedical Engineering (ICICI-BME), Bandung, Indonesia, 7–8 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 27–32. [Google Scholar]
- Francillette, Y.; Boucher, E.; Bouzouane, A.; Gaboury, S. The Virtual Environment for Rapid Prototyping of the Intelligent Environment. Sensors 2017, 17, 2562. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, B.; Min, H.; Bang, G.; Ko, I. The User Activity Reasoning Model in a Virtual Living Space Simulator. Int. J. Softw. Eng. Its Appl. 2015, 9, 53–62. [Google Scholar] [CrossRef]
- Lee, J.W.; Cho, S.; Liu, S.; Cho, K.; Helal, S. Persim 3d: Context-driven simulation and modeling of human activities in smart spaces. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1243–1256. [Google Scholar] [CrossRef]
- McGlinn, K.; O’Neill, E.; Gibney, A.; O’Sullivan, D.; Lewis, D. SimCon: A Tool to Support Rapid Evaluation of Smart Building Application Design using Context Simulation and Virtual Reality. J. UCS 2010, 16, 1992–2018. [Google Scholar]
- Renoux, J.; Klugl, F. Simulating daily activities in a smart home for data generation. In Proceedings of the 2018 Winter Simulation Conference (WSC), Göteborg, Sweden, 9–12 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 798–809. [Google Scholar]
- Mendez-Vazquez, A.; Helal, A.; Cook, D. Simulating events to generate synthetic data for pervasive spaces. In Workshop on Developing Shared Home Behavior Datasets to Advance HCI and Ubiquitous Computing Research; 2009; Available online: https://pdfs.semanticscholar.org/a7ce/e34ebf272ba18eb60f1a23bd713890890e0c.pdf (accessed on 19 February 2020).
- Cameron, A. Regression Analysis of Count Data; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Kunkler, M. Modelling negatives in stochastic reserving models. Insur. Math. Econ. 2006, 38, 540–555. [Google Scholar] [CrossRef]
- Andersson, P.K.; Skovgaard, L.T. Regression with Linear Predictors; Springer: Cham, Switzerland, 2010. [Google Scholar] [CrossRef]
- Joe, H.; Zhu, R. Generalized Poisson distribution: The property of mixture of Poisson and comparison with negative binomial distribution. Biom. J. 2005, 47, 219–229. [Google Scholar] [CrossRef] [PubMed]
- Consul, P.; Famoye, F. Generalized Poisson regression-model. Commun. Stat. Theory Methods 1992, 21, 89–109. [Google Scholar] [CrossRef]
- Marsaglia, G. Evaluating the Anderson-Darling Distribution. J. Stat. Softw. 2005, 9, 219–229. [Google Scholar] [CrossRef] [Green Version]
- Ljung, G.; Box, G. On a Measure of a Lack of Fit in Time Series Models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Lundström, J.; De Morais, W.O.; Menezes, M.; Gabrielli, C.; Bentes, J.; Sant’Anna, A.; Synnott, J.; Nugent, C. Halmstad intelligent home-capabilities and opportunities. In Proceedings of the International Conference on IoT Technologies for HealthCare, Västerås, Sweden, 18–19 October 2016; Springer: Cham, Switzerland, 2016; pp. 9–15. [Google Scholar]
- Nisbet, R.; Elder, J.; Miner, G. Handbook of Statistical Analysis and Data Mining Applications; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Torrey, L.; Shavlik, J. Transfer learning. Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods, and Techniques; IGI Global: Hershey, PA, USA, 2009. [Google Scholar] [CrossRef] [Green Version]






| Author | Date | 2D/3D | Comparison with Real Data |
|---|---|---|---|
| OpenSHS [13] | 2017 | 3D | No |
| Park [26] | 2015 | 3D | No |
| PerSim [27] | 2015 | 3D | Yes |
| IE Sim [23] | 2015 | 3D | Yes |
| Ariani [24] | 2013 | 2D | No |
| SimCon [28] | 2010 | 3D | No |
| Variable | Mean | Standard dev. | S.E. of the Mean |
|---|---|---|---|
| SEPA_Bedroom door_Simulation | 1.750 | 1.165 | 0.412 |
| SEPA_Bedroom door_Real world | 4.125 | 1.126 | 0.398 |
| Difference | 1.685 | 0.596 |
| Sensor–Activity | Two-Sided CI for the Mean Difference between Real and Simulated SEPA (95%) | t-Statistic | p-Value | Finding |
|---|---|---|---|---|
| Bedroom door–Go to bed | 0.005 | SD | ||
| Bathroom door–Use bathroom | 0.026 | SD | ||
| Bowl cupboard–Prepare breakfast | 0 | 1.0 | SE | |
| Refrigerator–Prepare breakfast | 0.020 | SD | ||
| Refrigerator–Get cold drink | 0.0448 | SD | ||
| Bowl cupboard–Prepare dinner | 0.000 | SD |
| Variable | Mean | Standard dev. | Standard Error of the Mean |
|---|---|---|---|
| SEPA_Chair pressure_Synthetic | 4.875 | 1.885 | 0.666 |
| SEPA_Chair pressure_Real world | 1.250 | 1.282 | 0.453 |
| Difference | 2.446 | 0.865 |
| Sensor–Activity | Two-Sided CI for the Difference between Real and Simulated SEPA | t-Value | p-Value | Conclusion |
|---|---|---|---|---|
| Bed pressure–Go to bed | (90%) | 0.065 | SD | |
| Chair pressure–Prepare breakfast | (95%) | 0.004 | SD | |
| Chair pressure–Leave house | (95%) | 0.103 | SE | |
| Office chair pressure 3–Be in the office | (95%) | 0.403 | SE | |
| Chair pressure–Prepare dinner | (95%) | 0.000 | SD |
| Sensor | Bedroom door | Bed pressure | Bedroom door | Refrigerator | Chair pressure | Chair pressure |
|---|---|---|---|---|---|---|
| ADL | Go to bed | Go to bed | Use bathroom | Prepare breakfast | Prepare breakfast | Prepare dinner |
| (adj.) | 0.9021 | 0.9324 | 0.9509 | 0.9292 | 0.5636 | 0.7311 |
| AIC | 35.57 | 40.73 | 30.59 | 29.98 | 19.44 | 11.69 |
| Assessment of Poisson regression model | ||||||
| Auto-correlation T-statistic | 0.44 | 0.61 | 1.0 | 0.82 | 1.45 | 1.14 |
| Normally distributed residuals p-value | 0.338 | 0.688 | 0.987 | 0.566 | 0.508 | 0.846 |
| Equidispersion Deviance p-value | 0.829 | 0.721 | 0.987 | 0.965 | 0.816 | 0.946 |
| Equidispersion Pearson p-value | 0.846 | 0.716 | 0.988 | 0.965 | 0.816 | 0.960 |
| Predictor | DF | Contribution | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| 1 | 29.81 | 29.812 | 128.25 | 0.000 | |
| 1 | 3.29 | 3.296 | 14.18 | 0.001 | |
| 1 | 6.13 | 6.132 | 26.38 | 0.000 | |
| 1 | 17.71 | 17.716 | 76.22 | 0.000 | |
| 1 | 4.40 | 4.405 | 18.95 | 0.000 | |
| 1 | 1.43 | 1.428 | 6.15 | 0.018 | |
| 1 | 2.89 | 2.892 | 12.44 | 0.001 | |
| Error | 35 | 8.13 | 0.232 | ||
| Total | 42 | 151 |
| S | (adj.) | (pred) | PRESS | |
|---|---|---|---|---|
| 0.4821 | 0.9461 | 0.9353 | 0.9272 | 10.9856 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortíz-Barrios, M.A.; Cleland, I.; Nugent, C.; Pancardo, P.; Järpe, E.; Synnott, J. Simulated Data to Estimate Real Sensor Events—A Poisson-Regression-Based Modelling. Remote Sens. 2020, 12, 771. https://doi.org/10.3390/rs12050771
Ortíz-Barrios MA, Cleland I, Nugent C, Pancardo P, Järpe E, Synnott J. Simulated Data to Estimate Real Sensor Events—A Poisson-Regression-Based Modelling. Remote Sensing. 2020; 12(5):771. https://doi.org/10.3390/rs12050771
Chicago/Turabian StyleOrtíz-Barrios, Miguel Angel, Ian Cleland, Chris Nugent, Pablo Pancardo, Eric Järpe, and Jonathan Synnott. 2020. "Simulated Data to Estimate Real Sensor Events—A Poisson-Regression-Based Modelling" Remote Sensing 12, no. 5: 771. https://doi.org/10.3390/rs12050771
APA StyleOrtíz-Barrios, M. A., Cleland, I., Nugent, C., Pancardo, P., Järpe, E., & Synnott, J. (2020). Simulated Data to Estimate Real Sensor Events—A Poisson-Regression-Based Modelling. Remote Sensing, 12(5), 771. https://doi.org/10.3390/rs12050771