A Bayesian Three-Cornered Hat (BTCH) Method: Improving the Terrestrial Evapotranspiration Estimation
Abstract
:1. Introduction
2. Study Regions and Datasets
3. Methodology
3.1. Bayesian-Based Three-Cornered Hat (BTCH) Method
3.2. Water Balance Budget Method
3.3. Long-Term Total Water Storage Anomaly Reconstruction
4. Results and Discussions
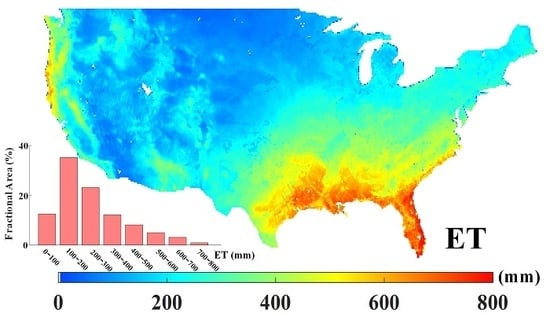
4.1. ET Product from the BTCH Method
4.2. Relationships between BTCH-Integrated ET and Climate Factors
4.3. Interannual Variations of BTCH-Integrated ET Estimates
4.4. Long-Term Reconstruction of GRACE Total Water Storage Anomaly
4.5. Time Window of BTCH Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Scott, R.L.; Huxman, T.E.; Cable, W.L.; Emmerich, W.E. Partitioning of evapotranspiration and its relation to carbon dioxide exchange in a Chihuahuan Desert shrubland. Hydrol. Process. 2006, 20, 3227–3243. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.; Ding, Y.; Wen, Z.; Chen, Y.; Cao, Y.; Ren, J. Spatiotemporal change and trend analysis of potential evapotranspiration over the Loess Plateau of China during 2011–2100. Agric. For. Meteorol. 2017, 233, 183–194. [Google Scholar] [CrossRef] [Green Version]
- Er-Raki, S.; Chehbouni, A.; Boulet, G.; Williams, D.G. Using the dual approach of FAO-56 for partitioning ET into soil and plant components for olive orchards in a semi-arid region. Agric. Water Manag. 2010, 97, 1769–1778. [Google Scholar] [CrossRef] [Green Version]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Ireland, G.; Lamine, S.; Griffiths, H.M.; Ghilain, G.; Anagnostopoulos, V.; North, M.R.; Srivastava, P.K.; Georgopoulou, H. Operational evapotranspiration estimates from SEVIRI in support of sustainable water management. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 175–187. [Google Scholar] [CrossRef] [Green Version]
- Baldocchi, D.; Falge, E.; Gu, L.H.; Olson, R. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Evett, S.R.; Kustas, W.P.; Gowda, P.H.; Anderson, M.C.; Prueger, J.H.; Howell, T.A. Overview of the Bushland Evapotranspiration and Agricultural Remote sensing EXperiment 2008 (BEAREX08): A field experiment evaluating methods for quantifying ET at multiple scales. Adv. Water Resour. 2011, 50, 4–19. [Google Scholar] [CrossRef]
- Liu, S.M.; Li, X.; Xu, Z.W.; Che, T.; Xiao, Q.; Ma, M.M.; Liu, Q.H.; Jin, R.; Guo, J.W.; Wang, L.X.; et al. The Heihe integrated observatory network: A basin-scale land surface processes observatory in China. Vadose Zone J. 2018, 17. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.Q.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.Q.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. 2011, 116, G00J07. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z.; Xia, Y.; Xiao, J.; Zhang, Y.; Ma, Y.; et al. Evaluating different machine learning methods for upscaling evapotranspiration from flux towers to the regional scale. J. Geophys. Res. Atmos. 2018, 123. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E.; Wild, M.; Liang, S. Evidence for decadal variation in global terrestrial evapotranspiration between 1982 and 2002: 1. Model development. J. Geophys. Res. 2010, 115, D20112. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Liang, S. An improved method for estimating global evapotranspiration based on satellite determination of surface net radiation, vegetation index, temperature, and soil moisture. J. Hydrometeorol. 2008, 9, 712–727. [Google Scholar] [CrossRef]
- Zhu, W.; Jia, S.; Lv, A. A universal Ts-VI triangle method for the continuous retrieval of evaporative fraction from MODIS products. J. Geophys. Res. Atmos. 2017, 122. [Google Scholar] [CrossRef]
- Zhao, B.; Mao, K.; Cai, Y.; Shi, J.; Li, Z.; Qin, Z.; Meng, X. A combined Terra and Aqua MODIS land surface temperature and meteorological station data product for China from 2003–2017. Earth Syst. Sci. Data Discuss. 2019. in review. [Google Scholar] [CrossRef] [Green Version]
- Jia, L.; Xi, G.; Liu, S.; Huang, C.; Yan, Y.; Liu, G. Regional estimation of daily to annual regional evapotranspiration with MODIS data in the Yellow River Delta wetland. Hydrol. Earth Syst. Sci. 2009, 13, 1775–1787. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Liu, S.; Song, L.; Xu, Z.; Liu, Y.; Xu, T.; Zhu, Z. Estimation of daily evapotranspiration and irrigation water efciency at a Landsat-like scale for an arid irrigation area using multi-source remote sensing data. Remote Sens. Environ. 2018, 216, 715–734. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Wang, K.; Jia, K.; Chen, J.; Jiang, B.; Fisher, J.B.; Mu, Q.; et al. A satellite-based hybrid algorithm to determine the Priestley-Taylor parameter for global terrestrial latent heat flux estimation across multiple biomes. Remote Sens. Environ. 2015, 165, 216–233. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water. 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Bateni, S.M.; Entekhabi, D.; Jeng, D.S. Variational assimilation of land surface temperature and the estimation of surface energy balance components. J. Hydrol. 2013, 481, 143–156. [Google Scholar] [CrossRef]
- Bateni, S.M.; Entekhabi, D.; Castelli, F. Mapping evaporation and estimation of surface control of evaporation using remotely sensed land surface temperature from a constellation of satellites. Water Resour. Res. 2013, 49, 950–968. [Google Scholar] [CrossRef]
- He, X.L.; Xu, T.R.; Bateni, S.M.; Neale, C.M.U.; Auligne, T.; Liu, S.M.; Wang, K.C.; Mao, K.B.; Yao, Y.J. Evaluation of the Weak Constraint Data Assimilation Approach for Estimating Turbulent Heat Fluxes at Six Sites. Remote Sens. 2018, 10, 1994. [Google Scholar] [CrossRef] [Green Version]
- He, X.L.; Xu, T.R.; Bateni, S.M.; Neale, C.M.U.; Liu, S.M.; Auligne, T.; Wang, K.C.; Zhu, S.D. Mapping Regional Turbulent Heat Fluxes via Assimilation of MODIS Land Surface Temperature Data into an Ensemble Kalman Smoother Framework. Earth Space Sci. 2019, 6. [Google Scholar] [CrossRef] [Green Version]
- He, X.L.; Xu, T.R.; Bateni, S.M.; Ek, M.; Liu, S.M.; Chen, F. Mapping Regional Evapotranspiration in Cloudy Skies via Variational Assimilation of All-Weather Land Surface Temperature Observations. J. Hydrol. 2020. [Google Scholar] [CrossRef]
- Lu, Y.; Steele-Dunne, S.C.; Farhadi, L.; Van de Giesen, N. Mapping surface heat fluxes by assimilating SMAP soil moisture and GOES land surface temperature data. Water Resour. Res. 2017, 53, 10858–10877. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.R.; Bateni, S.M.; Liang, S.; Entekhabi, D.; Mao, K. Estimation of surface turbulent heat fluxes via variational assimilation of sequences of land surface temperatures from Geostationary Operational Environmental Satellites. J. Geophys. Res. 2014, 119, 10–780. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.R.; He, X.L.; Bateni, S.M.; Auligne, T.; Liu, S.M.; Xu, Z.W.; Zhou, J.; Mao, K.B. Mapping Regional Turbulent Heat Fluxes via Variational Assimilation of Land Surface Temperature Data from Polar Orbiting Satellites. Remote Sens. Environ. 2019, 221, 444–461. [Google Scholar] [CrossRef]
- Carrera, M.; Belair, S.; Bilodeau, B. The Canadian Land Data Assimilation System (CaLDAS): Description and synthetic evaluation study. J. Hydrometeor. 2015, 16, 1293–1314. [Google Scholar] [CrossRef]
- Xia, Y.; Hao, Z.; Shi, C.; Li, Y.; Meng, J.; Xu, T.; Wu, X.; Zhang, B. Regional and Global Land Data Assimilation Systems: Innovations, Challenges, and Prospects. J. Meteorol. Res. 2019, 33, 159–189. [Google Scholar] [CrossRef]
- Xu, T.; Liu, S.M.; Liang, S.; Qin, J. Improving predictions of water and heat fluxes by assimilating MODIS land surface temperature products into common land model. J. Hydrometeorol. 2011, 12, 227–244. [Google Scholar] [CrossRef]
- Zhang, B.; Xia, Y.L.; Long, B.; Hobbins, M.; Zhao, X.; Hain, C. Evaluation and comparison of multiple evapotranspiration data models over the contiguous United States: Implications for the next phase of NLDAS (NLDAS-Testbed) development. Agric. For. Meteorol. 2020, 280, 107810. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Wu, B.; Xiong, J.; Yan, N. Etwatch: Models and methods. J. Remote Sens. 2010, 15, 224–230. [Google Scholar]
- Wu, B.; Zhu, W.; Yan, N.; Feng, X.; Xing, Q.; Zhuang, Q. An improved method for deriving daily evapotranspiration estimates from satellite estimates on cloud-free days. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1323–1330. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Hong, Y.; Fisher, J.B.; Zhang, N.; Chen, J.; Cheng, J.; Zhao, S.; Zhang, X.; et al. Bayesian multimodel estimation of global terrestrial latent heat flux from eddy covariance, meteorological, and satellite observations. J. Geophys. Res. Atmos. 2014, 119, 4521–4545. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.; Lievens, H.; Fernández-Prieto, D.; Verhoest, N.E. Improving terrestrial evaporation estimates over continental Australia through assimilation of SMOS soil moisture. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 146–162. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández–Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite–based land evaporation and root–zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, K.E.; Lohmann, D.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Cosgrove, B.A.; Sheffield, J.; Duan, Q.; Luo, L.; et al. The multi–institution North American Land Data Assimilation System (NLDAS): Utilizing multiple GCIP products and partners in a continental distributed hydrological modeling system. J. Geophys. Res. 2004, 109, D07S90. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.R.; Guo, Z.X.; Xia, Y.L.; Ferreira, V.G.; Liu, S.M.; Wang, K.C.; Yao, Y.J.; Zhang, X.J.; Zhao, C.S. Evaluation of twelve evapotranspiration products from machine learning, remote sensing and land surface models over conterminous united states. J. Hydrol. 2019, 578, 124105. [Google Scholar] [CrossRef]
- McCabe, M.F.; Ershadi, A.; Jimenez, C.; Miralles, D.G.; Michel, D.; Wood, E.F. The GEWEX LandFlux project: Evaluation of model evaporation using tower-based and globally gridded forcing data. Geosci. Model Dev. 2016, 9, 283–305. [Google Scholar] [CrossRef] [Green Version]
- Duan, Q.; Phillips, T.J. Bayesian estimation of local signal and noise in multimodel simulations of climate change. J. Geophys. Res. Atmos. 2010, 115, D18123. [Google Scholar] [CrossRef]
- Houghton, J.T.A. Climate Change 2001: The Scientific Basis. In Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2001; p. 892. [Google Scholar]
- Raftery, A.E.; Madigan, D.; Hoeting, J.A. Bayesian model averaging for linear regression models. J. Am. Stat. Assoc. 1997, 92, 179–191. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Zhang, X.; Liang, S.; Yang, H.; Zhou, G. Estimation of clear-sky land surface longwave radiation from MODIS data products by merging multiple models. J. Geophys. Res. Atmos. 2012, 117, D22107. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Gao, X.; Zhao, M.; Guo, Z.; Oki, T.; Hanasaki, N. GSWP-2: Multimodel analysis and implications for our perception of the land surface. Bull. Am. Meteorol. Soc. 2006, 87, 1381–1397. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Liu, S.; Jia, K.; Zhang, X.; Xiao, Z.; Fisher, J.B.; Mu, Q.; et al. Improving global terrestrial evapotranspiration estimation using support vector machine by integrating three process-based algorithms. Agric. For. Meteorol. 2017, 242, 55–74. [Google Scholar] [CrossRef]
- Hobeichi, S.; Abramowitz, G.; Evans, J.; Ukkola, A. Derived Optimal Linear Combination Evapotranspiration (DOLCE): A global gridded synthesis ET estimate. Hydrol. Earth Syst. Sci. 2018, 22, 1317. [Google Scholar] [CrossRef] [Green Version]
- Burba, G.; Anderson, D. A Brief Practical Guide to Eddy Covariance Flux Measurements: Principles and Workflow Examples for Scientific and Industrial Applications; LI-COR Biosciences: Lincoln, NE, USA, 2010. [Google Scholar]
- Scipal, K.; Holmes, T.; De Jeu, R.; Naeimi, V.; Wagner, W. A possible solution for the problem of estimating the error structure of global soil moisture data sets. Geophys. Res. Lett. 2008, 35, L24403. [Google Scholar] [CrossRef] [Green Version]
- Premoli, A.; Tavella, P. A revisited three-cornered hat method for estimating frequency standard instability. IEEE Trans. Instrum. Meas. 1993, 42, 7–13. [Google Scholar] [CrossRef]
- Crow, W.T.; Lei, F.; Hain, C.; Anderson, M.C.; Scott, R.L.; Billesbach, D.; Arkebauer, T. Robust estimates of soil moisture and latent heat flux coupling strength obtained from triple collocation. Geophys. Res. Lett. 2015, 42, 8415–8423. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, V.G.; Montecino, H.D.; Yakubu, C.I.; Heck, B. Uncertainties of the Gravity Recovery and Climate Experiment time–variable gravity-field solutions based on three-cornered hat method. J. Appl. Remote Sens. 2016, 10, 015015. [Google Scholar] [CrossRef]
- Khan, M.S.; Liaqat, U.W.; Baik, J.; Choi, M. Stand–alone uncertainty characterization of GLEAM, GLDAS and MOD16 evapotranspiration products using an extended triple collocation approach. Agric. For. Meteorol. 2018, 252, 256–268. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Crow, W.T.; Anderson, M.C.; Hain, C. An objective methodology for merging satellite- and model-based soil moisture products. Water Resour. Res. 2012, 48, 11502. [Google Scholar] [CrossRef]
- Wu, B.; Xiong, J.; Yan, N.; Yang, L.; Du, X. ETWatch for monitoring regional evapotranspiration with remote sensing. Adv. Rater Sci. 2008, 19, 671–678. [Google Scholar]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational evapotranspiration mapping using remote sensing and weather datasets: A new parameterization for the SSEB approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Crow, W.T.; Cosh, M.H. Estimating spatial sampling errors in coarse–scale soil moisture estimates derived from point–scale observations. J. Hydrometeorol. 2010, 11, 1423–1429. [Google Scholar] [CrossRef]
- Miralles, D.G.; Jimenez, C.; Jung, M.; Michel, D.; Ershadi, A.; McCabe, M.F.; Hirschi, M.; Martens, B.; Dolman, A.J.; Fisher, J.B.; et al. The WACMOS-ET project—Part 2: Evaluation of global terrestrial evaporation data sets. Hydrol. Earth Syst. Sci. 2016, 20, 823–842. [Google Scholar] [CrossRef] [Green Version]
- Burnash, R.J.C.; Ferral, R.L.; McGuire, R.A. A Generalized Stream Flow Simulation System. Conceptual Modeling for Digital Computer; State Department of Water Resources: Sacramento, CA, USA, 1973; Volume 204. [Google Scholar]
- Chen, F.; Janjić, Z.; Mitchell, K. Impact of atmospheric surface-layer parameterizations in the new land-surface scheme of the NCEP mesoscale Eta model. Bound. Layer Meteor. 1997, 85, 391–421. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M. The components of the SVAT scheme and their effects on a GCM’s hydrological cycle. Adv. Water Resour. 1994, 17, 61–78. [Google Scholar] [CrossRef]
- Koster, R.; Suarez, M.; Ducharne, A.; Stieglitz, M.; Kumar, P. A catchment-based approach to modeling land surface processes in a general circulation model 1. Model structure. J. Geophys. Res. Atmos. 2000, 105, 24–809. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14–415. [Google Scholar] [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; et al. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. Atmos. 2012, 17, 1–27. [Google Scholar] [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Cosgrove, B.; Sheffield, J.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; Livneh, B.; et al. Continental-scale water and energy flux analysis and validation for North American Land Data Assimilation System project phase 2 (NLDAS-2): 2. Validation of model-simulated streamflow. J. Geophys. Res. Atmos. 2012, 117, 1–23. [Google Scholar] [CrossRef]
- Xia, Y.; Hobbins, M.T.; Mu, Q.; Ek, M.B. Evaluation of NLDAS-2 evapotranspiration against tower flux site observations. Hydrol. Process. 2015, 29, 1757–1771. [Google Scholar] [CrossRef]
- Xia, Y.; Peter-Lidard, C.D.; Huang, M.; Wei, H.; Ek, M. Improved NLDAS-2 Noah-simulated hydrometeorological products with an interim run. Hydrol. Process. 2015, 29, 780–792. [Google Scholar] [CrossRef]
- Xia, Y.; Cosgrove, B.A.; Mitchell, K.E.; Peters-Lidard, C.D.; Ek, M.B.; Brewer, M.; Mocko, D.; Kumar, S.V.; Wei, H.; Meng, J.; et al. Basin-scale assessment of the land surface water budget in the National Centers for environmental prediction operational and research NLDAS-2 systems. J. Geophys. Res. 2016, 121, 2750–2779. [Google Scholar] [CrossRef] [Green Version]
- Vose, R.S.; Arndt, D.; Banzon, V.F.; Easterling, D.R.; Gleason, B.; Huang, B.; Kearns, E.; Lawrimore, J.H.; Menne, M.J.; Peterson, T.C. NOAA’s merged land–ocean surface temperature analysis. Bull. Am. Meteorol. Soc. 2012, 93, 1677–1685. [Google Scholar] [CrossRef]
- Vose, R.S.; Applequist, S.; Squires, M.; Durre, I.; Menne, M.J.; Williams, C.N., Jr.; Fenimore, C.; Gleason, K.; Arndt, D. Improved historical temperature and precipitation time series for US climate divisions. J. Appl. Meteorol. Climatol. 2014, 53, 1232–1251. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour Res. 2012, 48, 1–11. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Global analysis of approaches for deriving total water storage changes from GRACE satellites. Water Resour. Res. 2015, 51, 2574–2594. [Google Scholar] [CrossRef] [Green Version]
- Jian, X.; Wolock, D.; Lins, H. WaterWatch-Maps, Graphs, and Tables of Current, Recent, and Past Streamflow Conditions; Report; United States Geological Survey: Reston, VA, USA, 2008; pp. 2327–6932. [Google Scholar]
- Xia, Y.; Mocko, D.; Huang, M.; Li, B.; Rodell, M.; Mitchell, K.E.; Cai, X.; Ek, M.B. Comparison and Assessment of Three Advanced Land Surface Models (CLSM–F2.5_NoahMP_CLM4.0) in Simulating Terrestrial Water Storage Components over the United States. J. Hydrometeorol. 2017, 18, 625–649. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Csiszar, I.; Eidenshink, J.; Myneni, R.; Baret, F.; Masuoka, E.; Wolfe, R.E.; Claverie, M. NOAA CDR Program: NOAA Climate Data Record (CDR) of Normalized Difference Vegetation Index (NDVI); Version 4. [indicate subset used]; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2014. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Bondeau, A. Towards global empirical upscaling of FLUXNET eddy covariance observations: Validation of a model tree ensemble approach using a biosphere model. Biogeosciences 2009, 6, 2001–2013. [Google Scholar] [CrossRef] [Green Version]
- Gray, J.E.; Allan, D.W. A method for estimating the frequency stability of an individual oscillator. In Proceedings of the 28th Annual Symposium on Frequency Control, Atlantic City, NJ, USA, 29–31 May 1974; pp. 243–246. [Google Scholar]
- Tavella, P.; Premoli, A. Estimating the instabilities of N clocks by measuring differences of their readings. Metrologia 1994, 30, 479–486. [Google Scholar] [CrossRef]
- Galindo, F.J.; Palacio, J. Post-processing ROA data clocks for optimal stability in the ensemble timescale. Metrologia 2003, 40, S237–S244. [Google Scholar] [CrossRef]
- Galindo, F.J.; Palacio, J. Estimating the instabilities of N correlated clocks. In Proceedings of the 31st Annual Precise Time and Time Interval (PTTI) Meeting, Dana Point, CA, USA, 7–9 December 1999; pp. 285–296. [Google Scholar]
- Torcaso, F.; Ekstrom, C.; Burt, E.; Matsakis, D. Estimating frequency stability and cross-correlations. In Proceedings of the 30th Annual Precise Time and Time Interval Meeting, Reston, VA, USA, 1–3 December 1998. [Google Scholar]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Zeng, N. Seasonal cycle and interannual variability in the Amazon hydrologic cycle. J. Geophys. Res. Atmos. 1999, 104, 9097–9106. [Google Scholar] [CrossRef]
- Mann, H.B. Non-parametric test against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Rahman, M.; Yunsheng, L.; Sultana, N. Analysis and prediction of rainfall trends over Bangladesh using Mann–Kendall, Spearman’s rho tests and ARIMA model. Meteorol. Atmos. Phys. 2017, 129, 409–424. [Google Scholar] [CrossRef]
- Fathian, F.; Dehghan, Z.; Bazrkar, M.H.; Eslamian, S. Trends in hydrological and climatic variables affected by four variations of the Mann-Kendall approach in Urmia Lake basin. Iran. Hydrol. Sci. J. 2016, 61, 892–904. [Google Scholar] [CrossRef] [Green Version]
- Rezaie, H.; Khalili, K.; Khanmohammadi, N.; Nazeri Tahrudi, M. Surface air temperature trends during the last 20 years in Iran. J. Appl. Environ. Biol. Sci. 2014, 4, 40–46. [Google Scholar]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann-Kendall and Spearman’s tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Haan, C.T. Statistical Methods in Hydrology; Iowa State University Press: Ames, IA, USA, 1977. [Google Scholar]
- De la Fuente, A.; Bing, N.; Hoeschele, I.; Mendes, P. Discovery of meaningful associations in genomic data using partial correlation coefficients. Bioinformatics 2004, 20, 3565–3574. [Google Scholar] [CrossRef] [Green Version]
- Thorndike, R.M. Correlational Procedures for Research; Gardner Press Inc.: New York, NY, USA, 1976. [Google Scholar]
- Wilcox, B.P.; Wood, M.K.; Tromble, J.T.; Ward, T.J. A hand-portable single nozzle rainfall simulator designed for use on steep slopes. J. Range Manag. 1986, 39, 375–377. [Google Scholar] [CrossRef]
- Long, D.; Pan, Y.; Zhou, J.; Chen, Y.; Hou, X.Y.; Hong, Y.; Scanlon, B.R.; Longuevergne, L. Global analysis of spatiotemporal variability in merged total water storage changes using multiple GRACE products and global hydrological models. Remote Sens. Environ. 2017, 192, 198–216. [Google Scholar] [CrossRef]
- Henn, B.; Painter, T.H.; Bormann, K.J.; McGurk, B.; Flint, A.L.; Flint, L.E.; White, W.; Lundquist, J.D. High-elevation evapotranspiration estimates during drought: Using streamflow and NASA airborne snow observatory SWE observations to close the upper tuolumne river basin water balance. Water Resour. Res. 2018, 54, 746–766. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A. Trends in evaporation and surface cooling in the Mississippi River basin. Geophys. Res. Lett. 2001, 28, 1219–1222. [Google Scholar] [CrossRef]
- Walter, M.T.; Wilks, D.S.; Parlange, J.-Y.; Schneider, R.L. Increasing evapotranspiration from the conterminous United States. J. Hydrometeorol. 2004, 5, 405–408. [Google Scholar] [CrossRef]
- Bateni, S.M.; Entekhabi, D. Relative efficiency of land surface energy balance components. Water Resour. Res. 2012, 48, W04510. [Google Scholar] [CrossRef]
- Shokri, N.; Lehmann, P.; Vontobel, P.; Or, D. Drying front and water content dynamics during evaporation from sand delineated by neutron radiography. Water Resour. Res. 2008, 44, W06418. [Google Scholar] [CrossRef] [Green Version]
- Shokri, N.; Lehmann, P.; Or, D. Characteristics of evaporation from partially wettable porous media. Water Resour. Res. 2008, 45, W02415. [Google Scholar] [CrossRef] [Green Version]














| ID | Site Name | Period | Location (N°, W°) | Elevation (m) | Land Cover |
|---|---|---|---|---|---|
| US-Bar | Bartlett Experimental Forest | 2004–2005 | 44.06, -71.28 | 272 | DBF |
| US-MOz | Missouri Ozark | 2004–2006 | 38.74, -92.20 | 219 | DBF |
| US-MMS | Morgan Monroe State Forest | 2000–2004 | 39.32, -86.41 | 275 | DBF |
| US-Oho | Ohio Oak Openings | 2004–2005 | 41.55, -83.84 | 230 | DBF |
| US-Blo | Blodgett Forest | 2000–2006 | 38.89, -120.63 | 1315 | ENF |
| US-SP3 | Donaldson | 2000–2004 | 29.75, -82.16 | 50 | ENF |
| US-Fuf | Flagstaff Unmanaged Forest | 2005–2006 | 35.08, -111.76 | 2180 | ENF |
| US-Me2 | Metolius Pine | 2003–2005 | 44.45, -121.55 | 1253 | ENF |
| US-NR1 | Niwot Ridge | 2000–2003 | 40.03, -105.54 | 3050 | ENF |
| US-Wrc | Wind River | 2000–2006 | 45.82, -121.95 | 371 | ENF |
| US-ARM | ARM Southern Great Plains Main | 2003–2006 | 36.60, -97.48 | 314 | Cropland |
| US-Bo1 | Bondville | 2000–2006 | 40.00, -88.29 | 219 | Cropland |
| US-Ne1 | Mead Irrigated | 2001–2005 | 41.16, -96.47 | 361 | Cropland |
| US-Ne2 | Mead Irrigated Rotation | 2002–2005 | 41.16, -96.47 | 362 | Cropland |
| US-Ne3 | Mead Rainfed | 2001–2005 | 41.18, -96.44 | 363 | Cropland |
| Dataset | Data Source | Spatial, Temporal Resolution | Spatial, Temporal Coverage | References |
|---|---|---|---|---|
| P & Ta | NCEI | 4.16 km, monthly | CONUS, 1979–2012 | [74,75] |
| R | USGS | ~2°, daily | CONUS, 1982–2011 | [78] |
| TWSA | GRACE | ~1°, monthly | Global, 2003–2016 | [76] |
| SM & ET | CLM4 | 12.5 km, monthly | CONUS, 1980–2014 | [79] |
| NDVI | AVHRR | 0.05°, daily | Global, 1981–2018 | [80] |
| SE ET | GFET | 50 km, monthly | Global, 1982–2011 | [10,81] |
| RSM ET | GLEAM | 25 km, daily | Global, 1982–2017 | [37] |
| NLDAS-2 ET | Noah28 | 12.5 km, monthly | CONUS, 1979–2013 | [69,70] |
| SAC | ||||
| Mosaic | ||||
| VIC403 | ||||
| NLDAS-testbed ET | CLSM25 | 12.5 km, monthly | CONUS, 1979–2013 | [79] |
| Noah36 | ||||
| NoahMP36 | ||||
| VIC412 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Xu, T.; Xia, Y.; Bateni, S.M.; Guo, Z.; Liu, S.; Mao, K.; Zhang, Y.; Feng, H.; Zhao, J. A Bayesian Three-Cornered Hat (BTCH) Method: Improving the Terrestrial Evapotranspiration Estimation. Remote Sens. 2020, 12, 878. https://doi.org/10.3390/rs12050878
He X, Xu T, Xia Y, Bateni SM, Guo Z, Liu S, Mao K, Zhang Y, Feng H, Zhao J. A Bayesian Three-Cornered Hat (BTCH) Method: Improving the Terrestrial Evapotranspiration Estimation. Remote Sensing. 2020; 12(5):878. https://doi.org/10.3390/rs12050878
Chicago/Turabian StyleHe, Xinlei, Tongren Xu, Youlong Xia, Sayed M. Bateni, Zhixia Guo, Shaomin Liu, Kebiao Mao, Yuan Zhang, Huaize Feng, and Jingxue Zhao. 2020. "A Bayesian Three-Cornered Hat (BTCH) Method: Improving the Terrestrial Evapotranspiration Estimation" Remote Sensing 12, no. 5: 878. https://doi.org/10.3390/rs12050878
APA StyleHe, X., Xu, T., Xia, Y., Bateni, S. M., Guo, Z., Liu, S., Mao, K., Zhang, Y., Feng, H., & Zhao, J. (2020). A Bayesian Three-Cornered Hat (BTCH) Method: Improving the Terrestrial Evapotranspiration Estimation. Remote Sensing, 12(5), 878. https://doi.org/10.3390/rs12050878