Mapping Forest Canopy Fuels in the Western United States with LiDAR–Landsat Covariance
Abstract
:1. Introduction
- (1)
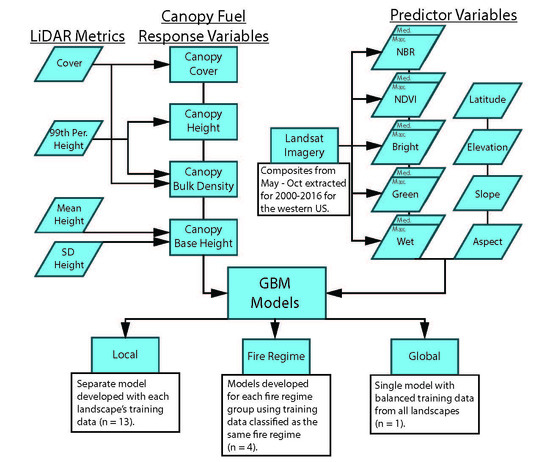
- Create and compare local, biophysically stratified, and global predictive model(s) of canopy fuels variables than can be applied to forested areas in the western US;
- (2)
- Compare model predictions to current LANDFIRE products;
- (3)
- Assess selected model(s) ability to update canopy layers following wildfire disturbance.
2. Materials and Methods
2.1. Data
2.2. LiDAR Processing
2.3. Landsat and LANDFIRE Data Processing
2.4. Dataset Stratification, Sample Weighting, and Model Development
2.5. Spectral Response and Model Performance Assessment
3. Results
4. Discussion
4.1. Comparisons
4.2. Relevance of Predictors and Predictor–Response Spatiotemporal Variance
4.3. Potential Improvements and Future Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Landscape | Model | Canopy Fuel Variable | N | RMSE | MAE | R² |
|---|---|---|---|---|---|---|
| Mt. Baker | Local | CC | 43,636 | 9.34% | 6.63% | 0.862 |
| Mt. Baker | Global | CC | 43,636 | 9.84% | 7.27% | 0.846 |
| Mt. Baker | FRG 5 | CC | 42,840 | 9.79% | 7.16% | 0.844 |
| Mt. Baker | Local | CH | 43,636 | 5.36 m | 3.86 m | 0.83 |
| Mt. Baker | Global | CH | 43,636 | 5.96 m | 4.33 m | 0.747 |
| Mt. Baker | FRG 5 | CH | 42,840 | 5.44 m | 3.97 m | 0.822 |
| Mt. Baker | Local | CBH | 43,636 | 2.16 m | 1.57 m | 0.79 |
| Mt. Baker | Global | CBH | 43,636 | 2.35 m | 1.74 m | 0.747 |
| Mt. Baker | FRG 5 | CBH | 42,840 | 2.29 m | 1.68 m | 0.759 |
| Mt. Baker | Local | CBD | 43,636 | 0.057 kg/m3 | 0.040 kg/m3 | 0.8 |
| Mt. Baker | Global | CBD | 43,636 | 0.063 kg/m3 | 0.045 kg/m3 | 0.749 |
| Mt. Baker | FRG 5 | CBD | 42,840 | 0.060 kg/m3 | 0.043 kg/m3 | 0.77 |
| Blackfoot-Swan | Local | CC | 175,639 | 8.11% | 5.93% | 0.839 |
| Blackfoot-Swan | Global | CC | 175,639 | 8.55% | 6.36% | 0.822 |
| Blackfoot-Swan | FRG 1 | CC | 85,805 | 8.19% | 6.08% | 0.819 |
| Blackfoot-Swan | FRG 3 | CC | 45,767 | 8.69% | 6.35% | 0.84 |
| Blackfoot-Swan | FRG 4 | CC | 41,856 | 8.50% | 6.17% | 0.82 |
| Blackfoot-Swan | Local | CH | 175,639 | 3.37 m | 2.47 m | 0.757 |
| Blackfoot-Swan | Global | CH | 175,639 | 3.84 m | 2.85 m | 0.686 |
| Blackfoot-Swan | FRG 1 | CH | 85,805 | 3.65 m | 2.72 m | 0.662 |
| Blackfoot-Swan | FRG 3 | CH | 45,767 | 3.89 m | 2.87 m | 0.732 |
| Blackfoot-Swan | FRG 4 | CH | 41,856 | 3.70 m | 2.74 m | 0.726 |
| Blackfoot-Swan | Local | CBH | 175,639 | 1.54 m | 1.13 m | 0.645 |
| Blackfoot-Swan | Global | CBH | 175,639 | 1.68 m | 1.25 m | 0.586 |
| Blackfoot-Swan | FRG 1 | CBH | 85,805 | 1.64 m | 1.23 m | 0.588 |
| Blackfoot-Swan | FRG 3 | CBH | 45,767 | 1.73 m | 1.28 m | 0.597 |
| Blackfoot-Swan | FRG 4 | CBH | 41,856 | 1.51 m | 1.11 m | 0.655 |
| Blackfoot-Swan | Local | CBD | 175,639 | 0.049 kg/m3 | 0.032 kg/m3 | 0.723 |
| Blackfoot-Swan | Global | CBD | 175,639 | 0.047 kg/m3 | 0.034 kg/m3 | 0.712 |
| Blackfoot-Swan | FRG 1 | CBD | 85,805 | 0.045 kg/m3 | 0.032 kg/m3 | 0.702 |
| Blackfoot-Swan | FRG 3 | CBD | 45,767 | 0.048 kg/m3 | 0.035 kg/m3 | 0.736 |
| Blackfoot-Swan | FRG 4 | CBD | 41,856 | 0.047 kg/m3 | 0.034 kg/m3 | 0.712 |
| Clear Creek | Local | CC | 21,060 | 10.24% | 7.71% | 0.72 |
| Clear Creek | Global | CC | 21,060 | 10.44% | 8.00% | 0.718 |
| Clear Creek | FRG 3 | CC | 17,122 | 9.91% | 7.35% | 0.732 |
| Clear Creek | Local | CH | 21,060 | 4.84 m | 3.56 m | 0.788 |
| Clear Creek | Global | CH | 21,060 | 5.43 m | 4.03 m | 0.734 |
| Clear Creek | FRG 3 | CH | 17,122 | 5.17 m | 3.80 m | 0.768 |
| Clear Creek | Local | CBH | 21,060 | 2.67 m | 1.93 m | 0.628 |
| Clear Creek | Global | CBH | 21,060 | 2.85 m | 2.11 m | 0.586 |
| Clear Creek | FRG 3 | CBH | 17,122 | 2.87 m | 2.15 m | 0.589 |
| Clear Creek | Local | CBD | 21,060 | 0.065 kg/m3 | 0.049 kg/m3 | 0.631 |
| Clear Creek | Global | CBD | 21,060 | 0.069 kg/m3 | 0.052 kg/m3 | 0.598 |
| Clear Creek | FRG 3 | CBD | 17,122 | 0.069 kg/m3 | 0.053 kg/m3 | 0.577 |
| Dinkey | Local | CC | 41,443 | 10.42% | 7.91% | 0.748 |
| Dinkey | Global | CC | 41,443 | 10.60% | 8.19% | 0.739 |
| Dinkey | FRG 1 | CC | 33,790 | 10.43% | 7.99% | 0.73 |
| Dinkey | FRG 3 | CC | 6989 | 10.17% | 7.75% | 0.765 |
| Dinkey | Local | CH | 41,443 | 6.60 m | 5.05 m | 0.702 |
| Dinkey | Global | CH | 6.88 | 6.88 m | 5.31 m | 0.675 |
| Dinkey | FRG 1 | CH | 33,790 | 7.31 m | 5.67 m | 0.64 |
| Dinkey | FRG 3 | CH | 6989 | 6.80 m | 5.23 m | 0.563 |
| Dinkey | Local | CBH | 41,443 | 2.60 m | 1.95 m | 0.551 |
| Dinkey | Global | CBH | 41,443 | 2.73 m | 2.07 m | 0.508 |
| Dinkey | FRG 1 | CBH | 33,790 | 2.75 m | 2.07 m | 0.51 |
| Dinkey | FRG 3 | CBH | 6989 | 2.86 m | 2.27 m | 0.355 |
| Dinkey | Local | CBD | 41,443 | 0.057 kg/m3 | 0.038 kg/m3 | 0.666 |
| Dinkey | Global | CBD | 41,443 | 0.057 kg/m3 | 0.039 kg/m3 | 0.667 |
| Dinkey | FRG 1 | CBD | 33790 | 0.059 kg/m3 | 0.041 kg/m3 | 0.659 |
| Dinkey | FRG 3 | CBD | 6989 | 0.042 kg/m3 | 0.026 kg/m3 | 0.667 |
| Garcia | Local | CC | 5522 | 8.99% | 6.16% | 0.216 |
| Garcia | Global | CC | 5522 | 8.56% | 6.24% | 0.269 |
| Garcia | FRG 1 | CC | 5493 | 7.98% | 5.30% | 0.363 |
| Garcia | Local | CH | 5522 | 4.72 m | 3.57 m | 0.152 |
| Garcia | Global | CH | 41,443 | 5.02 m | 3.81 m | 0.081 |
| Garcia | FRG 1 | CH | 5493 | 5.13 m | 3.92 m | 0.041 |
| Garcia | Local | CBH | 5522 | 2.29 m | 1.78 m | 0.423 |
| Garcia | Global | CBH | 5522 | 2.40 m | 1.88 m | 0.368 |
| Garcia | FRG 1 | CBH | 5493 | 2.40 m | 1.88 m | 0.365 |
| Garcia | Local | CBD | 5522 | 0.081 kg/m3 | 0.064 kg/m3 | 0.284 |
| Garcia | Global | CBD | 41,443 | 0.080 kg/m3 | 0.064 kg/m3 | 0.305 |
| Garcia | FRG 1 | CBD | 5493 | 0.079 kg/m3 | 0.062 kg/m3 | 0.325 |
| Grand Canyon | Local | CC | 10,548 | 7.09% | 5.30% | 0.738 |
| Grand Canyon | Global | CC | 10,548 | 7.32% | 5.51% | 0.717 |
| Grand Canyon | FRG 1 | CC | 7629 | 7.31% | 5.50% | 0.716 |
| Grand Canyon | FRG 4 | CC | 2671 | 6.82% | 5.05% | 0.725 |
| Grand Canyon | Local | CH | 10,548 | 3.09 m | 2.32 m | 0.663 |
| Grand Canyon | Global | CH | 10,548 | 3.13 m | 2.37 m | 0.673 |
| Grand Canyon | FRG 1 | CH | 7629 | 3.23 m | 2.45 m | 0.674 |
| Grand Canyon | FRG 4 | CH | 2671 | 3.13 m | 2.38 m | 0.487 |
| Grand Canyon | Local | CBH | 10,548 | 2.06 m | 1.55 m | 0.822 |
| Grand Canyon | Global | CBH | 10,548 | 2.21 m | 1.69 m | 0.792 |
| Grand Canyon | FRG 1 | CBH | 7629 | 2.37 m | 1.82 m | 0.759 |
| Grand Canyon | FRG 4 | CBH | 2671 | 1.69 m | 1.30 m | 0.668 |
| Grand Canyon | Local | CBD | 10,548 | 0.028 kg/m3 | 0.021 kg/m3 | 0.556 |
| Grand Canyon | Global | CBD | 10,548 | 0.030 kg/m3 | 0.021 kg/m3 | 0.506 |
| Grand Canyon | FRG 1 | CBD | 7629 | 0.030 kg/m3 | 0.022 kg/m3 | 0.509 |
| Grand Canyon | FRG 4 | CBD | 2671 | 0.022 kg/m3 | 0.017 kg/m3 | 0.654 |
| Grand County | Local | CC | 74,132 | 9.87% | 7.20% | 0.76 |
| Grand County | Global | CC | 74,132 | 10.03% | 7.43% | 0.753 |
| Grand County | FRG 1 | CC | 14,605 | 12.08% | 9.01% | 0.696 |
| Grand County | FRG 4 | CC | 55,336 | 9.49% | 6.95% | 0.745 |
| Grand County | Local | CH | 74,132 | 3.02 m | 2.25 m | 0.619 |
| Grand County | Global | CH | 74,132 | 3.22 m | 2.39 m | 0.566 |
| Grand County | FRG 1 | CH | 14,605 | 3.73 m | 2.85 m | 0.421 |
| Grand County | FRG 4 | CH | 55,336 | 3.01 m | 2.23 m | 0.581 |
| Grand County | Local | CBH | 74,132 | 1.33 m | 0.98 m | 0.552 |
| Grand County | Global | CBH | 74,132 | 1.48 m | 1.08 m | 0.448 |
| Grand County | FRG 1 | CBH | 14,605 | 1.68 m | 1.26 m | 0.387 |
| Grand County | FRG 4 | CBH | 55,336 | 1.30 m | 0.96 m | 0.531 |
| Grand County | Local | CBD | 74,132 | 0.043 kg/m3 | 0.030 kg/m3 | 0.599 |
| Grand County | Global | CBD | 74,132 | 0.044 kg/m3 | 0.031 kg/m3 | 0.587 |
| Grand County | FRG 1 | CBD | 14,605 | 0.049 kg/m3 | 0.033 kg/m3 | 0.545 |
| Grand County | FRG 4 | CBD | 55,336 | 0.042 kg/m3 | 0.031 kg/m3 | 0.585 |
| Hoh | Local | CC | 62,288 | 12.93% | 9.71% | 0.61 |
| Hoh | Global | CC | 62,288 | 11.23% | 8.03% | 0.712 |
| Hoh | FRG 5 | CC | 62,016 | 11.50% | 8.35% | 0.697 |
| Hoh | Local | CH | 62,288 | 5.75 m | 4.13 m | 0.871 |
| Hoh | Global | CH | 62,288 | 6.42 m | 4.68 m | 0.841 |
| Hoh | FRG 5 | CH | 62,016 | 5.89 m | 4.27 m | 0.865 |
| Hoh | Local | CBH | 62,288 | 3.28 m | 2.45 m | 0.67 |
| Hoh | Global | CBH | 62,288 | 3.78 m | 2.87 m | 0.564 |
| Hoh | FRG 5 | CBH | 62,016 | 3.73 m | 2.84 m | 0.575 |
| Hoh | Local | CBD | 62,288 | 0.080 kg/m3 | 0.059 kg/m3 | 0.644 |
| Hoh | Global | CBD | 62,288 | 0.084 kg/m3 | 0.062 kg/m3 | 0.607 |
| Hoh | FRG 5 | CBD | 62,016 | 0.083 kg/m3 | 0.062 kg/m3 | 0.617 |
| Ochoco | Local | CC | 122,339 | 8.52% | 6.46% | 0.79 |
| Ochoco | Global | CC | 122,339 | 8.60% | 6.60% | 0.787 |
| Ochoco | FRG 1 | CC | 93,212 | 8.53% | 6.49% | 0.782 |
| Ochoco | FRG 3 | CC | 22,380 | 8.53% | 6.50% | 0.778 |
| Ochoco | Local | CH | 122,339 | 4.86 m | 3.73 m | 0.646 |
| Ochoco | Global | CH | 122,339 | 5.08 m | 3.93 m | 0.615 |
| Ochoco | FRG 1 | CH | 93,212 | 5.13 m | 4.00 m | 0.564 |
| Ochoco | FRG 3 | CH | 22,380 | 4.68 m | 3.53 m | 0.704 |
| Ochoco | Local | CBH | 122,339 | 1.91 m | 1.41 m | 0.501 |
| Ochoco | Global | CBH | 122,339 | 1.95 m | 1.44 m | 0.47 |
| Ochoco | FRG 1 | CBH | 93,212 | 2.01 m | 1.50 m | 0.448 |
| Ochoco | FRG 3 | CBH | 22,380 | 1.78 m | 1.27 m | 0.53 |
| Ochoco | Local | CBD | 122,339 | 0.031 kg/m3 | 0.022 kg/m3 | 0.585 |
| Ochoco | Global | CBD | 122,339 | 0.030 kg/m3 | 0.021 kg/m3 | 0.608 |
| Ochoco | FRG 1 | CBD | 93,212 | 0.031 kg/m3 | 0.022 kg/m3 | 0.598 |
| Ochoco | FRG 3 | CBD | 22,380 | 0.028 kg/m3 | 0.019 kg/m3 | 0.555 |
| Powell | Local | CC | 55,239 | 8.81% | 6.52% | 0.859 |
| Powell | Global | CC | 55,239 | 9.46% | 7.17% | 0.837 |
| Powell | FRG 3 | CC | 24,599 | 10.04% | 7.54% | 0.83 |
| Powell | FRG 4 | CC | 28,985 | 8.10% | 6.03% | 0.835 |
| Powell | Local | CH | 55,239 | 4.44 m | 3.33 m | 0.752 |
| Powell | Global | CH | 55,239 | 4.76 m | 3.58 m | 0.718 |
| Powell | FRG 3 | CH | 24,599 | 4.90 m | 3.67 m | 0.75 |
| Powell | FRG 4 | CH | 28,985 | 4.06 m | 3.05 m | 0.739 |
| Powell | Local | CBH | 55,239 | 2.13 m | 1.54 m | 0.533 |
| Powell | Global | CBH | 55,239 | 2.10 m | 1.49 m | 0.545 |
| Powell | FRG 3 | CBH | 24,599 | 2.31 m | 1.64 m | 0.588 |
| Powell | FRG 4 | CBH | 28,985 | 1.76 m | 1.28 m | 0.54 |
| Powell | Local | CBD | 55,239 | 0.054 kg/m3 | 0.037 kg/m3 | 0.59 |
| Powell | Global | CBD | 55,239 | 0.051 kg/m3 | 0.035 kg/m3 | 0.635 |
| Powell | FRG 3 | CBD | 24,599 | 0.062 kg/m3 | 0.045 kg/m3 | 0.603 |
| Powell | FRG 4 | CBD | 28,985 | 0.036 kg/m3 | 0.024 kg/m3 | 0.61 |
| Southern Coast | Local | CC | 491,731 | 16.35% | 12.32% | 0.613 |
| Southern Coast | Global | CC | 491,731 | 15.75% | 11.19% | 0.642 |
| Southern Coast | FRG 1 | CC | 125,537 | 15.97% | 11.11% | 0.684 |
| Southern Coast | FRG 3 | CC | 83,831 | 13.30% | 8.60% | 0.731 |
| Southern Coast | FRG 5 | CC | 281,017 | 16.81% | 12.09% | 0.554 |
| Southern Coast | Local | CH | 491,731 | 7.31 m | 5.30 m | 0.78 |
| Southern Coast | Global | CH | 491,731 | 8.39 m | 6.19 m | 0.709 |
| Southern Coast | FRG 1 | CH | 125,537 | 7.37 m | 5.51 m | 0.634 |
| Southern Coast | FRG 3 | CH | 83,831 | 7.90 m | 5.64 m | 0.721 |
| Southern Coast | FRG 5 | CH | 281,017 | 8.47 m | 6.27 m | 0.738 |
| Southern Coast | Local | CBH | 491,731 | 4.00 m | 3.00 m | 0.575 |
| Southern Coast | Global | CBH | 491,731 | 4.41 m | 3.36 m | 0.485 |
| Southern Coast | FRG 1 | CBH | 125,537 | 3.33 m | 2.50 m | 0.555 |
| Southern Coast | FRG 3 | CBH | 83,831 | 4.37 m | 3.31 m | 0.54 |
| Southern Coast | FRG 5 | CBH | 281,017 | 4.70 m | 3.60m | 0.448 |
| Southern Coast | Local | CBD | 491,731 | 0.107 kg/m3 | 0.077 kg/m3 | 0.552 |
| Southern Coast | Global | CBD | 491,731 | 0.120 kg/m3 | 0.087 kg/m3 | 0.431 |
| Southern Coast | FRG 1 | CBD | 125,537 | 0.123 kg/m3 | 0.090 kg/m3 | 0.478 |
| Southern Coast | FRG 3 | CBD | 83,831 | 0.110 kg/m3 | 0.079 kg/m3 | 0.52 |
| Southern Coast | FRG 5 | CBD | 281,017 | 0.118 kg/m3 | 0.084 kg/m3 | 0.431 |
| Tahoe | Local | CC | 420,960 | 9.64% | 7.09% | 0.874 |
| Tahoe | Global | CC | 420,960 | 10.51% | 7.98% | 0.85 |
| Tahoe | FRG 1 | CC | 337,658 | 10.35% | 7.64% | 0.853 |
| Tahoe | FRG 3 | CC | 76,895 | 9.98% | 7.55% | 0.818 |
| Tahoe | Local | CH | 420,960 | 5.96 m | 4.54 m | 0.667 |
| Tahoe | Global | CH | 420,960 | 6.35 m | 4.90 m | 0.622 |
| Tahoe | FRG 1 | CH | 337,658 | 6.67 m | 5.18 m | 0.591 |
| Tahoe | FRG 3 | CH | 76,895 | 5.82 m | 4.44 m | 0.63 |
| Tahoe | Local | CBH | 420,960 | 2.28 m | 1.69 m | 0.587 |
| Tahoe | Global | CBH | 420,960 | 2.41 m | 1.79 m | 0.541 |
| Tahoe | FRG 1 | CBH | 337,658 | 2.51 m | 1.86 m | 0.53 |
| Tahoe | FRG 3 | CBH | 76,895 | 2.15 m | 1.63 m | 0.484 |
| Tahoe | Local | CBD | 420,960 | 0.053 kg/m3 | 0.036 kg/m3 | 0.789 |
| Tahoe | Global | CBD | 420,960 | 0.054 kg/m3 | 0.037 kg/m3 | 0.775 |
| Tahoe | FRG 1 | CBD | 337,658 | 0.058 kg/m3 | 0.040 kg/m3 | 0.761 |
| Tahoe | FRG 3 | CBD | 76,895 | 0.038 kg/m3 | 0.025 kg/m3 | 0.75 |
| Teanaway | Local | CC | 25,817 | 10.01% | 7.48% | 0.8 |
| Teanaway | Global | CC | 25,817 | 10.41% | 7.91% | 0.785 |
| Teanaway | FRG 1 | CC | 6102 | 10.29% | 7.78% | 0.702 |
| Teanaway | FRG 3 | CC | 19,181 | 10.04% | 7.54% | 0.809 |
| Teanaway | Local | CH | 25,817 | 4.51 m | 3.54 m | 0.509 |
| Teanaway | Global | CH | 25,817 | 4.52 m | 3.51 m | 0.533 |
| Teanaway | FRG 1 | CH | 6102 | 4.32 m | 3.32 m | 0.419 |
| Teanaway | FRG 3 | CH | 19,181 | 4.23 m | 3.26 m | 0.611 |
| Teanaway | Local | CBH | 25,817 | 2.03 m | 1.53 m | 0.525 |
| Teanaway | Global | CBH | 25,817 | 2.14 m | 1.62 m | 0.47 |
| Teanaway | FRG 1 | CBH | 6102 | 2.16 m | 1.64 m | 0.451 |
| Teanaway | FRG 3 | CBH | 19,181 | 2.04 m | 1.55 m | 0.521 |
| Teanaway | Local | CBD | 25,817 | 0.042 kg/m3 | 0.030 kg/m3 | 0.667 |
| Teanaway | Global | CBD | 25,817 | 0.043 kg/m3 | 0.031 kg/m3 | 0.645 |
| Teanaway | FRG 1 | CBD | 6102 | 0.038 kg/m3 | 0.026 kg/m3 | 0.501 |
| Teanaway | FRG 3 | CBD | 19,181 | 0.044 kg/m3 | 0.032 kg/m3 | 0.662 |
| Landscape | Model | Canopy Fuel Variable | N | RMSE | MAE | R² |
|---|---|---|---|---|---|---|
| Illilouette | Dinkey | CC | 124,229 | 10.95% | 8.53% | 0.680 |
| Illilouette | Global | CC | 124,229 | 10.68% | 8.31% | 0.696 |
| Illilouette | FRG 1 | CC | 59,941 | 11.51% | 9.05% | 0.684 |
| Illilouette | FRG 3 | CC | 59,606 | 9.56% | 7.36% | 0.717 |
| Illilouette | Dinkey | CH | 124,229 | 8.06 m | 6.28 m | 0.300 |
| Illilouette | Global | CH | 124,229 | 7.84 m | 6.18 m | 0.338 |
| Illilouette | FRG 1 | CH | 59,941 | 8.81 m | 6.90 m | 0.280 |
| Illilouette | FRG 3 | CH | 59,606 | 7.40 m | 5.96 m | 0.191 |
| Illilouette | Dinkey | CBH | 124,229 | 4.25 m | 3.16 m | −0.168 |
| Illilouette | Global | CBH | 124,229 | 4.11 m | 3.03 m | −0.094 |
| Illilouette | FRG 1 | CBH | 59,941 | 4.77 m | 3.49 m | −0.120 |
| Illilouette | FRG 3 | CBH | 59,606 | 3.35 m | 2.55 m | −0.094 |
| Illilouette | Dinkey | CBD | 124,229 | 0.035 kg/m3 | 0.024 kg/m3 | 0.417 |
| Illilouette | Global | CBD | 124,229 | 0.030 kg/m3 | 0.020 kg/m3 | 0.578 |
| Illilouette | FRG 1 | CBD | 59,941 | 0.033 kg/m3 | 0.022 kg/m3 | 0.540 |
| Illilouette | FRG 3 | CBD | 59,606 | 0.029 kg/m3 | 0.019 kg/m3 | 0.529 |
| North Coast | South Coast | CC | 947,615 | 15.93% | 12.47% | 0.553 |
| North Coast | Global | CC | 947,615 | 14.22% | 10.76% | 0.644 |
| North Coast | FRG 3 | CC | 49,945 | 14.05% | 9.73% | 0.692 |
| North Coast | FRG 5 | CC | 895,207 | 14.33% | 10.24% | 0.631 |
| North Coast | South Coast | CH | 947,615 | 7.83 m | 5.98 m | 0.702 |
| North Coast | Global | CH | 947,615 | 8.15 m | 6.27 m | 0.677 |
| North Coast | FRG 3 | CH | 49,945 | 9.05 m | 6.80 m | 0.565 |
| North Coast | FRG 5 | CH | 895,207 | 10.04 m | 7.61 m | 0.510 |
| North Coast | South Coast | CBH | 947,615 | 4.65 m | 3.59 m | 0.430 |
| North Coast | Global | CBH | 947,615 | 4.66 m | 3.64 m | 0.428 |
| North Coast | FRG 3 | CBH | 49,945 | 4.37 m | 3.44 m | 0.433 |
| North Coast | FRG 5 | CBH | 895,207 | 4.94 m | 3.82 m | 0.359 |
| North Coast | South Coast | CBD | 947,615 | 0.116 kg/m3 | 0.085 kg/m3 | 0.511 |
| North Coast | Global | CBD | 947,615 | 0.121 kg/m3 | 0.090 kg/m3 | 0.465 |
| North Coast | FRG 3 | CBD | 49,945 | 0.125 kg/m3 | 0.092 kg/m3 | 0.510 |
| North Coast | FRG 5 | CBD | 895,207 | 0.126 kg/m3 | 0.095 kg/m3 | 0.417 |
| Slate Creek | Clear Creek | CC | 320,971 | 25.29% | 22.28% | −0.446 |
| Slate Creek | Global | CC | 320,971 | 14.96% | 12.18% | 0.494 |
| Slate Creek | FRG 1 | CC | 55,873 | 13.90% | 10.74% | 0.633 |
| Slate Creek | FRG 3 | CC | 190,294 | 14.62% | 11.68% | 0.561 |
| Slate Creek | FRG 4 | CC | 73,862 | 15.49% | 13.02% | −0.057 |
| Slate Creek | Clear Creek | CH | 320,971 | 7.05 m | 5.52 m | 0.249 |
| Slate Creek | Global | CH | 320,971 | 6.36 m | 4.90 m | 0.390 |
| Slate Creek | FRG 1 | CH | 55,873 | 7.23 m | 5.72 m | 0.397 |
| Slate Creek | FRG 3 | CH | 190,294 | 6.62 m | 5.13 m | 0.345 |
| Slate Creek | FRG 4 | CH | 73,862 | 5.91 m | 4.65 m | −0.099 |
| Slate Creek | Clear Creek | CBH | 320,971 | 3.84 m | 2.84 m | −0.004 |
| Slate Creek | Global | CBH | 320,971 | 3.58 m | 2.69 m | 0.125 |
| Slate Creek | FRG 1 | CBH | 55,873 | 4.33 m | 3.36 m | 0.142 |
| Slate Creek | FRG 3 | CBH | 190,294 | 3.72 m | 2.81 m | 0.070 |
| Slate Creek | FRG 4 | CBH | 73,862 | 2.75 m | 2.23 m | −0.411 |
| Slate Creek | Clear Creek | CBD | 320,971 | 0.114 kg/m3 | 0.080 kg/m3 | −0.889 |
| Slate Creek | Global | CBD | 320,971 | 0.060 kg/m3 | 0.045 kg/m3 | 0.479 |
| Slate Creek | FRG 1 | CBD | 55,873 | 0.060 kg/m3 | 0.045 kg/m3 | 0.503 |
| Slate Creek | FRG 3 | CBD | 190,294 | 0.063 kg/m3 | 0.047 kg/m3 | 0.473 |
| Slate Creek | FRG 4 | CBD | 73,862 | 0.054 kg/m3 | 0.042 kg/m3 | 0.198 |
References
- Ellsworth, D.S.; Reich, P.B. Canopy structure and vertical patterns of photosynthesis and related leaf traits in a deciduous forest. Oecologia 1993, 96, 169–178. [Google Scholar] [CrossRef]
- Franklin, J.F.; Spies, T.A.; Van Pelt, R.; Carey, A.B.; Thornburgh, D.A.; Berg, D.R.; Lindenmayer, D.B.; Harmon, M.E.; Keeton, W.S.; Shaw, D.C.; et al. Disturbance and structural development of natural forest ecosystems with silvicultural implications, using Douglas-fir forests as an example. For. Ecol. Manag. 2002, 155, 399–423. [Google Scholar] [CrossRef]
- Shugart, H.H.; Saatchi, S.; Hall, F.G. Importance of structure and its measurement in quantifying function of forest ecoystems. J. Geophys. Res. 2010, 115, 1–16. [Google Scholar] [CrossRef]
- Moran, C.J.; Rowell, E.M.; Seielstad, C.A. A data-driven framework to identify and compare forest structure classes using LiDAR. Remote Sens. Environ. 2018, 211, 154–166. [Google Scholar] [CrossRef]
- Kane, V.R.; Bartl-Geller, B.N.; North, M.P.; Kane, J.T.; Lydersen, J.M.; Jeronimo, S.M.A.; Collins, B.M.; Moskal, L.M. First-entry wildfires can create opening and tree clump patterns characteristic of resilient forests. For. Ecol. Manag. 2019, 454, 117659. [Google Scholar] [CrossRef]
- Shang, C.; Coops, N.C.; Wulder, M.A.; White, J.C.; Hermosilla, T. Update and spatial extension of strategic forest inventories using time series remote sensing and modeling. Int. J. Appl. Earth Obs. 2020, 84, 101956. [Google Scholar] [CrossRef]
- Wulder, M.A.; Hall, R.J.; Coops, N.C.; Franklin, S.E. High spatial resolution remotely sensed data for ecosystem characterization. BioScience 2004, 54, 511–521. [Google Scholar] [CrossRef] [Green Version]
- Collins, B.M.; Stephens, S.L.; Roller, G.B.; Battles, J.J. Simulating fire and forest dynamics for a landscape fuel treatment project in the Sierra Nevada. For. Sci. 2011, 57, 77–88. [Google Scholar]
- Cochrane, M.A.; Moran, C.J.; Wimberly, M.C.; Baer, A.D.; Finney, M.A.; Beckendorf, K.L.; Eidenshink, J.; Zhu, Z. Estimation of wildfire size and risk changes due to fuels treatments. Int. J. Wildland Fire 2012, 21, 357–367. [Google Scholar] [CrossRef] [Green Version]
- Ryan, K.C.; Opperman, T.S. LANDFIRE—A national vegetation/fuels data base for use in fuels treatment, restoration, and suppression planning. For. Ecol. Manag. 2013, 294, 208–216. [Google Scholar] [CrossRef] [Green Version]
- Drury, S.A.; Rauscher, H.M.; Banwell, E.M.; Huang, S.; Lavezzo, T.L. The interagency fuels treatment decision support system: Functionality for fuels treatment planning. Fire Ecol. 2016, 12, 103–123. [Google Scholar] [CrossRef] [Green Version]
- Wiedinmyer, C.; Hurteau, M.D. Prescribed fire as a means of reducing forest carbon emissions in the western United States. Environ. Sci. Tech. 2010, 44, 1926–1932. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Calkin, D.E.; Gebert, K.M.; Venn, T.J.; Silverstein, R.P. Factors influencing large wildland fire suppression expenditures. Int. J. Wildland Fire 2008, 17, 650–659. [Google Scholar] [CrossRef]
- Calkin, D.E.; Thompson, M.P.; Finney, M.A.; Hyde, K.D. A real-time risk assessment tool supporting wildland fire decisionmaking. J. For. 2011, 109, 274–280. [Google Scholar]
- Ager, A.A.; Vaillant, N.M.; Finney, M.A.; Preisler, H.K. Analyzing wildfire exposure and source-sink relationships on a fire prone forest landscape. For. Ecol. Manag. 2012, 267, 271–283. [Google Scholar] [CrossRef]
- Rollins, M.G. LANDFIRE: A nationally consistent vegetation, wildland fire, and fuel assessment. Int. J. Wildland Fire 2009, 18, 235–249. [Google Scholar] [CrossRef] [Green Version]
- Noonan-Wright, E.K.; Opperman, T.S.; Finney, M.A.; Zimmerman, G.T.; Seli, R.C.; Elenz, L.M.; Calkin, D.E.; Fielder, J.R. Developing the US Wildland Fire Decision Support System. J. Combust. 2011, 2011, 168473. [Google Scholar] [CrossRef]
- Williams, J. Exploring the onset of high-impact mega-fires through a forest land management prism. For. Ecol. Manag. 2013, 294, 4–10. [Google Scholar] [CrossRef]
- Fidelis, A.; Alvarado, S.T.; Barradas, A.C.S.; Pivello, V.R. The year 2017: Megafires and management in the Cerrado. Fire 2018, 1, 49. [Google Scholar] [CrossRef] [Green Version]
- Syphard, A.D.; Keeley, J.E. Factors associated with structure loss in the 2013-2018 California wildfires. Fire 2019, 2, 49. [Google Scholar] [CrossRef] [Green Version]
- Abatzoglou, J.T.; Williams, A.P. Impact of anthropogenic climate change on wildfire across western US forests. Proc. Natl. Acad. Sci. USA 2016, 113, 11770–11775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schoennagel, T.; Balch, J.K.; Brenkert-Smith, H.; Dennison, P.E.; Harvey, B.J.; Krawchuk, M.A.; Mietkiewicz, N.; Morgan, P.; Moritz, M.A.; Rasker, R.; et al. Adapt to more wildfire in western North American forests as climate changes. Proc. Natl. Acad. Sci. USA 2017, 114, 4582–4590. [Google Scholar] [CrossRef] [Green Version]
- McRoberts, R.E.; Tomppo, E.; Naesset, E. Advances and emerging issues in national forest inventories. Scand. J. For. Res. 2010, 25, 368–381. [Google Scholar] [CrossRef]
- Tomppo, E.; Olsson, H.; Stahl, G.; Nilsson, M.; Hagner, O.; Katila, M. Combining national forest inventory field plot and remote sensing data for forest databases. Remote Sens. Environ. 2008, 112, 1982–1999. [Google Scholar] [CrossRef]
- Makela, H.; Pekkarinen, A. Estimation of forest stand volumes by Landsat TM imagery and stand-level field-inventory data. For. Ecol. Manag. 2004, 196, 245–255. [Google Scholar] [CrossRef]
- Ohmann, J.L.; Gregory, M.J.; Roberts, H.M. Scale considerations for integrating forest inventory plot data and satellite image data for regional forest mapping. Remote Sens. Environ. 2014, 151, 3–15. [Google Scholar] [CrossRef]
- Hu, T.; Su, Y.; Xue, B.; Liu, J.; Zhao, X.; Fang, J.; Guo, Q. Mapping global forest aboveground biomass with spaceborne LiDAR, optical imagery, and forest inventory data. Remote Sens. 2016, 8, 565. [Google Scholar] [CrossRef] [Green Version]
- Hawbaker, T.J.; Keuler, N.S.; Lesak, A.A.; Gobakken, T.; Contrucci, K.; Radeloff, V.C. Improved estimates of forest vegetation structure and biomass with a LiDAR-optimized sampling design. J. Geophys. Res. 2009, 114, G00E04. [Google Scholar] [CrossRef]
- Maltamo, M.; Bollandsas, O.M.; Gobakken, T.; Naesset, E. Large-scale prediction of aboveground biomass in heterogeneous mountain forests by means of airborne laser scanning. Can. J. For. Res. 2016, 46, 1138–1144. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef] [Green Version]
- Kane, V.R.; McGaughey, R.J.; Bakker, J.D.; Gersonde, R.F.; Lutz, J.A.; Franklin, J.F. Comparisons between field- and LiDAR-based measures of stand structural complexity. Can. J. For. Res. 2010, 40, 761–773. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. Lidar remote sensing of above-ground biomass in three biomes. Glob. Ecol. Biogeogr. 2002, 11, 393–399. [Google Scholar] [CrossRef] [Green Version]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J. Generalizing predictive models of forestry inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Strunk, J.L.; Temesgen, H.; Andersen, H.-E.; Packalen, P. Prediction of forest attributes with field plots, Landsat, and a sample of lidar strips: A case study on the Kenai Peninsula, Alaska. Photogramm. Eng. Remote Sens. 2014, 2, 143–150. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [Green Version]
- Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integrationg of lidar and Landsat ETM+ data for estimating and mapping forest canopy height. Remote Sens. Environ. 2002, 82, 397–416. [Google Scholar] [CrossRef] [Green Version]
- Hyde, P.; Dubayah, R.; Walker, W.; Blair, J.B.; Hofton, M.; Hunsaker, C. Mapping forest structure for wildlife habitat analysis using multi-sensor (LiDAR, SAR/InSAR, ETM+, Quickbird) synergy. Remote Sens. Environ. 2006, 102, 63–73. [Google Scholar] [CrossRef]
- Pascual, C.; Garcia-Abril, A.; Cohen, W.B.; Martin-Fernandez, S. Relationship between LiDAR-derived forest canopy height and Landsat images. Int. J. Remote Sens. 2010, 31, 1261–1280. [Google Scholar] [CrossRef]
- Stojanova, D.; Panov, P.; Gjorgjioski, V.; Kobler, A.; Dzeroski, S. Estimating vegetation height and canopy cover from remotely sensed data with machine learning. Ecol. Inf. 2010, 5, 256–266. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; White, J.C. Characterizing stand-level forest canopy cover and height using Landsat time series, samples of airborne LiDAR, and the random forest algorithm. ISPRS J. Photogramm. 2015, 101, 89–101. [Google Scholar] [CrossRef]
- Wilkes, P.; Jones, S.D.; Suarez, L.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Haywood, A.; Skidmore, A.K. Mapping forest canopy height across large areas by upscaling ALS estimates with freely available satellite data. Remote Sens. 2015, 7, 12563–12587. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.C.; Potapov, P.V.; Goetz, S.J.; Turubanova, S.; Tyukavina, A.; Krylov, A.; Kommareddy, A.; Egorov, A. Mapping tree height distributions in Sub-Saharan Africa using Landsat 7 and 8 data. Remote Sens. Environ. 2016, 185, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Frazier, R.J.; Coops, N.C.; Wulder, M.A.; Kennedy, R. Characterization of aboveground biomass in an unmanaged boreal forest using Landsat temporal segmentation metrics. ISPRS J. Photogramm. 2014, 92, 137–146. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Turner, D.P.; Guzy, M.; Cohen, W.B. Combining lidar estimates of aboveground biomass and Landsat estimates of stand age for spatially extensive validation of modeled forest productivity. Remote Sens. Environ. 2005, 95, 549–558. [Google Scholar] [CrossRef]
- Margolis, H.A.; Nelson, R.F.; Montesano, P.M.; Beaudoin, A.; Sun, G.; Andersen, H.; Wulder, M.A. Combining satellite lidar, airborne lidar, and ground plots to estimate the amount and distribution of aboveground biomass in the boreal forest of North America. Can. J. For. Res. 2015, 45, 838–855. [Google Scholar] [CrossRef] [Green Version]
- Bell, D.M.; Gregory, M.J.; Kane, V.; Kane, J.; Kennedy, R.E.; Roberts, H.M.; Yang, Z. Multiscale divergence between Landsat and lidar-based biomass mapping is related to regional variation in canopy cover and composition. Carbon Balance Manag. 2018, 13, 15. [Google Scholar] [CrossRef] [Green Version]
- Zald, H.S.J.; Wulder, M.A.; White, J.C.; Hilker, T.; Hermosilla, T.; Hobart, G.W.; Coops, N.C. Integrating Landsat pixel composites and change metrics with lidar plots to predictively map forest structure and aboveground biomass in Saskatchewan, Canada. Remote Sens. Environ. 2016, 176, 188–201. [Google Scholar] [CrossRef] [Green Version]
- LaRue, E.A.; Atkins, J.W.; Dahlin, K.; Fahey, R.; Fei, S.; Gough, C.; Hardiman, B.S. Linking Landsat to terrestrial LiDAR: Vegetation metrics of forest greenness are correlated with canopy structural complexity. Int. J. Appl. Earth Obs. 2018, 73, 420–427. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S.J. Large-area mapping of Canadian boreal forest cover, height, biomass and other structural attributes using Landsat composites and lidar plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Cohen, W.B.; Spies, T.A. Estimating structural attributes of douglas-fir/western hemlock forest stands from Landsat and SPOT imagery. Remote Sens. Environ. 1992, 41, 1–17. [Google Scholar] [CrossRef]
- Reeves, M.C.; Ryan, K.C.; Rollins, M.G.; Thompson, T.G. Spatial fuel data products of the LANDFIRE project. Int. J. Wildland Fire 2009, 18, 250–267. [Google Scholar] [CrossRef]
- Peterson, B.; Nelson, K.J.; Seielstad, C.; Stoker, J.; Jolly, W.M.; Parsons, R. Automated integration of lidar into the LANDFIRE product suite. Remote Sens. Lett. 2015, 6, 247–256. [Google Scholar] [CrossRef]
- Andersen, H.; McGaughey, R.J.; Reutebuch, S.E. Estimating forest canopy fuel parameters using LIDAR data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Riano, D.; Chuvieco, E.; Condes, S.; Gonzalez-Matesanz, J.; Ustin, S.L. Generation of crown bulk density for Pinus sylvestris L. from Lidar. Remote Sens. Environ. 2004, 92, 345–352. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhao, K. A voxel-based lidar method for estimating crown base height for deciduous and pine trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
- Rowell, E. Estimating Forest Biophysical Variables from Airborne Laser Altimetry in a Ponderosa Pine Forest. Master’s Thesis, South Dakota School of Mines and Technology, Rapid City, SD, USA, 2005. [Google Scholar]
- Stratton, R.D. Guidebook on Landfire Fuels Data Acquisition, Critique, Modification, Maintenance, and Model Calibration; Technical Report No. RMRS-GTR-220; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2009; pp. 1–54.
- Lawrence, R.L.; Moran, C.J. The AmericaView classification methods accuracy comparison project: A rigorous approach for model selection. Remote Sens. Environ. 2015, 170, 115–120. [Google Scholar] [CrossRef]
- Mousivand, A.; Menenti, B.; Gorte, B.; Verhoef, W. Global sensitivity analysis of spectral radiance of a soil-vegetation system. Remote Sens. Environ. 2014, 145, 131–144. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001; p. 339. [Google Scholar]
- Chen, Q. Retrieving vegetation height of forests and woodlands over mountainous areas in the Pacific Coast region using satellite laser altimetry. Remote Sens. Environ. 2010, 114, 1610–1627. [Google Scholar] [CrossRef]
- Natkin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorob. 2013, 7, 1–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cawley, G.C.; Talbot, N.L.C. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Torgo, L.; Ribiero, R.P.; Pfahringer, B.; Branco, P. Smote for regression. In Proceedings of the XVI Portuguese Conference on Artificial Intelligence, Azores, Portugal, 9–12 September 2013; Springer: Berlin, Germany, 2013; pp. 378–389. [Google Scholar]
- Branco, P.; Torgo, L.; Ribiero, R.P. Pre-processing approaches for imbalanced distributions in regression. Neurocomputing 2019, 343, 76–99. [Google Scholar] [CrossRef]
- Bell, D.M.; Gregory, M.J.; Ohmann, J.L. Imputed forest structure uncertainty varies across elevational and longitudinal gradients in the western Cascade Mountains, Oregon, USA. For. Ecol. Manag. 2015, 358, 154–164. [Google Scholar] [CrossRef]
- Heidemann, H.K. Lidar base specification. In U.S. Geological Survey Techniques and Methods, Version 1.3; Chapter B4; US Geological Survey: Reston, VA, USA, 2018; p. 101. [Google Scholar]
- PRISM Climate Group, 2019. Oregon State University. Available online: http://prism.oregonstate.edu (accessed on 9 January 2020).
- McGaughey, R.J. FUSION Version 3.5. USDA Forest Service, Pacific Northwest Research Station, Olympia, WA. Available online: http://forsys.cfr.washington.edu/ (accessed on 9 January 2020).
- Hopkinson, C.; Chasmer, L. Testing LiDAR models of fractional cover across multiple forest ecozones. Remote Sens. Environ. 2009, 113, 275–288. [Google Scholar] [CrossRef]
- Smith, A.M.S.; Falkowski, M.J.; Hudak, A.T.; Evans, J.S.; Robinson, A.P.; Steele, C.M. A cross-comparison of field, spectral, and lidar estimates of forest canopy cover. Can. J. Remote Sens. 2009, 35, 447–459. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Scheel, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the 3rd Earth Resource Technology Satellite Symposium, Washington, DC, USA, 10–14 December 1973; pp. 48–62. [Google Scholar]
- Key, C.H.; Benson, N.C. The Normalized Burn Ratio (NBR): A Landsat TM Radiometric Measure of Burn Severity; US Geological Survey Northern Rocky Mountain Science Center: Bozeman, MT, USA, 2002.
- Crist, E.P. A TM Tasseled Cap equivalent transformation for reflectance factor data. Remote Sens. Environ. 1985, 17, 301–306. [Google Scholar] [CrossRef]
- Huang, C.; Wylie, B.K.; Yang, L.; Homer, C.; Zylstra, G. Derivation of tasseled cap transformation based on Landsat 7 at-satellite reflectance. Int. J. Remote Sens. 2002, 23, 1741–1748. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of tasseled cap transformation based on Landsat 8 at-satellite reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Rollins, M.G.; Ward, B.C.; Dillon, G.; Pratt, S.; Wolf, A. Developing the Landfire Fire Regime Data Products. 2007. Available online: https://landfire.cr.usgs.gov/documents/Developing_the_LANDFIRE_Fire_Regime_Data_Products.pdf (accessed on 9 January 2020).
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geo. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Schmidt, G.L.; Jenkerson, C.B.; Masek, J.G.; Vermote, E.; Gao, F. Landsat Ecosystem Disturbance Adaptive Processing System (LEDAPS) Algorithm Description; Open-File Report No. 2013-1057; US Geological Survey: Reston, VA, USA, 2014; p. 17.
- Egorov, A.V.; Roy, D.P.; Zhang, H.K.; Hansen, M.C.; Kommareddy, A. Demonstration of percent tree cover mapping using analysis ready data (ARD) and sensitivity with respect to Landsat ARD processing level. Remote Sens. 2018, 10, 209. [Google Scholar] [CrossRef] [Green Version]
- Lefsky, M.A.; Cohen, W.B.; Spies, T.A. An evaluation of alternate remote sensing products for forest inventory, monitoring, and mapping of Douglas-fir forests in western Oregon. Can. J. For. Res. 2001, 31, 78–87. [Google Scholar] [CrossRef]
- Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, J.; Venkataraman, S.; Franklin, M.J.; et al. Apache spark: A unified engine for big data processing. Commun. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
- LeDell, E.; Gill, N.; Aiello, S.; Fu, A.; Candel, A.; Click, C.; Kraljevic, T.; Nykodym, T.; Aboyoun, P.; Kurka, M. H2O: R Interface for ‘H2O’. 2019. R Package Version 3.26.02. Available online: https://cran.r-project.org/web/packages/h2o/index.html (accessed on 19 August 2019).
- Luraschi, J.; Kuo, K.; Ushey, K.; Allaire, J.J.; Macedo, S.; RStudio; The Apache Software Foundation. sparklyr: R Interface to Apache Spark. 2019. R Package Version 1.0.2. Available online: https://cran.r-project.org/web/packages/sparklyr/index.html (accessed on 10 August 2019).
- Hava, J.; Gill, N.; LeDell, E.; Malohlava, M.; Allaire, J.J.; RStudio. rsparkling: R Interface for H2O Sparkling Water. 2019. R Package Version 0.2.18. Available online: https://cran.r-project.org/web/packages/rsparkling/index.html (accessed on 10 August 2019).
- Hijmans, R.J.; van Etten, J.; Sumner, M.; Cheng, J.; Bevan, A.; Bivand, R.; Busetto, L.; Canty, M.; Forrest, D.; Ghosh, A. raster: Geographic Data Analysis and Modeling. 2019. R Package Version 2.9-23. Available online: https://cran.r-project.org/web/packages/raster/index.html (accessed on 10 August 2019).
- Wickham, H.; Chang, W.; Henry, L.; Pedersen, T.L.; Takahashi, K.; Wilke, C.; Woo, K.; Yutani, H.; Dunnington, D.; RStudio. ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics. 2019. R Package Version 3.2.1. Available online: https://cran.r-project.org/web/packages/ggplot2/index.html (accessed on 10 August 2019).
- Wickham, H.; François, R.; Henry, L.; Müller, K.; RStudio. dplyr: A Grammar of Data Manipulation. 2019. R Package Version 0.8.3. Available online: https://cran.r-project.org/web/packages/dplyr/index.html (accessed on 10 August 2019).
- H20 Gradient Boosting Machine Documentation. Available online: http://docs.h2o.ai/h2o/latest-stable/h2o-docs/data-science/gbm.html (accessed on 9 January 2019).
- Monitoring Trends in Burn Severity. Available online: https://www.mtbs.gov (accessed on 9 January 2019).
- Picotte, J.J.; Dockter, D.; Long, J.; Tolk, B.; Davidson, A.; Peterson, B. LANDFIRE Remap prototype mapping effort: Developing a new framework for mapping vegetation classification, change, and structure. Fire 2019, 2, 35. [Google Scholar] [CrossRef] [Green Version]
- Keane, R.E.; Reinhardt, E.D.; Scott, J.; Gray, K.; Reardon, J. Estimating forest canopy bulk density using six indirect methods. Can. J. For. Res. 2005, 35, 724–739. [Google Scholar] [CrossRef]
- Reinhardt, E.; Lutes, D.; Scott, J. FuelCalc: A method for estimating fuel characteristics. In Proceedings of the 1st Fire Behavior and Fuels Conference, Portland, OR, USA, 28–30 March 2006; pp. 273–282. [Google Scholar]
- Cruz, M.G.; Alexander, M.E. Assessing crown fire potential in coniferous forests of western North America: A critique of current approaches and recent simulation studies. Int. J. Wildland Fire 2010, 19, 377–398. [Google Scholar] [CrossRef]
- Erdody, T.L.; Moskal, L.M. Fusion of LiDAR and imagery for estimating forest canopy fuels. Remote Sens. Environ. 2010, 114, 725–737. [Google Scholar] [CrossRef]
- Jakubowski, M.K.; Guo, Q.; Kelly, M. Tradeoffs between lidar pulse density and forest measurement accuracy. Remote Sens. Environ. 2013, 130, 245–253. [Google Scholar] [CrossRef]
- Ichii, K.; Kawabata, A.; Yamaguchi, Y. Global correlation analysis for NDVI and climatic variables and NDVI trends: 1982–1990. Int. J. Remote Sens. 2002, 23, 3873–3878. [Google Scholar] [CrossRef]
- Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W. Regional detection, characterization, and attribution of annual forest change from 1984 to 2012 using Landsat-derived time-series metrics. Remote Sens. Environ. 2015, 170, 121–132. [Google Scholar] [CrossRef]
- Roy, D.P.; Zhang, H.K.; Ju, J.; Gomez-Dans, J.L.; Lewis, P.E.; Shaaf, C.B.; Sun, Q.; Li, J.; Huang, H.; Kovalskyy, V. A general method to normalize Landsat reflectance data to nadir BRDF adjusted reflectance. Remote Sens. Environ. 2016, 176, 255–271. [Google Scholar] [CrossRef] [Green Version]
- Pierce, K.B.; Ohmann, J.L.; Wimberly, M.C.; Gregory, M.J.; Fried, J.S. Mapping wildland fuels and forest structure for land management: A comparison of nearest neighbor imputation and other methods. Can. J. For. Res. 2009, 39, 1901–1916. [Google Scholar] [CrossRef]
- Roy, D.P.; Kovalskyy, V.; Zhang, H.K.; Vermote, E.F.; Yan, L.; Kumar, S.S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 reflective wavelength and normalized difference vegetation index continuity. Remote Sens. Environ. 2016, 185, 57–70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Vries, B.; Pratihast, A.K.; Verbesselt, J.; Kooistra, L.; Herold, M. Characterizing forest change using community-based monitoring data and Landsat time series. PLoS ONE 2016, 11, e0147121. [Google Scholar]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Banskota, A.; Kayastha, N.; Falkowski, M.J.; Wulder, M.A.; Froese, R.E.; White, J.C. Forest monitoring using Landsat time series data: A review. Can. J. Rem. Sens. 2014, 40, 362–384. [Google Scholar] [CrossRef]
- Sorenson, R.; Zinko, U.; Seibert, J. On the calculation of the topographic wetness index: Evaluation of different methods based on field observations. Hydrol. Earth Syst. Sci. Discuss. 2006, 10, 101–112. [Google Scholar] [CrossRef] [Green Version]
- Lutz, J.A.; van Wagtendonk, J.W.; Franklin, J.F. Climatic water deficit, tree species ranges, and climate change in Yosemite National Park. J. Biogeogr. 2010, 37, 936–950. [Google Scholar] [CrossRef]
- Mutlu, M.; Popescu, S.C.; Zhao, K. Sensitivity analysis of fire behavior modeling with LIDAR-derived surface fuel maps. For. Ecol. Manag. 2008, 253, 289–294. [Google Scholar] [CrossRef]
- The LANDFIRE Total Fuel Change Tool User’s Guide. Available online: https://www.landfire.gov/documents/LFTFC_Users_Guide.pdf (accessed on 9 January 2020).














| Source | Variable Name | Description | Citations |
|---|---|---|---|
| LiDAR | Canopy Cover (CC) (%) | Percentage of first returns above 2 m | [52,72,73] |
| Canopy Height (CH) (m) | 99th percentile return height | [52] | |
| Canopy Base Height (CBH) (m) | Mean return height minus standard deviation of heights | [52,56] | |
| Canopy Bulk Density (CBD) (kg/m3) | If CH is 0–15 m: stand height class (SH), SH1 = 0 and SH2 = 0 If CH is 15–30 m: SH1 = 1 and SH2 = 0 If CH is 30–91 m: SH1 = 0 and SH2 = 1 If EVT equals Pinyon or Juniper type: PJ = 1 else PJ = 0 | [51] | |
| Landsat | Med NDVI | Median normalized difference vegetation index (NDVI) value | [74] |
| Max NDVI | Maximum NDVI value | [74] | |
| Med NBR | Median normalized burn ratio (NBR) | [75] | |
| Max NBR | Maximum NBR | [75] | |
| Med Bright | Median tasseled cap brightness | [76,77,78] | |
| Max Bright | Maximum tasseled cap brightness | [76,77,78] | |
| Med Green | Median tasseled cap greenness | [76,77,78] | |
| Max Green | Maximum tasseled cap greenness | [76,77,78] | |
| Med Wet | Median tasseled cap wetness | [76,77,78] | |
| Max Wet | Maximum tasseled cap wetness | [76,77,78] | |
| LANDFIRE | EVT | Existing vegetation type | [16] |
| FRG | Fire regime group | [79] | |
| Slope (%) | Slope | ||
| Aspect (deg) | Aspect | ||
| Elev (m) | Elevation | ||
| Lat (deg) | Latitude |
| GBM Model Parameters | Value(s) |
|---|---|
| ntrees | Up to 4000 |
| learn_rate | 0.1 |
| learn_rate_annealing | 0.01 |
| sample_rate | 0.4, 0.6, 0.9, 1 |
| col_sample_rate | 0.6, 0.9, 1 |
| col_sample_rate_per_tree | 0.6, 0.9, 1 |
| col_sample_rate_change_per_level | 0.01, 0.9, 1.1 |
| nbins | 32, 64, 128, 256 |
| min_split_improvement | 0, 1 × 10−4, 1 × 10−6, 1 × 10−8 |
| max_depth | 20, 30, 40 |
| histogram_type | AUTO, UniformAdaptive, QuantilesGlobal |
| stopping_metric | RMSE |
| stopping_tolerance | 0.01 |
| score_tree_interval | 10 |
| stopping_rounds | 3 |
| Metric | CC (%) | CH (m) | CBH (m) | CBD (kg/m3) |
|---|---|---|---|---|
| Local RMSE | 10.02 | 4.91 | 2.33 | 0.057 |
| Global RMSE | 10.10 | 5.31 | 2.50 | 0.059 |
| Local MAE | 7.42 | 3.67 | 1.73 | 0.041 |
| Global MAE | 7.53 | 3.99 | 1.88 | 0.043 |
| Local R² | 0.725 | 0.672 | 0.600 | 0.622 |
| Global R² | 0.729 | 0.631 | 0.547 | 0.602 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moran, C.J.; Kane, V.R.; Seielstad, C.A. Mapping Forest Canopy Fuels in the Western United States with LiDAR–Landsat Covariance. Remote Sens. 2020, 12, 1000. https://doi.org/10.3390/rs12061000
Moran CJ, Kane VR, Seielstad CA. Mapping Forest Canopy Fuels in the Western United States with LiDAR–Landsat Covariance. Remote Sensing. 2020; 12(6):1000. https://doi.org/10.3390/rs12061000
Chicago/Turabian StyleMoran, Christopher J., Van R. Kane, and Carl A. Seielstad. 2020. "Mapping Forest Canopy Fuels in the Western United States with LiDAR–Landsat Covariance" Remote Sensing 12, no. 6: 1000. https://doi.org/10.3390/rs12061000
APA StyleMoran, C. J., Kane, V. R., & Seielstad, C. A. (2020). Mapping Forest Canopy Fuels in the Western United States with LiDAR–Landsat Covariance. Remote Sensing, 12(6), 1000. https://doi.org/10.3390/rs12061000