Effect of X-Ray Tube Configuration on Measurement of Key Soil Fertility Attributes with XRF
Abstract
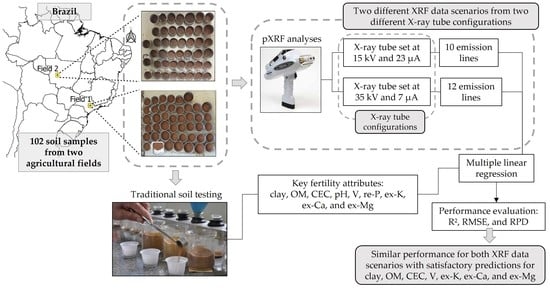
:1. Introduction
2. Materials and Methods
2.1. Study Sites and Soil Samples
2.2. Reference Analyses
2.3. pXRF Measurements with Different Settings
2.4. Modelling
3. Results
3.1. Laboratory Measured Soil Properties
3.2. Effect of X-ray Tube Configuration on XRF Emission Lines
3.3. Effect of X-ray Tube Configuration on pXRF Performance
3.4. pXRF for Key Fertility Attributes Prediction
4. Discussion
4.1. Performance Regarding the X-ray Tube Configuration
4.2. pXRF Models Performance for the Prediction of Key Fertility Attributes
4.3. Perspectives for Using XRF Sensors as a PSS Tool
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A



References
- Molin, J.P.; Tavares, T.R. Sensor systems for mapping soil fertility attributes: Challenges, advances and perspectives in Brazilian tropical soils. Eng. Agric. 2019, 39, 126–147. [Google Scholar] [CrossRef] [Green Version]
- Viscarra Rossel, R.A.; Bouma, J. Soil sensing: A new paradigm for agriculture. Agric. Syst. 2016, 148, 71–74. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.; Adamchuk, V.I.; Sudduth, K.A.; McKenzie, N.J.; Lobsey, C. Proximal soil sensing: An effective approach for soil measurements in space and time. Adv. Agron. 2011, 113, 243–291. [Google Scholar] [CrossRef]
- Kuang, B.; Mahmood, H.S.; Quraishi, M.Z.; Hoogmoed, W.B.; Mouazen, A.M.; van Henten, E.J. Sensing soil properties in the laboratory, in situ, and on-line: A review. Adv. Agron. 2012, 114, 155–223. [Google Scholar] [CrossRef]
- Nawar, S.; Corstanje, R.; Halcro, G.; Mulla, D.; Mouazen, A.M. Delineation of soil management zones for variable-rate fertilization: A review. Adv. Agron. 2017, 143, 175–245. [Google Scholar] [CrossRef]
- Ji, W.; Adamchuk, V.I.; Biswas, A.; Dhawale, N.M.; Sudarsan, B.; Zhang, Y.; Rossel, R.A.; Shi, Z. Assessment of soil properties in situ using a prototype portable MIR spectrometer in two agricultural fields. Biosyst. Eng. 2016, 152, 14–27. [Google Scholar] [CrossRef]
- Archbold, G.; Torres, H.B.; Ruiz, F.; Marín, M.N.; Chaves, D.M.; Arboleda, L.T.; Parra, C.; Carrillo, H.; Mouazen, A.M. pH Measurement IoT System for Precision Agriculture Applications. IEEE Lat. Am. Trans. 2019, 17, 823–832. [Google Scholar] [CrossRef]
- Weindorf, D.C.; Chakraborty, S.; Herrero, J.; Li, B.; Castañeda, C.; Choudhury, A. Simultaneous assessment of key properties of arid soil by combined PXRF and V is–NIR data. Eur. J. Soil Sci. 2016, 67, 173–183. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Zhao, R.; Li, S.; Chen, S.; Jiang, Q.; Zhou, L.; Shi, Z. Multi-sensor fusion for the determination of several soil properties in the Yangtze River Delta, China. Eur. J. Soil Sci. 2019, 70, 162–173. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Hartemink, A.E. Data fusion of vis–NIR and PXRF spectra to predict soil physical and chemical properties. Eur. J. Soil Sci. 2019. [Google Scholar] [CrossRef]
- Tavares, T.R.; Nunes, L.C.; Alves, E.E.N.; Almeida, E.; Maldaner, L.F.; Krug, F.J.; Carvalho, H.W.P.; Molin, J.P. Simplifying sample preparation for soil fertility analysis by X-ray fluorescence spectrometry. Sensors 2019, 19, 5066. [Google Scholar] [CrossRef] [Green Version]
- Weindorf, D.C.; Chakraborty, S. Portable X-ray Fluorescence Spectrometry Analysis of Soils. In Methods of Soil Analysis; Hirmas, D., Madison, W.I., Eds.; Soil Science Society of America: Wisconsin, WI, USA, 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Zhu, Y.; Weindorf, D.C.; Zhang, W. Characterizing soils using a portable X-ray fluorescence spectrometer: 1. Soil texture. Geoderma 2011, 167, 167–177. [Google Scholar] [CrossRef]
- Sharma, A.; Weindorf, D.C.; Man, T.; Aldabaa, A.A.A.; Chakraborty, S. Characterizing soils via portable X-ray fluorescence spectrometer: 3, Soil reaction (pH). Geoderma 2014, 232, 141–147. [Google Scholar] [CrossRef]
- Sharma, A.; Weindorf, D.C.; Wang, D.; Chakraborty, S. Characterizing soils via portable X-ray fluorescence spectrometer: 4, Cation exchange capacity (CEC). Geoderma 2015, 239, 130–134. [Google Scholar] [CrossRef]
- Rawal, A.; Chakraborty, S.; Li, B.; Lewis, K.; Godoy, M.; Paulette, L.; Weindorf, D.C. Determination of base saturation percentage in agricultural soils via portable X-ray fluorescence spectrometer. Geoderma 2019, 338, 375–382. [Google Scholar] [CrossRef]
- Nawar, S.; Delbecque, N.; Declercq, Y.; Smedt, P.; Finke, P.; Verdoodt, A.; Meirvenne, M.V.; Mouazen, A.M. Can spectral analyses improve measurement of key soil fertility parameters with X-ray fluorescence spectrometry? Geoderma 2019, 350, 29–39. [Google Scholar] [CrossRef]
- Towett, E.K.; Shepherd, K.D.; Sila, A.; Aynekulu, E.; Cadisch, G. Mid-infrared and total x-ray fluorescence spectroscopy complementarity for assessment of soil properties. Soil Sci. Soc. Am. J. 2015, 79, 1375–1385. [Google Scholar] [CrossRef] [Green Version]
- Morona, F.; Santos, F.R.; Brinatti, A.M.; Melquiades, F.L. Quick analysis of organic matter in soil by energy-dispersive X-ray fluorescence and multivariate analysis. Appl. Radiat. Isotopes 2017, 130, 13–20. [Google Scholar] [CrossRef]
- Silva, S.H.G.; Teixeira, A.F.D.S.; Menezes, M.D.D.; Guilherme, L.R.G.; Moreira, F.M.D.S.; Curi, N. Multiple linear regression and random forest to predict and map soil properties using data from portable X-ray fluorescence spectrometer (pXRF). Ciênc. Agrotec. 2017, 41, 648–664. [Google Scholar] [CrossRef]
- Andrade, R.; Faria, W.M.; Silva, S.H.G.; Chakraborty, S.; Weindorf, D.C.; Mesquita, L.F.; Guilherme, L.R.G.; Curi, N. Prediction of soil fertility via portable X-ray fluorescence (pXRF) spectrometry and soil texture in the Brazilian Coastal Plains. Geoderma 2020, 357, 113960. [Google Scholar] [CrossRef]
- Teixeira, A.F.D.S.; Weindorf, D.C.; Silva, S.H.G.; Guilherme, L.R.G.; Curi, N. Portable X-ray fluorescence (pXRF) spectrometry applied to the prediction of chemical attributes in Inceptisols under different land uses. Ciênc. Agrotec. 2018, 42, 501–512. [Google Scholar] [CrossRef]
- Santos, F.R.; Oliveira, J.F.; Bona, E.; Santos, J.V.F.; Barboza, G.M.; Melquiades, F.L. EDXRF spectral data combined with PLSR to determine some soil fertility indicators. Microchem. J. 2020, 152, 104275. [Google Scholar] [CrossRef]
- Silva, S.; Poggere, G.; Menezes, M.; Carvalho, G.; Guilherme, L.; Curi, N. Proximal sensing and digital terrain models applied to digital soil mapping and modeling of Brazilian Latosols (Oxisols). Remote Sens. 2016, 8, 614. [Google Scholar] [CrossRef] [Green Version]
- Silva, E.A.; Weindorf, D.C.; Silva, S.H.; Ribeiro, B.T.; Poggere, G.C.; Carvalho, T.S.; Goncalves, M.G.; Guilherme, L.R.; Curi, N. Advances in Tropical Soil Characterization via Portable X-Ray Fluorescence Spectrometry. Pedosphere 2019, 29, 468–482. [Google Scholar] [CrossRef]
- Weindorf, D.C.; Zhu, Y.; Mc Daniel, P.; Valerio, M.; Lynn, L.; Michaelson, G.; Clark, M.; Ping, C.L. Characterizing soils via portable x-ray fluorescence spectrometer: 2. Spodic and Albic horizons. Geoderma 2012, 189, 268–277. [Google Scholar] [CrossRef]
- O’Rourke, S.M.; Stockmann, U.; Holden, N.M.; Mc Bratney, A.B.; Minasny, B. An assessment of model averaging to improve predictive power of portable vis-NIR and XRF for the determination of agronomic soil properties. Geoderma 2016, 279, 31–44. [Google Scholar] [CrossRef]
- Bowers, C. Matrix Effect Corrections in X-ray Fluorescence Spectrometry. J. Chem. Educ. 2019, 96, 2597–2599. [Google Scholar] [CrossRef]
- Jenkins, R. X-Ray Fluorescence Spectrometry; John Wiley & Sons: Hoboken, NJ, USA, 2012; p. 232. [Google Scholar]
- Lindgren, E.S. X-ray fluorescence analysis-energy dispersive. In Encyclopedia of Analytical Chemistry; Meyers, R.A., Ed.; John Wiley & Sons: Chichester, UK, 2000; ISBN 0471-97670-9. [Google Scholar]
- Potts, P.J.; Webb, P.C.; Watson, J.S. Energy-dispersive x-ray fluorescence analysis of silicate rocks for major and trace elements. X-Ray Spectrom. 1984, 13, 2–15. [Google Scholar] [CrossRef]
- Panchuk, V.; Yaroshenko, I.; Legin, A.; Semenov, V.; Kirsanov, D. Application of chemometric methods to XRF-data—A tutorial review. Anal. Chim. Acta 2018, 1040, 19–32. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World reference base for soil resources 2014. In World Soil Resources Reports No. 106; Schad, P., van Huyssteen, C., Micheli, E., Eds.; FAO: Rome, Italy, 2014; p. 189. ISBN 978-92-5-108369-7. [Google Scholar]
- Van Raij, B.; Andrade, J.C.; Cantarela, H.; Quaggio, J.A. Análise Química Para Avaliação de Solos Tropicais; IAC: Campinas, Brazil, 2001; p. 285. (In Portuguese) [Google Scholar]
- Element, C.A.S. Method 3051A microwave assisted acid digestion of sediments, sludges, soils, and oils. Z. Für Anal. Chem. 2007, 111, 362–366. [Google Scholar]
- Silva, Y.J.A.B.; Nascimento, C.W.A.; Biondi, C.M. Comparison of USEPA digestion methods to heavy metals in soil samples. Environ. Monit. Assess. 2014, 186, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Currie, L.A. Limits for qualitative detection and quantitative determination. Application to radiochemistry. Anal. Chem. 1968, 40, 586–593. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Chang, C.W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-infrared reflectance spectroscopy–principal components regression analyses of soil properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef] [Green Version]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Visible and near infrared spectroscopy in soil science. Adv. Agron. 2010, 107, 163–215. [Google Scholar] [CrossRef] [Green Version]
- Mouazen, A.M.; De Baerdemaeker, J.; Ramon, H. Effect of wavelength range on the measurement accuracy of some selected soil constituents using visual-near infrared spectroscopy. J. Near Infrared Spec. 2006, 14, 189–199. [Google Scholar] [CrossRef]
- Van Raij, B. Fertilidade do Solo e Manejo de Nutrientes; International Plant Nutrition Institute (IPNI): Piracicaba, São Paulo, Brazil, 2011; p. 420. (In Portuguese) [Google Scholar]
- Albertini, V.R.; Paci, B.; Generosi, A. Energy dispersive, X-ray fluorescence analysis. In Encyclopedia of Analytical Chemistry: Applications, Theory and Instrumentation; John Wiley & Sons: New York, NY, USA, 2018; pp. 1–17. [Google Scholar] [CrossRef]
- Yılmaz, D.; Boydaş, E. The use of scattering peaks for matrix effect correction in WDXRF analysis. Radiat. Phys. Chem. 2018, 153, 17–20. [Google Scholar] [CrossRef]
- Lima, T.M.; Weindorf, D.C.; Curi, N.; Guilherme, L.R.; Lana, R.M.; Ribeiro, B.T. Elemental analysis of Cerrado agricultural soils via portable X-ray fluorescence spectrometry: Inferences for soil fertility assessment. Geoderma 2019, 353, 264–272. [Google Scholar] [CrossRef]
- Schäefer, C.E.G.R.; Fabris, J.D.; Ker, J.C. Minerals in the clay fraction of Brazilian latosols (oxisols): A review. Clay Miner. 2008, 43, 137–154. [Google Scholar] [CrossRef]
- Singh, B.; Gilkes, R.J. Properties and distribution of iron oxides and their association with minor elements in the soils of south-western Australia. J. Soil Sci. 1992, 43, 77–98. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Lobsey, C. Scoping Review of Proximal Soil Sensors for Grain Growing; CSIRO: Canberra, Australia, 2016. [Google Scholar]
- Fontes, M.P.F. Intemperismo de rochas e minerais. In Pedologia: Fundamentos; Ker, J.C., Curi, N., Schaefer, C.E.G.R., Vidal-Torrado, P., Eds.; Sociedade Brasileira de Ciência do Solo: Viçosa, Brazil, 2012; pp. 181–205. (In Portuguese) [Google Scholar]
- Hartemink, A.E. Soil science in tropical and temperate regions—Some differences and similarities. Adv. Agron. 2002, 77, 269–292. [Google Scholar] [CrossRef]
- Oates, K.M.; Kamprath, E.J. Soil acidity and liming: I. Effect of the extracting solution cation and pH on the removal of aluminum from acid soils. Soil Sci. Soc. Am. J. 1983, 47, 686–689. [Google Scholar] [CrossRef]
- Abreu, C.H., Jr.; Muraoka, T.; Lavorante, A.F. Relationship between acidity and chemical properties of Brazilian soils. Sci. Agric. 2003, 60, 337–343. [Google Scholar] [CrossRef]
- Pavan, M.A.; Bingham, F.T.; Pratt, P.F. Redistribution of Exchangeable Calcium, Magnesium, and Aluminum Following Lime or Gypsum Applications to a Brazilian Oxisol. Soil Sci. Soc. Am. J. 1984, 48, 33–38. [Google Scholar] [CrossRef]
- Büchele, D.; Chao, M.; Ostermann, M.; Leenen, M.; Bald, I. Multivariate chemometrics as a key tool for prediction of K and Fe in a diverse German agricultural soil-set using EDXRF. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef]
- Rodrigues, E.S.; Gomes, M.H.F.; Duran, N.M.; Cassanji, J.G.B.; da Cruz, T.N.M.; Sant’Anna Neto, A.; Savassa, S.M.; de Almeida, E.; Carvalho, H.W.P. Laboratory Microprobe X-Ray Fluorescence in Plant Science: Emerging Applications and Case Studies. Front. Plant Sci. 2018, 9, 1588. [Google Scholar] [CrossRef]
- Bertin, E.P. Introduction to X-ray Spectrometric Analysis; Plenum Press: New York, NY, USA, 1978; p. 485. [Google Scholar]
- Taggart, J.E., Jr.; Lindsay, J.R.; Scott, B.A.; Vivit, D.V.; Bartel, A.J.; Stewart, K.C. Analysis of geologic materials by wavelength-dispersive X-ray fluorescence spectrometry. In Methods for Geochemical Analysis; US Geological Survey Bulletin: Denver, CO, USA, 1987; Volume 1770, pp. E1–E19. [Google Scholar]





| Clay | OM 3 | CEC 4 | pH | V 5 | re-P 6 | ex-K 7 | ex-Ca 7 | ex-Mg 7 | |
|---|---|---|---|---|---|---|---|---|---|
| ----- g dm−3 ----- | mmolc dm−3 | % | mg dm−3 | ------- mmolc dm−3 ------- | |||||
| -------------------------------------------- Calibration set (n = 68) -------------------------------------------- | |||||||||
| Min | 175.00 | 14.00 | 37.50 | 4.60 | 19.00 | 4.00 | 0.90 | 8.00 | 3.00 |
| 1st Qu. | 251.00 | 19.00 | 60.03 | 5.00 | 43.50 | 12.00 | 1.00 | 16.00 | 7.00 |
| Mean | 352.00 | 24.78 | 81.75 | 5.38 | 64.99 | 22.65 | 3.41 | 35.69 | 18.06 |
| 3rd Qu. | 431.00 | 30.75 | 98.58 | 5.78 | 84.00 | 31.5. | 5.68 | 49.75 | 28.00 |
| Max | 511.00 | 37.00 | 148.90 | 6.30 | 92.00 | 104.00 | 10.30 | 78.00 | 54.00 |
| SD 1 | 95.21 | 6.13 | 25.86 | 0.47 | 21.96 | 15.98 | 2.48 | 19.08 | 12.58 |
| CV 2 (%) | 27.05 | 24.72 | 31.63 | 8.67 | 33.80 | 70.55 | 72.73 | 53.44 | 69.65 |
| Skewness | −0.22 | 0.14 | 0.46 | 0.50 | −0.57 | 2.26 | 0.59 | 0.25 | 0.81 |
| Kurtosis | −1.22 | −1.10 | −0.41 | −1.02 | −1.16 | 8.75 | −0.79 | −1.01 | −0.14 |
| -------------------------------------------- Validation set (n = 34) -------------------------------------------- | |||||||||
| Min | 175.00 | 18.00 | 42.50 | 4.70 | 28.00 | 7.00 | 0.90 | 8.00 | 3.00 |
| 1st Qu. | 226.00 | 22.00 | 53.08 | 4.90 | 39.00 | 12.00 | 1.18 | 13.00 | 5.00 |
| Mean | 332.12 | 26.62 | 76.50 | 5.21 | 64.15 | 19.09 | 3.36 | 33.32 | 17.50 |
| 3rd Qu. | 406.25 | 32.00 | 98.90 | 5.50 | 86.25 | 21.00 | 5.50 | 51.25 | 30.00 |
| Max | 463.00 | 35.00 | 138.40 | 6.20 | 91.00 | 59.00 | 7.90 | 75.00 | 47.00 |
| SD1 | 92.03 | 5.48 | 26.14 | 0.37 | 23.42 | 10.65 | 2.26 | 19.71 | 12.81 |
| CV2 (%) | 27.71 | 20.58 | 34.17 | 7.07 | 36.51 | 55.79 | 67.39 | 59.16 | 73.22 |
| Skewness | −0.45 | −0.11 | 0.53 | 0.83 | −0.35 | 2.16 | 0.35 | 0.34 | 0.63 |
| Kurtosis | −1.39 | −1.45 | −0.63 | 0.26 | −1.62 | 5.78 | −1.35 | −1.11 | −0.73 |
| Clay | OM 1 | CEC 2 | pH | V 3 | re-P 4 | ex-K 5 | ex-Ca 5 | ex-Mg 5 | |
|---|---|---|---|---|---|---|---|---|---|
| Clay | 1.00 | 0.59 ** | 0.67 ** | 0.38 ** | 0.81 ** | −0.06 | 0.73 ** | 0.78 ** | 0.64 ** |
| OM | 1.00 | 0.43 ** | −0.01 | 0.62 ** | 0.07 | 0.48 ** | 0.55 ** | 0.44 ** | |
| CEC | 1.00 | 0.42 ** | 0.76 ** | 0.02 | 0.64 ** | 0.93 ** | 0.93 ** | ||
| pH | 1.00 | 0.53 ** | −0.22 * | 0.40 ** | 0.46 ** | 0.44 ** | |||
| V | 1.00 | −0.12 | 0.71 ** | 0.92 ** | 0.84 ** | ||||
| re-P | 1.00 | −0.1 | 0.01 | −0.17 | |||||
| ex-K | 1.00 | 0.68 ** | 0.58 ** | ||||||
| ex-Ca | 1.00 | 0.93 ** | |||||||
| ex-Mg | 1.00 | ||||||||
| Correlation with ptc | 0.11 | 0.90 ** | 0.75 ** | 0.83 ** | |||||
| Clay | OM 1 | CEC 2 | pH | V 3 | re-P 4 | ex-K 5 | ex-Ca 5 | ex-Mg 5 | |
|---|---|---|---|---|---|---|---|---|---|
| -------------------------------------------------------- R2 ---------------------------------------------------------- | |||||||||
| EL-15 | 0.88 | 0.61 | 0.80 | 0.27 | 0.95 | 0.00 | 0.90 | 0.91 | 0.85 |
| EL-35 | 0.91 | 0.72 | 0.75 | 0.38 | 0.96 | 0.03 | 0.90 | 0.91 | 0.83 |
| ------------------------------------------------------ RMSE ------------------------------------------------------- | |||||||||
| EL-15 | 34.7 | 3.55 | 10.42 | 0.36 | 4.83 | 13.86 | 0.71 | 5.74 | 4.88 |
| EL-35 | 31.72 | 2.87 | 11.08 | 0.32 | 4.82 | 13.41 | 0.65 | 5.63 | 4.97 |
| ---------------------------------------------------- RMSE (%) ----------------------------------------------------- | |||||||||
| EL-15 | 12.05 | 20.87 | 10.86 | 24.15 | 7.66 | 26.65 | 10.16 | 8.56 | 11.09 |
| EL-35 | 11.01 | 16.87 | 11.55 | 21.17 | 7.65 | 25.79 | 9.31 | 8.40 | 11.29 |
| ------------------------------------------------------- RPD -------------------------------------------------------- | |||||||||
| EL-15 | 2.65 | 1.54 | 2.51 | 1.02 | 4.85 | 0.77 | 3.18 | 3.44 | 2.63 |
| EL-35 | 2.90 | 1.91 | 2.36 | 1.16 | 4.86 | 0.79 | 3.47 | 3.50 | 2.58 |
| Clay | OM 1 | CEC 2 | pH | V 3 | re-P 4 | ex-K 5 | ex-Ca 5 | ex-Mg 5 | |
|---|---|---|---|---|---|---|---|---|---|
| --------------------------------------------------------- EL-15 --------------------------------------------------------- | |||||||||
| Al-Kα | −1.35 | 1.48 | 0.11 | −1.48 | −0.21 | −1.73 | −2.83 | 0.21 | 1.29 |
| Si-Kα | −2.07 | −0.71 | −0.37 | −0.83 | 2.04 | −0.94 | −2.40 | 2.26 | 2.07 |
| K-Kα | −1.13 | −1.36 | 1.50 | 2.20 | −0.25 | 0.07 | 14.75 | 0.86 | 0.27 |
| Ca-Kα | −0.20 | 1.24 | 5.03 | 2.90 | 7.49 | 1.23 | −5.95 | 9.35 | 7.10 |
| Ti-Kα | −2.31 | −2.54 | 3.58 | 2.05 | −0.46 | −2.55 | 0.01 | 1.55 | 5.41 |
| Mn-Kα | −0.71 | 3.54 | −1.79 | −0.73 | 0.34 | 0.49 | −0.83 | −2.16 | −2.48 |
| Fe-Kα | 9.22 | −0.63 | −0.57 | −0.20 | 2.49 | −0.40 | 1.98 | 2.60 | −1.12 |
| Ni-Kα | −0.09 | −0.26 | −0.05 | 0.03 | 0.59 | 2.81 | 0.37 | 0.41 | −0.80 |
| Cu-Kα | −1.77 | 0.44 | 0.26 | −1.51 | −1.84 | 3.32 | −1.53 | −0.09 | −1.16 |
| Rh-Lα Thomson | 0.52 | 1.97 | 0.23 | −3.22 | 1.97 | 0.20 | −4.06 | 2.28 | 1.73 |
| --------------------------------------------------------- EL-35 --------------------------------------------------------- | |||||||||
| Al-Kα | −1.14 | 0.93 | −0.48 | −0.24 | −0.90 | −0.55 | −1.01 | −1.11 | −0.91 |
| Si-Kα | −2.08 | 0.53 | −0.73 | −1.17 | 0.23 | 0.29 | −0.81 | 0.52 | −0.17 |
| K-Kα | −1.20 | −0.43 | 1.46 | 2.04 | 0.22 | −0.65 | 18.89 | 0.92 | 0.41 |
| Ca-Kα | −0.27 | 1.11 | 4.45 | 3.33 | 7.89 | 1.09 | −5.68 | 9.08 | 5.78 |
| Ti-Kα | −2.99 | −1.91 | 2.73 | 1.30 | −1.61 | −1.61 | −0.93 | 0.09 | 3.54 |
| Mn-Kα | −0.40 | 2.59 | −1.77 | −0.14 | 0.74 | 0.64 | −1.97 | −1.92 | −1.96 |
| Fe-Kα | 5.09 | 0.50 | −0.27 | −1.55 | 0.19 | 0.38 | −1.42 | 0.64 | −0.34 |
| Ni-Kα | −1.12 | −0.73 | 1.26 | −0.07 | 0.09 | 1.44 | −0.49 | 1.13 | 0.75 |
| Cu-Kα | −1.30 | 0.42 | 0.90 | −2.00 | −1.85 | 3.54 | −0.64 | 0.65 | −0.94 |
| Rh-Lα Thomson | −1.07 | 2.32 | −0.88 | −2.40 | 1.02 | 0.27 | −4.27 | 0.65 | −0.50 |
| Rh-Kα Thomson | 0.38 | 0.23 | −0.25 | 0.90 | 1.78 | −1.02 | −1.02 | 1.27 | 0.22 |
| Rh-Kα Compton | −0.61 | 1.07 | −0.43 | −1.83 | −1.79 | 1.13 | −2.38 | −1.46 | −0.63 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tavares, T.R.; Molin, J.P.; Nunes, L.C.; Alves, E.E.N.; Melquiades, F.L.; de Carvalho, H.W.P.; Mouazen, A.M. Effect of X-Ray Tube Configuration on Measurement of Key Soil Fertility Attributes with XRF. Remote Sens. 2020, 12, 963. https://doi.org/10.3390/rs12060963
Tavares TR, Molin JP, Nunes LC, Alves EEN, Melquiades FL, de Carvalho HWP, Mouazen AM. Effect of X-Ray Tube Configuration on Measurement of Key Soil Fertility Attributes with XRF. Remote Sensing. 2020; 12(6):963. https://doi.org/10.3390/rs12060963
Chicago/Turabian StyleTavares, Tiago Rodrigues, José Paulo Molin, Lidiane Cristina Nunes, Elton Eduardo Novais Alves, Fábio L. Melquiades, Hudson Wallace Pereira de Carvalho, and Abdul Mounem Mouazen. 2020. "Effect of X-Ray Tube Configuration on Measurement of Key Soil Fertility Attributes with XRF" Remote Sensing 12, no. 6: 963. https://doi.org/10.3390/rs12060963
APA StyleTavares, T. R., Molin, J. P., Nunes, L. C., Alves, E. E. N., Melquiades, F. L., de Carvalho, H. W. P., & Mouazen, A. M. (2020). Effect of X-Ray Tube Configuration on Measurement of Key Soil Fertility Attributes with XRF. Remote Sensing, 12(6), 963. https://doi.org/10.3390/rs12060963