Signal Extraction from GNSS Position Time Series Using Weighted Wavelet Analysis
Abstract
:1. Introduction
2. Methodologies
2.1. Binary Wavelet Analysis
2.2. Weighted Wavelet Analysis by Considering Formal Errors
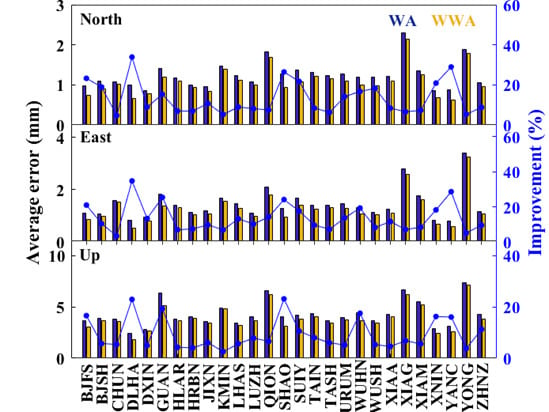
3. Real GNSS Position Time Series Analysis
4. Synthetic Time Series Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Snay, R.A.; Soler, T. Continuously operating reference station (CORS): History, applications, and future enhancements. J. Surv. Eng. 2008, 134, 95–104. [Google Scholar] [CrossRef]
- Uhlemann, M.; Gendt, G.; Ramatschi, M.; Deng, Z. GFZ global multi-GNSS network and data processing results. In IAG 150 Years; Springer: Cham, Switzerland, 2015; pp. 673–679. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhaod, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The multi-GNSS experiment (MGEX) of the international GNSS service (IGS)–achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Tobita, M. Combined logarithmic and exponential function model for fitting postseismic GNSS time series after 2011 Tohoku-Oki earthquake. Earth Planets Space 2016, 68, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Shen, W.; Pan, Y.; Zhang, T. Surface seasonal mass changes and vertical crustal deformation in North China from GPS and GRACE measurements. Geod. Geodyn. 2020, 11, 46–55. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. 2015, 120, 450–487. [Google Scholar] [CrossRef] [Green Version]
- Teferle, F.N.; Bingley, R.M.; Orliac, E.J.; Williams, S.D.P.; Woodworth, P.L.; McLaughlin, D.; Baker, T.F.; Shennan, I.; Milne, G.A.; Bradley, S.L.; et al. Crustal motions in Great Britain: Evidence from continuous GPS, absolute gravity and holocene sea level data. Geophys. J. Int. 2009, 178, 23–46. [Google Scholar] [CrossRef] [Green Version]
- Zou, R.; Freymueller, J.T.; Ding, K.; Yang, S.; Wang, Q. Evaluating seasonal loading models and their impact on global and regional reference frame alignment. J. Geophys. Res. 2014, 119, 1337–1358. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. 2002. [Google Scholar] [CrossRef] [Green Version]
- Rajner, M.; Liwosz, T. Analysis of seasonal position variation for selected GNSS sites in Poland using loading modelling and GRACE data. Geod. Geodyn. 2017, 8, 253–259. [Google Scholar] [CrossRef]
- Yan, J.; Dong, D.; Bürgmann, R.; Materna, K.; Tan, W.; Peng, Y.; Chen, J. Separation of sources of seasonal uplift in China using independent component analysis of GNSS time series. J. Geophys. Res. 2019, 124. [Google Scholar] [CrossRef]
- Bos, M.S.; Bastos, L.; Fernandes, R.M.S. The influence of seasonal signals on the estimation of the tectonic motion in short continuous GPS time-series. J. Geodyn. 2010, 49, 205–209. [Google Scholar] [CrossRef] [Green Version]
- Caporali, A. Average strain rate in the Italian crust inferred from a permanent GPS network–I. Statistical analysis of the time-series of permanent GPS stations. Geophys. J. Int. 2003, 155, 241–253. [Google Scholar] [CrossRef]
- Williams, S.D.P. CATS: GPS coordinate time series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef] [Green Version]
- Langbein, J. Computer algorithm for analyzing and processing borehole strainmeter data. Comput. Geosci. 2010, 36, 611–619. [Google Scholar] [CrossRef]
- Kaczmarek, A.; Kontny, B. Estimates of seasonal signals in GNSS time series and environmental loading models with iterative least-squares estimation (ILSE) approach. Acta. Geodyn. Geomater. 2018, 15, 131–141. [Google Scholar] [CrossRef]
- Klos, A.; Bos, M.S.; Bogusz, J. Detecting time-varying seasonal signal in GPS position time series with different noise levels. GPS Solut. 2018, 22, 21. [Google Scholar] [CrossRef] [Green Version]
- Langbein, J. Noise in GPS displacement measurements from Southern California and Southern Nevada. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Bogusz, J.; Figurski, M. Annual signals observed in regional GPS networks. Acta Geodyn. Geomater. 2014, 11, 125–131. [Google Scholar] [CrossRef] [Green Version]
- Bogusz, J.; Klos, A. On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solut. 2016, 20, 655–664. [Google Scholar] [CrossRef] [Green Version]
- Amiri-Simkooei, A.R.; Tiberius, C.C.J.M.; Teunissen, P.J.G. Assessment of noise in GPS coordinate time series: Methodology and results. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Amiri-Simkooei, A.R.; Mohammadloo, T.H.; Argus, D.F. Multivariate analysis of GPS position time series of JPL second reprocessing campaign. J. Geod. 2017, 91, 685–704. [Google Scholar] [CrossRef] [Green Version]
- Bennett, R.A. Instantaneous deformation from continuous GPS: Contributions from quasi-periodic loads. Geophys. J. Int. 2008, 174, 1052–1064. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; van Dam, T.; Sneeuw, N.; Collilieuxc, X.; Weigeltb, M.; Rebischungc, P. Singular spectrum analysis for modeling seasonal signals from GPS time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Didova, O.; Gunter, B.; Riva, R.; Klees, R.; Roese-Koerner, L. An approach for estimating time-variable rates from geodetic time series. J. Geod. 2016, 90, 1207–1221. [Google Scholar] [CrossRef] [Green Version]
- Ming, F.; Yang, Y.; Zeng, A.; Zhao, B. Decomposition of geodetic time series: A combined simulated annealing algorithm and Kalman filter approach. Adv. Space Res. 2019, 64, 1130–1147. [Google Scholar] [CrossRef]
- Klos, A.; Bos, M.S.; Fernandes, R.M.; Bogusz, J. Noise-dependent adaption of the wiener filter for the GPS position time series. Math. Geosci. 2019, 51, 53–73. [Google Scholar] [CrossRef] [Green Version]
- Morlet, J.; Arens, G.; Fourgeau, E.; Giard, D. Wave propagation and sampling theory—Part I: Complex signal and scattering in multilayered media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef] [Green Version]
- Morlet, J.; Arens, G.; Fourgeau, E.; Giard, D. Wave propagation and sampling theory—Part II: Sampling theory and complex waves. Geophysics 1982, 47, 222–236. [Google Scholar] [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy functions into square integrable wavelets of constant shape. Siam J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Goupillaud, P.; Grossmann, A.; Morlet, J. Cycle-octave and related transforms in seismic signal analysis. Geoexploration 1984, 23, 85–102. [Google Scholar] [CrossRef]
- Liu, L.; Hsu, H.; Grafarend, E.W. Normal morlet wavelet transform and its application to the Earth’s polar motion. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- De Souza, E.M.; Monico, J.F.G. The wavelet method as an alternative for reducing ionospheric effects from single-frequency GPS receivers. J. Geod. 2007, 81, 799–804. [Google Scholar] [CrossRef]
- Martínez, B.; Gilabert, M.A. Vegetation dynamics from NDVI time series analysis using the wavelet transform. Remote Sens. Environ. 2009, 113, 1823–1842. [Google Scholar] [CrossRef]
- Bazine, R.; Wu, H.; Boukhechba, K. Spectral DWT multilevel decomposition with spatial filtering enhancement preprocessing-based approaches for hyperspectral imagery classification. Remote Sens. 2019, 11, 2906. [Google Scholar] [CrossRef] [Green Version]
- Pandey, B.K.; Tiwari, H.; Khare, D. Trend analysis using discrete wavelet transform (DWT) for long-term precipitation (1851–2006) over India. Hydrol. Sci. J. 2017, 62, 2187–2208. [Google Scholar] [CrossRef]
- Wang, D.; Borthwick, A.G.; He, H.; Wang, J.; Zhu, J.; Lu, Y.; Xu, P.; Zeng, X.; Wu, J.; Wang, L.; et al. A hybrid wavelet de-noising and rank-set pair analysis approach for forecasting hydro-meteorological time series. Environ. Res. 2018, 160, 269–281. [Google Scholar] [CrossRef] [Green Version]
- Bracewell, R.; Kahn, P.B. The fourier transform and its applications. Am. J. Phys. 1966, 34, 712. [Google Scholar] [CrossRef]
- Graps, A. An introduction to wavelets. IEEE Comput. Sci. Eng. 1995, 2, 50–61. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Lu, N.; Zhou, J.; Guo, S. An improve gross error detection method for GNSS deformation monitoring time series. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 1282–1288. [Google Scholar]
- Borghi, A.; Cannizzaro, L.; Vitti, A. Advanced techniques for discontinuity detection in GNSS coordinate time-series. An Italian case study. In Geodesy for Planet Earth; Springer: Berlin/Heidelberg, Germany, 2012; pp. 627–634. [Google Scholar]
- Kaczmarek, A.; Kontny, B. Identification of the noise model in the time series of GNSS stations coordinates using wavelet analysis. Remote Sens. 2018, 10, 1611. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Li, K.; Shi, W.; Clarke, K.; Zhang, J.; Li, H. A wavelet-based hybrid approach to remove the flicker noise and the white noise from GPS coordinate time series. GPS Solut. 2015, 19, 511–523. [Google Scholar] [CrossRef]
- Li, Y.; Xu, C.; Yi, L. Denoising effect of multiscale multiway analysis on high-rate GPS observations. GPS Solut. 2017, 21, 31–41. [Google Scholar] [CrossRef]
- Bogusz, J. Geodetic aspects of GPS permanent station non-linearity studies. Acta Geodyn. Geomater. 2015, 12, 180. [Google Scholar] [CrossRef] [Green Version]
- Klos, A.; Bogusz, J.; Bos, M.S. Modelling the GNSS time series: different approaches to extract seasonal signals. In Geodetic Time Series Analysis in Earth Sciences; Springer: Cham, Shwitzerland, 2020; pp. 211–237. [Google Scholar]
- Li, W.; Shen, Y.; Li, B. Weighted spatiotemporal filtering using principal component analysis for analyzing regional GNSS position time series. Acta Geod. Geophys. 2015, 50, 419–436. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Shen, Y. The consideration of formal errors in spatiotemporal filtering using principal component analysis for regional GNSS position time series. Remote Sens. 2018, 10, 534. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Shen, Y.; Li, W.; Chen, Q. Singular spectrum analysis for heterogeneous time series by taking its formal errors into account. Acta Geodyn Geomater. 2018, 4, 395–403. [Google Scholar] [CrossRef]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef] [Green Version]
- Rhif, M.; Ben Abbes, A.; Farah, I.R.; Martinez, B.; Sang, Y. Wavelet transform application for/in non-stationary time-series analysis: A review. Appl. Sci. 2019, 9, 1345. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Tao, B. Practical Methods for Surveying Data Processing; Surveying and Mapping Press: Beijing, China, 2012. [Google Scholar]
- Zhang, S.; Li, Z.; He, Y.; Hou, X.; He, Z.; Wang, Q. Extracting of periodic component of GNSS vertical time series using EMD. Sci. Surv. Mapp. 2018, 43, 80–84. [Google Scholar]
- Langbein, J.; Bock, Y. High-rate real-time GPS network at Parkfield: Utility for detecting fault slip and seismic displacements. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Vitti, A. Sigseg: a tool for the detection of position and velocity discontinuities in geodetic time-series. GPS Solut. 2012, 16, 405–410. [Google Scholar] [CrossRef]
- Shen, Y.; Li, W.; Xu, G.; Li, B. Spatiotemporal filtering of regional GNSS network’s position time series with missing data using principle component analysis. J. Geod. 2014, 88, 1–12. [Google Scholar] [CrossRef]
- Wei, D.; Bovik, A.C.; Evans, B.L. Generalized coiflets: A new family of orthonormal wavelets. In Proceedings of the Conference Record of the Thirty-First Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 1997; IEEE: Piscataway, NJ, USA, 1997. [Google Scholar]
- Scargle, J.D. Studies in astronomical time series analysis. II-Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]













| North | East | Up | |
|---|---|---|---|
| 0.3218 | 0.3192 | 0.3271 | |
| 0.2416 | 0.2372 | 0.2692 | |
| 0.1823 | 0.1898 | 0.2181 | |
| 0.1540 | 0.1463 | 0.1823 | |
| 0.1577 | 0.1380 | 0.1598 | |
| 0.1673 | 0.1616 | 0.1678 | |
| 0.2280 | 0.2284 | 0.2543 | |
| 0.3148 | 0.2797 | 0.4829 | |
| MRMSE | MMAE | |||||
|---|---|---|---|---|---|---|
| WA (mm) | WWA (mm) | IMP (%) | WA (mm) | WWA (mm) | IMP (%) | |
| North | 0.5294 | 0.4770 | 9.90 | 0.4184 | 0.3354 | 19.84 |
| East | 0.3708 | 0.3601 | 2.89 | 0.2543 | 0.2476 | 2.63 |
| Up | 0.9990 | 0.9684 | 3.06 | 0.7180 | 0.6964 | 3.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, K.; Shen, Y.; Wang, F. Signal Extraction from GNSS Position Time Series Using Weighted Wavelet Analysis. Remote Sens. 2020, 12, 992. https://doi.org/10.3390/rs12060992
Ji K, Shen Y, Wang F. Signal Extraction from GNSS Position Time Series Using Weighted Wavelet Analysis. Remote Sensing. 2020; 12(6):992. https://doi.org/10.3390/rs12060992
Chicago/Turabian StyleJi, Kunpu, Yunzhong Shen, and Fengwei Wang. 2020. "Signal Extraction from GNSS Position Time Series Using Weighted Wavelet Analysis" Remote Sensing 12, no. 6: 992. https://doi.org/10.3390/rs12060992
APA StyleJi, K., Shen, Y., & Wang, F. (2020). Signal Extraction from GNSS Position Time Series Using Weighted Wavelet Analysis. Remote Sensing, 12(6), 992. https://doi.org/10.3390/rs12060992