Extrapolating Satellite-Based Flood Masks by One-Class Classification—A Test Case in Houston
Abstract
:1. Introduction
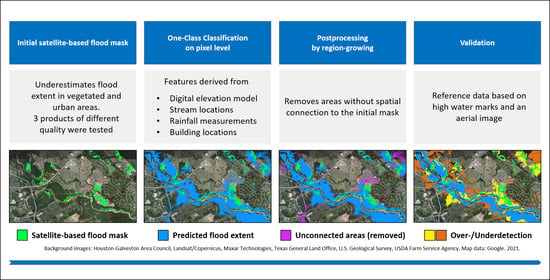
2. Materials & Methods
2.1. Study Area and Datasets
2.1.1. Flood Masks for Training and Validation
2.1.2. Explanatory Features
2.2. Algorithms and Performance Metrics
2.2.1. OCC Algorithms
2.2.2. Post Processing by Region Growing
2.2.3. Performance Metrics
2.3. Experimental Setup
3. Results
3.1. Skill of the Initial Masks
3.2. Skill of the Extrapolation Models
3.3. Spatial Comparison of Predicted Flood Extents
4. Discussion
4.1. Aim and Overall Success
4.2. Features and Algorithms
4.3. Threshold Selection
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Setup ID | Algorithm | Flood Mask | Training Extent | Sampling | Features | -AOI1 | -AOI2 | -AOI3 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | BSVM | EMSR_229 | AOI1 | regular | Topo | 0.977 | 0.59 | 0.47 | 0.54 |
| 1 | MaxEnt | EMSR_229 | AOI1 | regular | Topo | 0.913 | 0.79 | 0.63 | 0.49 |
| 2 | BSVM | EMSR_229 | AOI1 | regular | Topo+Rain | 0.984 | 0.78 | 0.62 | 0.52 |
| 2 | MaxEnt | EMSR_229 | AOI1 | regular | Topo+Rain | 0.942 | 0.78 | 0.62 | 0.56 |
| 3 | BSVM | EMSR_229 | AOI1 | regular | Topo+Buildings | 0.981 | 0.75 | 0.54 | 0.58 |
| 3 | MaxEnt | EMSR_229 | AOI1 | regular | Topo+Buildings | 0.928 | 0.74 | 0.67 | 0.54 |
| 4 | BSVM | EMSR_229 | AOI1 | regular | All | 0.988 | 0.75 | 0.58 | 0.49 |
| 4 | MaxEnt | EMSR_229 | AOI1 | regular | All | 0.946 | 0.73 | 0.64 | 0.58 |
| 5 | BSVM | EMSR_229 | AOI3 | regular | Topo | 0.896 | 0.76 | 0.68 | 0.77 |
| 5 | MaxEnt | EMSR_229 | AOI3 | regular | Topo | 0.848 | 0.79 | 0.6 | 0.75 |
| 6 | BSVM | EMSR_229 | AOI3 | regular | Topo+Rain | 0.911 | 0.75 | 0.69 | 0.76 |
| 6 | MaxEnt | EMSR_229 | AOI3 | regular | Topo+Rain | 0.844 | 0.79 | 0.58 | 0.75 |
| 7 | BSVM | EMSR_229 | AOI3 | regular | Topo+Buildings | 0.917 | 0.86 | 0.73 | 0.77 |
| 7 | MaxEnt | EMSR_229 | AOI3 | regular | Topo+Buildings | 0.872 | 0.89 | 0.76 | 0.78 |
| 8 | BSVM | EMSR_229 | AOI3 | regular | All | 0.927 | 0.84 | 0.69 | 0.76 |
| 8 | MaxEnt | EMSR_229 | AOI3 | regular | All | 0.866 | 0.85 | 0.61 | 0.76 |
| 9 | BSVM | EMSR_229 | Full Extent | regular | Topo | 0.861 | 0.76 | 0.65 | 0.7 |
| 9 | MaxEnt | EMSR_229 | Full Extent | regular | Topo | 0.82 | 0.84 | 0.61 | 0.71 |
| 10 | BSVM | EMSR_229 | Full Extent | regular | Topo+Rain | 0.881 | 0.82 | 0.59 | 0.75 |
| 10 | MaxEnt | EMSR_229 | Full Extent | regular | Topo+Rain | 0.834 | 0.83 | 0.61 | 0.72 |
| 11 | BSVM | EMSR_229 | Full Extent | regular | Topo+Buildings | 0.89 | 0.84 | 0.64 | 0.74 |
| 11 | MaxEnt | EMSR_229 | Full Extent | regular | Topo+Buildings | 0.86 | 0.89 | 0.59 | 0.76 |
| 12 | BSVM | EMSR_229 | Full Extent | regular | All | 0.905 | 0.84 | 0.62 | 0.76 |
| 12 | MaxEnt | EMSR_229 | Full Extent | regular | All | 0.87 | 0.89 | 0.6 | 0.76 |
| 13 | BSVM | EMSR_229 | Full Extent | urban | Topo | 0.85 | 0.77 | 0.67 | 0.7 |
| 13 | MaxEnt | EMSR_229 | Full Extent | urban | Topo | 0.645 | 0.72 | 0.56 | 0.58 |
| 14 | BSVM | EMSR_229 | Full Extent | urban | Topo+Rain | 0.88 | 0.8 | 0.68 | 0.72 |
| 14 | MaxEnt | EMSR_229 | Full Extent | urban | Topo+Rain | 0.664 | 0.74 | 0.58 | 0.59 |
| 15 | BSVM | EMSR_229 | Full Extent | urban | Topo+Buildings | 0.86 | 0.75 | 0.68 | 0.67 |
| 15 | MaxEnt | EMSR_229 | Full Extent | urban | Topo+Buildings | 0.595 | 0.82 | 0.64 | 0.66 |
| 16 | BSVM | EMSR_229 | Full Extent | urban | All | 0.889 | 0.78 | 0.71 | 0.72 |
| 16 | MaxEnt | EMSR_229 | Full Extent | urban | All | 0.599 | 0.82 | 0.64 | 0.66 |
| 17 | BSVM | DLR_BN | AOI1 | regular | Topo | 0.891 | 0.86 | 0.81 | 0.6 |
| 17 | MaxEnt | DLR_BN | AOI1 | regular | Topo | 0.804 | 0.87 | 0.65 | 0.6 |
| 18 | BSVM | DLR_BN | AOI1 | regular | Topo+Rain | 0.904 | 0.83 | 0.81 | 0.54 |
| 18 | MaxEnt | DLR_BN | AOI1 | regular | Topo+Rain | 0.807 | 0.87 | 0.65 | 0.6 |
| 19 | BSVM | DLR_BN | AOI1 | regular | Topo+Buildings | 0.905 | 0.82 | 0.82 | 0.59 |
| 19 | MaxEnt | DLR_BN | AOI1 | regular | Topo+Buildings | 0.809 | 0.86 | 0.64 | 0.61 |
| 20 | BSVM | DLR_BN | AOI1 | regular | All | 0.914 | 0.8 | 0.81 | 0.53 |
| 20 | MaxEnt | DLR_BN | AOI1 | regular | All | 0.812 | 0.86 | 0.64 | 0.61 |
| 21 | BSVM | DLR_BN | AOI1 | urban | Topo | 0.866 | 0.84 | 0.83 | 0.56 |
| 21 | MaxEnt | DLR_BN | AOI1 | urban | Topo | 0.672 | 0.85 | 0.73 | 0.67 |
| 22 | BSVM | DLR_BN | AOI1 | urban | Topo+Rain | 0.882 | 0.81 | 0.82 | 0.52 |
| 22 | MaxEnt | DLR_BN | AOI1 | urban | Topo+Rain | 0.672 | 0.85 | 0.73 | 0.66 |
| 23 | BSVM | DLR_BN | AOI1 | urban | Topo+Buildings | 0.886 | 0.77 | 0.83 | 0.54 |
| 23 | MaxEnt | DLR_BN | AOI1 | urban | Topo+Buildings | 0.538 | 0.87 | 0.64 | 0.69 |
| 24 | BSVM | DLR_BN | AOI1 | urban | All | 0.895 | 0.77 | 0.82 | 0.51 |
| 24 | MaxEnt | DLR_BN | AOI1 | urban | All | 0.539 | 0.87 | 0.64 | 0.68 |
| 25 | BSVM | DLR_CNN | AOI2 | regular | Topo | 0.902 | 0.63 | 0.9 | 0.49 |
| 25 | MaxEnt | DLR_CNN | AOI2 | regular | Topo | 0.876 | 0.65 | 0.94 | 0.63 |
| 26 | BSVM | DLR_CNN | AOI2 | regular | Topo+Rain | 0.904 | 0.62 | 0.91 | 0.47 |
| 26 | MaxEnt | DLR_CNN | AOI2 | regular | Topo+Rain | 0.879 | 0.59 | 0.93 | 0.57 |
| 27 | BSVM | DLR_CNN | AOI2 | regular | Topo+Buildings | 0.904 | 0.81 | 0.91 | 0.5 |
| 27 | MaxEnt | DLR_CNN | AOI2 | regular | Topo+Buildings | 0.876 | 0.88 | 0.94 | 0.72 |
| 28 | BSVM | DLR_CNN | AOI2 | regular | All | 0.906 | 0.62 | 0.94 | 0.55 |
| 28 | MaxEnt | DLR_CNN | AOI2 | regular | All | 0.88 | 0.84 | 0.93 | 0.64 |
| 29 | BSVM | DLR_CNN | AOI2 | urban | Topo | 0.918 | 0.69 | 0.91 | 0.5 |
| 29 | MaxEnt | DLR_CNN | AOI2 | urban | Topo | 0.889 | 0.67 | 0.92 | 0.52 |
| 30 | BSVM | DLR_CNN | AOI2 | urban | Topo+Rain | 0.923 | 0.58 | 0.91 | 0.53 |
| 30 | MaxEnt | DLR_CNN | AOI2 | urban | Topo+Rain | 0.901 | 0.68 | 0.93 | 0.56 |
| 31 | BSVM | DLR_CNN | AOI2 | urban | Topo+Buildings | 0.926 | 0.49 | 0.88 | 0.5 |
| 31 | MaxEnt | DLR_CNN | AOI2 | urban | Topo+Buildings | 0.9 | 0.72 | 0.9 | 0.6 |
| 32 | BSVM | DLR_CNN | AOI2 | urban | All | 0.931 | 0.58 | 0.91 | 0.44 |
| 32 | MaxEnt | DLR_CNN | AOI2 | urban | All | 0.909 | 0.71 | 0.91 | 0.63 |
| 33 | SVM | NOAA_labeled | AOI1 | regular | Topo | 0.966 | 0.97 | 0.92 | 0.63 |
| 34 | SVM | NOAA_labeled | AOI1 | regular | Topo+Rain | 0.971 | 0.97 | 0.93 | 0.6 |
| 35 | SVM | NOAA_labeled | AOI1 | regular | Topo+Buildings | 0.970 | 0.97 | 0.93 | 0.64 |
| 36 | SVM | NOAA_labeled | AOI1 | regular | All | 0.973 | 0.98 | 0.94 | 0.62 |
| 37 | SVM | NOAA_labeled | AOI2 | regular | Topo | 0.976 | 0.57 | 0.98 | 0.54 |
| 38 | SVM | NOAA_labeled | AOI2 | regular | Topo+Rain | 0.980 | 0.57 | 0.98 | 0.49 |
| 39 | SVM | NOAA_labeled | AOI2 | regular | Topo+Buildings | 0.978 | 0.59 | 0.98 | 0.47 |
| 40 | SVM | NOAA_labeled | AOI2 | regular | All | 0.982 | 0.62 | 0.98 | 0.43 |
| 41 | SVM | USGS_SJ | AOI3 | regular | Topo | 0.912 | 0.84 | 0.66 | 0.92 |
| 42 | SVM | USGS_SJ | AOI3 | regular | Topo+Rain | 0.925 | 0.85 | 0.68 | 0.94 |
| 43 | SVM | USGS_SJ | AOI3 | regular | Topo+Buildings | 0.923 | 0.86 | 0.67 | 0.93 |
| 44 | SVM | USGS_SJ | AOI3 | regular | All | 0.934 | 0.85 | 0.7 | 0.94 |
References
- Hostache, R.; Chini, M.; Giustarini, L.; Neal, J.; Kavetski, D.; Wood, M.; Corato, G.; Pelich, R.M.; Matgen, P. Near-Real-Time Assimilation of SAR-Derived Flood Maps for Improving Flood Forecasts. Water Resour. Res. 2018, 54, 5516–5535. [Google Scholar] [CrossRef]
- Mason, D.; Speck, R.; Devereux, B.; Schumann, G.P.; Neal, J.; Bates, P. Flood Detection in Urban Areas Using TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2010, 48, 882–894. [Google Scholar] [CrossRef] [Green Version]
- Pulvirenti, L.; Chini, M.; Pierdicca, N.; Boni, G. Use of SAR Data for Detecting Floodwater in Urban and Agricultural Areas: The Role of the Interferometric Coherence. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1532–1544. [Google Scholar] [CrossRef]
- Sieg, T.; Vogel, K.; Merz, B.; Kreibich, H. Seamless Estimation of Hydrometeorological Risk Across Spatial Scales. Earth’s Future 2019. [Google Scholar] [CrossRef] [Green Version]
- Henderson, F.M.; Lewis, A.J. Radar detection of wetland ecosystems: A review. Int. J. Remote Sens. 2008, 29, 5809–5835. [Google Scholar] [CrossRef]
- Plank, S.; Jüssi, M.; Martinis, S.; Twele, A. Mapping of flooded vegetation by means of polarimetric Sentinel-1 and ALOS-2/PALSAR-2 imagery. Int. J. Remote Sens. 2017, 38, 3831–3850. [Google Scholar] [CrossRef]
- Zwenzner, H.; Voigt, S. Improved estimation of flood parameters by combining space based SAR data with very high resolution digital elevation data. Hydrol. Earth Syst. Sci. Discuss. 2008, 5, 2951–2973. [Google Scholar] [CrossRef]
- Cian, F.; Marconcini, M.; Ceccato, P.; Giupponi, C. Flood depth estimation by means of high-resolution SAR images and lidar data. Nat. Hazards Earth Syst. Sci. 2018, 18, 3063–3084. [Google Scholar] [CrossRef] [Green Version]
- Cohen, S.; Brakenridge, G.R.; Kettner, A.; Bates, B.; Nelson, J.; McDonald, R.; Huang, Y.F.; Munasinghe, D.; Zhang, J. Estimating Floodwater Depths from Flood Inundation Maps and Topography. JAWRA J. Am. Water Resour. Assoc. 2017, 54, 847–858. [Google Scholar] [CrossRef]
- Matgen, P.; Giustarini, L.; Chini, M.; Hostache, R.; Wood, M.; Schlaffer, S. Creating a water depth map from SAR flood extent and topography data. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–16 July 2016. [Google Scholar] [CrossRef]
- Schumann, G.; Pappenberger, F.; Matgen, P. Estimating uncertainty associated with water stages from a single SAR image. Adv. Water Resour. 2008, 31, 1038–1047. [Google Scholar] [CrossRef]
- Stephens, E.; Bates, P.; Freer, J.; Mason, D. The impact of uncertainty in satellite data on the assessment of flood inundation models. J. Hydrol. 2012, 414–415, 162–173. [Google Scholar] [CrossRef] [Green Version]
- Giustarini, L.; Vernieuwe, H.; Verwaeren, J.; Chini, M.; Hostache, R.; Matgen, P.; Verhoest, N.; Baets, B.D. Accounting for image uncertainty in SAR-based flood mapping. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 70–77. [Google Scholar] [CrossRef]
- Martinis, S.; Rieke, C. Backscatter Analysis Using Multi-Temporal and Multi-Frequency SAR Data in the Context of Flood Mapping at River Saale, Germany. Remote Sens. 2015, 7, 7732–7752. [Google Scholar] [CrossRef] [Green Version]
- Martinis, S.; Twele, A.; Voigt, S. Towards operational near real-time flood detection using a split-based automatic thresholding procedure on high resolution TerraSAR-X data. Nat. Hazards Earth Syst. Sci. 2009, 9, 303–314. [Google Scholar] [CrossRef]
- Horritt, M.S.; Mason, D.C.; Luckman, A.J. Flood boundary delineation from Synthetic Aperture Radar imagery using a statistical active contour model. Int. J. Remote Sens. 2001, 22, 2489–2507. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Pierdicca, N.; Chini, M.; Guerriero, L. An algorithm for operational flood mapping from Synthetic Aperture Radar (SAR) data using fuzzy logic. Nat. Hazards Earth Syst. Sci. 2011, 11, 529–540. [Google Scholar] [CrossRef] [Green Version]
- Twele, A.; Cao, W.; Plank, S.; Martinis, S. Sentinel-1-based flood mapping: A fully automated processing chain. Int. J. Remote Sens. 2016, 37, 2990–3004. [Google Scholar] [CrossRef]
- Schlaffer, S.; Matgen, P.; Hollaus, M.; Wagner, W. Flood detection from multi-temporal SAR data using harmonic analysis and change detection. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 15–24. [Google Scholar] [CrossRef]
- Li, Y.; Martinis, S.; Wieland, M.; Schlaffer, S.; Natsuaki, R. Urban Flood Mapping Using SAR Intensity and Interferometric Coherence via Bayesian Network Fusion. Remote Sens. 2019, 11, 2231. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Martinis, S.; Wieland, M. Urban flood mapping with an active self-learning convolutional neural network based on TerraSAR-X intensity and interferometric coherence. ISPRS J. Photogramm. Remote Sens. 2019, 152, 178–191. [Google Scholar] [CrossRef]
- Bonafilia, D.; Tellman, B.; Anderson, T.; Issenberg, E. Sen1Floods11: A georeferenced dataset to train and test deep learning flood algorithms for Sentinel-1. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020. [Google Scholar] [CrossRef]
- Chini, M.; Pelich, R.; Pulvirenti, L.; Pierdicca, N.; Hostache, R.; Matgen, P. Sentinel-1 InSAR Coherence to Detect Floodwater in Urban Areas: Houston and Hurricane Harvey as A Test Case. Remote Sens. 2019, 11, 107. [Google Scholar] [CrossRef] [Green Version]
- Wieland, M.; Martinis, S. A Modular Processing Chain for Automated Flood Monitoring from Multi-Spectral Satellite Data. Remote Sens. 2019, 11, 2330. [Google Scholar] [CrossRef] [Green Version]
- Mason, D.; Schumann, G.P.; Neal, J.; Garcia-Pintado, J.; Bates, P. Automatic near real-time selection of flood water levels from high resolution Synthetic Aperture Radar images for assimilation into hydraulic models: A case study. Remote Sens. Environ. 2012, 124, 705–716. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Nguyen, B.D.; Zhang, S.; Cao, S.; Wagner, W. A Comparison of Terrain Indices toward Their Ability in Assisting Surface Water Mapping from Sentinel-1 Data. ISPRS Int. J. Geo-Inf. 2017, 6, 140. [Google Scholar] [CrossRef] [Green Version]
- Scotti, V.; Giannini, M.; Cioffi, F. Enhanced flood mapping using synthetic aperture radar (SAR) images, hydraulic modelling, and social media: A case study of Hurricane Harvey (Houston, TX). J. Flood Risk Manag. 2020. [Google Scholar] [CrossRef]
- Martinis, S. A Sentinel-1 Times Series-Based Exclusion Layer for Improved Flood Mapping in Arid Areas. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- Samela, C.; Troy, T.J.; Manfreda, S. Geomorphic classifiers for flood-prone areas delineation for data-scarce environments. Adv. Water Resour. 2017, 102, 13–28. [Google Scholar] [CrossRef]
- Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Bui, D.T.; Pham, B.T.; Khosravi, K. A novel hybrid artificial intelligence approach for flood susceptibility assessment. Environ. Model. Softw. 2017, 95, 229–245. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Kumar, L.; Jebur, M.N.; Shabani, F. Evaluating the application of the statistical index method in flood susceptibility mapping and its comparison with frequency ratio and logistic regression methods. Geomat. Nat. Hazards Risk 2018, 10, 79–101. [Google Scholar] [CrossRef]
- Kelleher, C.; McPhillips, L. Exploring the application of topographic indices in urban areas as indicators of pluvial flooding locations. Hydrol. Process. 2019, 34, 780–794. [Google Scholar] [CrossRef]
- Mukherjee, F.; Singh, D. Detecting flood prone areas in Harris County: A GIS based analysis. GeoJournal 2019, 85, 647–663. [Google Scholar] [CrossRef]
- Rennó, C.D.; Nobre, A.D.; Cuartas, L.A.; Soares, J.V.; Hodnett, M.G.; Tomasella, J.; Waterloo, M.J. HAND, a new terrain descriptor using SRTM-DEM: Mapping terra-firme rainforest environments in Amazonia. Remote Sens. Environ. 2008, 112, 3469–3481. [Google Scholar] [CrossRef]
- Quinn, P.; Beven, K.; Chevallier, P.; Planchon, O. The prediction of hillslope flow paths for distributed hydrological modelling using digital terrain models. Hydrol. Process. 1991, 5, 59–79. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef] [Green Version]
- Mack, B.; Roscher, R.; Stenzel, S.; Feilhauer, H.; Schmidtlein, S.; Waske, B. Mapping raised bogs with an iterative one-class classification approach. ISPRS J. Photogramm. Remote Sens. 2016, 120, 53–64. [Google Scholar] [CrossRef]
- Piiroinen, R.; Fassnacht, F.E.; Heiskanen, J.; Maeda, E.; Mack, B.; Pellikka, P. Invasive tree species detection in the Eastern Arc Mountains biodiversity hotspot using one class classification. Remote Sens. Environ. 2018, 218, 119–131. [Google Scholar] [CrossRef]
- Ortiz, S.; Breidenbach, J.; Kändler, G. Early Detection of Bark Beetle Green Attack Using TerraSAR-X and RapidEye Data. Remote Sens. 2013, 5, 1912–1931. [Google Scholar] [CrossRef] [Green Version]
- Jozani, H.J.; Thiel, M.; Abdel-Rahman, E.M.; Richard, K.; Landmann, T.; Subramanian, S.; Hahn, M. Investigation of Maize Lethal Necrosis (MLN) severity and cropping systems mapping in agro-ecological maize systems in Bomet, Kenya utilizing RapidEye and Landsat-8 Imagery. Geol. Ecol. Landsc. 2020, 1–16. [Google Scholar] [CrossRef]
- Mack, B.; Waske, B. In-depth comparisons of MaxEnt, biased SVM and one-class SVM for one-class classification of remote sensing data. Remote Sens. Lett. 2016, 8, 290–299. [Google Scholar] [CrossRef]
- Liu, B.; Dai, Y.; Li, X.; Lee, W.; Yu, P. Building text classifiers using positive and unlabeled examples. In Proceedings of the Third IEEE International Conference on Data Mining, Melbourne, FL, USA, 22 November 2003. [Google Scholar] [CrossRef]
- NHC. Costliest U.S. Tropical Cyclones Tables Updated; Technical Report; National Hurricane Center: Miami, FL, USA, 2018.
- Wing, O.E.; Sampson, C.C.; Bates, P.D.; Quinn, N.; Smith, A.M.; Neal, J.C. A flood inundation forecast of Hurricane Harvey using a continental-scale 2D hydrodynamic model. J. Hydrol. X 2019, 4, 100039. [Google Scholar] [CrossRef]
- Lindner, J.; Fitzgerald, S. Hurricane Harvey—Storm and Flood Information; Technical Report; Harris County Flood Control District (HCFCD): Houston, TX, USA, 2018. [Google Scholar]
- HCFCD. Hurricane Harvey: Impact and Response in Harris County; Technical Report; Harris County Flood Control District: Houston, TX, USA, 2018. [Google Scholar]
- Watson, K.M.; Harwell, G.R.; Wallace, D.S.; Welborn, T.L.; Stengel, V.G.; McDowell, J.S. Characterization of Peak Streamflows and Flood Inundation of Selected Areas in Southeastern Texas and southwestern Louisiana from the August and September 2017 Flood Resulting from Hurricane Harvey; U.S. Geological Survey: Austin, TX, USA, 2018. [CrossRef]
- Arundel, S.; Phillips, L.; Lowe, A.; Bobinmyer, J.; Mantey, K.; Dunn, C.; Constance, E.; Usery, E. PreparingThe National Mapfor the 3D Elevation Program—Products, process and research. Cartogr. Geogr. Inf. Sci. 2015, 42, 40–53. [Google Scholar] [CrossRef]
- Reu, J.D.; Bourgeois, J.; Bats, M.; Zwertvaegher, A.; Gelorini, V.; Smedt, P.D.; Chu, W.; Antrop, M.; Maeyer, P.D.; Finke, P.; et al. Application of the topographic position index to heterogeneous landscapes. Geomorphology 2013, 186, 39–49. [Google Scholar] [CrossRef]
- Evans, J.S. spatialEco. 2021. R Package Version 1.3-6. Available online: https://github.com/jeffreyevans/spatialEco (accessed on 21 May 2021).
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Dudík, M.; Schapire, R.E.; Blair, M.E. Opening the black box: An open-source release of Maxent. Ecography 2017, 40, 887–893. [Google Scholar] [CrossRef]
- Elith, J.; Phillips, S.J.; Hastie, T.; Dudík, M.; Chee, Y.E.; Yates, C.J. A statistical explanation of MaxEnt for ecologists. Divers. Distrib. 2010, 17, 43–57. [Google Scholar] [CrossRef]
- Guillera-Arroita, G.; Lahoz-Monfort, J.J.; Elith, J. Maxent is not a presence-absence method: A comment on Thibaudet al. Methods Ecol. Evol. 2014, 5, 1192–1197. [Google Scholar] [CrossRef]
- Merow, C.; Smith, M.J.; Silander, J.A. A practical guide to MaxEnt for modeling species’ distributions: What it does, and why inputs and settings matter. Ecography 2013, 36, 1058–1069. [Google Scholar] [CrossRef]
- Lowekamp, B.C.; Chen, D.T.; Ibáñez, L.; Blezek, D. The Design of SimpleITK. Front. Neuroinformatics 2013, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, W.S.; Liu, B. Learning with Positive and Unlabeled Examples Using Weighted Logistic Regression. In Proceedings of the Twentieth International Conference on Machine Learning (ICML-2003), Washington, DC, USA, 21–24 August 2003; Volume 20, pp. 448–455. [Google Scholar]
- Mack, B.; Roscher, R.; Waske, B. Can I Trust My One-Class Classification? Remote Sens. 2014, 6, 8779–8802. [Google Scholar] [CrossRef] [Green Version]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Giustarini, L.; Hostache, R.; Matgen, P.; Schumann, G.J.P.; Bates, P.D.; Mason, D.C. A Change Detection Approach to Flood Mapping in Urban Areas Using TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2417–2430. [Google Scholar] [CrossRef] [Green Version]
- Matgen, P.; Hostache, R.; Schumann, G.; Pfister, L.; Hoffmann, L.; Savenije, H. Towards an automated SAR-based flood monitoring system: Lessons learned from two case studies. Phys. Chem. Earth Parts A/B/C 2011, 36, 241–252. [Google Scholar] [CrossRef]
- Jalayer, F.; Risi, R.D.; Paola, F.D.; Giugni, M.; Manfredi, G.; Gasparini, P.; Topa, M.E.; Yonas, N.; Yeshitela, K.; Nebebe, A.; et al. Probabilistic GIS-based method for delineation of urban flooding risk hotspots. Nat. Hazards 2014. [Google Scholar] [CrossRef]
- Yu, L.; Wang, Z.; Tian, S.; Ye, F.; Ding, J.; Kong, J. Convolutional Neural Networks for Water Body Extraction from Landsat Imagery. Int. J. Comput. Intell. Appl. 2017, 16, 1750001. [Google Scholar] [CrossRef]
- Wu, G.; Guo, Y.; Song, X.; Guo, Z.; Zhang, H.; Shi, X.; Shibasaki, R.; Shao, X. A Stacked Fully Convolutional Networks with Feature Alignment Framework for Multi-Label Land-cover Segmentation. Remote Sens. 2019, 11, 1051. [Google Scholar] [CrossRef] [Green Version]
- Ng, A.Y.; Jordan, M.I. On Discriminative vs. Generative Classifiers: A comparison of logistic regression and naive Bayes. In Advances in Neural Information Processing Systems 14; Dietterich, T.G., Becker, S., Ghahramani, Z., Eds.; MIT Press: Cambridge, MA, USA, 2002; pp. 841–848. [Google Scholar]
- Weiss, G.M.; Provost, F. The effect of class distribution on classifier learning: An empirical study. Rutgers Univ. 2001. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Elkan, C. A Positive and Unlabeled Learning Algorithm for One-Class Classification of Remote-Sensing Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 717–725. [Google Scholar] [CrossRef]
- Ruff, L.; Vandermeulen, R.; Goernitz, N.; Deecke, L.; Siddiqui, S.A.; Binder, A.; Müller, E.; Kloft, M. Deep One-Class Classification. In Proceedings of Machine Learning Research, Proceedings of the 35th International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; Rutgers University: New Brunswick, NJ, USA, 2018; Volume 80, pp. 4393–4402. [Google Scholar]
- Phillips, S.J.; Dudík, M. Modeling of species distributions with Maxent: New extensions and a comprehensive evaluation. Ecography 2008, 31, 161–175. [Google Scholar] [CrossRef]









| Floodmask | Data Source | Date of Image | Resolution | Usage |
|---|---|---|---|---|
| EMSR_229 | Cosmo-SkyMed | 31 August 2017 | 30 m | Training |
| DLR_BN | Sentinel-1 | 30 August 2017 | 15 m | Training |
| DLR_CNN | TerraSAR-X | 1 September 2017 | 40 m (32 × 1.25) | Training |
| NOAA_labeled | Aerial image | 30 August 2017 | 0.5 m | Validation |
| USGS_SJ | HWM | Maximum extent | 3 m | Validation |
| Feature | Data Source | Category |
|---|---|---|
| HAND_large_lake_river | NED + OSM | Topo |
| HAND_major_river | NED + OSM | Topo |
| HAND_small_stream_canal | NED + OSM | Topo |
| Dist_large_lake_river | OSM | Topo |
| Dist_major_river | OSM | Topo |
| Dist_small_stream_canal | OSM | Topo |
| Slope | NED | Topo |
| Curvature | NED | Topo |
| TWI | NED | Topo |
| TPI 11x11 | NED | Topo |
| TPI 51x51 | NED | Topo |
| TPI 101x101 | NED | Topo |
| Rainfall_sum | NWS | Rain |
| Rainfall_acc | NWS + NED | Rain |
| Dist_to_buildings | Microsoft USBuildingFootprints | Buildings |
| Product—AOI | %open | %veg. | %urban | EB | Sens. | Spec. | Acc. | |||
|---|---|---|---|---|---|---|---|---|---|---|
| EMSR_229 - 1/West Houston | 32.06 | 1.16 | 0.43 | 0.001 | 0.06 | 0.999 | 0.63 | 0.07 | 0.01 | 0.01 |
| EMSR_229 - 2/Buffalo Bayou | 0 | 1.16 | 0 | - | 0 | 0 | 0 | 0 | 0 | 0 |
| EMSR_229 - 3/San Jacinto | - | - | - | 0.01 | 0.05 | 0.99 | 0.76 | 0.06 | - | - |
| DLR_BN - 1/West Houston | 69.01 | 19.60 | 41.36 | 0.03 | 0.32 | 0.99 | 0.73 | 0.34 | 0.24 | 0.51 |
| DLR_BN - 2/Buffalo Bayou | 3.53 | 6.93 | 23.27 | 0.04 | 0.21 | 0.99 | 0.82 | 0.28 | 0.06 | 0.31 |
| DLR_CNN - 2/Buffalo Bayou | 63.77 | 46.84 | 42.41 | 0.13 | 0.44 | 0.98 | 0.86 | 0.51 | 0.27 | 0.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brill, F.; Schlaffer, S.; Martinis, S.; Schröter, K.; Kreibich, H. Extrapolating Satellite-Based Flood Masks by One-Class Classification—A Test Case in Houston. Remote Sens. 2021, 13, 2042. https://doi.org/10.3390/rs13112042
Brill F, Schlaffer S, Martinis S, Schröter K, Kreibich H. Extrapolating Satellite-Based Flood Masks by One-Class Classification—A Test Case in Houston. Remote Sensing. 2021; 13(11):2042. https://doi.org/10.3390/rs13112042
Chicago/Turabian StyleBrill, Fabio, Stefan Schlaffer, Sandro Martinis, Kai Schröter, and Heidi Kreibich. 2021. "Extrapolating Satellite-Based Flood Masks by One-Class Classification—A Test Case in Houston" Remote Sensing 13, no. 11: 2042. https://doi.org/10.3390/rs13112042
APA StyleBrill, F., Schlaffer, S., Martinis, S., Schröter, K., & Kreibich, H. (2021). Extrapolating Satellite-Based Flood Masks by One-Class Classification—A Test Case in Houston. Remote Sensing, 13(11), 2042. https://doi.org/10.3390/rs13112042