Next Article in Journal
Impact of Atmospheric Optical Properties on Net Ecosystem Productivity of Peatland in Poland
Next Article in Special Issue
Recommendations for HCHO and SO2 Retrieval Settings from MAX-DOAS Observations under Different Meteorological Conditions
Previous Article in Journal
Spatial and Temporal Variability of Minimum Brightness Temperature at the 6.925 GHz Band of AMSR2 for the Arctic and Antarctic Oceans
Previous Article in Special Issue
WRF-Chem Simulation for Modeling Seasonal Variations and Distributions of Aerosol Pollutants over the Middle East
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 11
10.3390/rs13112121
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Technical Note

Hourly Ground-Level PM2.5 Estimation Using Geostationary Satellite and Reanalysis Data via Deep Learning

by
Changsuk Lee
1,†,
Kyunghwa Lee
1,
Sangmin Kim
1,
Jinhyeok Yu
2,
Seungtaek Jeong
3,† and
Jongmin Yeom
3,*
1
Environmental Satellite Center, Climate and Air Quality Research Department, National Institute of Environmental Research, Incheon 22689, Korea
2
School of Earth Sciences and Environmental Engineering, Gwangju Institute of Science and Technology (GIST), Gwangju 61005, Korea
3
Korea Aerospace Research Institute, 169-84 Gwahak-ro, Yuseong-gu, Daejeon 305-806, Korea
*
Author to whom correspondence should be addressed.
†
Equal contribution to the leading authorship goes to this author.
Remote Sens. 2021, 13(11), 2121; https://doi.org/10.3390/rs13112121
Submission received: 28 April 2021 / Revised: 25 May 2021 / Accepted: 26 May 2021 / Published: 28 May 2021
(This article belongs to the Special Issue Remote Sensing of Atmospheric Aerosols over Asia: Methods and Applications)
Browse Figures
Versions Notes

Abstract

:
This study proposes an improved approach for monitoring the spatial concentrations of hourly particulate matter less than 2.5 μm in diameter (PM2.5) via a deep neural network (DNN) using geostationary ocean color imager (GOCI) images and unified model (UM) reanalysis data over the Korean Peninsula. The DNN performance was optimized to determine the appropriate training model structures, incorporating hyperparameter tuning, regularization, early stopping, and input and output variable normalization to prevent training dataset overfitting. Near-surface atmospheric information from the UM was also used as an input variable to spatially generalize the DNN model. The retrieved PM2.5 from the DNN was compared with estimates from random forest, multiple linear regression, and the Community Multiscale Air Quality model. The DNN demonstrated the highest accuracy compared to that of the conventional methods for the hold-out validation (root mean square error (RMSE) = 7.042 μg/m3, mean bias error (MBE) = −0.340 μg/m3, and coefficient of determination (R2) = 0.698) and the cross-validation (RMSE = 9.166 μg/m3, MBE = 0.293 μg/m3, and R2 = 0.49). Although the R2 was low due to underestimated high PM2.5 concentration patterns, the RMSE and MBE demonstrated reliable accuracy values (<10 μg/m3 and 1 μg/m3, respectively) for the hold-out validation and cross-validation.

Graphical Abstract

1. Introduction

Airborne particulate matter (PM) consists of solid particles, liquid droplets, or a mixture of both suspended in the air. PM with aerodynamic diameters of less than 2.5 μm (PM2.5) and 10 μm (PM10) are two of the most widespread health threats, causing respiratory disease due to their penetration into the skin, lungs, and bronchi [1,2,3]. In addition to its effect on health, PM diminishes visibility and affects the climate both directly and indirectly by influencing the global radiation budget [4,5]. Therefore, monitoring PM10 and PM2.5 exposure is necessary to accurately diagnose air quality, address public health risks, and understand the climate effects of ground-level aerosols. One challenge for the aforementioned studies is a lack of accurate spatial and temporal distributions of ground-level PM2.5 [6,7].
To support the assessment of PM exposure, ground stationary observations have been conducted to monitor ground-level air quality. Although the ground-based monitoring has provided reliable and accurate measurements with high temporal resolutions, there is a major limitation in capturing spatially continuous variations in PM, even though there are dense distributions of observation sites. It is difficult to ensure the homogeneity of the observed location, and even instruments of the same model may have various mechanical errors, making them unsuitable to obtain spatially continuous data. Recently, satellites have become a promising tool for studying the dynamics of aerosol optical properties due to their broad coverage and multispectral bands [8]. In particular, satellite-based aerosol optical depth (AOD) has been widely used to estimate the spatial and temporal distributions of PM2.5 at ground level, and it has demonstrated effective performance in regions where ground measurements are limited [9,10].
From the spatial retrieval methodology perspective, most traditional studies are roughly divided into four categories, namely multiple linear regression (MLR [11]), mixed-effect model (MEM [12]), geographically weighted regression (GWR [13]), and chemical-transport model (CTM), to estimate or predict ground-level PM2.5 using satellite-based AOD, according to Chu et al. [14]. The MLR, MEM, and GWR statistical models are not only dependent on the distribution of ground stations but also have difficulty in applying many related increasing factors (e.g., meteorological conditions, land-use type, population, and road networks) to input parameter dimensions [14,15]. This implies that statistical models are likely to oversimplify the complicated relationships between PM2.5 and the input predictors. The CTM exhibits an inaccuracy issue due to natural sources and anthropogenic emission inventories, has substantial computational costs, and requires additional expertise to understand complex physical and chemical processes [16,17].
As an alternative way to solve these issues, nonlinear and nonparametric machine learning methods such as the artificial neural network, support vector regression, and random forest (RF) have been used to estimate ground-level concentrations of PM with satellite data, demonstrating more reliable accuracy than that of conventional numerical models and statistical approaches [18,19,20] due to their nonlinear computation [15,21]. Additionally, deep learning, which is considered the second generation of machine learning, has been suggested [22], and it has great potential to solve issues in geophysical research for analyzing complicated natural phenomena [15,21,22,23,24].
However, new approaches using deep learning have seldom been applied to estimate the spatial distribution of ground-level PM2.5. Only a few attempts have been made to estimate PM2.5 ground levels. Ong et al. [25] used a deep recurrent neural network to predict PM2.5, resulting in environmental monitoring with improved accuracy compared with that of numerical models; however, their method only performed well over ground monitoring sites. Li et al. [15] estimated ground-level PM2.5 by fusing satellite and station observations with deep learning, but they also used meteorological data from ground sites as the deep-learning input parameters when modeling daily PM2.5 using a polar orbit moderate resolution imaging spectroradiometer (MODIS/Terra) sensor. Sun et al. [26] adopted deeper and wider network model structures than those of Li et al. [15] to learn the complex spatiotemporal relationships of PM2.5 from large-scale observation data. The cross-validation values based on each ground site were statistically accurate in their research. However, they were limited in interpolated areas because they still used interpolated meteorological variables based on ground stations with inverse distance weighting methods as the input parameters for deep learning. Therefore, further applicability studies of deep learning are required to determine the optimal approach for more reliable and accurate PM2.5 ground-level spatial concentration data.
Consequently, the objective of our study was to spatially estimate ground-level PM2.5, primarily using high-spatiotemporal-resolution geostationary ocean color imager (GOCI) images and reanalysis data via the deep neural network (DNN) approach. Compared with previous studies that have used deep-learning methods [15,25,26], major differences and improvements were made in this study as follows.
Firstly, to estimate high-temporal-resolution (hourly) ground-level PM2.5 data, this study used GOCI satellite data, which can be used to monitor the diurnal variation in PM2.5 [27] and long-range transported air pollutants over Northeast Asia.
Secondly, this study directly used multispectral images of GOCI top of atmosphere (TOA) reflectance instead of GOCI-retrieved AOD products as the input parameters of the DNN model. Most previous studies have used satellite-based AOD to estimate ground-level PM2.5 [15], demonstrating reasonable results [14,19]. Although most research studies have sufficiently estimated the spatiotemporal distribution of AOD from the multispectral TOA reflectance of optical satellites, they still exhibit AOD product retrieval errors [28]. This means that the accumulative error of AOD retrieval from the satellite is propagated in the PM retrieval process, if AOD was used as an input parameter. In addition, because AOD estimation can be challenging due to the bright and nonlinear scattering characteristics of land surfaces [29,30], AOD-based estimation of PM2.5 has limitations over bright land-surface areas, similar to those of AOD retrieval [28].
Lastly, to enhance the application of DNN model performance from the spatial information perspective, near-surface atmospheric information from the unified model (UM) was used to improve the spatial accuracy of the PM concentration [31]. This means that the meteorological parameters of the ground stations were not used as input variables when simulating ground-level PM2.5, unlike in previous studies.

2. Study Area and Material

2.1. Area of Interest and Ground Measurements

This study focused on the Korean Peninsula, as illustrated in Figure 1, to estimate hourly ground-level P.M2.5, which was primarily due to the computational limitations of the DNN model caused by the high-spatiotemporal-resolution dimensions of the satellite and reanalysis data. The Korean Peninsula is located at mid-latitude and in the westerly wind zone, and it exhibits a monsoon climate that gives way to a cold continental climate in winter and a marine climate in summer [32]. This means that the retrieval accuracy of ground-level PM2.5 is lowered due to the high cloudiness of the rainy summer season.
The Korea Environment Corporation, a quasi-governmental organization under the Ministry of Environment, has installed over 300 ground observation stations across the Korean Peninsula to observe air quality. PM2.5 has been observed at 206 locations (Figure 1) since 2015 (accessed on 27 May 2021 from https://www.airkorea.go.kr). In this study, ground-truth data from 2015 and 2016 were used to optimize data-driven deep-learning models of PM2.5 and validate the accuracy of each model.
To evaluate the performance of the newly applied deep-learning network, PM2.5 data simulated with the Community Multiscale Air Quality (CMAQ) model version 5.1 [33] driven by meteorological inputs using the Weather Research and Forecasting (WRF) model version 3.8.1 [34] were also compared with ground measurements of PM2.5. Initial and boundary conditions for the WRF model were set by applying National Centers for Environmental Prediction (NCEP) Final (FNL) Operational Global Analysis data on 1° × 1° grids. The horizontal and vertical resolutions of the WRF and CMAQ models were 15 km × 15 km and 27 vertical sigma levels from the surface to 50 hPa, respectively. More details, such as about the chemical and physical configurations of the WRF and CMAQ models, are presented in a previous study [35].

2.2. Specifications of GOCI Satellite Data

In this study, we used TOA reflectance observed by GOCI onboard the Communication, Ocean, and Meteorological Satellite (COMS) to estimate hourly ground-level PM2.5. The reflectance data contain eight bands consisting of six visible and two near-infrared bands with a spatial resolution of 500 m. Although the sensor specifications of the GOCI satellites are predominately designed for ocean observation [36], GOCI is useful for estimating aerosol optical properties, especially those of land areas, because the nonlinear contribution of the bright surface reflectance decreases in the shortwave visible spectral region [29]. This means that an increase or decrease in the PM concentration can be observed by the GOCI satellite, primarily due to the lower error contribution of land-surface reflectance in shortwave blue channels. Detailed information on GOCI is provided in previous studies [27].
Additionally, a cloud mask of the GOCI image was applied to select clear sky areas for the retrieval of PM2.5 [27,37,38].

2.3. Meteorological Variables from UM Regional Data Assimilation and Prediction System (RDAPS) and Ancillary Data

In this study, we also used meteorological variables from the UM RDAPS [39] not only to improve the spatiotemporal performance of the DNN model but also to support the oversimplified relationship between the GOCI TOA reflectance and ground-level PM2.5. The following meteorological variables from the UM RDAPS model of the Korea Meteorological Administration (KMA) were used as additional input dimensions: wind direction and speed, surface pressure, planetary boundary layer height (PBLH), 2 m air temperature, dew point temperature, visibility, and relative humidity (accessed on 27 May 2021 from https://data.kma.go.kr/).
In addition to these variables, we used solar and satellite geometric conditions, including normalized difference vegetation index (NDVI), global 30 arc second digital elevation model (DEM), and land cover (LC) as input variables (accessed on 27 May 2021 from https://lpdaac.usgs.gov/tools/data-pool/). The NDVI and LC of MODIS were applied to consider the vitality of the vegetation and the state of the land surface.

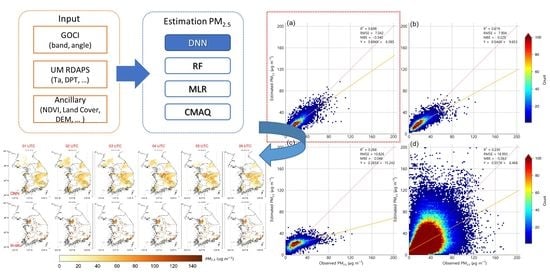
3. Methodology

3.1. Pre-Processing of Input Parameters for Training DNN

GOCI TOA, UM RDAPS reanalysis data, and other ancillary data (DEM, NDVI, and LC) have different spatial projections. Therefore, we converted all input data into orthographic map projections similar to those of the GOCI projection with a 4 km spatial resolution. Ancillary data were converted using the nearest-neighbor interpolation method. UM RDAPS estimates each meteorological variable based on a 12 km spatial resolution and 6 h intervals (00:00, 06:00, 12:00, and 18:00 coordinated universal time (UTC)). Differences in the spatiotemporal resolution between the reanalysis and GOCI satellite data were corrected by performing spatial interpolation with the Kriging method and temporal interpolation with a spline function. The Kriging method has been used in the assimilation process of weather data in many studies and has demonstrated reliable spatial interpolation performance [30,40,41]. For temporal interpolation with the spline function, most of the weather variables in previous studies showed curved cycles [42,43], and interpolation was performed with time-unit data through the spline function.
We validated the accuracy of the interpolated UM RDAPS variables (excluding PBLH) by calculating the correlation coefficient (R), root mean square error (RMSE), and mean bias error (MBE) with automatic synoptic observation station (ASOS) in situ meteorological variables provided by the KMA (Figure 2). In Figure 2, it can be seen that the interpolated UM RDAPS variables demonstrated statistically high matched patterns with the ASOS in situ measurements; however, the surface pressure showed a systematic deviation at each point. This is because the low spatial resolution of the UM RDAPS does not reflect the actual altitude characteristics of each in situ observation site. The wind speed exhibited a linear variation over time, but the wind direction uncertainty was high because observation data are provided in 20° direction intervals and are excluded from the input data. PBLH (Figure 2f) shows the monthly (January, March, May, July, September, and November) time average of the data before interpolation (diamond-shaped symbols) and after interpolation (solid lines) because actual measurement data could not be obtained. A similar temporal trend was observed to that of previous studies [42,44]. Finally, the interpolated spatiotemporal meteorological variables from UM RDAPS were used as additional input data for the DNN model.

3.2. DNN Approach

In this study, we adopted the Python deep-learning library of Keras to estimate ground-level PM2.5. A DNN is a supervised training method with a feed-forward network structure that utilizes error backpropagation to determine the weight and bias of each hidden node. Thus, it requires true values, such as in situ measurements [17]. The DNN is composed of one input layer, multiple hidden layers, and one output layer. The number of hidden layers is typically greater than three, and the DNN consists of n time-hidden input nodes [17,45]. The structure of the DNN influences the performance of the estimation model; thus, we examined several training model structures with various parameter combinations, as presented in Table 1. In this study, Keras Tuner was used to determine the optimal hyperparameters for the deep-learning model, which was determined to be four hidden layers, including 512, 512, 1024, and 1024 hidden nodes for each layer, with L1 regularization of 0.001, batch normalization, and the rectified linear unit (ReLu) activation function. In addition, Adam optimization with a learning rate of 0.05 and a dropout rate of 0.3 were determined as the optimal hyperparameters.
For reference, the random forest (RF) approach was also applied to compare the performance of the newly applied DNN ground-level PM2.5 estimation, because it demonstrates high predictive performance by calculating the results of several decision trees using the ensemble technique [19,20,46,47]. In this study, 72 model structures were tested based on independent variables such as the number of decision trees, maximum tree depth, and the percentage of data per column used for training to predict the concentration of PM2.5. The results of the analysis illustrated that the final RF used 70% of the data per column for 40 decision trees, 12 input nodes per decision tree, and 80% of the total data for each decision tree.
In this study, two validation approaches were applied to evaluate the temporal and spatial performances of the deep-learning model: hold-out validation and k-fold cross-validation. For the hold-out validation, we separated the total matchup datasets into three parts in chronological order: training data (60%), validation data (20%), and test data (20%). Fivefold cross-validation was performed by dividing the PM ground observation stations into five groups, as illustrated in Figure 1. Each cross-validation dataset was randomly composed of 114 points (approximately 55% of training data) at 206 observation points; 54 points (approximately 26% of validation) of data were utilized during the training process, and the remaining 38 points (approximately 18% of test data) were used as the final model accuracy test data. For both the hold-out validation and the cross-validation approaches, the training data were used to optimize the deep-learning model, and the validation data were used to reduce overfitting problems based on the early stop approach applied in the training process. The remaining test data were used to evaluate how well the deep-learning model reflected the spatiotemporal characteristics of PM2.5. As a reference, all matchup datasets were normalized from their physical values to 0–1 float values using minimum and maximum values over 2 years.

4. Results

Figure 3 displays scatterplots depicting the correlation between the ground-truth PM2.5 measurements and estimated PM2.5 values calculated by each model based on the hold-out validation. Overall, the DNN demonstrates the highest accuracy (RMSE = 7.042 μg/m3, MBE = −0.34 μg/m3, and coefficient of determination (R2) = 0.698) when comparing the ground measurements of PM2.5. RF is less accurate than the DNN, with RMSE = 7.904 μg/m3, MBE = 0.225 μg/m3, and R2 = 0.619. Both RF and the DNN tend to underestimate above a certain threshold (over 25 μg/m3), but RF has a greater underestimation, which means that its uncertainty is greater for high concentrations. Regarding MLR, it is well clustered, but the calculation range is concentrated in a narrower range compared to that of the actual values, and the maximum output value is not reflected in high concentration cases within 40 μg/m3. The predicted values from the CMAQ simulations were distributed over a wide range regardless of the actual measurement, and the RMSE and MBE were higher than those of the other methods. However, unlike the satellite-based method, prediction is possible for 24 h a day, and the CMAQ model contains more data for the same period since there are no missing areas due to cloud cover. In Figure 3d, the time range (08~23 UTC) that is not observed by GOCI is excluded.
To evaluate the spatial generalization, fivefold cross-validation was performed for the DNN, RF, and MLR by dividing the dataset into five station groups, as illustrated in Figure 1. In the case of CMAQ based on the physical model, we did not perform cross-validation since the performance of generalization for CMAQ is better than the data-driven models of the DNN, RF, and MLR, which were trained using the ground measurements [21,35]. The results are presented in Table 2, and the total cross-validation results of the RMSE, MBE, and R2 for the DNN are 9.17 μg/m3, 0.293 μg/m3, and 0.49 μg/m3, respectively, and the results of the fivefold cross-validations are less accurate than those of the hold-out validation of the deep-learning model. This means that the spatial variation exhibits a complicated spatial pattern and requires additional parameters to reflect the characteristics of spatial PM2.5. Although the R2 is low because of the underestimated pattern of high PM2.5, the RMSE and MBE displayed reliable and accurate values of less than 10 μg/m3 and 1 μg/m3, respectively, when compared with previous results [15,19,20,25,26,48]. When considering the RF model as a comparative analysis, the statistical values may vary according to the data type, pre-processing approach, adopted model, and validation method. The proposed DNN model appears to produce reliable estimates of spatiotemporal PM2.5 when compared to those of the RF model.

5. Discussion

Finally, we confirmed the spatial calculation ability of the DNN model for the case of high concentrations in 2017. Figure 4 displays the results of the hourly spatial maps of ground-level PM2.5 on 19 January 2017 (from 01:00 (10:00) to 06:00 (15:00) UTC (KST)) for cases of high PM2.5 concentrations. Except for areas that are not observable due to clouds, high concentration areas estimated using the DNN model were well matched with the ground-truth PM2.5. Similar to the accuracy analysis results, the spatial variation in the DNN is consistent; however, it tends to underestimate concentrations, especially for high PM2.5 areas. Nevertheless, it was determined that the utility of the DNN approach using satellite and reanalysis data is high because it can observe diurnal and spatial changes of PM2.5 with reliable accuracy.
As this study is based on the GOCI sensor, there are several limitations. First, the GOCI is a sensor whose main purpose is ocean color observation, and it is impossible to observe at night due to only being equipped with a visible channel. Second, there is an error possibility for high concentration cases via residual cloud effects due to the absence of an IR channel. The above problems can be solved by fusion with meteorological data from satellites that observe a wide range of wavelengths, such as the Geo-KOMPSAT-2A/Advanced Meteorological Imager (GK-2A/AMI).

6. Conclusions

In this study, we estimated ground-level PM2.5 via a deep-learning approach using TOA reflectance observed with GOCI satellite and meteorological variables of reanalysis data, demonstrating that the proposed DNN model can effectively reflect the spatial characteristics of PM2.5 over the Korean Peninsula compared with conventional RF, MLR, and CMAQ methods. Overall, data-driven models, such as the DNN and RF models, showed more reliable PM2.5 retrieval than that of conventional MLR and CMAQ. In addition, the DNN method exhibited higher accuracy than the RF method for both the validation approaches due to its deeper and more complicated network structure. Conventional MLR tended to converge to a certain value, with a low error rate but also a lower matching rate.
Although the DNN demonstrated that the temporal variations of PM2.5 were sufficiently calculated according to the results of the hold-out validation, the spatial characteristics estimates remain a limit, despite applying the GOCI satellite and reanalysis data, due to the complexity of ground-level PM2.5, according to the cross-validation results. This implies that additional spatial variables (population, road networks, etc.) should be considered to reflect the substantially large spatial variability of PM2.5. Furthermore, compared to CMAQ, the DNN is limited in estimating PM for cloud areas and daily changes, including nighttime. Nevertheless, the suggested method enables the observation of the spatial variation in actual ground PM2.5, unlike previous studies, because the data from meteorological stations were not used as input data for the DNN model. Compared with other AOD-based PM2.5 estimations, the model has several advantages: (1) the AOD calculation process is independent of errors and (2) time and computing resources are saved in this process.

Author Contributions

Conceptualization, C.L. and J.Y. (Jongmin Yeom); methodology, C.L., S.J., K.L., and J.Y. (Jongmin Yeom); validation, C.L. and J.Y. (Jongmin Yeom); writing—original draft preparation, J.Y. (Jongmin Yeom); writing—review and editing, C.L., K.L., S.K., J.Y. (Jinhyeok Yu), S.J., and J.Y. (Jongmin Yeom); supervision, S.J. and J.Y. (Jongmin Yeom); funding acquisition, C.L. and J.Y. (Jongmin Yeom) All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Institute of Environmental Research, funded by the Ministry of Environment of the Republic of Korea (grant number NIER-2019-01-01-027) and the Korea Aerospace Research Institute (grant number FR21J00).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

We thank the Korea Institute of Ocean Science and Technology (KIOST) for providing the GOCI data.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Xu, J.-W.; Martin, R.V.; van Donkelaar, A.; Kim, J.; Choi, M.; Zhang, Q.; Geng, G.; Liu, Y.; Ma, Z.; Huang, L.; et al. Estimating ground-level PM2.5 in eastern China using aerosol optical depth determined from the GOCI satellite instrument. Atmos. Chem. Phys. 2015, 15, 13133–13144. [Google Scholar] [CrossRef] [Green Version]
  2. Guo, Y.; Tang, Q.; Gong, D.-Y.; Zhang, Z. Estimating ground-level PM2.5 concentrations in Beijing using a satellite-based geographically and temporally weighted regression model. Remote Sens. Environ. 2017, 198, 140–149. [Google Scholar] [CrossRef]
  3. Butt, E.W.; Turnock, S.T.; Rigby, R.; Reddington, C.L.; Yoshioka, M.; Johnson, J.S.; Regayre, L.A.; Pringle, K.J.; Mann, G.W.; Spracklen, D.V. Global and regional trends in particulate air pollution and attributable health over the past 50 years. Environ. Res. Lett. 2017, 12, 104017. [Google Scholar] [CrossRef]
  4. IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
  5. Scott, C.E.; Rap, A.; Spracklen, D.V.; Forster, P.M.; Carslaw, K.S.; Mann, G.W.; Pringle, K.J.; Kivekäs, N.; Kulmala, M.; Lihavainen, H.; et al. The direct and indirect radiative effects of biogenic secondary organic aerosol. Atmos. Chem. Phys. 2014, 14, 447–470. [Google Scholar] [CrossRef] [Green Version]
  6. Armstrong, B.G. Effect of measurement error on epidemiological studies of environmental and occupational exposures. Occup. Environ. Med. 1998, 55, 651–656. [Google Scholar] [CrossRef] [Green Version]
  7. Liu, Y.; Koutrakis, P.; Kahn, R. Estimating fine particulate matter component concentrations and size distributions using satellite-retrieved fractional aerosol optical depth: Part 2-A case study. J. Air Waste Manag. Assoc. 2007, 57, 1360–1369. [Google Scholar] [CrossRef]
  8. Engel-Cox, J.A.; Hoff, R.M.; Haymet, A.D.J. Recommendations on the use of satellite remote-sensing data for urban air quality. J. Air Waste Manag. Assoc. 2004, 54, 1360–1371. [Google Scholar] [CrossRef]
  9. Xiao, Q.; Wang, Y.; Chang, H.H.; Meng, X.; Geng, G.; Lyapustin, A.; Liu, Y. Full-coverage high-resolution daily PM2.5 estimation using MAIAC AOD in the Yangtze River Delta of China. Remote Sens. Environ. 2017, 199, 437–446. [Google Scholar] [CrossRef]
  10. Geng, G.; Zhang, Q.; Martin, R.V.; van Donkelaar, A.; Huo, H.; Che, H.; Lin, J.; He, K. Estimating long-term PM2.5 concentrations in China using satellite-based aerosol optical depth and a chemical transport model. Remote Sens. Environ. 2015, 166, 262–270. [Google Scholar] [CrossRef]
  11. Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface satellite, and meteorological products: Multiple regression approach. J. Geophys. Res. 2009, 114, D14205. [Google Scholar] [CrossRef] [Green Version]
  12. Ma, Z.; Liu, Y.; Zhao, Q.; Liu, M.; Zhou, Y.; Bi, J. Satellite-derived high resolution PM2.5 concentrations in Yangtze River Delta Region of China using improved linear mixed effects model. Atmos. Environ. 2016, 133, 156–164. [Google Scholar] [CrossRef]
  13. Luo, J.; Du, P.; Samat, A.; Xia, J.; Che, M.; Xue, Z. Spatiotemporal pattern of PM2.5 concentrations in Mainland China and analysis of its influencing factors using geographically weighted regression. Sci. Rep. 2017, 7, 40607. [Google Scholar] [CrossRef] [PubMed]
  14. Chu, Y.; Liu, Y.; Li, X.; Liu, Z.; Lu, H.; Lu, Y.; Mao, Z.; Chen, X.; Li, N.; Ren, M.; et al. A review on predicting ground PM2.5 concentration using satellite aerosol optical depth. Atmosphere 2016, 7, 129. [Google Scholar] [CrossRef] [Green Version]
  15. Li, T.; Shen, H.; Yuan, Q.; Zhang, X.; Zhang, L. Estimating ground-level PM2.5 by fusing satellite and station observations: A geo-intelligent deep learning approach. Geophys. Res. Lett. 2017, 44, 11985–11993. [Google Scholar] [CrossRef] [Green Version]
  16. Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Kahn, R.; Levy, R.; Verduzco, C.; Villeneuve, P.J. Global estimates of ambient fine particulate matter concentrations from satellite-based aerosol optical depth: Development and application. Environ. Health Perspect. 2010, 118, 847–855. [Google Scholar] [CrossRef] [Green Version]
  17. Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
  18. Chen, G.; Li, S.; Knibbs, L.D.; Hamm, N.A.; Cao, W.; Li, T.; Guo, J.; Ren, H.; Abramson, M.J.; Guo, Y. A machine learning method to estimate PM2.5 concentrations across China with remote sensing, meteorological and land use information. Sci. Total Environ. 2018, 636, 52–60. [Google Scholar] [CrossRef]
  19. Park, S.; Shin, M.; Im, J.; Song, C.K.; Choi, M.; Kim, J.; Lee, S.; Park, R.; Kim, J.; Lee, D.W.; et al. Estimation of ground-level particulate matter concentrations through the synergistic use of satellite observations and process-based models over South Korea. Atmos. Chem. Phys. 2019, 19, 1097–1113. [Google Scholar] [CrossRef] [Green Version]
  20. Park, S.; Lee, J.; Im, J.; Song, C.K.; Choi, M.; Kim, J.; Lee, S.; Park, R.; Kim, S.M.; Yoon, J.; et al. Estimation of spatially continuous daytime particulate matter concentrations under all sky conditions through the synergistic use of satellite-based AOD and numerical models. Sci. Total Environ. 2020, 713, 136516. [Google Scholar] [CrossRef] [PubMed]
  21. Yeom, J.M.; Park, S.; Chae, T.; Kim, J.Y.; Lee, C.S. Spatial assessment of solar radiation by machine learning and deep neural network models using data provided by the COMS MI geostationary satellite: A case study in South Korea. Sensors 2019, 19, 2082. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [Green Version]
  23. Scher, S. Toward data-driven weather and climate forecasting: Approximating a simple general circulation model with deep learning. Geophys. Res. Lett. 2019, 45, 12616–12622. [Google Scholar] [CrossRef] [Green Version]
  24. Yeom, J.M.; Deo, R.C.; Adamowski, J.F.; Park, S.; Lee, C.S. Spatial mapping of short-term solar radiation prediction incorporating geostationary satellite images coupled with deep convolutional LSTM networks for South Korea. Environ. Res. Lett. 2020, 15, 094025. [Google Scholar] [CrossRef]
  25. Ong, B.T.; Sugiura, K.; Zettsu, K. Dynamically pre-trained deep recurrent neural networks using environmental monitoring data for predicting PM2.5. Neural Comput. Appl. 2016, 27, 1553–1566. [Google Scholar] [CrossRef] [Green Version]
  26. Sun, Y.; Zeng, Q.; Geng, B.; Lin, X.; Sude, B.; Chen, L. Deep learning architecture for estimating hourly ground-level PM2.5 using satellite remote sensing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1343–1347. [Google Scholar] [CrossRef]
  27. Choi, M.; Kim, J.; Lee, J.; Kim, M.; Park, Y.J.; Holben, B.; Eck, T.F.; Li, Z.; Song, C.H. GOCI Yonsei aerosol retrieval version 2 products: An improved algorithm and error analysis with uncertainty estimation from 5-year validation over East Asia. Atmos. Meas. Tech. 2018, 11, 385–408. [Google Scholar] [CrossRef] [Green Version]
  28. Shen, H.; Li, T.; Yuan, Q.; Zhang, L. Estimating regional ground-level PM2.5 directly from satellite top-of-atmosphere reflectance using deep belief networks. J. Geophys. Res. Atmos. 2018, 123, 13875–13886. [Google Scholar] [CrossRef] [Green Version]
  29. Von Hoyningen-Huene, W.; Joon, Y.; Vountas, M.; Istomina, G.; Rohen, G.; Dinter, T.; Kokhanovsky, A.A.; Burrows, J.P. Retrieval of spectral aerosol optical thickness over land using ocean color sensors MERIS and SeaWiFS. Atmos. Meas. Tech. 2011, 4, 151–171. [Google Scholar] [CrossRef] [Green Version]
  30. Li, X.; Cheng, G.; Lu, L. Spatial analysis of air temperature in the Qinghai-Tibet Plateau. Antarct. Alp. Res. 2005, 37, 246–252. [Google Scholar] [CrossRef]
  31. Li, T.; Shen, H.; Zeng, C.; Yuan, Q.; Zhang, L. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China: Methods and assessment. Atmos. Environ. 2017, 152, 477–489. [Google Scholar] [CrossRef] [Green Version]
  32. Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
  33. Byun, D.W.; Ching, J.K.S. Science Algorithms of the EPA Models-3 Community Multiscale Air Quality (CMAQ) Modeling System; EPA/600/R99/030 (NTIS PB2000-100561); U.S. Environmental Protection Agency: Washington, DC, USA, 1999. [Google Scholar]
  34. Skamarock, C.; Klemp, B.; Dudhia, J.; Gill, O.; Barker, D.; Duda, G.; Huang, X.; Wang, W.; Powers, G.A. Description of the Advanced Research WRF Version 3. Available online: https://doi.org/10.5065/D68S4MVH (accessed on 27 May 2008).
  35. Byun, D.; Schere, K.L. Review of the governing equations, computational algorithms, and other components of the Models-3 community multiscale air quality (CMAQ) modeling system. Appl. Mech. Rev. 2006, 59, 51–77. [Google Scholar] [CrossRef]
  36. Yeom, J.M.; Kim, H.O. Comparison of NDVIs from GOCI and MODIS data towards improved assessment of crop temporal dynamics in the case of paddy rice. Remote Sens. 2015, 7, 11326–11343. [Google Scholar] [CrossRef] [Green Version]
  37. Hsu, N.C.; Jeong, M.J.; Bettenhausen, C.; Sayer, A.M.; Hansell, R.; Seftor, C.S.; Huang, J.; Tsay, S.C. Enhanced Deep Blue aerosol retrieval algorithm: The second generation. J. Geophys. Res. Atmos. 2013, 118, 9296–9315. [Google Scholar] [CrossRef]
  38. Pinty, B.; Verstraete, M.M. GEMI: A non-linear index to monitor global vegetation from satellites. Vegetation 1992, 101, 15–20. [Google Scholar] [CrossRef]
  39. Park, S.; Lee, D.U.; Seo, J.W. Operational wind wave prediction system at KMA. Mar. Geod. 2009, 32, 133–150. [Google Scholar] [CrossRef]
  40. Mahdian, M.H.; Bandarabady, S.R.; Sokouti, R.; Banis, Y.N. Appraisal of the geostatistical methods to estimate monthly and annual temperature. J. Appl. Sci. 2009, 9, 128–134. [Google Scholar] [CrossRef]
  41. Nguyen, X.T.; Nguyen, B.T.; Do, K.P.; Bui, Q.H.; Nguyen, T.N.T.; Vuong, V.Q.; Le, T.H. Spatial interpolation of meteorological variables in Vietnam using the Kriging method. J. Inf. Process. Syst. 2015, 11, 134–147. [Google Scholar] [CrossRef] [Green Version]
  42. Chu, Y.; Li, J.; Li, C.; Tan, W.; Su, T.; Li, J. Seasonal and diurnal variability of planetary boundary layer height in Beijing: Intercomparison between MPL and WRF results. Atmos. Res. 2019, 227, 1–13. [Google Scholar] [CrossRef]
  43. Xie, M.; Zhu, K.; Wang, T.; Feng, W.; Gao, D.; Li, M.; Li, S.; Zhuang, B.; Han, Y.; Chen, P.; et al. Changes in regional meteorology induced by anthropogenic heat and their impacts on air quality in South China. Atmos. Chem. Phys. 2016, 16, 15011–15031. [Google Scholar] [CrossRef] [Green Version]
  44. Chang, Y.; Zou, Z.; Deng, C.; Huang, K.; Collett, J.L.; Lin, J.; Zhuang, G. The importance of vehicle emissions as a source of atmospheric ammonia in the megacity of Shanghai. Atmos. Chem. Phys. 2016, 16, 3577–3594. [Google Scholar] [CrossRef] [Green Version]
  45. Zhang, D.; Zhang, W.; Huang, W.; Hong, Z.; Meng, L. Upscaling of surface soil moisture using a deep learning model with VIIRS RDR. ISPRS Int. J. Geo. Inf. 2017, 6, 130. [Google Scholar] [CrossRef]
  46. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  47. Geng, G.; Meng, X.; He, K.; Liu, Y. Random forest models for PM2.5 speciation concentrations using MISR fractional AODs. Environ. Res. Lett. 2020, 15, 034056. [Google Scholar] [CrossRef]
  48. Zang, L.; Mao, F.; Guo, J.; Gong, W.; Wang, W.; Pan, Z. Estimating hourly PM1 concentrations from Himawari-8 aerosol optical depth in China. Environ. Pollut. 2018, 241, 654–663. [Google Scholar] [CrossRef] [PubMed]
Remotesensing 13 02121 g001 550
Figure 1. Map of study area denoting elevations and locations of in situ measurements, which were categorized into five groups for cross-validation.
Figure 1. Map of study area denoting elevations and locations of in situ measurements, which were categorized into five groups for cross-validation.
Remotesensing 13 02121 g001
Remotesensing 13 02121 g002 550
Figure 2. Comparison of in situ meteorological variables and interpolated UM RDAPS: (a) dew point temperature; (b) surface pressure; (c) wind speed; (d) 2 m height air temperature; (e) relative humidity; and (f) PBLH.
Figure 2. Comparison of in situ meteorological variables and interpolated UM RDAPS: (a) dew point temperature; (b) surface pressure; (c) wind speed; (d) 2 m height air temperature; (e) relative humidity; and (f) PBLH.
Remotesensing 13 02121 g002
Remotesensing 13 02121 g003 550
Figure 3. Scatterplots describing correlations between ground-truth PM2.5 measurements and estimated PM2.5 values calculated by each model: (a) DNN; (b) RF; (c) MLR; and (d) CMAQ.
Figure 3. Scatterplots describing correlations between ground-truth PM2.5 measurements and estimated PM2.5 values calculated by each model: (a) DNN; (b) RF; (c) MLR; and (d) CMAQ.
Remotesensing 13 02121 g003
Remotesensing 13 02121 g004 550
Figure 4. Spatial distributions of ground-level PM2.5 concentrations on 19th January 2017 (from 01:00 to 06:00 UTC). The top row figures are hourly spatial maps of PM2.5 from the DNN, and the bottom row figures are the corresponding spatiotemporal measurements of PM2.5 from selected ground stations.
Figure 4. Spatial distributions of ground-level PM2.5 concentrations on 19th January 2017 (from 01:00 to 06:00 UTC). The top row figures are hourly spatial maps of PM2.5 from the DNN, and the bottom row figures are the corresponding spatiotemporal measurements of PM2.5 from selected ground stations.
Remotesensing 13 02121 g004
Table
Table 1. Hyperparameter range used to select the optimal deep-learning model structure for estimating ground-level PM2.5.
Table 1. Hyperparameter range used to select the optimal deep-learning model structure for estimating ground-level PM2.5.
ParameterConfiguration
Number of hidden nodes641282565121024
Number of hidden layers3–44–64–66–86–8
L1 regularizationFalse, 0.01, 0.001, and 0.0001
L2 regularizationFalse, 0.01, 0.001, and 0.0001
Activation functionReLu, Leaky ReLu, and exponential linear unit (ELU)
OptimizationAdam and root mean square propagation (RMSProp)
Learning rate0.05, 0.001, and 0.005
Dropout rate0.1, 0.2, and 0.3
Table
Table 2. Summary of the DNN, RF, and MLR cross-validation results.
Table 2. Summary of the DNN, RF, and MLR cross-validation results.
MethodRMSEMBER2
DNN9.1660.2930.49
RF9.3420.3370.474
MLR11.133−0.04280.251
RMSE and MBE are in μg/m−3.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Lee, C.; Lee, K.; Kim, S.; Yu, J.; Jeong, S.; Yeom, J. Hourly Ground-Level PM2.5 Estimation Using Geostationary Satellite and Reanalysis Data via Deep Learning. Remote Sens. 2021, 13, 2121. https://doi.org/10.3390/rs13112121

AMA Style

Lee C, Lee K, Kim S, Yu J, Jeong S, Yeom J. Hourly Ground-Level PM2.5 Estimation Using Geostationary Satellite and Reanalysis Data via Deep Learning. Remote Sensing. 2021; 13(11):2121. https://doi.org/10.3390/rs13112121

Chicago/Turabian Style

Lee, Changsuk, Kyunghwa Lee, Sangmin Kim, Jinhyeok Yu, Seungtaek Jeong, and Jongmin Yeom. 2021. "Hourly Ground-Level PM2.5 Estimation Using Geostationary Satellite and Reanalysis Data via Deep Learning" Remote Sensing 13, no. 11: 2121. https://doi.org/10.3390/rs13112121

APA Style

Lee, C., Lee, K., Kim, S., Yu, J., Jeong, S., & Yeom, J. (2021). Hourly Ground-Level PM2.5 Estimation Using Geostationary Satellite and Reanalysis Data via Deep Learning. Remote Sensing, 13(11), 2121. https://doi.org/10.3390/rs13112121

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop