1. Introduction
The radar altimetry measuring the flight altitude is widely used in airborne and spaceborne remote sensing [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11]. The principles of radar altimetry are very close to radio range finding, but it has a number of specific features associated primarily with the location objects, which are, in general, extended, rough and diverse surfaces. For precision radar altimeters (PRAs), the features of the reflected wideband LFM (Linear Frequency Modulation) signals from the sea surface illuminated from high altitudes such as satellites, are presented in detail in [
5,
12,
13] and others. Height of the altimeter
H0 is generally understood as the distance from PRA to the average calm sea surface level. A phenomenological approach method is used to analyze the characteristics of echo signals reflected from the sea surface. The backscattering pattern is assumed Gaussian in this model. All the sea surface statistics are presented in the illuminated surface [
1,
2,
12,
14].
As we showed in our previous research [
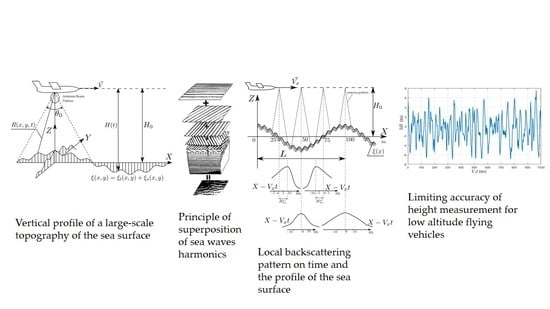
15], for altitudes of the flying vehicles less than, for example, 500 m, the analysis of the characteristics of radio signals reflected from statistically uneven sea surfaces based on the stationary representation of phenomenological model becomes incorrect. It is because the size of the area illuminated on the sea surface is considerable with the correlation radius of the sea surface roughness. Consequently, the reflected signals are formed by the reflections from single large-scale roughness and many smaller roughness of the surface on its large ones. This is a typical case of an unsteady state. Under this condition, the formation of the height estimation in PRA can be carried out with respect to a large-scale relief. Moreover, the local backscattering pattern, in contrast to other known concepts of the backscattering pattern, depends on time and it is also a function, not only of the surface, but of the relative position of the flying vehicle to the sea surface. Its width is determined by the statistical characteristics of small roughness of the surface on the large waves. In this case, the estimate of the height of the PRA depends on random functions that describe large sea surface roughness and their slopes. The operation feature of a PRA flying at low altitudes estimates the vertical profile of large-scale topography as shown in
Figure 1, which is illustrated in our previous article [
15].
2. Effect of Local Backscattering Pattern of the Sea Surface on Reflected Signal of PRA at Low Altitudes
The surface is defined as a superposition of large
and small
roughness that model large wind waves (or swell waves) and small wind waves (or ripples) on the large wave surface:
To find the expression for the voltage at the input of the discriminator, we assume that the number of small irregularities within the irradiated surface is large, and the two-dimensional law of distribution of small irregularities is normal with variance .
Then the final expressions for the voltage values at the input of the discriminator [
15]:
where
A is the scale factor,
G(
s,
t) is the PRA antenna pattern,
R0 is the distance to the average level of the surface,
,
is the autocorrelation function of the probing signal,
ds is the elementary site on the surface,
t is the time,
c is the speed of light,
Glbp is the local backscattering pattern, which is defined by expression
ls is the spatial correlation interval of the small irregularities,
is an effective width of the main lobe of the local backscattering pattern, which is determined by the statistical characteristics of small irregularities.
Figure 2 shows the dependence of the local backscattering pattern on time and the surface profile for different widths of the backscattering pattern. The local backscattering pattern is not only a function of sea surface reflective properties but also a function of time. It depends on the relative position of the flying vehicle from the sea surface, as well as on the presence of small ripples on the sea surface [
15].
3. Formulation of the Height Estimate in a Precision Radar Altimeter
Using (2), we find an expression of the discriminator tracking system for height estimation:
where
is ambiguity function of square of the envelope of the autocorrelation function of the LFM signal and the reference pulse at
frequency shift;
is the current detuning of the height estimation
in the discriminator,
is the distance between the reference signals.
Thus, the discriminator characteristic of PRA, which depends on time and slope of the surface, changes randomly during the flight. At the tracking point we can equalize (4) to zero and obtain the integral equation
With the integral method of signal processing (“centroid”), when reference pulses are much wider than the reflected signals and the mutual uncertainty function slowly changes from
, the following approximation is used
Taking into account (6), we transform the integral Equation (5) to the following form:
where
is a height estimation.
Solving (7) with respect to
, we obtain
Expression (8) defines the algorithm of formulating a height estimation expression with signal integration processing. Due to that the integrands depend on random functions describing large roughness and their slopes, direct calculation of (8) in the general case is impossible.
To analyze the expression of PRA, we consider a special case. Let the derivative of large roughness be constant within the illumination spot. We use antenna pattern approximation to calculate (8):
Substituting (9) into (8) and considering that
the following expression is obtained:
In (10)
is the bias of the estimate of the height, time-varying, depending on the slopes of major roughness
where
is the effective beam width taking into account antenna pattern and local backscattering pattern, and
is the component of the height estimation related to surface topography
where
.
From (10) height estimation at the output of the tracking system of the PRA is the sum of three factors: the first is the height to the average level; the second is the bias of the estimate of the height, time-varying, depending on the slopes of major roughness; the third is the component related to surface topography.
4. Description of the Sea Surface Roughness
The problem of describing the sea surface roughness can be solved using the principle of superposition (
Figure 3), the overlay of simple harmonic waves. Such a superposition underlies the spectral method for sea wave research.
The task of describing an irregular sea surface is solved using the superposition principle represented as the sum of large number of elementary waves [
16,
17]:
where the sea surface, in this case, is subject to the laws of statistics. It is assumed that the rough sea surface with fully developed waves is locally uniform, stationary, subject to the normal distribution law and has the property of ergodicity. The function
S(ω,θ) is a spectral function of two-dimensional energy spectrum.
Among many approximation expressions for the spectra of sea waves, there is a widely used group of so-called exponential spectra. Often used “Joint North Sea Wave Project” (JONSWAP) where the spectrum has the following form [
18,
19]:
where
The parameter
γ is usually 3.3, but for more accurate mathematical calculations the value can be calculated depending on the significant wave height
Hm and the repetition period of sea waves
Tp:
and lies in the range from 1 to 7.
Frequency spectrum specifies the fluctuations of the sea surface at a fixed point and, therefore, cannot give any information about the distribution of elementary waves energy depending on their direction of propagation. Therefore, frequency-angular spectrum of waves , where function S(ω) describes the distribution of wave energy in frequencies, and the function Q(ω,θ) is responsible for angular distribution, is commonly used.
The cos
2l θ function is usually taken as a mathematical model of angular spectrum
. It is easy to use, although it has not been confirmed experimentally. Sometimes its extended version is used [
20]:
where
,
The exponent
l depends on the wind strength and frequency but known approximations of these dependences differ significantly. For spectrum of wind waves
l = 1~4, and for swell
l = 6.
The JONSWAP spectrum has proven itself well for describing developed wind waves, however, it describes only large-scale waves, therefore, the high-frequency part is worked out much worse than the low-frequency one (
Figure 4). The real process of wave formation includes, in addition to wind waves, waves of various nature, among which there are swell waves as well. In other words, the formation of waves on the sea surface depends on a very large number of factors, some of which we may not even know yet.
In modern science, the calculation of the sea surface is performed using a two-humped spectrum of sea waves. The imposition of swell waves on the wind component generates two “humps” in the form of sea wave spectrum, as shown in
Figure 5.
The general structure of the spectrum has the form
where
is a function that describes the shape of a “hump” in the form of a JONSWAP spectrum.
In accordance with the spectral model selected, the approximation of the sea surface will be written as:
where
θp is the angle of the wind propagation direction.
5. Calculation of Limiting Accuracy of Height Measurement in Sea Wave Spectrum Domain
For the calculation of the estimation error, i.e., limiting accuracy of PRA height measurement of a flying vehicle at low over the sea surface, we need reasonable approximations for the large-scale roughness of the sea surface with a deterministic function . In this research, we used the spectral representation of the sea surface instead of a harmonic function approach.
To numerically implement the estimation of the PRA altitude, the operations of differentiation and integration of the expression for the approximation of the sea surface should be performed at
x =
y = 0. Then the
x derivative of the selected sea surface approximation
ξx(
t) has the following form:
The integral included in the (12) is also required to calculate.
As a result, we have the following expression for the height estimation
True altitude of the flying vehicle is determined from the expression
Comparing
H(
t) and
H*(
t), we could derive results for the limiting accuracy of the PRA operating at low altitudes above the sea surface, as shown in
Figure 6 and
Figure 7, where
Uw is wind speed, Δ
H(
t) =
H*(
t) −
H0 and
, limiting accuracy.
6. Conclusions
When the PRA flying at low altitudes during its surface profile measurement, the reflective property of the sea surface is expressed as a function of
, which also depends on time and relative position of the flying vehicle to the sea surface in contract to the well-known concepts of backscattering pattern; and its effective beam width is determined by the statistical characteristics of small-scale roughness on the surface of large wind waves; and the location of the maximum of the local backscattering pattern is determined by the derivative of the large-scale roughness of the sea surface, and when the backscattering pattern is wide, the symmetry of the local backscattering pattern on the slopes of the topography is not maintained; all of which are obtained and concluded in our previous research [
15].
The direct calculation of the height estimate of the PRA altitude during its signal processing stage is difficult since the integrands in (8) are determined by the random functions which describe large-scale roughness of the sea surface and their slopes.
The height estimation at the output of the tracking system of the PRA is the sum of three factors: the first is the height to the average sea level; the second is the bias from the height, which is time-varying and depends on the slopes of large-scale roughness; the third is the component related to the sea surface topography.
For a quantitative calculation of the estimation error of the height measurement of a flying PRA at low altitudes, a reasonable approximation for the large-scale roughness of the sea surface by the deterministic function is required.
Two-humped frequency spectrum and angular spectrum of the form cos2l θ are used for the approximation of the large-scale roughness.
Analysis of the results shows that as the width of the antenna beam pattern increases by means of flight altitude increasing, the width of the local backscattering pattern and the sea illumination area are increased, which lead to the increase of the estimation error. In this scenario, the systematic error tends to grow unlimitedly, and the random component tends to be constant equal to the standard deviation of the wave height, i.e., the PRA smooths the sea surface roughness.
The approximation developed in this study does not consider small-scale roughness associated with the surface viscosity of the liquid on the sea surface of large wind waves. Therefore, the values of the narrow local backscattering pattern from small-scale roughness in this case were set artificially. Since the inclusion of ripples on waves was not fully covered in this study, it will make sense to consider this issue separately in future works.
The results obtained from this study for the analysis of limiting accuracy of a PRA in a flying vehicle at low altitude above the sea surface, allows to obtain reasonable system parameter values, which minimize the measurement errors of the flight altitude.