In this section, ensemble learning and extreme learning machine are briefly introduced, and the proposed ensemble-learning-based autofocus method is described in detail.
3.1. Ensemble Scheme
Ensemble learning combines some weak but diverse models with certain combination rules to form a strong model. Key to ensemble learning are individual learners with diversity and the combination strategy. In ensemble learning, individual learners can be homogeneous or heterogeneous. A homogeneous ensemble consists of members with a single-type base learning algorithm, such as the decision tree, support vector machine or neural network, while a heterogeneous ensemble consists of members with different base learning algorithms. Homogeneous learners are most commonly used [
42].
Classical ensemble methods include bagging, boosting, and stacking-based methods. These methods have been well-studied in recent years and applied widely in different applications [
43]. The key idea of a boosting-based algorithm is: the samples used to train the current individual learner are weighted according to the learning errors of the previous individual learner. Thus, the larger the errors in a sample used by the previous individual learner, the greater the weight that is set for this sample, and vice versa [
44]. Therefore, in the boosting-based algorithm, there is a strong dependence among individual learners. It is not suitable for parallel processing and has a low training efficiency. The bagging (bootstrap aggregating) ensemble method is based on bootstrap sampling [
37]. Suppose there are
training samples and
M individual learners; then,
N samples are randomly sampled from the original
samples to form a training set.
M training sets for
M individual learners can be obtained by repeating
M times sampling. Therefore, in the bagging-based method, there is no strong dependence between individual learners, which makes it suitable for parallel training. In this paper, the bagging-based ensemble method is utilized to form data diversity.
In ensemble learning, three combination strategies have been widely used, including averaging, voting, and learning-based strategies [
45]. For the regression problem, the first method is usually utilized, i.e., averaging the outputs of
M individual learners to obtain the final output. The second strategy is usually used for classification problems. The winner is the candidate with the maximum total number of votes [
46]. The learning-based method is different from the above two methods; it takes the outputs of
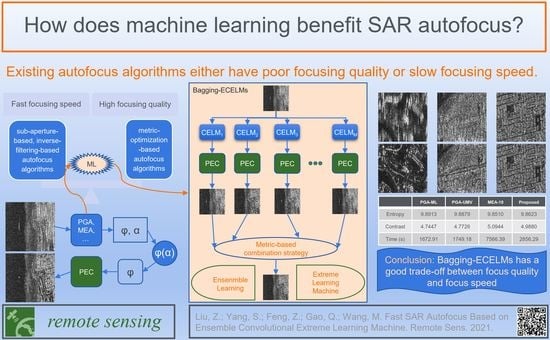
M individual learners as the inputs of a new learner, and the combination rules are automatically learned. To combine the results of multiple individual autofocus learners, we propose a metric-based combination strategy. In other words, the winner is the candidate with the optimal metric value (such as minimum-entropy or maximum-contrast. The framework of our proposed ensemble-learning-based autofocus algorithm is illustrated in
Figure 1, where “PEC” represents the phase error compensation module, which is formulated by Equation (
2).
In
Figure 1, there are
M homogeneous individual learners. Each learner is a Convolutional Extreme Learning Machine (CELM). Denote
as a defocused SAR image, where
are the number of pixels in azimuth and range, respectively. We can obtain
M estimated phase errror vectors
. These vectors are used to compensate for the defocused image
, and
M focused images
are obtained. Finally, our proposed metric-based combination strategy is applied to these images to obtain the final result. For example, if entropy is utilized as the metric, then the final focused image can be expressed as
Similarly, if contrast is utilized as the metric, then the final focused image can be expressed as
3.2. Convolutional Extreme Learning Machine
The original ELM is a three-layer neural network (input, hidden, output) designed for processing one-dimensional data. Denote
as the input vector, and
L as the number of neurons in the hidden layer. Let
represent the weight between input
and the
i-th neuron of hidden layer, and let
be the bias. The output of the
i-th hidden layer neuron can be expressed as
where
g is a nonlinear piecewise continuous function (activation function in traditional neural networks). The
L outputs of the
L hidden layer neurons can be represented as
, where
.
Denote
as the weight, ranging from the hidden layer to output layer;
K is the number of neurons in the output layer. For a classification problem,
K is the number of classes; for a regression problem,
K is the dimension of the vector to be regressed. The output of ELM can be formulated as
Suppose there is a training set with
N training samples:
, where
is the truth-value vector (for the classification problem,
is the one-hot class label vector). The hidden layer feature matrix of these
N samples is
. The classification or regression problem for ELM is to optimize
where
,
is the regularization factor,
is the truth-value matrix of the
N samples.
Equation (
19) can be solved by an iterative method, orthogonal projection method or singular value decomposition [
34,
47]. When
, Equation (
19) has the following closed-form solution [
32]
where
is an identity matrix. The process of solving
does not need iterative training, and it is very fast.
The original ELM can only deal with one-dimensional data. For two-dimensional or a higher dimensional input, it is usually flattened to a vector. This flattened operation destroys the original spatial structure of input data and leads ELMs to perform poorly in image-processing tasks. To overcome this problem, Huang et al. [
48] proposed a Local Receptive-Fields-Based Extreme Learning Machine (ELM-LRF). Differing from the traditional Convolutional Neural Network (CNN), the size and shape of the receptive field (convolutional kernel) of ELM-LRF can be generated according to the probability distribution. In addition, CNN uses a back-propagation algorithm to iteratively adjust the weights of all layers, while ELM-LRF has a closed-form solution.
In this paper, we propose a Convolutional Extreme Learning Machine (CELM) method for phase error estimation. The network structure of a single CELM is illustrated in
Figure 2. It contains a convolutional (Conv) layer, an Instance Normalization (IN) layer [
49], a Leaky Rectified Linear Unit (LeakyReLU) nonlinearity [
50], a Global Average Pooling (GAP) layer in range, a flattening layer, and an output layer. As mentioned above, in order to simplify the prediction problem, we use CELM to estimate the polynomial coefficients instead of phase errors. In
Figure 2,
K denotes polynomial coefficients and equals
, where
Q is the order of the polynomial.
The detailed configuration of CELM is shown in
Table 1. Suppose there is a complex SAR image of 256 pixels in both height and width. Denote
as the number of channels produced by convolution, and
n as the number of images in a batch. The output size of each layer in CELM is also displayed in
Table 1. As shown in
Figure 2 and
Table 1, there is only one convolutional layer in a CELM. The convolution stride is set to 1. In
Figure 2, the convolution kernel sizes for azimuth and range are 63 and 1, respectively.
Let
be convolution input, where
N is the number of inputs, and
are the height, width and channels of
, respectively. In this paper, the convolution kernels between channels do not share weights. Denote
as the weight matrix of the convolution kernels, where
are the height and width of the convolution kernel.
is the number of channels produced by the convolution. The convolution between
and
can be formulated as
where
, * represents the classic two-dimensional convolution operation, and
is the
-th channel of the
n-th image of
, and
. In this paper,
equals 2, since the defocused complex-valued SAR image is first converted into a two-channel image (real channel image and imaginary channel image) before being fed into CELM. As the phase distortion is in azimuth, we use azimuth convolution to extract features. Thus, the weight of the convolutional layer is a matrix with size
, where
is the number of channels produced by the convolution, 2 is the number of channels of the input image,
is the kernel size in azimuth.
The instance normalization of convolutional features
can be expressed as
where
are the channels, height, and width of
, respectively. The mean value
and standard variance
can be calculated by
After convolution and instance normalization, a LeakyReLU activation is applied to the normalized features
. Mathematically, the LeakyReLU function is expressed as
where
is the negative slope, set to 0.01 in this paper. Denote
as output features of the LeakyReLU nonlinearity. By appying the GAP operation to
in the range direction for dimension reduction, the features after pooling can be expressed as
where
is the features after the range GAP. Thus, each feature map is reduced to a feature vector. For an image,
feature vectors will be generated. These
feature vectors are flattened to a long feature vector
after the flatten operation. Combine the
N feature vectors
into a feature matrix
Similar to ELM-LRF, the convolution layer weights are fixed after random initialization. The weights
from hidden layer to the output (polynomial coefficients) can be solved by Equation (
20).
3.3. Model Training and Testing
In this paper, the classical bagging ensemble-learning method is applied to generate diverse data and train CELMs. The model trained with the bagging-based method is called Bagging-ECELMs. Suppose there is a training dataset
, and a validation dataset
, where
is the
n-th defocused image,
is the polynomial phase error coefficient vector of
, and
and
are the number of pixels in azimuth and range, respectively. Denote
M as the number of CELMs. In order to train the
M CELMs,
N samples are randomly selected from the training set
as the training samples of a single CELM, and
M training sets are obtained by repeating this process
M times. The validation dataset
was utilized to select the best factor
in Equation (
19). Assuming that there are
regularization factors are set in the experiment, then each CELM will be trained
times.
The training of a single CELM consists of two main steps: randomly initializing the input weights
(the weights of the convolution layer) and calculating the output weights (Equation (
20)). The input weights are randomly generated and then orthogonalized using singular value decomposition (SVD) [
48]. Assuming that there are
convolutional output channels, the convolution kernel size is
, where
is the kernel size in the azimuth and 1 is the kernel size in the range. Firstly, generate
convolution kernel weights
with standard Gaussian distribution. Secondly, combine these weights into a matrix
in order
Thirdly, orthogonalize the weight matrix with SVD, and obtain the orthogonalized weight . Finally, reshape the weights into a matrix with size to obtain the final input weights .
The pseudocode for training Bagging-ECELMs is summarized in Algorithm 1, where the entropy-based combination strategy is utilized (Equation (
15)). The testing process of Bagging-ECELMs model is very simple; see Algorithm 2 for details.
| Algorithm 1: Training CELMs based on bagging |
Input: The orignal training dataset , validation dataset , trade-off factor set , the number of CELMs M, the number of samples N used to train a single CELM. Output: The input weights and the output weights of the M CELMs.
- 1:
for to M do - 2:
set - 3:
randomly select N samples from set to form training set of the m-th CELM - 4:
randomly initialize the input weights of the M-th CELM - 5:
orthogonalize utilize SVD - 6:
for to do - 7:
compute feature matrix of using Equation ( 26) - 8:
compute output weights using Equation ( 20) - 9:
compute feature matrix of using Equation ( 26) - 10:
compute the estimated phase error coefficients - 11:
compute the phase error vector using Equation ( 14) and focus each validation image using Equation ( 2) - 12:
compute the entropy s of all the focused images - 13:
if then - 14:
- 15:
- 16:
end if - 17:
end for - 18:
end for
|
| Algorithm 2: Testing CELMs |
- 1:
for to M do - 2:
set - 3:
compute feature matrix of using Equation ( 26) - 4:
compute the estimated phase error coefficients - 5:
compute the phase error using Equation ( 14) and focus using Equation ( 2) - 6:
compute the entropy s of the focused image - 7:
if then - 8:
- 9:
- 10:
end if - 11:
end for
|