3.1. Framework of the Method
The core ideas of the DIPNet are described as follows:
- (1)
A PAN band contains potential information in the MS bands. Low-frequency PAN information can reflect the main MS information. High-frequency PAN information can reflect the details in the PAN band.
- (2)
In this study, pansharpening is viewed as a PAN band-guided SR problem. High-frequency PAN information is added to ameliorate the SR-induced blurring problem.
- (3)
Multiple SR processes are required to obtain an MS image with the same spatial resolution in the PAN band. In conventional methods, single-scale fusion is inordinately simple, while features fused at multiple scales have limited information content. Multiscale high- and low-frequency deep PAN and MS features can be combined to better describe the mapping relationship between PAN bands and MS bands and to achieve higher-accuracy pansharpening.
- (4)
A multiscale auxiliary encoder with detailed PAN information and potential MS information in the PAN band is used to further reconstruct spatial information for the MS image.
For clarity,
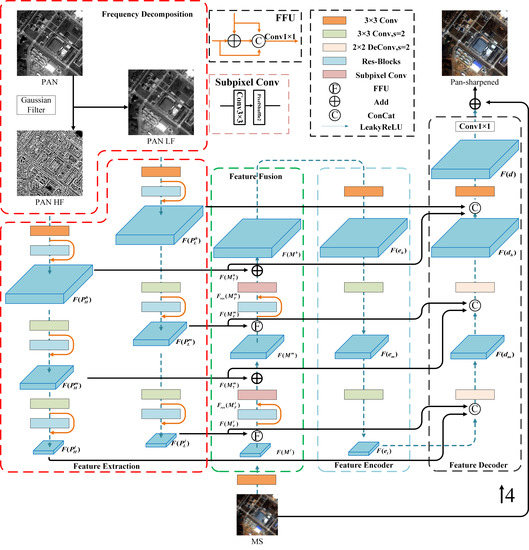
Figure 1 shows the workflow of our proposed work.
Figure 2 shows the network architecture designed in this study based on the abovementioned ideas.
To facilitate the description of the problem, let h and l be the spatial resolutions of the PAN image P and the MS image M, respectively. To ensure a clear discussion, the PAN image and MS image are denoted and , respectively. Pansharpening fuses these two images into an MS image with a spatial resolution of h. DIPNet involves four main steps:
(1) Frequency decomposition. In this step,
is decomposed into a high-pass component
and a low-pass component
.
reflects the high-frequency details (e.g., boundaries) of
.
reflects the complete spectral features (e.g., color features in a relatively large local area) of
. Frequency spectrum decomposition is achieved by Gaussian filtering. First, a Gaussian filter matrix with a window size of
is established. Second,
is filtered, and the result is treated as
. The difference between
and
is treated as
.
(2) Feature Extraction. Features are extracted from and using a 3 × 3 convolution operation followed by the ResNet module. Features and , each with a spatial resolution of h and a total of K channels, are thus obtained. In addition, features are extracted from using a 3 × 3 convolution operation. MS image features with a total of K channels and a resolution of l are also obtained.
In many cases, the spatial-resolution multiples (e.g., two, four, or eight iterations) vary between a PAN image and MS image. In each convolutional downsampling operation, the output feature size is half the input feature size. The number of downsampling iterations required to downsample the PAN image to the spatial resolution in the MS bands also varies. For ease of the description of the problem, let m be the intermediate resolution. For example, when the resolution ratio of an MS image to a PAN image is 4, l is 4, m is 2, and h is 1; when the resolution ratio of an MS image to a PAN image is 6, l is 6, m is 2, and h is 1. This paper discusses a situation in which the resolution ratio of an MS image to a PAN image is 4, which is suitable for most high-resolution satellite images.
and are downsampled by a 3 × 3 convolution operation with a step size of 2. Features are further extracted using the ResNet module. A high-pass component and a low-pass component, each with a spatial resolution of m, are thus obtained; they are denoted as and , respectively. Similarly, a high-pass component and a low-pass component, each with a spatial resolution of l, can be obtained; they are denoted as and , respectively.
From this process, a low-frequency PAN information feature group
and a high-frequency PAN information feature group
are obtained:
(3) Feature Fusion (FF). and are fused using an FFU. Features with a resolution of m are obtained by SR and subsequently added to pixel by pixel. This process is repeated, and ultimately, MS features with a resolution of h are obtained.
In this process, MS features are fused with low- and high-frequency PAN features at multiple scales. Thus, progressively fused MS features have more information content than features extracted from an interpolation-upscaled MS image.
(4) Image Reconstruction. An autoencoder is used to reconstruct the structure based on , , and (fused features obtained by FF-based SR). A PAN image with an enhanced spatial resolution is thus obtained. In this process, multiscale PAN features are injected into the decoder to further increase the information content of the MS image.
Regarding the network activation function, a leaky rectified linear unit with a parameter of 0.2 is set as the activation function for all the convolutional layers, except for the ResNet module and the subpixel and output convolutional layers for SR.
The following section introduces an FF-based SR module and image reconstruction module into which high- and low-frequency PAN information is injected.
3.2. FF-Based SR Module (Step 3)
Prior to SR, the FFU is used to fuse
and
in the following manner:
where
© represents an operation that connects feature images in series, ⊕ denotes an operation that adds feature images pixel by pixel,
is a convolution function with a convolution kernel size of 1, and
is the fused MS features (the subscript F indicates fused features). The FFU produces combined features with a total of
channels through a serial connection operation and subsequently performs a 1 × 1 convolution operation on the combined features to produce fused features with a total of
K channels. Thus, the extracted features are linearly fused by using rich per-added features.
Subsequently, the ResNet module is used to extract features from
:
where
represents the extraction operations by a total of
ResNet modules. The input features
are added for residual learning. Thus,
-based deep features
are obtained. For the extraction of PAN features in Step 2, the residual module similarly consists of a total of
ResNet modules.
Subpixel convolution [
26] is an upsampling method based on conventional convolution and pixel arrangement in feature images and can be used to achieve image SR. Let
r be the upscaling factor and
(
c,
h, and
w are the number of channels, height, and width, respectively) be the size of the initial input feature image
. First, through convolution operations on
, a total of
convolution kernels is extracted, and an output feature image with a size of
(i.e., a total of
vectors each with a length of
) is obtained. Second, all the vectors, each with a length of
, are arranged into a
pixel matrix. Thus, a feature image with a size of
is obtained. As the current resolution of this image is
m, it is denoted by
.
In conventional image SR, due to a lack of sufficient information for predicting the postupscaling pixel values, the post-SR image lacks detailed spatial features, i.e., the post-SR image is blurry. To address this problem, high-frequency features are fused to sharpen the blurry areas. The previously obtained
and the high-frequency information image
of the corresponding size extracted by convolution operations are added to restore a feature image that has become blurry after upscaling (i.e.,
), as shown in the following equation:
Based on these steps, the resolution of the MS image features is improved from l to m.
Similarly, the image features can be improved from m to h. Ultimately, fused MS and PAN image features are obtained.
3.3. Image Reconstruction Module into Which High- and Low-Frequency PAN Information Is Injected (Step 4)
A convolutional autoencoder can effectively encode an image to produce high-dimensional coded information and decode deep information by reversing the encoding process to reconstruct the input image. Thus, an autoencoder is employed to reconstruct the image based on
:
where
E represents a three-layer convolutional encoding operation (the first layer is a convolutional operation with a step size of 1 performed to produce coded features with a total of
channels and a resolution of
h; the last two layers are convolutional operations with a step size of 2 performed to produce coded features with a total of
channels and a resolution of
m and coded features with a total of
channels and a resolution of
l), and
,
, and
are coded features with scales of
h,
m, and
l, respectively.
Conventional convolution operations produce feature images with specific sizes based on the convolution kernel size, weight, and step size of the sliding window. Generally, convolution operations reduce the feature size. To preserve the feature size, it is possible to fill numerical values at the boundaries of the feature image.
The encoder applied in this study encodes each feature image by taking advantage of the properties of convolution to recover multiscale feature information and thus facilitate the injection of multiscale PAN features.
To utilize important multiscale PAN information, the high-frequency PAN information feature group
and low-frequency PAN information feature group
are injected into the features that require decoding through the decoder architecture as follows:
where
© represents an operation that connects feature images in a series based on the number of channels, and
represents a deconvolution operation, which is the reverse process of convolution and can upscale and output feature images with specific numbers of channels. Both
and
are 2 × 2 deconvolution operations with a step size of 2;
represents a conventional 3 × 3 convolution operation; and
,
, and
are fused high-frequency features, fused low-frequency features, and fused coded features, respectively, with resolutions of
l,
m, and
h and
,
, and
channels, respectively. The decoder used in this study upscales and decodes coded features by taking advantage of the properties of deconvolution.
is converted by a 1 × 1 convolution operation to the number of channels required for the MS image, to which the upsampled MS image
is added. Thus, a high-resolution MS image
is obtained, as shown here: