SFRS-Net: A Cloud-Detection Method Based on Deep Convolutional Neural Networks for GF-1 Remote-Sensing Images
Abstract
:1. Introduction
2. Methods
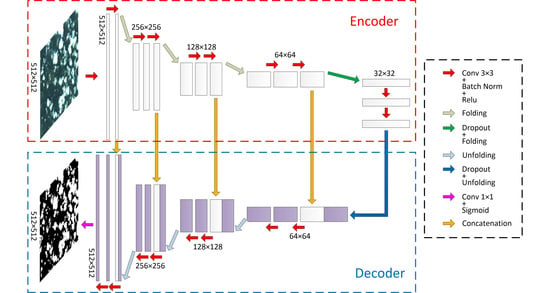
2.1. The SFRS-Net Architecture
2.1.1. Traditional Layers
2.1.2. Folding Layer and Unfolding Layer
2.2. Data Preprocessing
2.3. Implementation and Training
3. Results
3.1. Dataset
3.2. Evaluation Criteria
3.3. Validity of the Folding–Unfolding Method
3.4. Comparative Experiment of Different Bands
3.5. Comparative Experiment of Different Methods
4. Discussion
4.1. The Effectiveness of the Convolutional Network
4.2. The Effectiveness of the Folding–Unfolding Operation
4.3. Error Sources of the Proposed Method
4.4. Influencing Factors of the Proposed Method
4.5. Research and Application of the Proposed Method in the Future
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.; Zheng, H.; Han, C.; Wang, H.; Miao, M. Onboard spectral and spatial cloud detection for hyperspectral remote sensing images. Remote Sens. 2018, 10, 152. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zheng, H.; Han, C.; Wang, H.; Zheng, W. Cloud detection of superview-1 remote sensing images based on genetic reinforcement learning. Remote Sens. 2020, 12, 3190. [Google Scholar] [CrossRef]
- Jia, K.; Liang, S.; Gu, X.; Baret, F.; Wei, X.; Wang, X.; Yao, Y.; Yang, L.; Li, Y. Fractional vegetation cover estimation algorithm for Chinese GF-1 wide field view data. Remote Sens. Environ. 2016, 177, 184–191. [Google Scholar] [CrossRef]
- Mercury, M.; Green, R.; Hook, S.; Oaida, B.; Wu, W.; Gunderson, A.; Chodas, M. Global cloud cover for assessment of optical satellite observation opportunities: A HyspIRI case study. Remote Sens. Environ. 2012, 126, 62–71. [Google Scholar] [CrossRef]
- Shi, T.; Xu, Q.; Zou, Z.; Shi, Z. Automatic Raft Labeling for Remote Sensing Images via Dual-Scale Homogeneous Convolutional Neural Network. Remote Sens. 2018, 10, 1130. [Google Scholar] [CrossRef] [Green Version]
- Rossow, W.; Duenas, E. The International Satellite Cloud Climatology Project (ISCCP) Web site—An online resource for research. Bull. Am. Meteorol. Soc. 2016, 85, 167–172. [Google Scholar] [CrossRef]
- Zhang, Y.; Rossow, W.B.; Lacis, A.A.; Oinas, V.; Mishchenko, M.I. Calculation of radiative fluxes from the surface to top of atmosphere based on ISCCP and other global data sets: Refinements of the radiative transfer model and the input data. J. Geophys. Res. 2004, 109, 19105. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in Landsat imagery. Remote Sens. Environ. 2006, 106, 375–386. [Google Scholar] [CrossRef]
- Shahbaz, M.; Lean, H.H. Does financial development increase energy consumption? The role of industrialization and urbanization in Tunisia. Energy Policy 2012, 40, 473–479. [Google Scholar] [CrossRef] [Green Version]
- Superczynski, S.D.; Christopher, S.A. Exploring land use and land cover effects on air quality in Central Alabama using GIS and remote sensing. Remote Sens. 2011, 3, 2552. [Google Scholar] [CrossRef] [Green Version]
- Dong, Q.; Yue, C. Image Fusion and Quality Assessment of GF-1. For. Inventory Planning 2016, 41, 1–5. [Google Scholar] [CrossRef]
- Kotarba, A.Z. Evaluation of ISCCP cloud amount with MODIS observations. Atmos. Res. 2015, 153, 310–317. [Google Scholar] [CrossRef]
- Wang, B.; Ono, A.; Muramatsu, K. Automated detection and removal of clouds and their shadows from Landsat tm images. Ice Trans. Inf. Syst. 1999, 82, 453–460. [Google Scholar] [CrossRef]
- Udelhoven, T.; Frantz, D.; Schmidt, M. Enhancing the detectability of clouds and their shadows in multitemporal dryland Landsat imagery: Extending Fmask. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1242–1246. [Google Scholar] [CrossRef]
- Xiong, Q.; Wang, Y.; Liu, D.; Ye, S.; Zhang, X. A cloud detection approach based on hybrid multispectral features with dynamic thresholds for GF-1 remote sensing images. Remote Sens. 2020, 12, 450. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 39, 640–651. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask r-cnn. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 386–397. [Google Scholar] [CrossRef]
- Xue, Q.; Guan, L. A Cloud Detection Method Combining ATMS Measurements and CrIS Hyperspectral Infrared Data at Double Bands. In Proceedings of the 2019 International Conference on Meteorology Observations (ICMO), Chengdu, China, 28–31 December 2019. [Google Scholar] [CrossRef]
- Vittorio, A.; Emery, W.J. An automated, dynamic threshold cloud-masking algorithm for daytime AVHRR images over land. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1682–1694. [Google Scholar] [CrossRef]
- Liu, J. Improvement of dynamic threshold value extraction technic in fy-2 cloud detection. J. Infrared Millim. Waves 2010, 29, 288–292. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, Q.; Guo, N. The study of cloud detection with multi-channel data of satellite. Chin. J. Atmos. Sci. 2007, 31, 119–128. [Google Scholar] [CrossRef]
- Reynolds, D.W.; Haar, T.H.V. A bi-spectral method for cloud parameter determination. Mon. Weather. Rev. 1977, 105, 446–457. [Google Scholar] [CrossRef] [Green Version]
- Saunders, R.W.; Kriebel, K.T. An improved method for detecting clear sky and cloudy radiances from AVHRR data. Int. J. Remote Sens. 1988, 9, 123–150. [Google Scholar] [CrossRef]
- Irish, R.R.; Barker, J.L.; Goward, S.N.; Arvidson, T. Characterization of the Landsat-7 ETM+ automated cloud-cover assessment (ACCA) algorithm. Photogramm. Eng. Remote Sens. 2006, 72, 1179–1188. [Google Scholar] [CrossRef]
- Irish, R.R. Landsat 7 automatic cloud cover assessment. In Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VI; Shen, S.S., Descour, M.R., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2000; Volume 4049, pp. 348–356. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Qiu, S.; Zhu, Z.; He, B. Fmask 4.0: Improved cloud and cloud shadow detection in Landsats 4–8 and Sentinel-2 imagery. Remote Sens. Environ. 2019, 231, 111205. [Google Scholar] [CrossRef]
- Cai, Y.; Fu, D. Cloud recognition method and software design based on texture features of satellite remote sensing images. Trans. Atmos. Sci. 1999, 22, 416–422. [Google Scholar] [CrossRef]
- Welch, R.M.; Sengupta, S.K.; Chen, D.W. Cloud field classification based upon high-spatial resolution textural feature, 1.Gray-level co-occurrence matrix approach. J. Geophys. Res. 1988, 93, 12663–12681. [Google Scholar] [CrossRef]
- Tian, P.; Guang, Q.; Liu, X. Cloud detection from visual band of satellite image based on variance of fractal dimension. J. Syst. Eng. Electron. 2019, 30, 485–491. [Google Scholar] [CrossRef]
- Tan, Y.; Ji, Q.; Ren, F. Real-time cloud detection in high resolution images using Maximum Response Filter and Principle Component Analysis. In Proceedings of the IGARSS 2016—2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 6537–6540. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef] [Green Version]
- Bai, T.; Li, D.; Sun, K.; Chen, Y.; Li, W. Cloud detection for high-resolution satellite imagery using machine learning and multi-feature fusion. Remote Sens. 2016, 8, 715. [Google Scholar] [CrossRef] [Green Version]
- Tan, K.; Zhang, Y.; Tong, X. Cloud extraction from Chinese high resolution satellite imagery by probabilistic latent semantic analysis and object-based machine learning. Remote Sens. 2016, 8, 963. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Chova, L.; Camps-Valls, G.; Amoros-Lopez, J.; Guanter, L.; Alonso, L.; Calpe, J.; Moreno, J. New cloud detection algorithm for multispectral and hyperspectral images: Application to ENVISAT/MERIS and PROBA/CHRIS sensors. In Proceedings of the 2006 IEEE International Geoscience and Remote Sensing Symposium, Denver, CO, USA, 31 July–4 August 2006; pp. 2746–2749. [Google Scholar] [CrossRef]
- Yu, W.; Cao, X.; Xu, L.; Bencherkei, M. Automatic cloud detection for remote sensing image. Chin. J. Sci. Instrum. 2006, 27, 2184–2186. [Google Scholar] [CrossRef]
- Wieland, M.; Li, Y.; Martinis, S. Multi-sensor cloud and cloud shadow segmentation with a convolutional neural network. Remote Sens. Environ. 2019, 230, 111203. [Google Scholar] [CrossRef]
- Chen, N.; Li, W.; Gatebe, C.; Tanikawa, T.; Hori, M.; Shimada, R.; Aoki, T.; Stamnes, K. New neural network cloud mask algorithm based on radiative transfer simulations. Remote Sens. Environ. 2018, 219, 62–71. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.; Huang, W.; Li, Z.; Sun, L.; Zhu, X.; Yuan, Q.; Liu, L.; Cribb, M. Cloud detection for landsat imagery by combining the random forest and superpixels extracted via energy-driven sampling segmentation approaches. Remote Sens. Environ. 2020, 248, 112005. [Google Scholar] [CrossRef]
- Fu, H.; Shen, Y.; Liu, J.; He, G.; Chen, J.; Liu, P.; Qian, J.; Li, J. Cloud detection for FY meteorology satellite based on ensemble thresholds and random forests approach. Remote Sens. 2019, 11, 44. [Google Scholar] [CrossRef] [Green Version]
- Joshi, P.P.; Wynne, R.H.; Thomas, V.A. Cloud detection algorithm using SVM with SWIR2 and tasseled cap applied to Landsat 8. Int. J. Appl. Earth Obs. Geoinform. 2019, 82, 101898. [Google Scholar] [CrossRef]
- Li, P.; Dong, L.; Xiao, H.; Xu, M. A cloud image detection method based on SVM vector machine. Neurocomputing 2015, 169, 34–42. [Google Scholar] [CrossRef]
- Ishida, H.; Oishi, Y.; Morita, K.; Moriwaki, K.; Nakajima, T.Y. Development of a support vector machine based cloud detection method for MODIS with the adjustability to various conditions. Remote Sens. Environ. 2018, 205, 390–407. [Google Scholar] [CrossRef]
- Xie, F.; Shi, M.; Shi, Z.; Yin, J.; Zhao, D. Multilevel cloud detection in remote sensing images based on deep learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3631–3640. [Google Scholar] [CrossRef]
- Chai, D.; Newsam, S.; Zhang, H.K.; Qiu, Y.; Huang, J. Cloud and cloud shadow detection in Landsat imagery based on deep convolutional neural networks. Remote Sens. Environ. 2019, 225, 307–316. [Google Scholar] [CrossRef]
- Yang, J.; Guo, J.; Yue, H.; Liu, Z.; Hu, H.; Li, K. CDnet: CNN-based cloud detection for remote sensing imagery. IEEE Trans. Geosci. Remote Sens 2019, 57, 8. [Google Scholar] [CrossRef]
- Guo, J.; Yang, J.; Yue, H.; Tan, H.; Li, K. CDnetv2: CNN-based cloud detection for remote sensing imagery with cloud-snow coexistence. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1. [Google Scholar] [CrossRef]
- Mateo-García, G.; Laparra, V.; López-Puigdollers, D.; Gómez-Chova, L. Transferring deep learning models for cloud detection between Landsat-8 and Proba-V. ISPRS J. Photogramm. Remote Sens. 2020, 160, 1–17. [Google Scholar] [CrossRef]
- Mendili, L.E.; Puissant, A.; Chougrad, M.; Sebari, I. Towards a Multi-Temporal Deep Learning Approach for Mapping Urban Fabric Using Sentinel 2 Images. Remote Sens. 2020, 12, 423. [Google Scholar] [CrossRef] [Green Version]
- Jeppesen, J.H.; Jacobsen, R.H.; Inceoglu, F.; Toftegaard, T.S. A cloud detection algorithm for satellite imagery based on deep learning. Remote Sens. Environ. 2019, 229, 247–259. [Google Scholar] [CrossRef]
- Li, Z.; Shen, H.; Cheng, Q.; Liu, Y.; You, S.; He, Z. Deep learning based cloud detection for medium and high resolution remote sensing images of different sensors. ISPRS J. Photogramm. Remote Sens. 2019, 150, 197–212. [Google Scholar] [CrossRef] [Green Version]
- Ian, G.; Yoshua, B.; Aaron, C. Deep Learning; Posts & Telecom Press: Beijing, China, 2017; p. 76. [Google Scholar]
- Ning, J.; Liu, J.; Kuang, W.; Xu, X.; Zhang, S.; Yan, C.; Li, R.; Wu, S.; Hu, Y.; Du, G.; et al. Spatiotemporal patterns and characteristics of land-use change in china during 2010–2015. J. Geogr. Sci. 2018, 28, 547–562. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9. [Google Scholar] [CrossRef]













| Image (512 × 512) | |||
|---|---|---|---|
| Training | Validation | Test | |
| Amount | 7441 | 1063 | 2126 |
| Percentage | 70% | 10% | 20% |
| Spectral Band No. | Spectral Name | Spectral Range (μm) | Spatial Resolution (m) |
|---|---|---|---|
| Band1 | Blue | 0.45–0.52 | 8 |
| Band2 | Green | 0.52–0.59 | 8 |
| Band3 | Red | 0.63–0.69 | 8 |
| Band4 | Near Infrared(NIR) | 0.77–0.89 | 8 |
| Precision% | Recall% | FPR% | OA% | |
|---|---|---|---|---|
| Pooling | 96.74 | 95.80 | 3.95 | 95.91 |
| Folding–unfolding | 97.17 | 97.35 | 3.47 | 96.98 |
| B | G | R | NIR | RGB | VNIR | |
|---|---|---|---|---|---|---|
| Precision% | 94.38 | 93.80 | 95.79 | 94.17 | 97.13 | 97.17 |
| Recall% | 92.84 | 93.15 | 91.80 | 92.63 | 97.29 | 97.35 |
| FPR% | 6.76 | 7.52 | 4.93 | 7.01 | 3.51 | 3.47 |
| OA% | 93.02 | 92.85 | 93.27 | 92.79 | 96.93 | 96.98 |
| Precision% | Recall% | FPR% | OA% | |
|---|---|---|---|---|
| Additional image | 97.05 | 97.08 | 3.61 | 96.77 |
| Method | Evaluation Metrics | Vegetation | Mountain | Water | City | Desert | Snow/Ice | Entire Test Set |
|---|---|---|---|---|---|---|---|---|
| The spectral threshold method | Precision% | 96.71 | 95.94 | 97.09 | 94.68 | 85.86 | 78.72 | 92.36 |
| Recall% | 94.94 | 96.42 | 92.71 | 93.37 | 89.30 | 81.99 | 89.37 | |
| FPR% | 4.84 | 5.75 | 4.63 | 6.82 | 12.03 | 20.05 | 9.03 | |
| OA% | 95.03 | 95.52 | 93.71 | 93.29 | 88.57 | 80.92 | 90.09 | |
| Deeplab-V3+ | Precision% | 97.95 | 97.78 | 97.32 | 96.37 | 92.61 | 89.81 | 96.07 |
| Recall% | 98.41 | 97.98 | 95.56 | 96.23 | 95.08 | 93.13 | 96.23 | |
| FPR% | 3.09 | 3.13 | 4.39 | 4.71 | 6.21 | 9.56 | 4.81 | |
| OA% | 97.81 | 97.52 | 95.58 | 95.82 | 94.37 | 91.72 | 95.76 | |
| The proposed method | Precision% | 98.68 | 98.78 | 97.45 | 96.89 | 93.97 | 91.35 | 97.17 |
| Recall% | 98.50 | 98.81 | 96.99 | 97.22 | 95.75 | 93.74 | 97.35 | |
| FPR% | 1.98 | 1.72 | 4.23 | 4.05 | 5.12 | 8.03 | 3.47 | |
| OA% | 98.31 | 98.59 | 96.53 | 96.67 | 95.27 | 92.81 | 96.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zheng, H.; Han, C.; Zheng, W.; Chen, H.; Jing, Y.; Dong, K. SFRS-Net: A Cloud-Detection Method Based on Deep Convolutional Neural Networks for GF-1 Remote-Sensing Images. Remote Sens. 2021, 13, 2910. https://doi.org/10.3390/rs13152910
Li X, Zheng H, Han C, Zheng W, Chen H, Jing Y, Dong K. SFRS-Net: A Cloud-Detection Method Based on Deep Convolutional Neural Networks for GF-1 Remote-Sensing Images. Remote Sensing. 2021; 13(15):2910. https://doi.org/10.3390/rs13152910
Chicago/Turabian StyleLi, Xiaolong, Hong Zheng, Chuanzhao Han, Wentao Zheng, Hao Chen, Ying Jing, and Kaihan Dong. 2021. "SFRS-Net: A Cloud-Detection Method Based on Deep Convolutional Neural Networks for GF-1 Remote-Sensing Images" Remote Sensing 13, no. 15: 2910. https://doi.org/10.3390/rs13152910
APA StyleLi, X., Zheng, H., Han, C., Zheng, W., Chen, H., Jing, Y., & Dong, K. (2021). SFRS-Net: A Cloud-Detection Method Based on Deep Convolutional Neural Networks for GF-1 Remote-Sensing Images. Remote Sensing, 13(15), 2910. https://doi.org/10.3390/rs13152910