Deposits’ Morphology of the 2018 Hokkaido Iburi-Tobu Earthquake Mass Movements from LiDAR & Aerial Photographs
Abstract
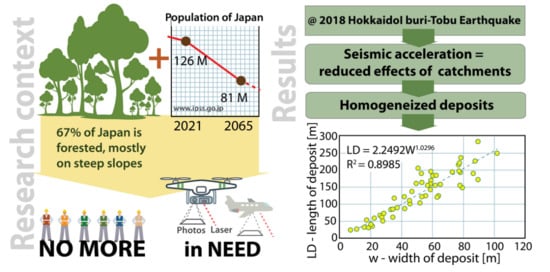
:1. Introduction
1.1. The 2018 Hokkaido Iburi-Tobu (HIT) Earthquake and the Coseismic Mass-Movements
- (1)
- to contribute to existing databases of the morphology of mass-movement deposits and how they relate to the watershed morphometry they flow in (e.g., ENTLI in Hong-Kong, or in Taiwan after the Typhoon Morakot) [12];
- (2)
- to provide an insight into the 3D geometrical relationships of the deposits in the area impacted by the HIT-earthquake, as existing work has been so far focused on the spatial distribution of the events and the 2D characterization of the mass-movement deposits.
1.2. The Mapping of Mass-Movements from Aerial Remote-Sensing Platforms
1.3. Empirical Relationships for Mass-Movements
2. Methodology
2.1. Data Acquisition: Information Retrieval from Lidar and Aerial Photographs Using GIS
2.2. Empirical Analysis
3. Results
3.1. The Geometry of the Deposits on Pseudo-Horizontal Surfaces
3.2. Surface—Volume Relations of the Deposits
3.3. The Fahrböschung for “Open-Slopes” and “Valley-Confined” Flows
4. Discussion
4.1. Result Summary
4.2. The Hokkaido Iburi-Tobu Earthquake Landslides Were Extremely Mobile
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| C’ | effective cohesion |
| D | Deposit volume calculated from the LiDAR data assuming a flat underlying layer and no erosion [m3] |
| F | fahrböschung [no unit] |
| k | the factor relating volume to area [1/m] |
| LD | Length of the deposit [m] |
| S | Surface of the deposit calculated from the LiDAR and aerial photographs [m2] |
| SF | Ratio of the width to the Length of the deposit [no unit] |
| T | One of the scalar used in Takahashi’s equations relating debris flow volume to area [1/m] |
| W | Maximum width of the deposit measured near or at the centre [m] |
| τf | Shear stress along the failure plane |
| σ | is the total stress in Terzaghi’s principle |
| σ’ | is the effective stress |
| σf | total normal stress along the plane of failure |
| φ’ | effective angle of internal friction |
| u | pore water pressure in Terzaghi’s principle |
| uw | the stress due to the water in the grain interspace. |
References
- Cheung, R.W.M. Landslide risk management in Hong Kong. Landslides 2021, 1–17. [Google Scholar] [CrossRef]
- Wong, H.N.; Ko, F.W.Y. Landslide risk assessment—Application and Practice. In Geo-Report 195; The Government of Hong Kong Special Administration Region: Hongkong, China, 2006; 279p. [Google Scholar]
- Gao, L.; Zhang, L.M.; Cheung, R.W.M. Relationships between natural terrain landslide magnitudes and triggering rainfall based on a large landslide inventory in Hong Kong. Landslides 2017, 15, 727–740. [Google Scholar] [CrossRef]
- Osanai, N.; Yamada, T.; Hayashi, S.; Katsura, S.; Furuichi, T.; Yanai, S.; Murakami, Y.; Miyazaki, T.; Tanioka, Y.; Takiguchi, S.; et al. Characteristics of landslides caused by the 2018 Hokkaido Eastern Iburi Earthquake. Landslides 2019, 16, 1517–1528. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, Y.; Feng, Q.; Guo, F.; Zhao, X.; Ji, F.; Liu, J.; Ming, W. Preliminary analysis of some characteristics of coseismic landslides induced by the Hokkaido Iburi-Tobu earthquake (5 September 2018). Catena 2020, 189, 104502. [Google Scholar] [CrossRef]
- Ohzono, M.; Takahashi, R.; Ito, C. Spatiotemporal crustal strain distribution around the Ishikari-Teichi-Toen fault zone estimated from global navigation satellite system data. Earth Planets Space 2019, 71, 50. [Google Scholar] [CrossRef]
- Kobayashi, T.; Hayashi, K.; Yarai, H. Geodetically estimated location and geometry of the fault plane involved in the 2018 Hokkaido Eastern Iburi earthquake. Earth Planets Space 2019, 71, 62. [Google Scholar] [CrossRef]
- Kubo, H.; Iwaki, A.; Suzuki, W.; Aoi, S.; Sekiguchi, H. Estimation of the source process and forward simulation of long-period ground motion of the 2018 Hokkaido Eastern Iburi, Japan, earthquake. Earth Planets Space 2020, 72, 20. [Google Scholar] [CrossRef] [Green Version]
- Takai, N.; Shigefuji, M.; Horita, J.; Nomoto, S.; Maeda, T.; Ichiyanagi, M.; Takahashi, H.; Yamanaka, H.; Chimoto, K.; Tsuno, S.; et al. Cause of destructive strong ground motion within 1–2 s in Mukawa town during the 2018 Mw 66 Hokkaido eastern Iburi earthquake. Earth Planets Space 2019, 71, 67. [Google Scholar] [CrossRef] [Green Version]
- Yamagishi, H.; Yamazaki, F. Landslides by the 2018 Hokkaido Iburi-tobu earthquake on setpember 6. Landslides 2018, 15, 2521–2524. [Google Scholar] [CrossRef] [Green Version]
- Chang, M.; Zhou, Y.; Zhou, C.; Hales, T.C. Coseismic landslides induced by the 2018 Mw 6.6 Iburi, Japan, Earthquake: Spatial distribution, key factors weight and susceptibility regionalization. Landslides 2021, 18, 755–772. [Google Scholar] [CrossRef]
- Tsai, T.-T.; Tsai, K.-J.; Shieh, C.-L. Large Scale Landslide Database System Established for the Reservoirs in Southern Taiwan. In Proceedings of the 19th EGU General Assembly, Vienna, Austria, 23–28 April 2017; p. 13505. [Google Scholar]
- Calista, M.; Miccadei, E.; Piacentini, T.; Sciarra, N. Morphostructural, Meteorological and Seismic Factors Controlling Landlsides in Weak Rocks: The Case Studies of Castelnuovo and Ponzano (North East Abruzzo, Central Italy). J. Geosci. 2019, 9, 122. [Google Scholar] [CrossRef] [Green Version]
- Pu, X.; Wan, L.; Wang, P. Initiation mechanism of mudflow-like loess landslide induced by the combined effect of earthquakes and rainfall. Nat. Hazards 2021, 105, 3079–3097. [Google Scholar] [CrossRef]
- Morelli, S.; Prazzi, V.; Frodella, W.; Fanti, R. Kinematic Reconstruction of a Deep-Seated Gravitational Slope Deformation by Geomophic Analyses. J. Geosci. 2018, 8, 26. [Google Scholar] [CrossRef] [Green Version]
- Agliardi, F.; Crosta, G.B.; Zanchi, A. Strutural constraints on deep-seated slope deformation kinematics. Eng. Geol. 2001, 59, 83–102. [Google Scholar] [CrossRef]
- Bovenga, F.; Nutricato, R.; Refice, A.; Wasowski, J. Application of multi-temporal differential interferometry to slope instability detection in urban/peri-urban areas. Eng. Geol. 2006, 88, 219–240. [Google Scholar] [CrossRef]
- Tomas, R.; Li, Z.; Lopez-Sanchez, J.M.; Liu, P.; Singleton, A. Using wavelet tools to analyse seasonal variations from InSAR time-series data: A case study of the Huangtupo landslide. Landslides 2016, 13, 437–450. [Google Scholar] [CrossRef] [Green Version]
- Gomez, C.; Allouis, T.; Lissak, C.; Hotta, N.; Shinohara, Y.; Hadmoko, D.S.; Vilimek, V.; Wassmer, P.; Lavigne, F.; Setiawan, A.; et al. High-resolution Point-Cloud for Landslides in the 21st Century: From Data Acquisition to New Processing Concepts. In Understanding and Reducing Landslide Disaster Risk, ICL Contribution to Landslide Disaster Risk Reduction; Arbanas, Ž., Bobrowsky, P.T., Konagai, K., Sassa, K., Takara, K., Eds.; Springer: Cham, Switzerland, 2021; pp. 199–213. [Google Scholar]
- Strozzi, T.; Ambrosi, C. SAR Interferometric Point Target Analysis and Interpretation of Aerial Photographs for Landslides Investigations in Ticino, southern Switzerland. In Proceedings of the ENVISAT Symposium, Montreux, Switzerland, 23–27 April 2007. [Google Scholar]
- Gomez, C.; Hayakawa, Y.; Obanawa, H. A study of Japanese landscapes using structure from motion derived DSMs and DEMs based on historical aerial photographs: New opportunities for vegetation monitoring and diachronic geomorphology. Geomorphology 2015, 242, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Koukouvelas, I.K.; Nikolakopoulos, K.G.; Zygouri, V.; Kyriou, A. Post-seismic monitoring of cliff mass wasting using an unmanned aerial vehicle and field data at Egremni, Lefkada Island, Greece. Geomorphology 2020, 367, 107306. [Google Scholar] [CrossRef]
- Clapuyt, F.; Vanacher, V.; Oost, K.V. Reproducibility of UAV-based earth topography reconstructions based on Structure-from-Motion algorithms. Geomoprhology 2016, 260, 4–15. [Google Scholar] [CrossRef]
- Mateos, R.M.; Azanon, J.M.; Roldan, F.J.; Notti, D.; Perez-Pena, V.; Galve, J.P.; Perez-Garcia, J.L.; Colomo, C.M.; Gomez-Lopez, J.M.; Montserrat, O.; et al. The combined use of PSInSAR and UAV photogrammetry techniques for the analysis of the kinematics of a coastal landslide affecting an urban area (SE Spain). Landslides 2017, 14, 743–754. [Google Scholar] [CrossRef]
- Peternal, T.; Kuemlj, S.; Ostir, K.; Komac, M. Monitoring the Potoska planina landslide (NW Slovenia) using UAV photogrammetry and tachymetric measurements. Landslides 2017, 14, 395–406. [Google Scholar] [CrossRef]
- Eker, R.; Aydin, A.; Hubl, J. Unmanned aerial vehicle (UAV)-based monitoring of a landslide: Gallenzerkogel landslide (Ybbs-Lower Austria) case study. Environ. Monit Assess. 2018, 190, 1–14. [Google Scholar] [CrossRef]
- Garcia-Pena, R.; Alcantara-Ayala, I. The use of UAVs for landslide disaster risk research and disaster risk management: A literature review. J. Mt. Sci. 2021, 18, 482–498. [Google Scholar] [CrossRef]
- Litoseliti, A.; Koukouvelas, I.K.; Nikolakopoulos, G.; Zygouri, V. An Event-Based Inventory Approach in Landslide Hazard Assessment: The Case of the Skolis Mountain, Northwest Peloponnese, Greece. ISPRS Int. J. Geo-Inf. 2020, 9, 457. [Google Scholar] [CrossRef]
- Hungr, O. Classification and terminology. In Debris-Flow Hazards and Related Phenomena; Jakob, M., Hungr, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 9–24. [Google Scholar]
- Scheidl, C.; Rickenmann, D. Empirical prediction of debris-flow mobility and deposition on fans. Earth Surf. Process. Landf. 2010, 35, 157–173. [Google Scholar] [CrossRef]
- Crosta, G.B.; Cucchiaro, S.; Frattini, P. Validation of semi-empirical relationships for the definition of debris-flow behavior in granular materials. In Debris-Flow Hazards Mitigation; Chen, C.L., Major, J.J., Eds.; Mill Press: Rotterdam, The Netherlands, 2003; pp. 821–831. [Google Scholar]
- Iverson, R.M.; Schilling, S.P.; Vallance, J.W. Objective delineation of lahar-inundation hazard zones. Geol. Soc. Am. Bull. 1998, 110, 972–984. [Google Scholar] [CrossRef]
- Corominas, J. The angle of reach as a mobility index for small and large landslides. Can. Geotech. J. 1996, 33, 260–271. [Google Scholar] [CrossRef]
- Rickenmann, D. Runout prediction methods. In Debris-Flow Hazards and Related Phenomena; Jakob, M., Hungr, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 305–324. [Google Scholar]
- Rickenmann, D. Empirical relationships for debris flows. Nat. Hazards 1999, 19, 47–77. [Google Scholar] [CrossRef]
- Takahashi, T. Debris Flow—Mechanics, Prediction and Countermeasures, 2nd ed.; CRC Press/Balkema: Boca Raton, FL, USA, 2014; 540p. [Google Scholar]
- Lagmay, A.M.F.; Escape, C.M.; Ybanez, A.A.; Suarez, J.K.; Cuaresma, G. Anatomy of the Naga City Landslide and Comparison with Historical Debris Avalanches and Analog Models. Front. Earth Sci. 2020, 8, 312. [Google Scholar] [CrossRef]
- Catane, S.; Veracruz, N.; Flora, J.; Go, C.; Enrera, R.; Santos, E. Mechanism of a low-angle translational block slide: Evidence from the September 2018 Naga landslide, Philippines. Landslides 2019, 16, 1709–1719. [Google Scholar] [CrossRef]
- Xing, A.; Wang, G.; Yin, Y.; Tang, C.; Xu, Z.; Li, W. Investigation and dynamic analysis of a catastrophic rock avalanche on September 23, 1991, Zhaotong, China. Landslides 2016, 13, 1035–1047. [Google Scholar] [CrossRef]
- Coombs, S.P.; Apostolov, A.; Take, W.A.; Benoit, J. Mobility of dry granular flows of varying collisional activity quantified by smart rock sensros. Can. Geotech. J. 2020, 57, 1484–1496. [Google Scholar] [CrossRef]
- Gomez, C.; Shinohara, Y.; Hotta, N.; Tsunetaka, H. In-flow Self-comminution of Debris-flow and Lahars: Fragmentation and Grinding Experiments for the Dacites from Unzen-Volcano. In Proceedings of the 10th Symposium of Sediment Hazards, Japan, 9 September 2020; pp. 127–132. [Google Scholar]
- Yamanouchi, T.; Murata, H. Brittle failure of a volcanic ash soil “Shirasu”. In Proceedings of the 8th International Conference on Soil Mechanics and Foundation Engineering, Moscow, Russia, 6–11 August 1973; Volume 1, pp. 495–500. [Google Scholar]
- Gonzalez de Vallejo, L.I.; Jimenez Salas, J.A.; Leguey Jiminez, S. Engineering geology of the tropical volcanic soils of La Laguna, Tenerife. Eng. Geol. 1981, 17, 1–17. [Google Scholar] [CrossRef]
- O’Rourke, T.D.; Crespo, E. Cemented volcanic soil. J. Geotech. 1988, 114, 1126–1147. [Google Scholar] [CrossRef]
- Zhang, X.J.; Chen, W.F. Stability analysis of slopes with general nonlinear failure criterion. Int. J. Numer. Anal. Methods Geomech. 1987, 11, 33–50. [Google Scholar] [CrossRef]
- Zhao, L.-H.; Cheng, X.; Dan, H.-C.; Tang, Z.-P.; Zhang, Y. Effect of the vertical earthquake component on permanent seismic displacement of soil slopes based on the nonlinear Mohr-Coulomb failure criterion. Soils Founds 2017, 57, 237–251. [Google Scholar] [CrossRef]
- Gomez, C.; Soltanzadeh, I. Boundary crossing and non-linear theory in earth-system sciences—A proof of concept based on tsunami and post-eruption scenarios on Java Island, Indonesia. Earth Surf. Process Landf. 2012, 37, 790–796. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez, C.; Hotta, N. Deposits’ Morphology of the 2018 Hokkaido Iburi-Tobu Earthquake Mass Movements from LiDAR & Aerial Photographs. Remote Sens. 2021, 13, 3421. https://doi.org/10.3390/rs13173421
Gomez C, Hotta N. Deposits’ Morphology of the 2018 Hokkaido Iburi-Tobu Earthquake Mass Movements from LiDAR & Aerial Photographs. Remote Sensing. 2021; 13(17):3421. https://doi.org/10.3390/rs13173421
Chicago/Turabian StyleGomez, Christopher, and Norifumi Hotta. 2021. "Deposits’ Morphology of the 2018 Hokkaido Iburi-Tobu Earthquake Mass Movements from LiDAR & Aerial Photographs" Remote Sensing 13, no. 17: 3421. https://doi.org/10.3390/rs13173421
APA StyleGomez, C., & Hotta, N. (2021). Deposits’ Morphology of the 2018 Hokkaido Iburi-Tobu Earthquake Mass Movements from LiDAR & Aerial Photographs. Remote Sensing, 13(17), 3421. https://doi.org/10.3390/rs13173421