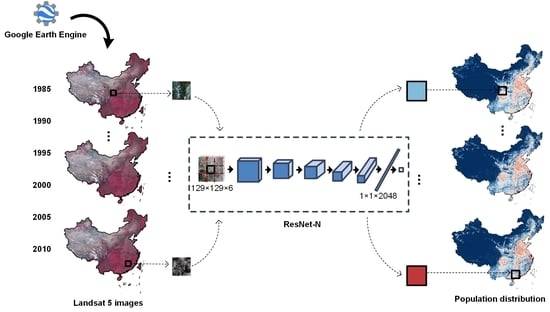
Mapping Multi-Temporal Population Distribution in China from 1985 to 2010 Using Landsat Images via Deep Learning

Abstract

Fine knowledge of the spatiotemporal distribution of the population is fundamental in a wide range of fields, including resource management, disaster response, public health, and urban planning. The United Nations’ Sustainable Development Goals also require the accurate and timely assessment of where people live to formulate, implement, and monitor sustainable development policies. However, due to the lack of appropriate auxiliary datasets and effective methodological frameworks, there are rarely continuous multi-temporal gridded population data over a long historical period to aid in our understanding of the spatiotemporal evolution of the population. In this study, we developed a framework integrating a ResNet-N deep learning architecture, considering neighborhood effects with a vast number of Landsat-5 images from Google Earth Engine for population mapping, to overcome both the data and methodology obstacles associated with rapid multi-temporal population mapping over a long historical period at a large scale. Using this proposed framework in China, we mapped fine-scale multi-temporal gridded population data (1 km × 1 km) of China for the 1985–2010 period with a 5-year interval. The produced multi-temporal population data were validated with available census data and achieved comparable performance. By analyzing the multi-temporal population grids, we revealed the spatiotemporal evolution of population distribution from 1985 to 2010 in China with the characteristic of concentration of the population in big cities and the contraction of small- and medium-sized cities. The framework proposed in this study demonstrates the feasibility of mapping multi-temporal gridded population distribution at a large scale over a long period in a timely and low-cost manner, which is particularly useful in low-income and data-poor areas.

1. Introduction

Understanding the spatiotemporal distribution of the population is fundamental in a wide range of fields, including resource management [1,2], disaster response [3,4,5,6], public health [7,8,9], and urban planning [10,11]. The United Nations’ Sustainable Development Goals (SDGs) also require the accurate and timely assessment of where people live to formulate, implement, and monitor sustainable development policies [12,13].

Census data released by an official body are authoritative and vital data about population distribution [14]. However, census data are based on administrative units; thus, they have several inherent limitations and are ill-suited to many spatial studies. Firstly, there is significant spatial heterogeneity in population distribution, which cannot be reflected by census data, which assumes a completely uniform distribution of the population within census units [15]. Secondly, the size of administrative units varies significantly in urban and rural areas, which results in the Modifiable Areal Unit Problem [16]. Thirdly, administrative boundaries may change over time and are seldom compatible with practical applications, making census data challenging to integrate with other spatial data sets, preventing interdisciplinary research and temporal dynamic analysis [17]. In order to overcome the limitations of census data, fine-grained gridded population data, which are spatially continuous, are produced to supplement census data [18,19].

Several approaches have been developed to produce fine-scale gridded population data in the past few decades, such as areal weighting [20], spatial interpolation [21,22,23], and dasymetric mapping [24,25,26,27,28,29,30,31,32]. Among them, dasymetric mapping technology [33], which uses fine-scale auxiliary variables and specific weighting schemes to re-allocate census counts to grid cells, is the most widely used and effective one [19]. Commonly adopted ancillary data include land use/cover data [34,35,36], nighttime light data [26,37], terrain data [38], and social sensing data (e.g., points-of-interest [39], mobile phone records [40], and social media data [41]). Multiple methods, including empirical rules [15], statistical models (e.g., linear regression [34] and geographically weighted regression [17]), and machine learning models (e.g., random forest [42], expectation-maximization [43], and neural network [44]), have been proposed to estimate the distribution weight of grid cells. Various gridded population data at regional and global scales have been produced and published using the methods mentioned above, including the Gridded Population of the World (GPW) [45], Global Human Settlement Population layer (GHS-POP) [46], Global Rural-Urban Mapping Project (GRUMP) [47], WorldPop [48], and LandScan [49].

The accuracy of gridded population data is determined by the quality of auxiliary data [19]. Numerous previous studies focused on integrating novel auxiliary variables related to population distribution to improve the quality of the produced population grids [15,50,51]. The thematic, spatial, and temporal accuracy of auxiliary data themselves is also crucial to the quality of the final gridded data [19]. For example, classification error in land use/land cover data will be propagated to the produced gridded population data. Furthermore, involving more auxiliary variables contributes more uncertainty to the final result [34]. In order to produce multi-temporal gridded population data, temporally explicit and consistent auxiliary data are essential, whose availability and sustainability are questionable, especially at a large scale, precluding the production of continuous multi-temporal data over a long historical period [34].

Remote sensing (RS) data (e.g., satellite imagery) that can capture the physical characteristics of the ground at low cost, broad coverages, and high spatiotemporal resolution are becoming increasingly available with improvements in imaging technology over time [36,52]. The physical characteristics of the ground and human activities interact with each other. Human activities can lead to distinct spatial landscapes, which inversely constrain how people live, produce, and travel, providing the possibility of consistent and sustainable population estimation with RS imagery as auxiliary data without the problems mentioned above [53]. However, the raw RS imagery is highly unstructured, and its association with population count is complex and nonlinear, making it challenging to construct a mapping from raw RS imagery to population count [54]. An emerging supervised deep learning approach, convolutional neural networks (CNN), which are capable of extracting the hidden hierarchical structures of RS images [55], have shown outstanding performance in obtaining knowledge from RS images in the domain of geography (e.g., land use classification [56], spatial interpolation [57], and poverty mapping [58]). Therefore, it is possible that CNN can form a mapping from RS imagery to population count.

A few studies have tried to estimate population counts from RS imagery directly. Doupe proposed the use of a VGG-like network to estimate population density in Tanzanian and Kenya from Landsat images and achieved remarkable performance and generalizability [54]. Robinson regarded the population estimation task as a classification problem and used a similar VGG-like network to classify RS image patches into 14 population density levels. They produced gridded population data for the United States in 2010, achieved high performance, and qualitatively explained the predictions in terms of the input RS imagery [59]. Xing proposed a Neighbor-ResNet architecture by embedding the neighbor knowledge into ResNet in order to estimate the volumes of human activity from Google imagery in 18 cities in China [53]. The attempts mentioned above verify the feasibility and superiority of integrating CNN and RS imagery for population mapping. However, the established models have not been used to map historical population distributions and understand their spatiotemporal evolution.

China is the world’s most populous developing country. Fine-scale population distribution data are crucial for China’s sustainable development [13]. Numerous gridded population data of China, with various spatial resolutions, have been developed [25,39]. A few studies have also used time-invariant and time-explicit auxiliary variables to produce multi-temporal gridded population distribution data [17,30,60]. However, due to the lack of appropriate auxiliary datasets and effective methodological frameworks, there are rarely continuous multi-temporal gridded population data for China over a long historical period to aid in our understanding of the spatiotemporal evolution of the population.

In this study, we developed a framework integrating a ResNet-N deep learning architecture with the consideration of neighborhood effects with a vast number of Landsat-5 images from Google Earth Engine (GEE) [61] for population mapping to overcome both the data and methodology obstacles of rapid multi-temporal population mapping over a long historical period at a large scale. Once the framework was constructed, we developed multi-temporal gridded population data with a 1 km resolution for China (excluding Taiwan, Hong Kong, and Macao) for the 1985–2010 period with a 5-year interval and analyzed its spatiotemporal evolution.

2. Materials and Methods

This study aimed to develop a framework integrating a deep learning model with Landsat-5 RS images from GEE to estimate population count. Once the framework is established, large-scale population mapping can be achieved only with easily accessible and regularly updatable RS imagery. Furthermore, we produce multi-temporal gridded population data (1 km × 1 km) of China for the 1985–2010 period with a 5-year interval and analyze the spatiotemporal evolution of the population distribution of China in this period. The flowchart of this study is illustrated in Figure 1, containing three main parts: (1) we collected ground-truth population count grid cells and corresponding Landsat-5 RS image patches as reference datasets for training, validating, and testing the developed deep learning model; (2) a ResNet-N architecture considering neighborhood effects was developed to establish the end-to-end mapping between population count and RS image patches; (3) based on the trained model, we estimated the gridded population count of China with corresponding Landsat-5 image patches from GEE as input from 1985 to 2010. Furthermore, the produced raw estimations were adjusted by available census data to acquire the final gridded population data. Finally, we validated the produced datasets and analyzed the spatiotemporal evolution of China’s population distribution.

2.1. Data Sources and Preprocessing

2.1.1. Ground-Truth Population Grid

In order to establish an end-to-end mapping between Landsat-5 RS image patches and population count by deep learning architecture, it is necessary to collect ground-truth population grid cells as training samples. However, the ground-truth population grid does not exist [19]. In this study, an alternative method (Figure 2) was utilized to collect the closest ground-truth population grid samples with a resolution of 1 km.

We obtained China’s 2010 population census data at the town level (level 4 administrative unit), the finest-scale census data publicly available, from China’s Sixth National Population Census. Towns are the fundamental administrative units in China, with relatively small jurisdiction areas, 58% of which are less than 100 km², so that the spatial heterogeneity of population distribution is tiny within towns. However, it is not adequate to use the average population density of towns as references due to heterogeneity within towns [62]. We obtained the WorldPop gridded population data [48] with a resolution of 1 km for China in 2010 to remedy this problem. The WorldPop data are produced by coupling a random forest algorithm with various auxiliary data to disaggregate county-level (level 3 administrative units) census data, recognized as some of the finest gridded population data to date [5]. In this study, we used WorldPop data in 2010 as a weighting layer to redistribute the total population count of each town to grid cells to account for the spatial heterogeneity within towns in part. Numerous towns are small in area. Therefore, this modified population map represents the closest ground-truth population grid that is available to use as training data. Finally, we sampled 100,000 grid cells from the ground-truth population grid weighted by the quality of grid cells to tradeoff the reliability and representativeness of the samples. The administrative areas of towns act as a data quality metric of grid cells [19]. Let $are{a}^k$ represent the area of the $k^{th}$ town; then, the weight of selecting a grid cell inside the $k^{th}$ town is given as $\frac{1}{are{a}^k}$. We discarded the grid cells with a population count of less than 10. It is unnecessary and intractable to distinguish the subtle change in population count via RS images in a 1 km² area [59]. The distribution of ground-truth population samples is heavily tailed, with kurtosis of 1312.41 and skewness of 26.31. To balance the dataset and ease the training of the deep learning model, the population count was logarithmized [53]. The collected samples were randomly divided into three groups: training (70%), validation (10%), and testing (20%). Figure 3 presents the spatial distribution of the collected population samples.

2.1.2. Landsat-5 RS Imagery

This study used RS images from Landsat-5 collected by the Thematic Mapper (TM) sensor, covering the 1985–2010 period [52]. The full Landsat-5 L1T-level surface reflectance archive [63] covering China with a cloud score of less than 60 was preprocessed and downloaded effortlessly from GEE, a cloud-based platform for processing petabyte-scale geospatial datasets [61]. The L1T-level products have undergone geometric, radiation, and atmospheric corrections and are ready for use [64,65]. After masking clouds and shadows using Landsat quality flag information [66], a composite for a given year was produced in the form of a median mosaic of all available Landsat scenes. To address the shortage of cloud-free images, we included the Landsat scenes of the year before and the year after the target year in the composite. By referring to previous research, six bands were retrieved, i.e., Band 1 (blue), Band 2 (green), Band 3 (red), Band 4 (near-infrared), Band 5 (shortwave infrared 1), and Band 7 (shortwave infrared 2), all with a spatial resolution of 30 m [65]. Figure 4 presents the cloud-free Landsat composites with standard false-color band combination from 1985 to 2010. Due to the shortage of cloud-less images, there are missing data in western areas of China in some target years. As these areas are usually sparsely populated with slight variation, we used the valid data in the nearest adjacent year to supplement these areas.

Previous studies have revealed that the detailed characteristics of various landscapes can be well reflected by these 6 visible and invisible bands [54]. Figure 5 presents the probability density distribution of population count in the ground-truth samples and the example RS image patches that correspond to various population counts. Obviously, different magnitudes of population count correspond to distinct landscape characteristics in the RS image patches. The interplay between population count and RS images indicates the potential of estimating population count based only on RS images from Landsat-5 via a deep learning architecture.

2.2. Methods

2.2.1. Building a Mapping from RS Image Patches to Population Counts via ResNet-N Model

In this study, we view the gridded population estimation task as a regression problem. The method framework is shown in Figure 6. Given an image patch ${\theta }^i$ of the grid cell $i$ and the corresponding logarithmized population count $p_i$, we express our learning task as building a mapping function:

$$p_i=f\left({\theta }_i\right)$$

(1)

where $f\left(·\right)$ is the mapping function to be learned by deep learning models. Acknowledging the highly nonlinear and complex relationship between RS images and population count, a ResNet (specifically, ResNet-50 was adopted) model considering neighborhood effects (ResNet-N) was utilized to approximate such a complex mapping relationship [53]. The ResNet model is one of the state-of-the-art CNN architectures and has been widely adopted to mine geographical knowledge from RS images [55,56]. The fundamental building block of Resnet-50 is the bottleneck, a convolution layer with an identity shortcut connection, which solves the problem of gradient vanishing [55]. As shown in Figure 6, ResNet-50 contains 7 layers (groups). Conv1 is a plain convolution layer with 64 convolution kernels of size 3 × 3, which slide on the RS image to extract hidden features and output 64 feature maps. Conv2 contains 3 bottleneck blocks, each with 128 convolution kernels of size 3 × 3, which slide on the feature maps generated by Conv1 to extract higher-level features. Likewise, Conv3 contains 4 bottleneck blocks, each with 512 convolution kernels; Conv4 contains 6 bottleneck blocks, each with 1024 convolution kernels, and Conv5 contains 3 bottleneck blocks, each with 2048 convolution kernels. In the network, deeper layers excavate more abstract and informative features related to the task from previous feature maps. Between each convolution layer (or bottleneck block), the feature map is reduced by half to aggregate information. Finally, the average pooling layer squeezes the feature map to 1 dimension, which is inputted into the fully connected layer (fc) to regress the population count. The ReLU activation function and batch normalization are used in all convolution layers to facilitate the training of networks [67]. Figure A1 illustrates how the input RS image evolves to the output population count in the network. Because of the autocorrelation of population distribution, the center grid cell population count may be affected by landscapes in the neighborhood. Hence, we constructed extended image patches by extending the center image patch to include its 3 × 3 neighboring patches to embed neighborhood knowledge [53,68]. Hence, the layer-wise convolutional operations of the ResNet model can extract interior and neighborhood and integrate latent features for population estimation when sliding on the extended image patches. In order to regress the population count directly, the softmax activation function in the final fully connected layer was removed. We used the log-cosh function for back-propagation training:

$$Loss\left(\widehat{p},p\right)={{\displaystyle \sum }}_{i=1}^{s}lo{g}_{10}\left(\cos \mathrm{h}\left(\widehat{p_i}-p_i\right)\right)$$

(2)

where $Loss\left(\widehat{p},p\right)$ is the log-cosh loss function, $p_i$ is the ground-truth population count of grid cell $i$, $\widehat{p_i}$ is the estimated population count of grid cell $i$, and $\cos \mathrm{h}\left(·\right)$ is the hyperbolic cosine function [68]. The log-cosh loss is similar to the L1 loss, commonly used in regression problems, but is more tolerant of anomalous estimations and achieves better performance [68]. Hyperparameters were tuned empirically based on 1/10 of the available samples. A stochastic gradient descent (SGD) optimizer with a momentum of 0.9 and a learning rate of ${10}^{-4}$ was used for weight updating. The batch size and the maximum number of epochs were set to 32 and 1000, respectively. The framework was implemented using the Tensorflow 2.0 library on a Linux server with a 2.50 GHz Intel Xeon E5-2680 CPU, an NVIDIA GTX 2080Ti GPU, and 128GB RAM.

2.2.2. Mapping Multi-Temporal Population Distributions in China via ResNet-N Model and Landsat-5 RS Images

This study aims to produce multi-temporal gridded population maps with 1 km spatial resolution for China via establishing a framework integrating a deep learning model with Landsat-5 RS images from GEE. Our research area, mainland China, is covered by a grid of 7346 × 4507 consisting of 1 km × 1 km cells. We excluded grid cells with a population count of <10 in the ground-truth population grid in 2010, which can be regarded as uninhabited areas, to reduce the computational burden, resulting in 5,508,904 grid cells being retained. A 1 km × 1 km cell in the population grid approximately covers a 34 × 34 image patch with a spatial resolution of 30 m on Landsat-5 composites. To consider the contribution of neighborhood effects on population count, we constructed extended image patches with a width and height of 102, including the center patch and its 3 × 3 neighboring patches. The extended image patch was then resized to a fixed size of 129 × 129 for inputting into the deep learning model. We obtained a centroid for each cell in the population grid and extracted a 102 × 102 image patch center around the obtained centroid from the Landsat-5 composites for each target year from 1985 to 2010. A total of 33,053,424 RS image patches were extracted and normalized to 0–1. Among them, the image patches that corresponded to the 2010 ground-truth population samples were utilized for training, evaluating, and testing the deep learning model. Once the model was trained, all RS image patches were inputted into the model to measure the population count of each position of each target year.

2.2.3. Modifying Raw Population Estimation via Census Data

Ensuring that the aggregated grid population counts at census units match the known official total population count is necessary. The dasymetric mapping method is used to achieve this goal. For a census unit $s$ with a known official total population count $p_s$, the following equations are used to modify the raw population estimations:

$$w_i=\frac{p_i^r}{{{\displaystyle \sum }}_{i\in S}{p}_i^r}$$

(3)

$$p_i^m=p_S\times w_i$$

(4)

where $p_i^r$ is the raw population count of cell $i$ estimated by the deep learning model, $w_i$ is the distribution weight of cell $i$, and $p_i^m$ represents the modified population count of cell $i$. In 2010, we used county-scale census data from the National Bureau of Statistics of China to modify the estimation. Due to data limitations, we used the city-scale (level 2 administrative unit) total population count from WorldPop generated using the dasymetric method based on county-scale census data to modify estimations for 2005 and 2000 [48]. For 1995 and 1990, we used the city-scale total population count from GPWv3 produced by the areal weighting method based on official census data at the county scale to modify the estimations [45]. For 1985, due to the unavailability of census data, a single country-wide population count from the World Bank Database was used for modification. The data source and administrative unit level of the census data or total population count are summarized in

Table A1. Source and administrative unit level of census data or total population count for modifying raw population estimation of each year.

Year	Administrative Unit Level	Source
1985	Country	World Bank Database
1990	City	GPWv3
1995	City	GPWv3
2000	City	WorldPop
2005	City	WorldPop
2010	County	National Bureau of Statistics of China

.

2.2.4. Accuracy Assessment

We used six quantitative metrics to assess the performance of the proposed population mapping framework and the produced multi-temporal gridded population data, including Pearson’s correlation coefficient (R), the coefficient of determination (R²), mean absolute error (MAE), percentage mean absolute error (%MAE), root mean squared error (RMSE), and percentage root mean squared error (%RMSE):

$$R={{\displaystyle \sum }}_{i=1}^n\frac{\left(p_{i,o}-\overline{p_o}\right)\left(p_{i,s}-\overline{p_s}\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(p_{i,o}-\overline{p_o}\right)}^2}\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(p_{i,s}-\overline{p_s}\right)}^2}}$$

(5)

$$R^2=\frac{n{{\displaystyle \sum }}_{i=1}^n{p}_{i,o}{p}_{i,s}-{{\displaystyle \sum }}_{i=1}^n{p}_{i,o}{{\displaystyle \sum }}_{i=1}^n{p}_{i,s}}{\sqrt{n{{\displaystyle \sum }}_{i=1}^n{p}_{i,o}{}^2-{\left({{\displaystyle \sum }}_{i=1}^n{p}_{i,o}\right)}^2}\sqrt{n{{\displaystyle \sum }}_{i=1}^n{p}_{i,s}{}^2-{\left({{\displaystyle \sum }}_{i=1}^n{p}_{i,s}\right)}^2}}$$

(6)

$$MAE=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n\left|p_{i,o}-p_{i,s}\right|$$

(7)

$$\%MAE=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n\frac{\left|p_{i,o}-p_{i,s}\right|}{p_{i,o}}$$

(8)

$$RMSE=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{\left(p_{i,o}-p_{i,s}\right)}^2}$$

(9)

$$\%RMSE=\frac{\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{\left(p_{i,o}-p_{i,s}\right)}^2}}{\overline{p_o}}$$

(10)

where $p_{i,o}$ is the ground-truth population count of the $i^{th}$ sample, $p_{i,s}$ denotes the estimated population count of the $i^{th}$ sample, n represents the total number of samples, $\overline{p_o}$ is the average of the ground-truth population count, and $\overline{p_s}$ is the average of the estimated population count. The indicator R, ranging from −1 to 1, measures the linear correlation between actual values and estimated values to evaluate the relative magnitude fitting performance [62]. The indicator R², with a value from -infinity to 1, measures how much variance in actual values is captured by the predicted values, assessing the absolute magnitude fitting performance [53]. R and R² evaluate the explainability of estimated values to actual values. MAE designates the average absolute error between actual values and estimated values. In order to highlight large errors, absolute errors are squared in RMSE. Since MAE and RMSE are not as understandable, the percentage errors (%MAE and %RMSE) assessing the proportion of the error to the actual value are also presented [54]. These 4 error metrics evaluate the absolute and percentage estimation error together. The mentioned 6 metrics complement each other and provide a comprehensive assessment of the proposed framework and the produced data [69].

3. Results

3.1. Accuracy Assessment of ResNet-N Model for Population Estimation

In this study, a ResNet-N model with neighbor augmentation was utilized to establish the end-to-end mapping between Landsat-5 RS image patches and population count. The model’s performance of directly estimating the population count from RS images was evaluated by the collected 20,000 testing samples. Figure 7 shows the scatterplots of ground-truth population count (p) and estimated population count ($\widehat{p}$) with their probability density distributions. As shown in Figure 7, the scatterplots of $p$ and $\widehat{p}$ present a clustered distribution pattern along the 1:1 reference line, validating that the deep learning architectures can effectively establish the mapping from RS image patches to population count. The probability density distributions of p and $\widehat{p}$ exhibit similar shapes and also confirm this conclusion. Compared to the ResNet model without neighbor augmentation, the ResNet-N model with neighbor augmentation used in this study displays superior performance in terms of the six evaluation metrics. ResNet-N (R = 0.84, R² = 0.70) exhibits higher explainability of landscape characteristics extracted from the RS images on population count compared to ResNet (R = 0.70, R² = 0.56). The R² indicates that 70% of the variance population count can be explained by the ResNet-N, compared to 56% by the ResNet. ResNet-N (%MAE = 13.63%, %RMSE = 15.91%) also has higher absolute accuracy than ResNet (%MAE = 16.06%,%RMSE = 19.35%). The %RMSE of ResNet -N is lower than that of ResNet by 21.62% and %MAE by 17.93%. The comparatively low %RMSE and %MSE of both models reveal the capacity of the deep learning model to capture the heterogeneity in population distribution from RS images, and improved estimation performance can be achieved considering neighbor effects.

For true population count ($p$) and estimated population count ($\widehat{p})$, an investigation of the relationship between $p$ and $\widehat{p}-p$ was conducted to explore the systematic bias of estimating population count from RS images via deep learning technologies. Figure 8 shows the scatterplots of $p$ and $\widehat{p}-p$ from ResNet-N and ResNet. The results reveal that both models tend to underestimate densely populated samples and overestimate sparsely populated samples, evidenced by the significant negative correlation coefficient and the negative slope. The observed bias can be ascribed to the inherent limitations of multispectral RS images, which cannot identify the social–economic factors that affect population distribution (i.e., the high utilization efficiency of space in densely populated areas). However, consideration of neighbor effects leads to reduced biases and better estimation performance [53].

Interpretability is a critical aspect of a model [53,59]. A model with good interpretability usually has good performance. In this study, the ResNet-N model considers only RS images as input to estimate population count. Therefore, all estimations can be explained in terms of the landscape details from RS images. We used gradient-weighted class activation mapping (Grad-CAM), a visual explanation technology for deep learning models, to figure out what features our model learns to estimate population count [70]. Grad-CAM can output a heatmap for an RS image patch. The heat value quantifies the relative contribution of input pixels in the original patch to the estimated population count [70]. For analysis, we selected 12 typical grid cells with different magnitudes of population count. Figure 9 presents the RS image patches in the top rows and corresponding heatmaps in the bottom rows. As shown in Figure 9a, built-up areas are highlighted in heatmaps when they border natural areas. The explanation for this is that built-up areas are usually more densely populated than natural areas. Figure 9b proves the ability of our model to recognize different buildings by capturing hidden hierarchic features of RS images in the interior of the built-up area to estimate population count. As densely populated buildings (i.e., residential) and sparsely populated buildings (i.e., factories) are staggered in the built-up area, distinguish different buildings contributes to accurate population estimation. The heatmaps offer insights into how human activities interact with the underpinning physical environment and prove that our model can learn valuable features for population estimation.

3.2. Validating Multi-Temporal Gridded Population Data via Census Data

A stable end-to-end mapping from RS image patches to population count was established by the ResNet-N model. It is promising that population distribution mapping can be achieved with only the formed mapping and RS images. However, it is necessary to ensure that the aggregated grid population counts at census units match the known official total population count. Furthermore, the grid cell estimation will be more accurate when scaled to match the true population value [59]. We used county-level census data to modify the raw population count estimated from RS images by the model in 2010. Validation of the modified population map was conducted using town-level census data. It is a common practice in dasymetric mapping to use census data of a finer scale to evaluate the accuracy of the produced gridded population data [39]. Two well-known gridded population datasets, WorldPop [48] and GPWv4 [45], were selected as baselines to highlight the performance of the produced data. We collected towns with a population of >100 to assess the comparative performance of the produced gridded data. As shown in

Table 1. Accuracy assessment of RSPop at town scale comparing WorldPop and GPWv4.

	RSPop	WorldPop	GPWv4
R	0.89	0.87	0.82
R2	0.77	0.69	0.61
MAE	7846.62	8138.20	9463.33
%MAE	46.21	51.19	62.48
RMSE	15,686.74	18,277.52	20,448.11
%RMSE	56.03	65.28	73.03

, our new population map produced by coupling RS images and deep learning technologies (referred to as RSPop) achieved the best performance, with the lowest absolute and relative errors and the highest explainability and correlation with the true population count. Figure 10 presents scatterplots of the true population count and estimated population count of each town from RSPop, WorldPop, and GPWv4. Compared to other gridded population data, the scatterplot of RSPop presents a more concentrated distribution pattern along the 1:1 reference line, with the highest accuracy. In contrast, points are scattered and distributed away from the 1:1 reference line in GPWv4, which has the lowest accuracy.

The gridded population data in 2010 produced by the proposed framework were validated and achieved the highest performance compared to other datasets. Due to the consistency of Landsat-5 images and the relative stability of human activity patterns, it can be expected that accurate gridded population data from 1985 to 2005 can be produced by the same framework, using corresponding RS images at target years as input. For the period of 1990–2005, because town-scale census data are challenging to collect, we used the city-scale total population count to modify the estimated population count and applied the county-scale total population count to verify the accuracy of the data. Total population counts at city scale and county scale in 2000 and 2005 were obtained from WorldPop, while total population counts at city scale and county scale for 1990 and 1995 were obtained from GPWv3. Both WorldPop and GPWv3 were produced based on county-scale census data [45,48]. Therefore, it would be impractical to use them for comparative analysis. Instead, as the accuracy of the gridded population data in 2010 has been verified, the population estimation in 2010 modified by city-scale census data was used for comparison at the county scale. As shown in

Table 2. Accuracy assessment of RSPop at county scale from 1990 to 2010.

	1990	1995	2000	2005	2010
R	0.86	0.86	0.94	0.95	0.97
R2	0.74	0.73	0.88	0.91	0.93
MAE	93,260.92	103,362.10	83,413.22	77,668.16	69,052.32
%MAE	30.68	28.48	22.11	19.67	16.64
RMSE	163,431.57	182,624.46	127,106.24	116,733.57	105,319.00
%RMSE	38.45	40.74	27.43	24.47	21.49

, overall performance reductions exist for each target year in 1990–2005 compared to 2010. For example, the R² is reduced from 0.93 in 2010 to 0.91 in 2005, 0.88 in 2000, 0.73 in 1995, and 0.74 in 1990, with an average reduction of 12.37%. Figure 11 shows scatterplots of the true population count and estimated population count at the county level, which present clustered patterns along the 1:1 reference line. These results imply that the model trained in 2010 is generalizable to other years.

For 1985, as the corresponding census data were unavailable, we used a single country-wide population count from the World Bank Database to modify gridded population data and have not verified it. Due to the consistency of the proposed population mapping framework, we argue that data accuracy in 1985 is comparable to that in other years.

3.3. Accuracy Analysis of Gridded Population Data to Scales of Census Data

The availability of census data restrains the production of gridded population data, and fine-scale census data benefit accurate population mapping [48]. However, census surveys are time-consuming and labor-intensive, and, in many cases, only coarse-grained census data can be obtained [71]. Here, we utilized the population distribution in 2010 to investigate the difference in the accuracy of gridded population data based on census data of different scales. The true population and the estimated population at the town scale were compared to evaluate the accuracy of the modified data. Figure 12 shows scatterplots of the true population count and estimated population count at the town scale from gridded population data based on county-scale, city-scale, province-scale, and country-scale census data. The points of true and estimated values present clustered distribution along the 1:1 reference line at all scales, suggesting that the produced gridded population data based on all census scales can capture the heterogeneity in population distribution. Figure 13 shows the variation in the accuracy of gridded population distribution based on census data of four different scales in terms of six accuracy metrics. It is shown that with the increase in the scale of census units, data accuracy decreases. Therefore, when census data are available, it is necessary to use them to modify the raw estimations and obtain better accuracy. Comparable to GPWv4 (R² = 0.61, %RMSE = 73.03), based on county-census data, the R² and %RMSE of gridded population data based on a single country-wide population count is 0.55 and 79.14, with a difference of 9.84% and 8.37%, respectively. As the difference is relatively low and a single country-wide population count is easily accessible, it is promising that the constructed framework can generate reliable gridded population data from RS images without census data efficiently.

3.4. Evolution of China’s Population Distribution from 1985 to 2010

Figure 14 shows the produced gridded population maps of China with the resolution of 1 km for the years 1985, 1990, 1995, 2000, 2005, and 2010. Although the total population of China grew from 105,104,000 in 1985 to 133,770,500 in 2010, the pattern of population distribution has not changed significantly. The famous Hu-Line pattern [72], characterized by a dense population in the southeast part and a sparse population in the northwest areas of China, remains. From 1985 to 2010, the population gravity center [73] of China lay roughly at the point (113.89° E, 32.97° N), which showed a slight movement to the southeast, with a moving distance of fewer than 33 km (Figure A2), suggesting that China’s population and economic center was moving towards the southeast area. In line with previous studies, China’s population density is classified into eight levels in this study [34]. Among them, grid cells with a population density greater than 1500 persons/km² are regarded as high-density regions, cells with a population density between 200 and 1500 are regarded as medium-density regions, and cells with a population density less than 200 are regarded as low-density regions.

Table 3. Percentage values of area and population for different density levels.

Density	1985		1990		1995		2000		2005		2010
	Area	Population	Area	Population	Area	Population	Area	Population	Area	Population	Area	Population
Low	83.19	22.49	82.33	20.48	82.76	19.46	83.79	18.26	83.97	17.62	83.91	16.44
Medium	16.40	61.18	17.2	60.54	16.64	56.21	15.42	50.96	15.12	48.22	15.07	47.66
High	0.42	16.33	0.48	18.98	0.61	24.33	0.79	30.78	0.92	34.17	1.02	35.90

lists the percentage values of the area and population for different levels, reflecting the evolution of China’s population distribution from 1985 to 2010.

From 1985 to 2010, the area proportion of high-density regions increased from 0.42% to 1.02%, increasing by 145%, and the population proportion increased from 16.33% to 35.90%, increasing by 119.84%. Previous researches have suggested that high-density regions with a population density of >1500 persons/km² can be regarded as urbanized regions [34]. The expansion of regions with high population density can be ascribed to rapid urbanization and the emergence of megacities due to China’s reform and opening-up policy. The area proportion of medium-density regions decreased from 16.40% in 1985 to 15.07% in 2010, a decrease of 4.46%, and the population proportion decreased from 61.18% to 47.66%, decreasing by 22.09%. The expansion of megacities can explain the reduction in regions with medium population density as the concentration of the population in megacities leads to the contraction of small- and medium-sized urban regions. The area proportion of low-density regions increased from 83.19% in 1985 to 83.91% in 2010, while the population proportion decreased from 22.49% to 16.44%. The expansion of low-density regions may be attributed to immigration measures in some mountainous areas to protect the ecological environment and alleviate poverty [24]. However, with urbanization, the population becomes gradually concentrated in urban regions, leading to a reduced population in low-density regions.

Figure 15 shows the population distributions and landscape variations of three regions in large urban agglomerations in China from 1985 to 2010: (a) Beijing-Tianjin-Hebei, (b) the Yangtze River Delta, and (c) the Pearl River Delta. During this period, these areas experienced rapid urban expansion and consequent population growth, which further led to the transformation of the urban landscape. The produced continuous multi-temporal gridded population data with high spatial resolution provide support to track the co-evolvement of the human population and physical landscape.

4. Conclusions and Discussion

China, as the most populous developing country in the world, has experienced rapid economic development, population growth, and urbanization in recent decades. Fine-scale population distribution data and their dynamics are a crucial component in many fields, including resource management, disaster response, public health, urban planning, and climate change; they are also fundamental in monitoring and achieving sustainable development goals (e.g., SDG 11.6.2—annual mean levels of fine particulate matter (e.g., PM2.5 and PM10) in cities (population-weighted)) [74]. However, due to the lack of adequate methodology and appropriate data, there are rarely continuous multi-temporal gridded population data available for China over a long historical period to aid in our understanding of the evolution of population distribution.

The continuously improving remote sensing technology provides low-cost, broad-coverage, and high spatiotemporal resolution ground information, which, in conjunction with deep learning technology that can mine hidden geographical knowledge, enables continuous population distribution mapping. We introduced a framework integrating a ResNet-N deep learning architecture with the consideration of neighborhood effects with a vast number of Landsat-5 images from GEE for rapid multi-temporal population mapping over a long historical period in this study. The ResNet-N model was developed to establish the end-to-end mapping between population count and RS image patches. Based on the trained model, we estimated the gridded population count (1 km × 1 km) of China with corresponding Landsat-5 image patches from GEE as input from 1985 to 2010. The produced raw estimations were adjusted by available census data to acquire the final gridded population data.

The ResNet-N model with neighbor augmentation achieved R² 0.70 and %RMSE 15.91%, with a better explainability and higher absolute accuracy than ResNet, which can model the interaction between the physical environment and population and capture the heterogeneity in population distribution from RS images. An interpretation analysis revealed that the constructed deep learning model could provide valuable features for population estimation since it can distinguish the differences between natural and built-up areas and between densely populated and sparsely populated buildings. The produced gridded population data in 2010 was validated via town-scale census data and showed higher accuracy than WorldPop and GPWv4. The produced gridded population data from 1990 to 2005 were validated via county-scale total population count and achieved comparable performance to data in 2010, suggesting that the produced gridded population map can analyze spatiotemporal characteristics of China’s population distribution over a long period with acceptable accuracy.

The spatiotemporal analysis of multi-temporal gridded population data showed that China’s population distribution pattern did not change significantly from 1985 to 2010, and the famous Hu-Line pattern remains. With China’s urbanization process and the emergence of megalopolises, the high-density population regions have dramatically expanded, with the area expanding by approximately 145% and the population expanding by approximately 120%. The concentration of the population in big cities has led to the contraction of cities with medium and small sizes. China’s medium-density regions have shrunk by around 4.46%, and their population has decreased by approximately 22.09%. China’s low-density regions have expanded slightly with China’s poverty alleviation and mountain migration strategy [24], but the population has decreased.

The coupling of deep learning technologies and easily accessible, regularly updated, and analysis-ready remote sensing data from GEE unquestionably establishes a novel avenue that promotes multi-temporal population mapping over a long period at a large scale. However, there are several limitations of this framework. First, although informative knowledge of the population distribution can be extracted from RS images directly, socioeconomic information cannot be identified. For example, the vacancy rate of buildings is difficult to capture, making it impossible to distinguish between vacant buildings and occupied buildings [54]. Especially in China, unreasonable urban expansion has led to the appearance of ghost cities characterized by high vacancy rates of buildings, which cause overestimation of the population [75,76]. Social sensing data and nighttime light data can depict multiple facets of human society, capturing related socioeconomic information [69,75]. In the future, integrating multi-source RS data and time-series social sensing data can further improve the framework [23]. Second, we produced the gridded population data for each target year independently. However, as population distribution is continuous in the time dimension, specific time-series analysis techniques are needed to stabilize temporal variation in population distribution [17]. Third, the deep learning model ResNet-N was trained based on samples collected from the entirety of China in 2010. Although the generalization performance to other years of the model trained in 2010 has been validated, further efforts are needed in considering generalization errors. As China has a large territory and exhibits significant internal variations, in the future, we will investigate whether using regionally parameterized models will improve the performance of population mapping [59].

The framework proposed in this paper demonstrates the feasibility of mapping multi-temporal gridded population distribution at a large scale over a long period in a timely and low-cost manner, which is particularly useful in low-income and data-poor regions. The framework can also be easily extended to a global scale or to map other gridded socioeconomic variables (e.g., GDP) for monitoring and assessing progress toward fulfillment of the SDGs [12].