Assessing the Reliability of Satellite and Reanalysis Estimates of Rainfall in Equatorial Africa
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Sets
2.1.1. Overview
2.1.2. Satellite Rainfall Products
2.1.3. Gauge Data Sets
2.1.4. Reanalysis Data Sets
2.1.5. Other Data Sets
2.2. Methodology
3. Results
3.1. Mean Rainfall
3.1.1. Central Equatorial Africa
3.1.2. Lake Victoria and Its Catchment
3.2. The Seasonal Cycle
3.2.1. Congo Basin
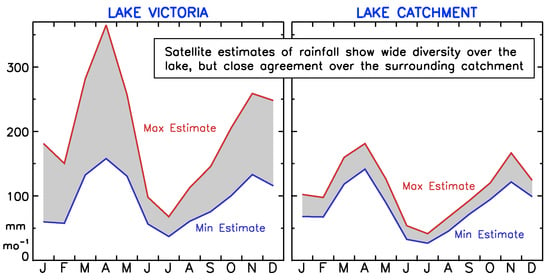
3.2.2. Lake Victoria and Its Catchment
3.3. Interannual Variability and Trends
3.3.1. Congo Basin
3.3.2. Lake Victoria
3.3.3. Trends
3.4. Links to Large-Scale Factors in Variability
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A review of global precipitation data sets: Data sources, estimation, and inter-comparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Nicholson, S.E.; Klotter, D.; Zhou, L.; Hua, W. Validation of satellite precipitation estimates over the Congo Basin. J. Hydrometeor. 2019, 20, 631–656. [Google Scholar] [CrossRef] [Green Version]
- Washington, R.; James, R.; Pearce, H.; Pokam, W.M.; Moufouma-Okia, W. Congo Basin rainfall climatology: Can we believe the climate models? Philos. Trans. Roy. Soc. B 2013, 368, 20120296. [Google Scholar] [CrossRef]
- Hua, W.; Zhou, L.; Nicholson, S.E.; Chen, H.; Qin, M. Assessing reanalysis data for understanding rainfall climatology and variability over central Equatorial Africa. Clim. Dyn. 2019, 53, 651–669. [Google Scholar] [CrossRef] [Green Version]
- Nicholson, S.E.; Klotter, D.; Hartman, A.T. Lake-effect rains over Lake Victoria and their association with Mesoscale Convective Systems. J. Hydrometeor. 2021, 22, 1353–1368. [Google Scholar]
- Dinku, T.; Ceccato, P.; Ropelewski, C.F. Validation of satellite rainfall products over over East Africa’s complex topography. Int. J. Remote Sens. 2007, 29, 1503–1526. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzamwa, S.; Ropelewski, C.F. Validation of high-resolution satellite rainfall products over complex terrain. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- Dinku, T.; Connor, S.J.; Ceccato, P. Comparison of CMORPH and TRMM-3B42 over mountainous regions of Africa and South America. In Satellite Rainfall Applications for Surface Hydrology; Springer: Dordrecht, The Netherlands, 2010; pp. 193–204. [Google Scholar]
- Dinku, T.; Ceccato, P.; Connor, S.J. Challenges of satellite rainfall estimation over mountainous and arid parts of east Africa. Int. J. Remote Sens. 2011, 21, 5965–5979. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Evaluation through independent measurements: Complex terrain and humid tropical region in Ethiopia. In Satellite Rainfall Applications for Surface Hydrology; Springer: Dordrecht, The Netherlands, 2010; pp. 205–214. [Google Scholar]
- Bartsotas, N.S.; Aganostou, E.N.; Nikolopoulos, E.I.; Kallos, G. Investigating satellite precipitation uncertainty over Complex Terrain. J. Geophys. Res.–Atmos. 2018, 123, 5346–5359. [Google Scholar] [CrossRef]
- Ehsan Bhuiyan, M.A.; Nikolopoulos, E.I.; Anagnostou, E.N. Machine Learning-Based Blending of Satellite and Reanalysis Precipitation Datasets: A Multiregional Tropical Complex Terrain Evaluation. J. Hydrometeor. 2019, 20, 2147–2161. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Elshamy, M.; van Griensven, A.; Soliman, E.; Kigobe, M.; Ndomba, P.; Mutemi, J.; Mutua, F.; Moges, S.; Xuan, Y.; et al. Future hydrology and climate in the River Nile basin: A review. Hydrolog. Sci. J. 2011, 56, 199–211. [Google Scholar] [CrossRef] [Green Version]
- Sene, K.J. Theoretical estimates for the influence of Lake Victoria on flows in the upper White Nile. Hydrolog. Sci. J. 2000, 45, 125–145. [Google Scholar] [CrossRef] [Green Version]
- Akurut, M.; Willems, P.; Niwagaba, C.B. Potential Impacts of Climate Change on Precipitation over Lake Victoria, East Africa, in the 21st Century. Water 2014, 6, 2634–2659. [Google Scholar] [CrossRef] [Green Version]
- Vanderkelen, I.; van Lipzig, N.P.M.; Thiery, W. Modelling the water balance of Lake Victoria (East Africa)-Part 2: Future projections. Hydrol. Earth Syst. Sci. 2018, 22. [Google Scholar] [CrossRef] [Green Version]
- Kent, C.; Chadwick, R.; Rowell, D.P. Understanding uncertainties in future projections of seasonal tropical precipitation. J. Clim. 2015, 28, 4390–4413. [Google Scholar] [CrossRef]
- Otieno, V.O.; Anyah, R.O. CMIP5 simulated climate conditions of the Greater Horn of Africa (GHA). Part II: Projected climate. Clim. Dyn. 2013, 41, 2099–2113. [Google Scholar] [CrossRef]
- Souverijns, N.; Thiery, W.; Demuzere, M.; Van Lipzig, N.P.M. Drivers of future changes in East African precipitation. Environ. Res. Lett. 2016, 11, 114011. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Tian, Y.; Myneni, R.B.; Ciais, P.; Saatchi, S.; Liu, Y.Y.; Piao, S.; Chen, H.; Vermote, E.F.; Song, C.; et al. Widespread decline of Congo rainforest greenness in the last decade. Nature 2014, 509, 86–90. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, S.E. The rainfall and convective regime over equatorial Africa, with emphasis on the Congo Basin. In Congo Basin Hydrology, Climate and Biogeochemistry: A Foundation for the Future; Alsdorf, D., Ed.; AGU Geophysical Monograph: Washington, DC, USA, 2021; in press. [Google Scholar]
- Nicholson, S.E.; Fink, A.H.; Funk, C. Meteorological causes of the catastrophic floods of October/November 2019 in equatorial Africa. Glob. Planet. Chang. 2021, in press. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T. TRMM and Other Data Precipitation Data Set Documentation. NASA TRMM Doc. 2014, 42. Available online: https://gpm.nasa.gov/sites/default/files/document_files/3B42_3B43_doc_V7.pdf (accessed on 1 February 2021).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multi-satellite precipitation analysis: Quasi-global, multi-year, combined-sensor precipitation estimates at finer scale. J. Hydrometeor. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, J.G.; Bolvin, D.T.; Nelkin, E.J. Day 1 IMERG Final Run Release Notes. NASA Doc. 2015, 9. Available online: http://pmm.nasa.gov/sites/default/files/document_files/IMERG_FinalRun_Day1_release_notes.pdf (accessed on 1 March 2021).
- Cattani, E.; Merino, A.; Levizzani, V. Evaluation of monthly satellite-derived precipitation products over East Africa. J. Hydrometeor. 2016, 17, 2555–2573. [Google Scholar] [CrossRef]
- Dezfuli, A.K.; Ichoku, C.M.; Huffman, G.J.; Mohr, K.; Selker, J.S.; Van De Giesen, N.; Hochreutener, R.; Annor, F.O. Validation of IMERG precipitation in Africa. J. Hydrometeor. 2017, 18, 2817–2825. [Google Scholar] [CrossRef] [PubMed]
- Beighley, R.E.; Ray, R.; He, Y.; Lee, H.; Schaller, L.; Andreadis, K.M.; Durand, M.; Alsdorf, D.E.; Shum, C.K. Comparing satellite derived precipitation datasets using the Hillslope River Routing (HRR) model in the Congo River Basin. Hydrolog. Process. 2011, 25, 3216–3229. [Google Scholar] [CrossRef]
- Awange, J.L.; Ferreira, V.G.; Forootan, E.; Andam-Akorful, S.A.; Agutu, N.O.; He, X.F. Uncertainties in remotely sensed precipitation data over Africa. Int. J. Climatol. 2016, 36, 303–323. [Google Scholar] [CrossRef] [Green Version]
- Diem, J.E.; Hartler, J.; Ryan, S.J. Validation of satellite rainfall products for western Uganda. J. Hydrometeor. 2014, 15, 2030–2036. [Google Scholar] [CrossRef]
- Asadullah, A.; McIntyre, N.; Kigobe, M. Evaluation of five satellite products for estimation of rainfall over Uganda. Hydrolog. Sci. J. 2008, 53, 1137–1150. [Google Scholar] [CrossRef]
- Guo, R.F.; Lui, Y.B. Evaluation of satellite precipitation products with rain gauge data at different scales: Implications for hydrological applications. Water 2016, 8, 281. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. Integrated Multi-Satellite Retrievals for GPM (IMERG) Technical Documentation (Technical Documentation). NASA 2019, 71. Available online: https://pmm.nasa.gov/data-access/downloads/gpm (accessed on 1 March 2021).
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [Green Version]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Amer. Meteor. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The Version 2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979-Present). J. Hydrometeor. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Xie, P.; Arkin, P.A. Analyses of global monthly precipitation using gauge observations, satellite estimates, and numerical model predictions. J. Clim. 1996, 9, 840–858. [Google Scholar] [CrossRef] [Green Version]
- Xie, P.; Arkin, P.A. Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull. Amer. Meteor. Soc. 1997, 78, 2537–2558. [Google Scholar] [CrossRef]
- Love, T.B.; Kumar, V.; Xie, P.; Thiaw, W. A 20-Year Daily Africa Precipitation Climatology Using Satellite and Gauge Data. Preprints. In Proceedings of the 14th Conference on Applied Meteorology, Seattle, WA, USA, 2004; Available online: http://ams.confex.com/ams/pdfpapers/67484.pdf (accessed on 1 March 2021).
- Novella, N.S.; Thiaw, W.M. African Rainfall Climatology Version 2 for famine early warning systems. J. Appl. Meteor. Climatol. 2013, 52, 588–606. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeor. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Xie, P.; Joyce, R.J.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. Reprocessed, bias-corrected CMORPH CRT global high resolution estimates form 1998. J. Hydrometeor. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
- Xie, P.; Janowiak, J.E.; Arkin, P.A.; Adler, R.; Gruber, A.; Ferraro, R. GPCP pentad precipitation analyses: An experimental data set based on gauge observations and satellite estimates. J. Clim. 2003, 16, 2197–2214. [Google Scholar] [CrossRef] [Green Version]
- Maidment, R.I.; Grimes, D.I.F.; Allan, R.; Greatrex, H.; Rojas, O.; Leo, O. Evaluation of satellite-based and model re-analysis rainfall estimates for Uganda. Meteorol. Appl. 2013, 20, 308–317. [Google Scholar] [CrossRef] [Green Version]
- Maidment, R.; Grimes, D.; Allan, R.P.; Tarnavsky, E.; Stringer, M.; Hewison, T.; Roebeling, R.; Black, E. The 30 year TAMSAT African Rainfall Climatology And Time series (TARCAT) data set. J. Geophys. Res. 2014, 119, 10,619–10,644. [Google Scholar] [CrossRef] [Green Version]
- Tarnavsky, E.; Grimes, D.; Maidment, R.; Black, E.; Allan, R.P.; Stringer, M. Extension of the TAMSAT satellite-based rainfall monitoring over Africa and fro 1983 to present. J. Appl. Meteor. Climatol. 2014, 53, 2805–2822. [Google Scholar] [CrossRef] [Green Version]
- Maidment, R.I.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.; Nkonde, E.; Senkunda, S.; et al. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Sci. Data 2017, 4, 170063. [Google Scholar] [CrossRef]
- Nicholson, S.E. The spatial coherence of African rainfall anomalies: Interhemispheric teleconnections. J. Clim. Appl. Meteorol. 1986, 25, 1365–1381. [Google Scholar] [CrossRef] [Green Version]
- Nicholson, S.E.; Some, B.; Kone, B. An analysis of recent rainfall conditions in West Africa, including the rainy seasons of the 1997 el Niño and 1998 la Niña years. J. Clim. 2000, 13, 2628–2640. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Funk, C.; Fink, A.H. One and a half centuries of rainfall variability over the African continent. Glob. Planet. Chang. 2018, 165, 114–127. [Google Scholar] [CrossRef]
- Funk, C.C.; Nicholson, S.E.; Landsfeld, M.; Klotter, D.A.; Peterson, P.; Harrison, L. The Centennial Trends Greater Horn of Africa precipitation dataset. Sci. Data 2015, 2, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, S.E.; Klotter, D.; Dezfuli, A.K.; Zhou, L. New rainfall data sets for the Congo Basin and surrounding regions. J. Hydrometeor. 2018, 19, 1379–1396. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Ziese, M. GPCC Full Data Monthly Product Version 7 at 2.5: Monthly Land-Surface gauges built on GTS-based and Historic Data. GPCC Data Rep. 2015. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Hersbach, H.; Dee, D. ERA5 Reanalysis Is in Production ECMWF Newsletter; ECMWF: Reading, UK, 2016; Volume 147. [Google Scholar]
- Onogi, K.; Tsutsui, J.; Koide, H.; Sakamoto, M.; Kobayashi, S.; Hatsushika, H.; Matsumoto, T.; Yamazaki, N.; Kamahori, H.; Takahashi, K.; et al. The JRA-25 Reanalysis. J. Meteor. Soc. Jpn. 2007, 85, 369–432. [Google Scholar] [CrossRef] [Green Version]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Amer. Meteor. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.M. Extended Reconstructed Sea Surface Temperature version 5 (ERSSTv5), Upgrades, validations, and inter-comparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Saji, N.H.; Yamagata, T. Possible impacts of Indian Ocean Dipole mode events on global climate. Clim. Res. 2003, 25, 151–169. [Google Scholar] [CrossRef]
- Nicholson, S.E. Long-term variability of the East African ‘short rains’ and its links to large-scale factors. Int. J. Climatol. 2015, 35, 3979–3990. [Google Scholar] [CrossRef]
- Clark, C.O.; Webster, P.J.; Cole, J.E. Interdecadal variability of the relationship between the Indian Ocean zonal mode and East African coastal rainfall anomalies. J. Clim. 2003, 16, 548–554. [Google Scholar] [CrossRef] [Green Version]
- Ummenhofer, C.C.; Gupta, A.S.; England, M.H.; Reason, C.C.J. Contributions of Indian Ocean sea surface temperatures to enhanced East African rainfall. J. Clim. 2009, 22, 993–1013. [Google Scholar] [CrossRef] [Green Version]
- Bultot, F. Atlas climatique du bassin Congolais: Les composantes du bilan d’eau. Bruss. Inst. Natl. pour l’Étude Agron. du Congo. 1971, 2, 25. [Google Scholar]
- Jackson, B.; Nicholson, S.E.; Klotter, D. Mesoscale convective systems over western equatorial Africa and their relationship to large-scale circulation. Mon. Wea. Rev. 2009, 137, 1272–1294. [Google Scholar] [CrossRef]
- Nesbitt, S.W.; Cipelli, R.; Rutledge, S.A. Storm morphology and rainfall characteristics of TRMM precipitation features. Mon. Wea. Rev. 2006, 134, 2702–2721. [Google Scholar] [CrossRef] [Green Version]
- Flohn, H.; Burkhardt, T. Nile runoff at Aswan and Lake Victoria; An example of a discontinuous climate time series. Z. Gletscherk. Glazialgeol. 1985, 21, 125–130. [Google Scholar]
- Munzimi, Y.A.; Hansen, M.C.; Adusei, B.; Senay, G.B. Characterizing Congo Basin rainfall and climate using tropical rainfall measuring mission (TRMM) satellite data and limited rain gauge ground observations. J. Appl. Meteorol. Climatol. 2015, 54, 541–555. [Google Scholar] [CrossRef]
- Pombo, S.; de Oliveira, R.P.; Mendes, A. Comparative performance analysis of climate reanalysis approaches in Angola. Hydrolog. Sci. J. 2017, 62, 698–714. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Liu, T.; Huang, Y.; Ling, Y.; Li, Z.; Bao, A.; Chen, X.; Kurban, A.; De Maeyer, P. Satellite-based precipitation datasets evaluation using gauge observation and hydrological modeling in a typical arid land watershed of Central Asia. Remote Sens. 2021, 13, 221. [Google Scholar] [CrossRef]


















| Product | Start | End | Resolution | Global Coverage | |
|---|---|---|---|---|---|
| Spatial | Temporal | ||||
| ARC2 | 1/83 | present | 0.1° | daily | 40S–40N 20W–55E |
| CHIRPS 2.0 | 1981 | present | 0.05° | daily | 50S–50N 0–360 Long. |
| CMAP ENHANCED | 1/79 | present | 2.5° | pentad | Global |
| CMORPH CRT | 12/2002 | present | 8 km | sub-daily | 60S–60N 0–360 Long |
| GPCP V.3.1 | 1/83 | present | 0.5° | monthly | Global |
| IMERG-F | 6/2000 | present | 0.1° | sub-daily | Global |
| PERSIANN CDR | 1/83 | present | 0.25° | sub-daily | 60S–60N 0–360 Long |
| RFE 2.0 | 1/83 | present | 0.1° | daily | 40S–40N 20W–55E |
| TAMSAT V3 | 1/83 | present | 4 km | daily | 36S–38N 19W–52E |
| TRMM 3B43 V7 | 1/98 | 12/2019 | 0.25° | monthly | 50S–50N 180W–180E |
| Product | Start | End | Resolution | Global Coverage | |
|---|---|---|---|---|---|
| Spatial | Temporal | ||||
| CFSR | 1/1979 | 11/2017 | 0.25° | Sub-daily | Global |
| ERA5 | 1/1979 | Present | 0.10° | Sub-daily | Global |
| JRA55 | 1/1958 | Present | 0.56° | Sub-daily | Global |
| MERRA 2 | 1/1980 | Present | 0.5° × 0.625° | Sub-daily | Global |
| NCEP II | 1/1979 | Present | 2.0° × 2.0° | Sub-daily | Global |
| Source | Congo | Lake | Catchment | |||
|---|---|---|---|---|---|---|
| Ann | Nov | Ann | Nov | Ann | Nov | |
| IMERG | 1896 | 210 | 2372 | 259 | 1257 | 153 |
| TRMM | 1797 | 207 | 1714 | 206 | 1194 | 149 |
| GPCP V3.1 | 1887 | 204 | 1706 | 196 | 1175 | 137 |
| CHIRPS | 1815 | 178 | 1448 | 164 | 1172 | 134 |
| ARC2 | 1735 | 171 | 1522 | 180 | 1040 | 123 |
| RFE | 1713 | 179 | 1470 | 172 | 1051 | 122 |
| CMAP | 1854 | 196 | 1127 | 133 | 1245 | 167 |
| TAMSAT | 1954 | 188 | 1559 | 167 | 1179 | 131 |
| CMORPH | 1571 | 160 | 1800 | 208 | 996 | 126 |
| PERSIANN | 1830 | 205 | 1498 | 194 | 1169 | 146 |
| CFSR | 1405 | 158 | 1183 | 143 | 1353 | 145 |
| ERA5 | 1553 | 162 | 2093 | 253 | 1301 | 167 |
| JRA55 | 1685 | 198 | 535 | 86 | 706 | 101 |
| MERRA 2 | 1402 | 156 | 1933 | 292 | 1940 | 244 |
| NCEP II | 1758 | 202 | 886 | 151 | 1267 | 196 |
| GPCC | 1840 | 206 | 9999 | 9999 | 1200 | 144 |
| NIC131 | 1831 | 199 | 9999 | 9999 | 1218 | 129 |
| Source | Congo | Lake | Catchment | |||
|---|---|---|---|---|---|---|
| Ann | Nov | Ann | Nov | Ann | Nov | |
| IMERG | 0.44 | 0.12 | 0.17 | 0.04 | 0.22 | 0.09 |
| TRMM | 0.23 | 0.28 | 0.54 | 0.09 | −0.12 | −0.01 |
| GPCP V3.1 | 0.05 | 0.10 | 1.42 | 0.03 | 0.41 | 0.06 |
| CHIRPS | 0.08 | 0.12 | 1.08 | 0.16 | 0.89 | 0.16 |
| ARC2 | 0.88 | 0.06 | 1.43 | 0.30 | 0.71 | 0.24 |
| RFE | 1.95 | 0.21 | 3.62 | 0.47 | 1.07 | 0.20 |
| CMAP | −0.59 | 0.10 | 0.84 | 0.22 | 0.41 | 0.43 |
| TAMSAT | 0.37 | 0.16 | 0.62 | 0.10 | 0.81 | 0.21 |
| CMORPH | −0.80 | −0.09 | 3.14 | 0.30 | 0.35 | 0.17 |
| PERSIANN | 0.10 | 0.14 | 0.49 | 0.03 | −0.21 | 0.00 |
| CFSR | −0.48 | −0.32 | 2.72 | 0.34 | 3.66 | 0.42 |
| ERA5 | −1.06 | −0.08 | 0.88 | 0.02 | 0.72 | 0.05 |
| JRA55 | −1.15 | −0.19 | −0.47 | −0.02 | −1.05 | −0.01 |
| MERRA 2 | 2.01 | 0.28 | 4.44 | 0.63 | 6.04 | 0.88 |
| NCEP II | 4.19 | 0.74 | 1.16 | 0.12 | 0.94 | −0.33 |
| GPCC | 0.12 | 0.07 | N.A. | N.A. | 0.44 | 0.11 |
| NIC131 | −0.75 | −0.21 | N.A. | N.A. | −1.05 | 0.11 |
| PRODUCT | NIÑO | DMI | Equatorial Atlantic | Eastern Atlantic | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Lake | LC | C | Lake | LC | C | Lake | LC | C | Lake | LC | |
| IMERG | −0.49 | 0.39 | 0.54 | 0.65 | ||||||||
| TRMM | 0.39 | 0.53 | 0.58 | −0.47 | ||||||||
| GPCP V3.1 | −0.39 | 0.39 | 0.82 | 0.62 | ||||||||
| CHIRPS | 0.79 | −0.47 | ||||||||||
| ARC2 | −0.47 | 0.61 | 0.78 | −0.48 | ||||||||
| RFE | −0.53 | 0.57 | 0.59 | 0.77 | ||||||||
| CMAP | −0.45 | 0.65 | 0.56 | 0.60 | 0.73 | |||||||
| TAMSAT | −0.40 | 0.73 | 0.64 | |||||||||
| CMORPH | −0.59 | 0.50 | 0.55 | 0.46 | ||||||||
| PERSIANN | −0.51 | 0.40 | 0.60 | 0.57 | ||||||||
| CFSR | 0.68 | 0.71 | 0.50 | 0.65 | 0.47 | |||||||
| ERA5 | 0.53 | −0.57 | ||||||||||
| JRA55 | 0.38 | 0.57 | 0.37 | −0.40 | ||||||||
| MERRA2 | 0.50 | 0.47 | 0.48 | |||||||||
| NCEP II | 0.48 | −0.40 | 0.45 | −0.45 | −0.50 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicholson, S.E.; Klotter, D.A. Assessing the Reliability of Satellite and Reanalysis Estimates of Rainfall in Equatorial Africa. Remote Sens. 2021, 13, 3609. https://doi.org/10.3390/rs13183609
Nicholson SE, Klotter DA. Assessing the Reliability of Satellite and Reanalysis Estimates of Rainfall in Equatorial Africa. Remote Sensing. 2021; 13(18):3609. https://doi.org/10.3390/rs13183609
Chicago/Turabian StyleNicholson, Sharon E., and Douglas A. Klotter. 2021. "Assessing the Reliability of Satellite and Reanalysis Estimates of Rainfall in Equatorial Africa" Remote Sensing 13, no. 18: 3609. https://doi.org/10.3390/rs13183609
APA StyleNicholson, S. E., & Klotter, D. A. (2021). Assessing the Reliability of Satellite and Reanalysis Estimates of Rainfall in Equatorial Africa. Remote Sensing, 13(18), 3609. https://doi.org/10.3390/rs13183609