Reliable Estimates of Merchantable Timber Volume from Terrestrial Laser Scanning
Abstract
:1. Introduction
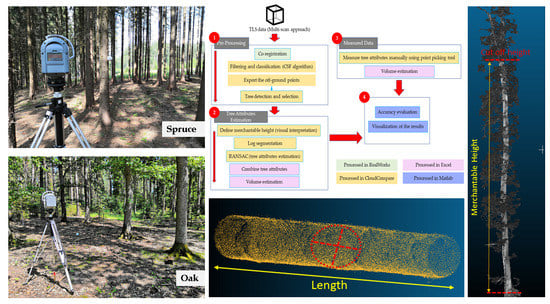
2. Materials and Methods
2.1. Characterization of the Study Area
2.2. TLS Data Acquisition and Pre-Processing
2.3. Filtering of Ground and Off-Ground Points
2.4. Sampling-Estimation and Measurement of Log Attributes
2.5. Validation
3. Results and Discussion
3.1. Considering the Full Merchantable Length
3.2. Considering Individual Logs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Liang, X.; Liang, Z.; Welham, C.; Li, W. Deriving Merchantable Volume in Poplar through a Localized Tapering Function from Non-Destructive Terrestrial Laser Scanning. Forests 2016, 7, 87. [Google Scholar] [CrossRef]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is field-measured tree height as reliable as believed—A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
- Wang, Y.; Pyörälä, J.; Liang, X.; Lehtomäki, M.; Kukko, A.; Yu, X.; Kaartinen, H.; Hyyppä, J. In situ biomass estimation at tree and plot levels: What did data record and what did algorithms derive from terrestrial and aerial point clouds in boreal forest. Remote Sens. Environ. 2019, 232, 111309. [Google Scholar] [CrossRef]
- Forsman, M.; Börlin, N.; Holmgren, J. Estimation of tree stem attributes using terrestrial photogrammetry with a camera rig. Forests 2016, 7, 61. [Google Scholar] [CrossRef]
- Kalliovirta, J.; Laasasenaho, J.; Kangas, A. Evaluation of the laser-relascope. For. Ecol. Manag. 2005, 204, 181–194. [Google Scholar] [CrossRef]
- Stereńczak, K.; Mielcarek, M.; Wertz, B.; Bronisz, K.; Zajączkowski, G.; Jagodziński, A.M.; Ochał, W.; Skorupski, M. Factors influencing the accuracy of ground-based tree height measurements for major European tree species. J. Environ. Manag. 2019, 231, 1284–1292. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Slavík, M. Assessment of Stem Volume on Plots Using Terrestrial Laser Scanner: A Precision Forestry Application. Sensors 2021, 21, 301. [Google Scholar] [CrossRef]
- Gaffrey, D.; Sloboda, B.; Matsumura, N. Representation of tree stem taper curves and their dynamic, using a linear model and the centroaffine transformation. J. For. Res. 1998, 3, 67–74. [Google Scholar] [CrossRef]
- Gong, J.R.; Zhang, X.S.; Huang, Y.M. Comparison of the performance of several hybrid poplar clones and their potential suitability for use in northern China. Biomass Bioenerg. 2011, 35, 2755–2764. [Google Scholar] [CrossRef]
- Chao, L.; Barclay, H.; Huang, S.M.; Hans, H.; Ghebremusse, S. Sensitivity of predictions of merchantable tree height, log production, and lumber recovery to tree taper. For. Chron. 2013, 89, 741–752. [Google Scholar]
- Rodríguez, F. Additively on nonlinear stem taper functions: A case for Corsican pine in Northern Spain. For. Sci. 2013, 59, 464–471. [Google Scholar]
- Subedi, N.; Sharma, M. Evaluating height–age determination methods for jack pine and black spruce plantations using stem analysis data. North. J. Appl. For. 2010, 27, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Zhang, Z.Q.; Sun, G.; Fang, X.R.; Zha, T.G.; McNulty, S.; Chen, J.Q. Response of ecosystem carbon fluxes to drought events in a poplar plantation in Northern China. For. Ecol. Manag. 2013, 300, 33–42. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Surový, P.; Kuželka, K. Accuracy of Structure from Motion models in comparison with terrestrial laser scanner for the analysis of DBH and height influence on error behaviour. J. For. Sci. 2016, 62, 357–365. [Google Scholar] [CrossRef] [Green Version]
- Cabo, C.; Del Pozo, S.; Rodríguez-Gonzálvez, P.; Ordóñez, C.; González-Aguilera, D. Comparing Terrestrial Laser Scanning (TLS) and Wearable Laser Scanning (WLS) for Individual Tree Modeling at Plot Level. Remote Sens. 2018, 10, 540. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level. Forests 2018, 9, 398. [Google Scholar] [CrossRef] [Green Version]
- Dassot, M.; Colin, A.; Santenoise, P.; Fournier, M.; Constant, T. Terrestrial laser scanning for measuring the solid wood volume, including branches, of adult standing trees in the forest environment. Electron. Agricult. 2012, 89, 86–93. [Google Scholar] [CrossRef]
- Iizuka, K.; Hayakawa, Y.S.; Ogura, T.; Nakata, Y.; Kosugi, Y.; Yonehara, T. Integration of Multi-Sensor Data to Estimate Plot-Level Stem Volume Using Machine Learning Algorithms–Case Study of Evergreen Conifer Planted Forests in Japan. Remote Sens. 2020, 12, 1649. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A. Accuracy Assessment of Total Stem Volume Using Close-Range Sensing: Advances in Precision Forestry. Forests 2021, 12, 717. [Google Scholar] [CrossRef]
- Momo Takoudjou, S.; Ploton, P.; Sonké, B.; Hackenberg, J.; Griffon, S.; De Coligny, F.; Kamdem, N.G.; Libalah, M.; Mofack, G.I.I.; Le Moguédec, G.; et al. Using terrestrial laser scanning data to estimate large tropical trees biomass and calibrate allometric models: A comparison with traditional destructive approach. Methods Ecol. Evol. 2018, 9, 905–916. [Google Scholar] [CrossRef]
- Gonzalez de Tanago, J.; Lau, A.; Bartholomeus, H.; Herold, M.; Avitabile, V.; Raumonen, P.; Martius, C.; Goodman, R.C.; Disney, M.; Manuri, S. Estimation of above-ground biomass of large tropical trees with terrestrial LiDAR. Methods Ecol. Evol. 2018, 9, 223–234. [Google Scholar] [CrossRef] [Green Version]
- Lau, A.; Bentley, L.P.; Martius, C.; Shenkin, A.; Bartholomeus, H.; Raumonen, P.; Malhi, Y.; Jackson, T.; Herold, M. Quantifying branch architecture of tropical trees using terrestrial LiDAR and 3D modelling. Trees 2018, 32, 1219–1231. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Sarría, A.; Velázquez-Martí, B.; Sajdak, M.; Martínez, L.; Estornell, J. Residual biomass calculation from individual tree architecture using terrestrial laser scanner and groundlevel measurements. Comput. Electron. Agric. 2013, 93, 90–97. [Google Scholar] [CrossRef]
- Yrttimaa, T.; Saarinen, N.; Luoma, V.; Tanhuanpaa, T.; Kankare, V.; Liang, X.L.; Hyyppa, J.; Holopainen, M.; Vastaranta, M. Detecting and characterizing downed dead wood using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2019, 151, 76–90. [Google Scholar] [CrossRef]
- Amiri, N.; Polewski, P.; Yao, W.; Krzystek, P.; Skidmore, A.K. Detection of Single Tree Stems in Forested Areas from High Density ALS Point Clouds Using 3d Shape Descriptors. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Wuhan, China, 18–22 September 2017; Volume IV-2/W4, pp. 35–42. [Google Scholar] [CrossRef] [Green Version]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree Stem and Height Measurements using Terrestrial Laser Scanning and the RANSAC Algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Zang, Y. Automated registration of dense terrestrial laser-scanning point clouds using curves. ISPRS J. Photogramm. Remote Sens. 2014, 3, 109–121. [Google Scholar] [CrossRef]
- Chen, C.; Yang, B. Dynamic occlusion detection and inpainting of in situ captured terrestrial laser scanning point clouds sequence. ISPRS J. Photogramm. Remote Sens. 2016, 119, 90–107. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of personal laser scanning in forestry inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef] [PubMed]
- Trimble RealWorks 10.2 User Guide. 2017. Available online: https://www.trimble.com/3d-laser-scanning/realworks.aspx (accessed on 12 October 2019).
- Girardeau-Montaut, D. Cloud Compare. 2017. Available online: http://www.danielgm.org (accessed on 19 December 2016).
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Gschwantner, T.; Alberdi, I.; Balázs, A.; Bauwens, S.; Bender, S.; Borota, D.; Bosela, M.; Bouriaud, O.; Cañellas, I.; Donis, J.; et al. Harmonisation of stem volume estimates in European National Forest Inventories. Ann. For. Sci. 2019, 76, 24. [Google Scholar] [CrossRef] [Green Version]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Baronti, L.; Alston, M.; Mavrakis, N.; Ghalamzan, E.A.M.; Castellani, M. Primitive Shape Fitting in Point Clouds Using the Bees Algorithm. Appl. Sci. 2019, 9, 5198. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Mayamanikandan, T.; Reddy, R.S.; Jha, C. Non-Destructive Tree Volume Estimation using Terrestrial Lidar Data in Teak Dominated Central Indian Forests. In Proceedings of the 2019 IEEE Recent Advances in Geoscience and Remote Sensing: Technologies, Standards and Applications (TENGARSS), Kochi, India, 17–20 October 2019; pp. 100–103. [Google Scholar]
- Pérez-Martín, E.; López-Cuervo Medina, S.; Herrero-Tejedor, T.; Pérez-Souza, M.A.; Aguirre de Mata, J.; Ezquerra-Canalejo, A. Assessment of Tree Diameter Estimation Methods from Mobile Laser Scanning in a Historic Garden. Forests 2021, 12, 1013. [Google Scholar] [CrossRef]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; De Tanago, J.G.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for terrestrial laser scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Vaaja, M.T.; Virtanen, J.-P.; Kurkela, M.; Lehtola, V.; Hyyppä, J.; Hyyppä, H. The effect of wind on tree stem parameter estimation using terrestrial laser scanning. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 8, 117–122. [Google Scholar] [CrossRef] [Green Version]










| Plot A | Plot B | |||
|---|---|---|---|---|
| Measured | Estimated | Measured | Estimated | |
| N | 15 | 15 | 15 | 15 |
| Range | 1.16 | 1.14 | 1.21 | 1.26 |
| Minimum | 0.58 | 0.61 | 0.19 | 0.18 |
| Maximum | 1.74 | 1.74 | 1.40 | 1.44 |
| Mean | 1.03 | 1.05 | 0.52 | 0.53 |
| Standard Error Mean | 0.09 | 0.09 | 0.09 | 0.09 |
| Standard Deviation | 0.35 | 0.35 | 0.34 | 0.34 |
| Variance | 0.12 | 0.12 | 0.11 | 0.12 |
| Skewness | 0.57 | 0.54 | 1.59 | 1.64 |
| Skewness Standard Error | 0.58 | 0.58 | 0.58 | 0.58 |
| Kurtosis | −0.62 | −0.68 | 2.32 | 2.71 |
| Kurtosis Standard Error | 1.12 | 1.12 | 1.12 | 1.12 |
| Negative Ranks | Positive Ranks | Z | Asymp. Sig. (2-Tailed) |
|---|---|---|---|
| 7.0000 | 8.0000 | −1.306 * | 0.191 |
| Mean | Standard Deviation | Standard Error Mean | 95% CID 1 | t | df | Sig. (2-Tailed) | |
|---|---|---|---|---|---|---|---|
| Lower | Upper | ||||||
| −0.0177 | 0.0221 | 0.0057 | −0.0299 | −0.0055 | −3.1040 | 14 | 0.0080 |
| Metric | Plot A | Plot B | Metric | Plot A | Plot B |
|---|---|---|---|---|---|
| MAD | 0.02 | 0.02 | MAPE | 2.27 | 3.86 |
| MSE | 0.00 | 0.00 | BIAS | 0.02 | 0.01 |
| RMSE | 0.03 | 0.02 | BIAS% | 1.68 | 1.49 |
| RMSE% | 2.68 | 4.09 | MAE | 0.02 | 0.02 |
| % of accuracy | 97.73 | 96.14 | N | 15.00 | 15.00 |
| Length | Estimated Diameter | Measured Diameter | |||||
|---|---|---|---|---|---|---|---|
| CC 1 | Sig. | CC 1 | Sig. | CC 1 | Sig. | ||
| Plot A | Bias | −0.814 | 0 | −0.618 | 0 | −0.617 | 0 |
| Absolute Residuals | 0.610 | 0 | 0.122 | 0.157 | 0.103 | 0.23 | |
| Plot B | Bias | −0.698 | 0 | −0.635 | 0 | −0.658 | 0 |
| Absolute Residuals | 0.367 | 0.009 | 0.354 | 0.012 | 0.332 | 0.02 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panagiotidis, D.; Abdollahnejad, A. Reliable Estimates of Merchantable Timber Volume from Terrestrial Laser Scanning. Remote Sens. 2021, 13, 3610. https://doi.org/10.3390/rs13183610
Panagiotidis D, Abdollahnejad A. Reliable Estimates of Merchantable Timber Volume from Terrestrial Laser Scanning. Remote Sensing. 2021; 13(18):3610. https://doi.org/10.3390/rs13183610
Chicago/Turabian StylePanagiotidis, Dimitrios, and Azadeh Abdollahnejad. 2021. "Reliable Estimates of Merchantable Timber Volume from Terrestrial Laser Scanning" Remote Sensing 13, no. 18: 3610. https://doi.org/10.3390/rs13183610
APA StylePanagiotidis, D., & Abdollahnejad, A. (2021). Reliable Estimates of Merchantable Timber Volume from Terrestrial Laser Scanning. Remote Sensing, 13(18), 3610. https://doi.org/10.3390/rs13183610