Improving the Robustness of the MTI-Estimated Mining-Induced 3D Time-Series Displacements with a Logistic Model
Abstract
:1. Introduction
2. Methodology
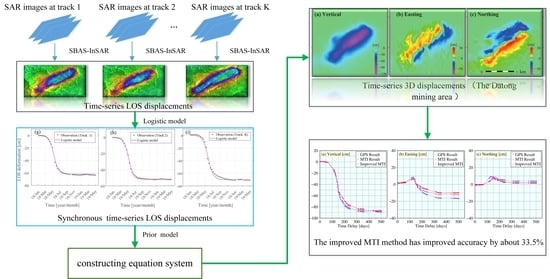
2.1. Overview of the Track-by-Track MTI Method
2.2. Development of the Improved Fused-Track MTI Method
2.2.1. Synchronization of Multi-Track Time-Series LOS Displacements Using the Logistic Model
2.2.2. Fused-Track-Based Estimation of 3D Time-Series (TS) Displacements
3. Experiments and Results
3.1. Study Area and SAR Dataset
3.2. Retrieval of Multi-Track Time-Series LOS Displacements
3.3. Synchronization of the Multi-Track Time-Series LOS Displacements
3.4. Estimation of Mining-Induced Time-Series 3D Displacements
3.5. Accuracy Evaluation
4. Discussion
4.1. Comparison of the Robustness of the Improved MTI and MTI Methods
4.1.1. Simulation Analysis
4.1.2. Real Data Analysis
4.2. Capability of the Logistic Model for Modeling Mining-Induced LOS Displacements
4.3. Selection of the Models to Interpolate Multi-Track LOS Displacements
4.4. Efficiency of the QL+GN Algorithm for Estimating the Parameters of the Logistic Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- IEA. Coal 2019; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Cando Jacome, M.; Martinez-Grana, A.M.; Valdes, V. Detection of Terrain Deformations Using InSAR Techniques in Relation to Results on Terrain Subsidence (Ciudad de Zaruma, Ecuador). Remote Sens. 2020, 12, 1598. [Google Scholar] [CrossRef]
- Vu Khac, D.; Thanh Dong, N.; Ngoc Hung, D.; Thi Loi, D.; Xuan Vinh, D.; Weber, C. Land subsidence induced by underground coal mining at Quang Ninh, Vietnam: Persistent scatterer interferometric synthetic aperture radar observation using Sentinel-1 data. Int. J. Remote Sens. 2021, 42, 3563–3582. [Google Scholar] [CrossRef]
- Diao, X.P.; Bai, Z.H.; Wu, K.; Zhou, D.W.; Li, Z.L. Assessment of mining-induced damage to structures using InSAR time series analysis: A case study of Jiulong Mine, China. Environ. Earth Sci. 2018, 77, 166. [Google Scholar] [CrossRef]
- Bateson, L.; Cigna, F.; Boon, D.; Sowter, A. The application of the Intermittent SBAS (ISBAS) InSAR method to the South Wales Coalfield, UK. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 249–257. [Google Scholar] [CrossRef] [Green Version]
- Gee, D.; Bateson, L.; Sowter, A.; Grebby, S.; Novellino, A.; Cigna, F.; Marsh, S.; Banton, C.; Wyatt, L. Ground Motion in Areas of Abandoned Mining: Application of the Intermittent SBAS (ISBAS) to the Northumberland and Durham Coalfield, UK. Geosciences 2017, 7, 85. [Google Scholar] [CrossRef] [Green Version]
- Milczarek, W.; Kopec, A.; Glabicki, D.; Bugajska, N. Induced Seismic Events-Distribution of Ground Surface Displacements Based on InSAR Methods and Mogi and Yang Models. Remote Sens. 2021, 13, 1451. [Google Scholar] [CrossRef]
- Malinowska, A.A.; Witkowski, W.T.; Hejmanowski, R.; Chang, L.; van Leijen, F.J.; Hanssen, R.F. Sinkhole occurrence monitoring over shallow abandoned coal mines with satellite-based persistent scatterer interferometry. Eng. Geol. 2019, 262, 105336. [Google Scholar] [CrossRef]
- Ren, H.; Feng, X. Calculating vertical deformation using a single InSAR pair based on singular value decomposition in mining areas. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102115. [Google Scholar] [CrossRef]
- Fan, H.; Wang, L.; Wen, B.; Du, S. A New Model for three-dimensional Deformation Extraction with Single-track InSAR Based on Mining Subsidence Characteristics. Int. J. Appl. Earth Obs. Geoinf. 2021, 94, 102223. [Google Scholar] [CrossRef]
- Zheng, M.; Deng, K.; Fan, H.; Huang, J. Monitoring and analysis of mining 3D deformation by multi-platform SAR images with the probability integral method. Front. Earth Sci. 2019, 13, 169–179. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Wang, Y.; Wu, L. Use of SAR/InSAR in Mining Deformation Monitoring, Parameter Inversion, and Forward Predictions: A Review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 71–90. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Feng, G.; Wang, Q.; Hu, J.; Wang, C. Deriving time-series three-dimensional displacements of mining areas from a single-geometry InSAR dataset. J. Geod. 2018, 92, 529–544. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, Z.F.; Zhu, J.J.; Hu, J.; Wang, Y.J.; Li, P.X.; Chen, G.L. Retrieving three-dimensional displacement fields of mining areas from a single InSAR pair. J. Geod. 2015, 89, 17–32. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.; Ding, X.; Zhu, J.; Zhang, L.; Sun, Q. Resolving three-dimensional surface displacements from InSAR measurements: A review. Earth-Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Z.; Li, Z.; Zhu, J.; Wu, L. Fusing adjacent-track InSAR datasets to densify the temporal resolution of time-series 3-D displacement estimation over mining areas with a prior deformation model and a generalized weighting least-squares method. J. Geod. 2020, 94, 47. [Google Scholar] [CrossRef]
- Osmanoğlu, B.; Sunar, F.; Wdowinski, S.; Cabral-Cano, E. Time series analysis of InSAR data: Methods and trends. ISPRS J. Photogramm. Remote Sens. 2016, 115, 90–102. [Google Scholar] [CrossRef]
- Lanari, R.; Lundgren, P.; Manzo, M.; Casu, F. Satellite radar interferometry time series analysis of surface deformation for Los Angeles, California. Geophys. Res. Lett. 2004, 31, L23613. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arikan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514, 1–13. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcan Alcedo, Galapagos. J. Geophys. Res.-Solid Earth 2007, 112, B07407. [Google Scholar] [CrossRef] [Green Version]
- Sousa, J.J.; Ruiz, A.M.; Hanssen, R.F.; Bastos, L.; Gil, A.J.; Galindo-Zaldivar, J.; de Galdeano, C.S. PS-InSAR processing methodologies in the detection of field surface deformation Study of the Granada basin (Central Betic Cordilleras, southern Spain). J. Geodyn. 2010, 49, 181–189. [Google Scholar] [CrossRef]
- Tizzani, P.; Berardino, P.; Casu, F.; Euillades, P.; Manzo, M.; Ricciardi, G.P.; Zeni, G.; Lanari, R. Surface deformation of Long Valley Caldera and Mono Basin, California, investigated with the SBAS-InSAR approach. Remote Sens. Environ. 2007, 108, 277–289. [Google Scholar] [CrossRef]
- Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the epicentral area of the 1999 Mw7. 1 Hector Mine earthquake, California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Xu, B.; Li, Z.; Wu, L.; Zhu, J. Prediction of Mining-Induced Kinematic 3-D Displacements From InSAR Using a Weibull Model and a Kalman Filter. IEEE Trans. Geosci. Remote Sens. 2021, 1, 1–12. [Google Scholar] [CrossRef]
- Kratzsch, I.H. Mining Subsidence Engineering; Environmental Geology and Water Sciences: New York, NY, USA, 1983. [Google Scholar]
- Zhang, W.Z.; Zou, Y.F.; Ren, X.F. Research on logistic model in forecasting subsidence single-point during mining. J. Min. Saf. Eng. 2009, 26, 486–489. [Google Scholar]
- Mao, W.-L.; Ma, W.-J.; Chien, Y.-R.; Ku, C.-H. New Adaptive All-pass Based Notch Filter for Narrowband/FM Anti-jamming GPS Receivers. Circuits Syst. Signal Process. 2011, 30, 527–542. [Google Scholar] [CrossRef]
- Worthen, J.; Stadler, G.; Petra, N.; Gurnis, M.; Ghattas, O. Towards adjoint-based inversion for rheological parameters in nonlinear viscous mantle flow. Phys. Earth Planet. Inter. 2014, 234, 23–34. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Yi, H.; Hu, J.; Feng, G. Deriving Dynamic Subsidence of Coal Mining Areas Using InSAR and Logistic Model. Remote Sens. 2017, 9, 125. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.S. Surface Subsidence Engineering: Theory and Practice; CSIRO Publishing: Clayton, VIC, Australia, 2020. [Google Scholar]
- Yang, C.; Lu, Z.; Zhang, Q.; Liu, R.; Ji, L.; Zhao, C. Ground deformation and fissure activity in Datong basin, China 2007-2010 revealed by multi-track InSAR. Geomat. Nat. Hazards Risk 2019, 10, 465–482. [Google Scholar] [CrossRef]
- Zhao, C.; Lu, Z.; Zhang, Q.; Yang, C.; Zhu, W. Mining collapse monitoring with SAR imagery data: A case study of Datong mine, China. J. Appl. Remote Sens. 2014, 8, 083574. [Google Scholar] [CrossRef]
- Zhi-ying, H. Movement law of coal mining subsidence surface ground in Datong Mining Area. Coal Sci. Technol. 2004, 2, 50–52. [Google Scholar] [CrossRef]
- Xu, B.; Li, Z.; Zhu, Y.; Shi, J.; Feng, G. Kinematic Coregistration of Sentinel-1 TOPSAR Images Based on Sequential Least Squares Adjustment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3083–3093. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
- Fu, P.; Ge, Y.; Ma, C.; Jia, X.; Shan, X.; Li, F.; Zhang, X. A Study of Land Subsidence by Radar Remote Sensing at Datong Jurassic & Carboniferous Period Coalfield. In Proceedings of the 2009 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009; Volume 942, pp. 1–4. [Google Scholar] [CrossRef]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Diao, X.; Wu, K.; Hu, D.; Li, L.; Zhou, D. Combining differential SAR interferometry and the probability integral method for three-dimensional deformation monitoring of mining areas. Int. J. Remote Sens. 2016, 37, 5196–5212. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Hu, J.; Wang, Y.J.; Chen, G.L. InSAR-Based Model Parameter Estimation of Probability Integral Method and Its Application for Predicting Mining-Induced Horizontal and Vertical Displacements. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4818–4832. [Google Scholar] [CrossRef]
- Hanssen, R.; Bamler, R. Evaluation of interpolation kernels for SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1999, 37, 318–321. [Google Scholar] [CrossRef]
- Ronchin, E.; Masterlark, T.; Dawson, J.; Saunders, S.; Molist, J.M. Imaging the complex geometry of a magma reservoir using FEM-based linear inverse modeling of InSAR data: Application to Rabaul Caldera, Papua New Guinea. Geophys. J. Int. 2017, 209, 1746–1760. [Google Scholar] [CrossRef] [Green Version]
- Zeide, B. Analysis of growth equations. For. Sci. 1993, 39, 594–616. [Google Scholar] [CrossRef]










| Satellite Characteristics | Track 040 | Track 113 | Track 120 |
|---|---|---|---|
| Orbit direction | Ascending | Ascending | Descending |
| Number of images | 41 | 43 | 41 |
| Time spanning | 8 January 2018–27 May 2019 | 1 January 2018–20 May 2019 | 7 January 2018–26 May 2019 |
| Incident angle | 33.67° | 43.77° | 43.9° |
| Heading angle | −10.5° | −9.2° | −170.7° |
| Method | Vertical [cm] | Easting [cm] | Northing [cm] |
|---|---|---|---|
| Improved MTI | 1.4 | 2.8 | 1.7 |
| MTI | 2.3 | 3.5 | 2.9 |
| Improvement | 39.1% | 20.0% | 41.4% |
| Method | Parameters | RMSE (cm) | Time Cost (Seconds) | ||
|---|---|---|---|---|---|
| a | b | c | |||
| QL+GN | 900.03 | 0.037 | −66.60 | 0.61 | 0.1 |
| GA+SA | 900.04 | 0.037 | −66.60 | 0.62 | 2.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Yang, Z.; Wu, L.; Qiao, S. Improving the Robustness of the MTI-Estimated Mining-Induced 3D Time-Series Displacements with a Logistic Model. Remote Sens. 2021, 13, 3782. https://doi.org/10.3390/rs13183782
Shi J, Yang Z, Wu L, Qiao S. Improving the Robustness of the MTI-Estimated Mining-Induced 3D Time-Series Displacements with a Logistic Model. Remote Sensing. 2021; 13(18):3782. https://doi.org/10.3390/rs13183782
Chicago/Turabian StyleShi, Jiancun, Zefa Yang, Lixin Wu, and Siyu Qiao. 2021. "Improving the Robustness of the MTI-Estimated Mining-Induced 3D Time-Series Displacements with a Logistic Model" Remote Sensing 13, no. 18: 3782. https://doi.org/10.3390/rs13183782
APA StyleShi, J., Yang, Z., Wu, L., & Qiao, S. (2021). Improving the Robustness of the MTI-Estimated Mining-Induced 3D Time-Series Displacements with a Logistic Model. Remote Sensing, 13(18), 3782. https://doi.org/10.3390/rs13183782