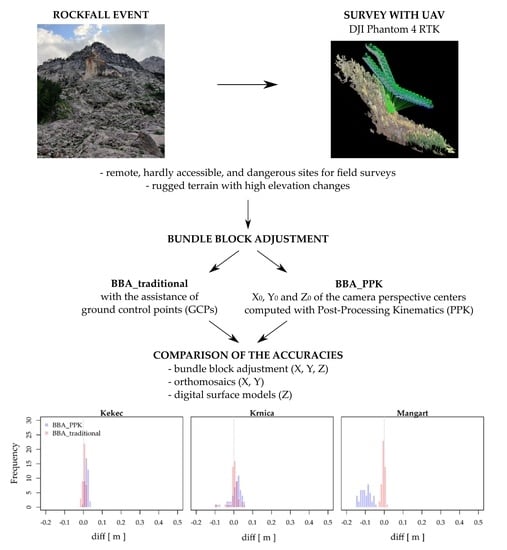
Accuracy Assessment of UAV-Photogrammetric-Derived Products Using PPK and GCPs in Challenging Terrains: In Search of Optimized Rockfall Mapping
Abstract
:1. Introduction
1.1. Challenges of UAV Photogrammetric Georeferencing
1.2. Previous Work on UAV Images Georeferencing without GCPs
1.3. Aim of the Study
2. Materials and Methods
2.1. Study Sites
2.2. Setting Up Ground Control and Verification Points
2.3. Flight Planning and Acquisition of Data with UAV
2.4. Data Processing
2.5. Accuracy Assessment of Bundle Block Adjustment, Orthomosaic and Digital Surface Model
3. Results
3.1. Assessing the Accuracy of Bundle Block Adjustment
3.2. Assessing Accuracy of Orthomosaic
3.3. Assessing Accuracy of DSM
3.4. Spatial Distribution of X, Y and Z Differences
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Authors | UAV | Study Area | GEO | Flight Configuration | Bundle Block Adjustment | Orthomosaic | DSM | |
|---|---|---|---|---|---|---|---|---|
| Horizontal Accuracy (m) | Vertical Accuracy (m) | Horizontal Accuracy (m) | Vertical Accuracy (m) | |||||
| Mian et al., 2015 | microdrone md4-1000 quadcopter with RTK GNSS | flat agricultural area | RTK |
| 0.03 | 0.11 | 0.05 | / |
| Fazeli et al., 2016 | UAV RTK platform | agricultural, semi-industrial area | RTK |
| 0.164 | 0.235 | / | / |
| Mian et al., 2016 | microdrone md4-1000 quadcopter with RTK GNSS | railway corridor | RTK |
| / | / | 0.201 | 0.767 |
| Padró et al., 2019 | octocopter DJI S100 with RGB camera (PPK2) and DJI S900 with multispectral camera (MicaSense RedEdge)—PPK1 | agricultural area (crops, abandoned vineyards, vegetation) | PPK1: single freq. |
| / | / | 0.256 | 0.238 |
| PPK2: dual freq. | / | / | 0.036 | 0.036 | ||||
| Wiącek and Pyka, 2019 | FlyTech UAV BIRDIE | residential city area | PPK | Flying variants:
| / | / | 0.030–0.040 | 0.030–0.050 |
| Zhang et al., 2019 | custom-built Hexacopter and DJI Phantom 3 Advanced, equipped with multi-GNSS RTK receiver | agricultural area | PPK |
| / | / |
|
|
| Ekaso et al., 2020 | DJI Matrice 600 Pro with RTK | flatlands | RTK |
|
|
| / | / |
| Hugenholtz et al., 2016 | senseFly eBee RTK | gravel quarry, non-vegetated active pit | RTK |
| / | / | 0.025 | 0.100 |
| Benassi et al., 2017 | senseFly eBee RTK | campus area (parking lots, green areas, different buildings) | RTK |
| / | / | 0.030 | 0.120 |
| Forlani et al., 2018 | senseFly eBee RTK | campus area with buildings, roads, car parks and meadows | RTK |
| 0.025 | 0.095 | / | / |
| NRTK | 0.042 | 0.126 | / | / | ||||
| Rabah et al., 2018 | senseFly eBee RTK | industrial area | RTK |
| 0.034 | 0.029 | / | / |
| Forlani et al., 2019 | senseFly eBee RTK and DJI Phantom 4 RTK | road bridge and riverbed | RTK |
|
|
| / | / |
| Tomaštík et al., 2019 | senseFly eBee RTK | rugged forested area with valleys and ridges | PPK |
|
|
|
|
|
| Tufarolo et al., 2019 | senseFly eBee RTK | morphologically complex (quarry) area with extremely steep slopes | NRTK |
| 0.830 | 1.880 | / | / |
| Forlani et al., 2020 | DJI Phantom 4 RTK | grassed sports area | RTK |
| 0.020–0.040 | 0.020–0.050 | / | / |
| PPK | 0.010–0.040 | 0.010–0.060 | / | / | ||||
| Štroner et al., 2020 | DJI Phantom 4 RTK | urban and rural area | RTK |
| 0.044 | 0.103 | / | / |
| Taddia et al., 2020 | DJI Phantom 4 RTK | building’s façade | RTK |
|
|
| / | / |
| NRTK |
|
| / | / | ||||
| Teppati Losè et al., 2020 | DJI Phantom 4 RTK | archeological/architectural site | NRTK |
| 0.057 | 0.068 | / | / |
| PPK | 0.006 | 0.727 | / | / | ||||
| Teppati Losè et al., 2020b | DJI Phantom 4 RTK | gardens | NRTK |
|
|
| / | / |
| PPK |
|
|
| / | / | |||
| DRTK |
|
|
| / | / | |||
| Taddia et al., 2020 | DJI Phantom 4 RTK | coastal area | PPK |
|
|
| ||
| Štroner et al., 2021 | DJI Phantom 4 RTK UAV | urban and rural area | RTK |
| <0.030 | <0.053 | / | / |
References
- Giordian, D.; Manconi, A.; Facello, A.; Baldo, M.; dell’Anese, F.; Allasia, P.; Dutto, F. Brief communication: The use of unmanned aerial vehicle in a rockfall emergency scenario. Nat. Hazards Earth Syst. Sci. 2015, 15, 163–169. [Google Scholar] [CrossRef] [Green Version]
- Saroglou, C.; Asteriou, P.; Zekkos, D.; Tsiambaos, G.; Clark, M.; Manousakis, J. UAV-based mapping, back analysis and trajectory modeling of a coseismic rockfall in Lefkada island, Greece. Nat. Hazards Earth Syst. Sci. 2018, 18, 321–333. [Google Scholar] [CrossRef] [Green Version]
- Sarro, R.; Riquelme, A.; Garcia-Davalillo, J.C.; Mateos, R.M.; Tomás, R.; Pasto, J.L.; Cano, M.; Herrera, G. Rockfall simulation based on UAV photogrammetry data obtained during and emergency declaration: Application at a cultural heritage site. Remote Sens. 2018, 10, 1923. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, J.; Macciotta, R.; Hendry, M.T.; Roustaei, M.; Gräpel, C.; Skirrow, R. UAVs for monitoring, investigation, and mitigation design of a rock slope with multiple failure mechanisms—a case study. Landslides 2020, 17, 2027–2040. [Google Scholar] [CrossRef]
- Danzi, M.; Di Crescenzo, G.; Ramondini, M.; Santo, A. Use of unmanned aerial vehicles (UAVs) for photogrammetric surveys in rockfall instability studies. Rend. Online Soc. Geol. Ital. 2013, 24, 82–85. [Google Scholar]
- Sotier, B.; Adams, M.; Lechner, V. UAV-based natural hazard management in high-alpine terrain—Case studies from Austria. Geophys. Res. Abstr. 2015, 17, EGU2015–EGU13611. [Google Scholar]
- Salvini, R.; Mastrorocco, G.; Esposito, G.; Di Bartolo, S.; Coggan, J.; Vanneschi, C. Use of a remotely piloted aircraft system for hazard assessment in a rocky mining area (Lucca, Italy). Nat. Hazards Earth Syst. Sci. 2018, 18, 287–302. [Google Scholar] [CrossRef] [Green Version]
- Vanneschi, C.; Di Camillo, M.; Aiello, E.; Bonciani, F.; Salvini, R. SfM-MVS photogrammetry for rockfall analysis and hazard assessment along the ancient roman via flamina road at the Furlo Gorge. ISPRS Int. J. Geoinf. 2019, 8, 325. [Google Scholar] [CrossRef] [Green Version]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. 2014, 92, 79–97. [Google Scholar] [CrossRef] [Green Version]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Giordian, D.; Manconi, A.; Remondino, F.; Nex, F. Use of unmanned aerial vehicles in monitoring and application and management of natural hazards. Geomat. Nat. Haz. Risk 2017, 8, 1–4. [Google Scholar] [CrossRef]
- Buill, F.; Núñez-Andrés, M.A.; Lantada, N.; Prades, A. Comparing of Photogrammetric Techniques for rockfalls monitoring. In Proceedings of the Word Multidisciplinary Earth Sciences Symposium (WMESS 2016), Prague, Czech Republic, 5–9 September 2016. [Google Scholar] [CrossRef] [Green Version]
- Gomez, C.; Purdie, H. UAV-based photogrammetry and geocomputing for hazards and disaster risk monitoring—A review. Geoenviron. Disasters 2016, 3, 23. [Google Scholar] [CrossRef] [Green Version]
- Salvini, R.; Francioni, M.; Riccucci, S.; Bonciani, F.; Callegari, I. Photogrammetry and laser scanning for analyzing slope stability and rock fall runout along the Domodossola-Iselle railway, the Italian Alps. Geomorphology 2013, 185, 110–122. [Google Scholar] [CrossRef]
- Kim, D.H.; Gratchev, I.; Berends, J.; Balasubramaniam, A. Calibration of restitution coefficients using rockfall simulations based on 3D photogrammetry model: A case study. Nat. Hazards 2015, 78, 1931–1946. [Google Scholar] [CrossRef] [Green Version]
- Lato, M.J.; Hutchinson, D.J.; Gauthier, D.; Edwards, T.; Ondercin, M. Comparison of airborne laser scanning, terrestrial laser scanning, and terrestrial photogrammetry for mapping differential slope change in mountainous terrain. Can. Geotech. J. 2015, 52, 129–140. [Google Scholar] [CrossRef]
- Manousakis, J.; Zekkos, D.; Saroglou, H.; Clark, M. Comparison of UAV-enabled photogrammetry-based 3D point clouds and interpolated DSMs of sloping terrain for rockfall hazard analysis. In Proceedings of the International Archives of the Photo-grammetry, Remote Sensing and Spatial Information Sciences, 11th 3D Geoinfo Conference, Athens, Greece, 20–21 October 2016; Volume XLII-2/W2, pp. 71–77. [Google Scholar]
- Thoeni, K.; Guccione, D.; Santise, M.; Giacomini, A.; Roncella, R.; Forlani, G. The potential of low-cost RPAS multi-view re-construction of sub-vertical rock faces. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, XLI-B5, 909–916. [Google Scholar] [CrossRef] [Green Version]
- Albarelli, D.S.N.A.; Mavrouli, O.C.; Nyktas, P. Identification of potential rockfall sources using UAV-derived point cloud. Bull. Eng. Geol. Environ. 2021, 80, 6539–6561. [Google Scholar] [CrossRef]
- Santangelo, M.; Alvioli, M.; Baldo, M.; Cardinali, M.; Giordian, D.; Guzzetti, F.; Marchesini, I.; Reichenbach, P. Brief communication: Remotely piloted aircraft systems for rapid emergency response: Road exposure to rockfall in Villanova di Accumoli. Nat. Hazards Earth Syst. Sci. 2019, 19, 325–335. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Zhang, Z.; Wang, C.; Zhu, C.; Ren, Y. Multistep slope stability analysis based on unmanned aerial vehicle photogrammetry. Environ. Earth Sci. 2019, 78, 260. [Google Scholar] [CrossRef]
- Koukouvelas, I.K.; Nikolakopoulos, K.G.; Zygouri, V.; Kyriou, A. Post-seismic monitoring of cliff mass wasting using an unmanned aerial vehicle and field data at Egremni, Lefkada Island, Greece. Geomorphology 2020, 367, 107036. [Google Scholar] [CrossRef]
- Macciotta, R.; Gräpel, C.; Skirrow, R. Fragmented rockfall volume distribution from photogrammetry-based structural mapping and discrete fracture networks. Appl. Sci. 2020, 10, 6977. [Google Scholar] [CrossRef]
- Gabrlik, P. The use of direct georeferencing in aerial photogrammetry with micro UAV. IFAC-Pap. 2015, 48, 380–385. [Google Scholar] [CrossRef]
- Rabah, M.; Basiouny, M.; Ghanem, E.; Elhadry, A. Using RTK and VRS in direct geo-referencing of the UAV imagery. NRIAG J. Astron. Geophys. 2018, 7, 220–226. [Google Scholar] [CrossRef] [Green Version]
- Cramer, M.; Stallmann, D.; Haala, N. Direct geo-referencing using GPS/inertial exterior orientations for photogrammetric applications. In Proceedings of the International Archives of Photogrammetry and Remote Sensing, Amsterdam, The Netherlands, 16–23 July 2020; Volume 33, pp. 198–205. [Google Scholar]
- Forlani, G.; Diotri, F.; di Cella, U.M.; Roncella, R. Indirect UAV strip georeferencing by on-board GNSS data under poor satellite coverage. Remote Sens. 2019, 11, 1765. [Google Scholar] [CrossRef] [Green Version]
- Tomaštík, J.; Mokroš, M.; Surový, P.; Grznárová, A.; Merganič, J. UAV RTK/PPK method—An optimal solution for mapping inaccessible forested areas? Remote Sens. 2019, 11, 721. [Google Scholar] [CrossRef] [Green Version]
- Cledat, E.; Jospin, L.V.; Cucci, D.A.; Skaloud, J. Mapping quality prediction for RTK/PPK-equipped micro-drones operating in complex natural environment. ISPRS J. Photogramm. 2020, 167, 24–38. [Google Scholar] [CrossRef]
- Sanz-Ablanedo, E.; Chandle, J.H.; Rodríguez-Pérez, J.; Ordóñez, C. Accuracy of unmanned aerial vehicle (UAV) and SfM photogrammetry survey as a function of the number and location of ground control points used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef] [Green Version]
- Teppati Losè, L.; Chiabrando, F.; Giulio Tonolo, F. Are measured ground control points still required in UAV based large scale mapping? Assessing the positional accuracy of an RTK multi-roto platform. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2020, XLIII-B1-2020, 507–514. [Google Scholar] [CrossRef]
- Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Morra di Cella, U.; Roncella, R.; Santise, M. Testing accuracy and repeatability of UAV blocks oriented with GNSS-supported aerial triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef] [Green Version]
- Wiącek, P.; Pyka, K. The test field for UAV accuracy assessments. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2019, XLI-1/W2, 67–73. [Google Scholar] [CrossRef] [Green Version]
- DJI Phantom 4 RTK. Available online: https://www.dji.com/si/phantom-4-rtk (accessed on 18 April 2021).
- senseFly 2021. Available online: https://www.sensefly.com/ (accessed on 11 May 2021).
- Hugenholtz, C.; Brown, O.; Walker, J.; Barchyn, T.; Nesbit, P.; Kucharczyk, M.; Myshak, S. Spatial accuracy of UAV-derived orthoimagery and topography: Comparing photogrammetric models processed with direct geo-referencing and ground control points. Geomatica 2016, 70, 21–30. [Google Scholar] [CrossRef]
- Padró, J.-C.; Muñoz, F.-J.; Planas, J.; Pons, X. Comparison of four UAV georeferencing methods for environmental monitoring purposes focusing on the combined use with airborne and satellite remote sensing platforms. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 130–140. [Google Scholar] [CrossRef]
- Mian, O.; Luter, J.; Lipa, G.; Hutton, J.J.; Gavelle, E.; Borghini, S. Direct georeferencing on small unmanned aerial platforms for improved reliability and accuracy of mapping without the need for ground control points. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XL-1/W4, Proceedings of the International Conference on Unmanned Aerial Vehicles in Geomatics, Toronto, Canada, 30 August–2 September 2015; ISPRS: Toronto, ON, Canada, 2015; pp. 397–402. [Google Scholar]
- Fazeli, H.; Samadzadegan, F.; Dadrasjavan, F. Evaluating the potential of RTK-UAV for automatic point cloud generation in 3D rapid mapping. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XLI-B6, XXIII Congress, Prague, Czech Republic, 12–19 July 2016; ISPRS: Prague, Czech Republic, 2016; pp. 221–226. [Google Scholar]
- Zhang, H.; Aldana-Jague, E.; Clapuyt, F.; Wilken, F.; Vanacker, V.; Van Oost, K. Evaluating the potential of post-processing kinematic (PPK) georeferencing for UAV-based structure-from-motion (SfM) photogrammetry and surface change detection. Earth Surf. Dynam. 2019, 7, 807–827. [Google Scholar] [CrossRef] [Green Version]
- Ekaso, D.; Nex, F.; Kerle, N. Accuracy assessment of real-time kinematics (RTK) measurements in unmanned aerial vehicles (UAV) for direct geo-referencing. Geo Spat. Inf. Sci. 2020, 23, 165–181. [Google Scholar] [CrossRef] [Green Version]
- Mian, O.; Luter, J.; Lipa, G.; Hutton, J.J.; Gavelle, E.; Borghini, S. Accuracy assessment of direct georeferencing for photogrammetric applications on small unmanned aerial platforms. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XL-3/W4, Proceedings of the EuroCOW 2016, the European Calibration and Orientation Workshop, Lausanne, Switzerland, 10–12 February 2016; Applanix: Richmond Hill, ON, Canada, 2016; pp. 77–83. [Google Scholar]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; Morra di Cella, U.; Roncella, R.; Santise, M. Quality assessment of DSMs produced from UAV flights georeferenced with on-board RTK positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef] [Green Version]
- Forlani, G.; Diotri, F.; Morra di Cella, U.; Roncella, R. UAV block georeferencing and control by on-board GNSS data. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2020, XLIII-B2-2020, 9–16. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Reindl, R.; Seidl, J.; Brouček, J. Evaluation of the georeferencing accuracy of a photogrammetric model using a quadrocopter with onboard GNSS RTK. Sensors 2020, 20, 2318. [Google Scholar] [CrossRef] [Green Version]
- Taddia, Y.; González-García, L.; Zambello, E.; Pellegrinelli, A. Quality assessment of photogrammetric models for façade and building reconstruction using DJI Phantom 4 RTK. Remote Sens. 2020, 12, 3144. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry using UAV-mounted GNSS RTK georeferencing strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Tufarolo, E.; Vanneschi, C.; Casella, M.; Salvini, R. Evaluation of camera positions and ground control points quality in a GNSS-RTK based UAV survey: Preliminary results from a practical test in morphological very complex areas. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XLII-2/W13; Proceedings of the Geospatial Week 2019, Enschede, The Netherlands, 10–14 June 2019; ISPRS: Enschede, The Netherlands, 2019; pp. 637–641. [Google Scholar]
- Teppati Losè, L.; Chiabrando, F.; Tonolo, F.G. Boosting the timeliness of UAV large scale mapping. Direct georeferencing approaches: Operational strategies and best practices. ISPRS Int. J. Geo.-Inf. 2020, 9, 578. [Google Scholar] [CrossRef]
- Taddia, Y.; Stecchi, F.; Pellegrini, A. Coastal mapping using DJI Phantom 4 RTK in post-processing kinematic mode. Drones 2020, 4, 9. [Google Scholar] [CrossRef] [Green Version]
- Caroti, G.; Zaragoza, M.-E.; Piemonte, A. Accuracy assessment in structure from motion 3D reconstruction from UAV-born images The influence of the data processing methods. In International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XL-1/W4, Proceedings of the International Conference on Unmanned Aerial Vehicles in Geomatics, Toronto, Canada, 30 August–2 September 2015; ISPRS: Toronto, ON, Canada, 2015; pp. 103–109. [Google Scholar]
- Jurkovšek, B. Tolmač Listov Beljak in Ponteba: Osnovna Geološka Karta, SFRJ 1:100,000; Zvezni Geološki Zavod: Belgrade, Serbia, 1987; p. 55. [Google Scholar]
- Placer, L. Osnovne tektonske razčlenitve Slovenije. Geologija 2008, 51, 205–217. [Google Scholar] [CrossRef]
- Jurkovšek, B.; Šribar, L.; Ogorelec, B.; Kolar-Jurkovšek, T. Pelagic Jurassic and Cretaceous beds in the western part of the Julian Alps. Geologija 2020, 31, 285–328. [Google Scholar]
- ArcGIS Pro 2.7.3, Esri. Available online: https://www.esri.com/en-us/arcgis/products/arcgis-pro/resources (accessed on 19 April 2021).
- Clapuyt, F.; Vanacker, V.; Van Oost, K. Reproducibility of UAV-based earth topography reconstructions based on Structure-from-Motion algorithms. Geomorphology 2016, 260, 4–15. [Google Scholar] [CrossRef]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Assessment of photogrammetric mapping accuracy based on variation ground control points number using unmanned aerial vehicle. Measurement 2017, 95, 221–227. [Google Scholar] [CrossRef]
- Oniga, V.-E.; Breaban, A.-I.; Statescu, F. Determining the Optimum Number of Ground Control Points for Obtaining High Precision Results Based on UAS Images. Proceedings 2018, 2, 5165. [Google Scholar] [CrossRef] [Green Version]
- Bolkas, D. Assessment of GCP Number and Separation Distance for Small UAS Surveys with and without GNSS-PPK Positioning. J. Surv. Eng. 2019, 145, 04019007. [Google Scholar] [CrossRef]
- Oniga, V.-E.; Breaban, A.-I.; Pfeifer, N.; Chirila, C. Determining the suitable number of ground control points for UAV images georeferencing by varying number and spatial distribution. Remote Sens. 2020, 12, 876. [Google Scholar] [CrossRef] [Green Version]
- Pix4Dmapper—Pix4D 2021. Available online: https://www.pix4d.com/product/pix4dmapper-photogrammetry-software (accessed on 19 April 2021).
- Kyriou, A.; Nikolakopoulos, K.; Koukouvelas, I. How image acquisition geometry of UAV campaigns affects the derived products and their accuracy in areas with complex geometry. ISPRS Int. J. Geo.-Inf. 2021, 10, 408. [Google Scholar] [CrossRef]
- FGCD—Federal Geographic Data Committee. Geospatial Positioning Accuracy Standards. FGDC-STD-007.3–1998. Part 3: National Standards for Spatial Data Accuracy (NSSDA); Federal Geographic Data Committee Secretariat c/o U.S. Geological Survey: Reston, VA, USA, 1998; pp. 1–25. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Sealy, G.W. The probable error of a mean. Biometrika 1908, 6, 1–25. [Google Scholar]
- Wilcoxon, F. Individual comparison by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- RStudio Team. RStudio: Integrated Development for R; RStudio Inc.: Boston, MA, USA, 2016. [Google Scholar]
- Harwin, S.; Lucieer, A.; Osborn, J. The impact of the calibration method on the accuracy of point clouds derived using unmanned aerial vehicle multi-view stereopsis. Remote Sens. 2015, 7, 11933–11953. [Google Scholar] [CrossRef] [Green Version]
- Przybilla, H.-J.; Bäumker, M. RTK and PPK: GNSS-Technologies for Direct Georeferencing of Uav Image Flights. In Proceedings of the FIG Working Week 2020, Amsterdam, The Netherlands, 10–14 May 2020; p. 52. [Google Scholar]










| Location | Area Surveyed (ha) | Georeferencing Method | Cameras Total/Aligned | Key Points per Images | Dense Cloud (nbr Points) | Orthomosaic, DSM Resolution (cm) |
|---|---|---|---|---|---|---|
| KEKEC | 3.4 | BBA_traditional | 135/135 | 65,326 | 45,662,559 (327.6/m3) | 2.4 |
| BBA_PPK | 45,754,260 (323.16/m3) | |||||
| KRNICA | 9.6 | BBA_traditional | 659/659 | 69,863 | 159,285,721 (836.51/m3) | 2.5 |
| BBA_PPK | 165,097,231 (756.25/m3) | |||||
| MANGART | 7.4 | BBA_traditional | 368/368 | 72,809 | 100,688,038 (1635.12/m3) | 2.2 |
| BBA_PPK | 106,209,704 (1707.94/m3) |
| Precision in m | X0 | Y0 | Z0 | |
|---|---|---|---|---|
| KEKEC | BBA_traditional | 0.012 | 0.009 | 0.019 |
| BBA_PPK | 0.006 | 0.012 | 0.013 | |
| KRNICA | BBA_traditional | 0.013 | 0.013 | 0.014 |
| BBA_PPK | 0.017 | 0.029 | 0.036 | |
| MANGART | BBA_traditional | 0.008 | 0.006 | 0.006 |
| BBA_PPK | 0.039 | 0.033 | 0.579 |
| Units in m | KEKEC | KRNICA | MANGART | |||
|---|---|---|---|---|---|---|
| BBA_Traditional | BBA_PPK | BBA_Traditional | BBA_PPK | BBA_Traditional | BBA_PPK | |
| diffX-MIN | −0.017 | −0.001 | −0.098 | −0.091 | −0.029 | −0.148 |
| diffX-MAX | 0.020 | 0.037 | 0.056 | 0.057 | 0.011 | −0.043 |
| diffX-MEAN | 0.004 | 0.017 | 0.001 | 0.013 | −0.004 | −0.098 |
| diffX-MEDIAN | 0.004 | 0.016 | 0.004 | 0.015 | −0.003 | −0.100 |
| diffX-SD | 0.008 | 0.009 | 0.026 | 0.029 | 0.008 | 0.028 |
| RMSEX | 0.009 | 0.019 | 0.026 | 0.032 | 0.009 | 0.102 |
| diffY-MIN | −0.028 | 0.000 | −0.033 | −0.041 | −0.024 | −0.171 |
| diffY-MAX | 0.016 | 0.044 | 0.091 | 0.100 | 0.013 | 0.001 |
| diffY-MEAN | −0.006 | 0.016 | 0.004 | 0.008 | −0.003 | −0.109 |
| diffY-MEDIAN | −0.006 | 0.015 | 0.001 | 0.002 | −0.002 | −0.118 |
| diffY-SD | 0.008 | 0.010 | 0.020 | 0.031 | 0.008 | 0.047 |
| RMSEY | 0.010 | 0.019 | 0.020 | 0.031 | 0.008 | 0.119 |
| diffZ-MIN | −0.010 | 0.023 | −0.022 | −0.102 | −0.014 | 0.102 |
| diffZ-MAX | 0.037 | 0.069 | 0.038 | −0.004 | 0.015 | 0.431 |
| diffZ-MEAN | 0.009 | 0.049 | 0.004 | −0.042 | 0.002 | 0.245 |
| diffZ-MEDIAN | 0.009 | 0.048 | 0.001 | −0.040 | 0.003 | 0.232 |
| diffZ-SD | 0.010 | 0.010 | 0.014 | 0.023 | 0.007 | 0.092 |
| RMSEz | 0.014 | 0.050 | 0.015 | 0.048 | 0.007 | 0.261 |
| RMSEXYZ | 0.019 | 0.056 | 0.036 | 0.066 | 0.014 | 0.305 |
| LEGEND | ||||||
| diff(X/Y/Z)-MIN | the minimum value of the differences in X/Y/Z | |||||
| diff(X/Y/Z)-MAX | the maximum value of the differences in X/Y/Z | |||||
| diff(X/Y/Z)-MEAN | the mean value of the differences in X/Y/Z | |||||
| diff(X/Y/Z)-MEDIAN | the median value of the differences in X/Y/Z | |||||
| diff(X/Y/Z)-SD | the standard deviation of the differences in X/Y/Z | |||||
| RMSE(X/Y/Z) | root mean square error of X/Y/Z | |||||
| Units in m. | KEKEC | KRNICA | MANGART | |||
|---|---|---|---|---|---|---|
| Orthomosaic_Traditional | Orthomosaic_PPK | Orthomosaic_Traditional | Orthomosaic_PPK | Orthomosaic_Traditional | Orthomosaic_PPK | |
| diffX-MIN | −0.007 | 0.008 | −0.104 | −0.079 | −0.011 | −0.139 |
| diffX-MAX | 0.045 | 0.061 | 0.046 | 0.052 | 0.037 | −0.026 |
| diffX-MEAN | 0.018 | 0.032 | 0.000 | 0.014 | 0.011 | −0.089 |
| diffX-MEDIAN | 0.018 | 0.031 | 0.003 | 0.017 | 0.012 | −0.088 |
| diffX-SD | 0.012 | 0.012 | 0.027 | 0.028 | 0.012 | 0.026 |
| RMSEX | 0.021 | 0.034 | 0.026 | 0.031 | 0.016 | 0.093 |
| diffY-MIN | −0.036 | −0.013 | −0.056 | −0.041 | −0.044 | −0.181 |
| diffY-MAX | 0.011 | 0.039 | 0.078 | 0.106 | 0.016 | −0.016 |
| diffY-MEAN | −0.017 | 0.013 | −0.012 | 0.006 | −0.005 | −0.119 |
| diffY-MEDIAN | −0.016 | 0.011 | −0.013 | 0.002 | −0.002 | −0.133 |
| diffY-SD | 0.011 | 0.012 | 0.022 | 0.029 | 0.012 | 0.045 |
| RMSEY | 0.020 | 0.017 | 0.025 | 0.030 | 0.013 | 0.127 |
| RMSEXY | 0.029 | 0.039 | 0.036 | 0.043 | 0.020 | 0.157 |
| LEGEND | ||||||
| diff(X/Y)-MIN | the minimum value of the differences in X/Y | |||||
| diff(X/Y)-MAX | the maximum value of the differences in X/Y | |||||
| diff(X/Y)-MEAN | the mean value of the differences in X/Y | |||||
| diff(X/Y)-MEDIAN | the median value of the differences in X/Y | |||||
| diff(X/Y)-SD | the standard deviation of the differences in X/Y | |||||
| RMSE(X/Y) | root mean square error of X/Y | |||||
| Units in m | KEKEC | KRNICA | MANGART | |||
|---|---|---|---|---|---|---|
| DSM_Traditional | DSM_PPK | DSM_Traditional | DSM_PPK | DSM_Traditional | DSM_PPK | |
| diffZ-MIN | −0.051 | −0.002 | −0.079 | −0.129 | −0.053 | 0.081 |
| diffZ-MAX | 0.122 | 0.184 | 0.165 | 0.245 | 0.042 | 0.453 |
| diffZ-MEAN | 0.010 | 0.053 | 0.026 | −0.002 | −0.022 | 0.244 |
| diffZ-MEDIAN | 0.013 | 0.048 | 0.019 | −0.005 | −0.022 | 0.237 |
| diffZ-SD | 0.037 | 0.037 | 0.055 | 0.072 | 0.021 | 0.093 |
| RMSEZ | 0.038 | 0.065 | 0.060 | 0.072 | 0.030 | 0.261 |
| LEGEND | ||||||
| diffZ-MIN | the minimum value of the differences in Z | |||||
| diffZ-MAX | the maximum value of the differences in Z | |||||
| diffZ-MEAN | the mean value of the differences in Z | |||||
| diffZ-MEDIAN | the median value of the differences in Z | |||||
| diffZ-SD | the standard deviation of the differences in Z | |||||
| RMSEZ | root mean square error of Z | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Žabota, B.; Kobal, M. Accuracy Assessment of UAV-Photogrammetric-Derived Products Using PPK and GCPs in Challenging Terrains: In Search of Optimized Rockfall Mapping. Remote Sens. 2021, 13, 3812. https://doi.org/10.3390/rs13193812
Žabota B, Kobal M. Accuracy Assessment of UAV-Photogrammetric-Derived Products Using PPK and GCPs in Challenging Terrains: In Search of Optimized Rockfall Mapping. Remote Sensing. 2021; 13(19):3812. https://doi.org/10.3390/rs13193812
Chicago/Turabian StyleŽabota, Barbara, and Milan Kobal. 2021. "Accuracy Assessment of UAV-Photogrammetric-Derived Products Using PPK and GCPs in Challenging Terrains: In Search of Optimized Rockfall Mapping" Remote Sensing 13, no. 19: 3812. https://doi.org/10.3390/rs13193812
APA StyleŽabota, B., & Kobal, M. (2021). Accuracy Assessment of UAV-Photogrammetric-Derived Products Using PPK and GCPs in Challenging Terrains: In Search of Optimized Rockfall Mapping. Remote Sensing, 13(19), 3812. https://doi.org/10.3390/rs13193812