Airborne SAR Autofocus Based on Blurry Imagery Classification
Abstract
:1. Introduction
2. Problem Formulation and Motivation
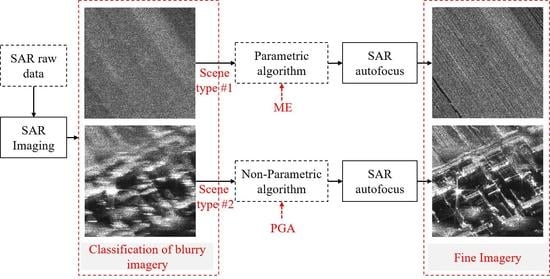
3. Autofocus Approach Based on Blurry Imagery Classification
3.1. Imaging Processing
3.2. Blurry Imagery Classification
3.3. Autofocus Processing
4. Processing Results of Real Data
4.1. Classification Verification
4.2. Autofocus Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Lan, Y.; Yuan, Z.; Xu, J.; Lee, H. Phase Unwrapping in InSAR: A Review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 40–58. [Google Scholar] [CrossRef]
- Xu, G.; Gao, Y.; Li, J.; Xing, M. InSAR Phase Denoising: A Review of Current Technologies and Future Directions. IEEE Geosci. Remote Sens. Mag. 2020, 8, 64–82. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Zhang, J.; Jin, Y.; Yu, H.; Liang, B.; Yang, D. Real-Time Processing of Spaceborne SAR Data with Nonlinear Trajectory Based on Variable PRF. IEEE Trans. Geosci. Remote. Sens. 2021, 1–12. [Google Scholar] [CrossRef]
- Xiong, Y.; Liang, B.; Yu, H.; Chen, J.; Jin, Y.; Xing, M. Processing of Bistatic SAR Data With Nonlinear Trajectory Using a Controlled-SVD Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5750–5759. [Google Scholar] [CrossRef]
- Chen, X.; Sun, G.C.; Xing, M.; Li, B.; Yang, J.; Bao, Z. Ground Cartesian Back-Projection Algorithm for High Squint Diving TOPS SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5812–5827. [Google Scholar] [CrossRef]
- Yi, T.; He, Z.; He, F.; Dong, Z.; Wu, M.; Song, Y. A Compensation Method for Airborne SAR with Varying Accelerated Motion Error. Remote Sens. 2018, 10, 1124. [Google Scholar] [CrossRef] [Green Version]
- Kirk, J.C. Motion Compensation for Synthetic Aperture Radar. IEEE Trans. Aerosp. Electron. Syst. 1975, AES-11, 338–348. [Google Scholar] [CrossRef]
- Moreira, J.R. A New Method Of Aircraft Motion Error Extraction From Radar Raw Data For Real Time Motion Compensation. IEEE Trans. Geosci. Remote Sens. 1990, 28, 620–626. [Google Scholar] [CrossRef]
- Fornaro, G. Trajectory deviations in airborne SAR: Analysis and compensation. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 997–1009. [Google Scholar] [CrossRef]
- Lu, Q.; Huang, P.; Gao, Y.; Liu, X. Precise frequency division algorithm for residual aperture-variant motion compensation in synthetic aperture radar. Electron. Lett. 2019, 55, 51–53. [Google Scholar] [CrossRef]
- Moreira, A.; Huang, Y. Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1029–1040. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Sun, G.; Li, Z. A 2-D Space-Variant Motion Estimation and Compensation Method for Ultrahigh-Resolution Airborne Stepped-Frequency SAR With Long Integration Time. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6390–6401. [Google Scholar] [CrossRef]
- Chen, J.; Liang, B.; Yang, D.; Zhao, D.; Xing, M.; Sun, G. Two-Step Accuracy Improvement of Motion Compensation for Airborne SAR With Ultrahigh Resolution and Wide Swath. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7148–7160. [Google Scholar] [CrossRef]
- Xing, M.; Jiang, X.; Wu, R.; Zhou, F.; Bao, Z. Motion Compensation for UAV SAR Based on Raw Radar Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2870–2883. [Google Scholar] [CrossRef]
- Zhang, L.; Qiao, Z.; Xing, M.; Yang, L.; Bao, Z. A Robust Motion Compensation Approach for UAV SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3202–3218. [Google Scholar] [CrossRef]
- Li, N.; Niu, S.; Guo, Z.; Liu, Y.; Chen, J. Raw Data-Based Motion Compensation for High-Resolution Sliding Spotlight Synthetic Aperture Radar. Sensors 2018, 18, 842. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Zhang, M.; Huang, Y.; Zhang, L.; Wang, F. Robust Two-Dimensional Spatial-Variant Map-Drift Algorithm for UAV SAR Autofocusing. Remote Sens. 2019, 11, 340. [Google Scholar] [CrossRef] [Green Version]
- Berizzi, F.; Martorella, M.; Cacciamano, A.; Capria, A. A Contrast-Based Algorithm For Synthetic Range-Profile Motion Compensation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3053–3062. [Google Scholar] [CrossRef]
- Xiong, T.; Xing, M.; Wang, Y.; Wang, S.; Sheng, J.; Guo, L. Minimum-Entropy-Based Autofocus Algorithm for SAR Data Using Chebyshev Approximation and Method of Series Reversion, and Its Implementation in a Data Processor. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1719–1728. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, S.; Zhao, L.; Xing, M. Coherent Auto-Calibration of APE and NsRCM under Fast Back-Projection Image Formation for Airborne SAR Imaging in Highly-Squint Angle. Remote Sens. 2018, 10, 321. [Google Scholar] [CrossRef] [Green Version]
- Bao, M.; Zhou, S.; Xing, M. Processing Missile-Borne SAR Data by Using Cartesian Factorized Back Projection Algorithm Integrated with Data-Driven Motion Compensation. Remote Sens. 2021, 13, 1462. [Google Scholar] [CrossRef]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; Yeo, T.S.; Bao, Z. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2487–2494. [Google Scholar] [CrossRef] [Green Version]
- Zhu, D.; Jiang, R.; Mao, X.; Zhu, Z. Multi-Subaperture PGA for SAR Autofocusing. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 468–488. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, W.; Liu, Y.; Wang, R.; Shi, C. Sharpness-Based Autofocusing for Stripmap SAR Using an Adaptive-Order Polynomial Model. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1086–1090. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Wei, S.; Liang, J.; Wang, M.; Zeng, X.; Shi, J.; Zhang, X. CIST: An Improved ISAR Imaging Method Using Convolution Neural Network. Remote Sens. 2020, 12, 2641. [Google Scholar] [CrossRef]
- Hu, C.; Wang, L.; Li, Z.; Zhu, D. Inverse Synthetic Aperture Radar Imaging Using a Fully Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1203–1207. [Google Scholar] [CrossRef]
- Li, R.; Zhang, S.; Zhang, C.; Liu, Y.; Li, X. Deep Learning Approach for Sparse Aperture ISAR Imaging and Autofocusing Based on Complex-Valued ADMM-Net. IEEE Sens. J. 2021, 21, 3437–3451. [Google Scholar] [CrossRef]
- Gao, J.; Deng, B.; Qin, Y.; Wang, H.; Li, X. Enhanced Radar Imaging Using a Complex-Valued Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2019, 16, 35–39. [Google Scholar] [CrossRef] [Green Version]
- Cumming, I.G.; Wong, F.H.C. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Mao, X.; Zhu, D. Two-dimensional Autofocus for Spotlight SAR Polar Format Imagery. IEEE Trans. Comput. Imaging 2016, 2, 524–539. [Google Scholar] [CrossRef] [Green Version]
- Mao, X.; He, X.; Li, D. Knowledge-Aided 2-D Autofocus for Spotlight SAR Range Migration Algorithm Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5458–5470. [Google Scholar] [CrossRef]
- Jakowatz, C.V.; Wahl, D.E. Eigenvector method for maximum-likelihood estimation of phase errors in synthetic-aperture-radar imagery. JOSA A 1993, 10, 2539–2546. [Google Scholar] [CrossRef]







| Autofocus Methods | Applicable Conditions | |
|---|---|---|
| Non-parametric methods | DSA | Corner reflectors |
| PGA | Dominant points | |
| Parametric methods | MD | Low-frequency motion error |
| CO/ME | Non-real-time processing |
| SAR Imagery | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
|---|---|---|---|---|---|---|---|---|---|---|
| Actual Type | #2 | #1 | #1 | #2 | #1 | #2 | #2 | #1 | #2 | #1 |
| Downsampling processing | #1 | #1 | #1 | #1 | #1 | #1 | #2 | #1 | #2 | #1 |
| Ratio of type #1 | 91/144 | 144/144 | 143/144 | 110/144 | 7/7 | 3/7 | 1/7 | 139/144 | 0/7 | 33/36 |
| Ratio of type #2 | 53/144 | 0/144 | 1/144 | 34/144 | 0/7 | 4/7 | 6/7 | 5/144 | 7/7 | 3/36 |
| Type by our method (98%) | #2 | #1 | #1 | #2 | #1 | #2 | #2 | #2 | #2 | #2 |
| Type by our method (96%) | #2 | #1 | #1 | #2 | #1 | #2 | #2 | #1 | #2 | #2 |
| Type by our method (94%) | #2 | #1 | #1 | #2 | #1 | #2 | #2 | #1 | #2 | #2 |
| SAR Imagery | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
|---|---|---|---|---|---|---|---|---|---|---|
| Actual Type | #2 | #1 | #1 | #2 | #1 | #2 | #2 | #1 | #2 | #1 |
| Downsampling processing | #1 | #1 | #1 | #1 | #1 | #1 | #2 | #1 | #2 | #1 |
| Ratio of type #1 | 95/144 | 143/144 | 143/144 | 109/144 | 7/7 | 3/7 | 2/7 | 139/144 | 2/7 | 34/36 |
| Ratio of type #2 | 49/144 | 1/144 | 1/144 | 35/144 | 0/7 | 4/7 | 5/7 | 5/144 | 5/7 | 2/36 |
| Type by our method (98%) | #2 | #1 | #1 | #2 | #1 | #2 | #2 | #2 | #2 | #2 |
| Type by our method (96%) | #2 | #1 | #1 | #2 | #1 | #2 | #2 | #1 | #2 | #2 |
| Type by our method (94%) | #2 | #1 | #1 | #2 | #1 | #2 | #2 | #1 | #2 | #1 |
| Entropy Value | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SAR imagery | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
| No autofocus | 12.85 | 13.44 | 13.46 | 13.06 | 13.04 | 12.35 | 12.04 | 13.46 | 12.28 | 12.90 |
| PGA autofocus | 12.70 | 13.46 | 13.46 | 12.97 | 13.06 | 12.27 | 11.98 | 13.46 | 12.05 | 12.91 |
| ME autofocus | 12.72 | 13.33 | 13.35 | 12.97 | 13.01 | 12.29 | 11.99 | 13.40 | 12.14 | 12.86 |
| Proposed autofocus | 12.70 | 13.33 | 13.35 | 12.97 | 13.01 | 12.27 | 11.98 | 13.40 | 12.05 | 12.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Yu, H.; Xu, G.; Zhang, J.; Liang, B.; Yang, D. Airborne SAR Autofocus Based on Blurry Imagery Classification. Remote Sens. 2021, 13, 3872. https://doi.org/10.3390/rs13193872
Chen J, Yu H, Xu G, Zhang J, Liang B, Yang D. Airborne SAR Autofocus Based on Blurry Imagery Classification. Remote Sensing. 2021; 13(19):3872. https://doi.org/10.3390/rs13193872
Chicago/Turabian StyleChen, Jianlai, Hanwen Yu, Gang Xu, Junchao Zhang, Buge Liang, and Degui Yang. 2021. "Airborne SAR Autofocus Based on Blurry Imagery Classification" Remote Sensing 13, no. 19: 3872. https://doi.org/10.3390/rs13193872
APA StyleChen, J., Yu, H., Xu, G., Zhang, J., Liang, B., & Yang, D. (2021). Airborne SAR Autofocus Based on Blurry Imagery Classification. Remote Sensing, 13(19), 3872. https://doi.org/10.3390/rs13193872