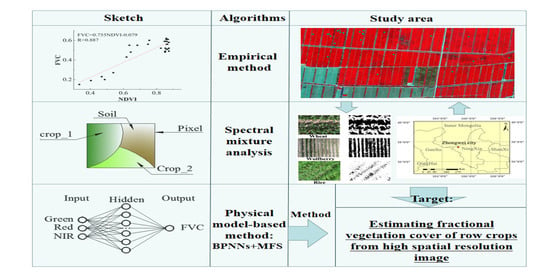
Estimating Fractional Vegetation Cover of Row Crops from High Spatial Resolution Image
Abstract
:1. Introduction
2. Methods
2.1. Empirical Method
2.2. Spectral Mixture Analysis
2.2.1. Unconstrained SMA
2.2.2. Constrained SMA
2.2.3. Number of Endmembers
2.3. Physical Model-Based Method
2.3.1. Generating the Learning Dataset
2.3.2. Training Network
2.3.3. Retrieving FVC
3. Experiment and Data Preparation
3.1. Field Measurement Data
3.1.1. Endmember Spectrum and Normalized Vegetation Index
3.1.2. Fractional Vegetation Cover
3.2. Remote Sensing Data, Preprocessing, and Implementation of Estimated Algorithm of FVC
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Mu, X.; Song, W.; Gao, Z.; Mcvicar, T.R.; Donohue, R.J.; Yan, G. Fractional vegetation cover estimation by using multi-angle vegetation index. Remote Sens. Environ. 2018, 216, 44–56. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [Green Version]
- Mhango, J.K.; Harris, E.W.; Green, R.; Monaghan, J.M. Mapping Potato Plant Density Variation Using Aerial Imagery and Deep Learning Techniques for Precision Agriculture. Remote Sens. 2021, 13, 2705. [Google Scholar] [CrossRef]
- Mulla, D.J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Guillen-Climent, M.; Zarco-Tejada, P.; Berni, J.; North, P.; Villalobos, F. Mapping radiation interception in row-structured orchards using 3D simulation and high-resolution airborne imagery acquired from a UAV. Precis. Agric. 2012, 13, 473–500. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Wang, T.; Lu, L. A Refined Four-Stream Radiative Transfer Model for Row-Planted Crops. Remote Sens. 2020, 12, 1290. [Google Scholar] [CrossRef] [Green Version]
- Jia, K.; Liang, S.; Gu, X.; Baret, F.; Wei, X.; Wang, X.; Yao, Y.; Yang, L.; Li, Y. Fractional vegetation cover estimation algorithm for Chinese GF-1 wide field view data. Remote Sens. Environ. 2016, 177, 184–191. [Google Scholar] [CrossRef]
- Yan, G.J.; Mu, X.; Liu, Y. Chapter 12-Fractional vegetation cover. In Advanced Remote Sensing, 2nd ed.; Liang, S., Wang, J., Eds.; Academic Press: Cambridge, UK, 2020; pp. 477–510. [Google Scholar] [CrossRef]
- Yang, L.; Jia, K.; Liang, S.; Liu, J.; Wang, X. Comparison of Four Machine Learning Methods for Generating the GLASS Fractional Vegetation Cover Product from MODIS Data. Remote Sens. 2016, 8, 682. [Google Scholar] [CrossRef] [Green Version]
- Jiapaer, G.; Chen, X.; Bao, A. A comparison of methods for estimating fractional vegetation cover in arid regions. Agric. For. Meteorol. 2011, 151, 1698–1710. [Google Scholar] [CrossRef]
- Ormsby, J.P.; Choudhury, B.J.; Owe, M. Vegetation spatial variability and its effect on vegetation indices. Int. J. Remote Sens. 1987, 8, 6. [Google Scholar] [CrossRef]
- Li, F.; Kustas, W.P.; Prueger, J.H.; Neale, C.M.U.; Jackson, T.J. Utility of Remote Sensing–Based Two-Source Energy Balance Model under Low- and High-Vegetation Cover Conditions. J. Hydrometeorol. 2005, 6, 878–891. [Google Scholar] [CrossRef]
- Chen, F.; Ke, W.; Tang, T.F. Spectral Unmixing Using a Sparse Multiple-Endmember Spectral Mixture Model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5846–5861. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Deardorff, J.W. Efficient Prediction of Ground Surface Temperature and Moisture With Inclusion of a Layer of Vegetation. J. Geophys. Res. Ocean. 1978, 83, 1889–1903. [Google Scholar] [CrossRef] [Green Version]
- Song, W.; Mu, X.; Ruan, G.; Gao, Z.; Li, L.; Yan, G. Estimating fractional vegetation cover and the vegetation index of bare soil and highly dense vegetation with a physically based method. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 168–176. [Google Scholar] [CrossRef]
- Heinz, D.C.; Chang, C. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 39, 529–545. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Qihao, W. Spectral Mixture Analysis of the Urban Landscape in Indianapolis with Landsat ETM+ Imagery. Photogramm. Eng. Remote Sens. 2004, 70, 1053–1062. [Google Scholar] [CrossRef] [Green Version]
- Okin, G.S. Relative spectral mixture analysis—A multitemporal index of total vegetation cover. Remote Sens. Environ. 2007, 106, 467–479. [Google Scholar] [CrossRef]
- García-Haro, F.J.; Sommer, S.; Kemper, T. A new tool for variable multiple endmember spectral mixture analysis (VMESMA). Int. J. Remote Sens. 2005, 26, 2135–2162. [Google Scholar] [CrossRef] [Green Version]
- Xiao, J.F.; Moody, A. A comparison of methods for estimating fractional green vegetation cover within a desert-to-upland transition zone in central New Mexico, USA. Remote Sens. Environ. 2005, 98, 237–250. [Google Scholar] [CrossRef]
- Wu, D.; Wu, H.; Zhao, X.; Zhou, T.; Tang, B.; Zhao, W.; Jia, K. Evaluation of Spatiotemporal Variations of Global Fractional Vegetation Cover Based on GIMMS NDVI Data from 1982 to 2011. Remote Sens. 2014, 6, 4217–4239. [Google Scholar] [CrossRef] [Green Version]
- Zhan, Y.; Meng, Q.; Wang, C.; Li, J.; Li, D. Fractional vegetation cover estimation over large regions using GF-1 satellite data. Proc. Spie Int. Soc. Opt. Eng. 2014, 9260. [Google Scholar]
- Jia, K.; Liang, S.; Liu, S.; Li, Y.; Xiao, Z.; Yao, Y.; Jiang, B.; Zhao, X.; Wang, X.; Xu, S.; et al. Global Land Surface Fractional Vegetation Cover Estimation Using General Regression Neural Networks From MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4787–4796. [Google Scholar] [CrossRef]
- Jain, R.; Shetty, A.; Oak, S.; Wajekar, A. Global mapping of vegetation parameters from POLDER multiangular measurements for studies of surface-atmosphere interactions: A pragmatic method and its validation. J. Geophys. Res. Atmos. 2002, 107, ACL6-1–ACL6-14. [Google Scholar]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmara, H.; Pacholcyzk, P.; Smets, B. GEOV1: LAI and FAPAR essential climate variables and FCOVER global time series capitalizing over existing products. Part1: Principles of development and production. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Jia, K.; Liang, S.; Wei, X.; Li, Q.; Du, X.; Jiang, B.; Yao, Y.; Zhao, X.; Li, Y. Fractional Forest Cover Changes in Northeast China From 1982 to 2011 and Its Relationship With Climatic Variations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 775–783. [Google Scholar] [CrossRef]
- Mu, X.; Huang, S.; Yan, G.; Song, W.; Ruan, G. Validating GEOV1 Fractional Vegetation Cover Derived From Coarse-Resolution Remote Sensing Images Over Croplands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 439–446. [Google Scholar] [CrossRef]
- Hurcom, S.J.; Harrison, A.R. The NDVI and spectral decomposition for semi-arid vegetation abundance estimation. Int. J. Remote Sens. 1998, 19, 3109–3125. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef] [Green Version]
- Peterson, S.H.; Stow, D.A. Using multiple image endmember spectral mixture analysis to study chaparral regrowth in southern California. Int. J. Remote Sens. 2003, 24, 4481–4504. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef] [Green Version]
- Elmore, A.J.; Mustard, J.F.; Manning, S.J.; Lobell, D.B. Quantifying Vegetation Change in Semiarid Environments: Precision and Accuracy of Spectral Mixture Analysis and the Normalized Difference Vegetation Index. Remote Sens. Environ. 2000, 73, 87–102. [Google Scholar] [CrossRef]
- Cheng, I.C.; Xiao-Li, Z.; Althouse, M.L.G.; Jeng Jong, P. Least squares subspace projection approach to mixed pixel classification for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 898–912. [Google Scholar] [CrossRef] [Green Version]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; Maire, G.L.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Hosgood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf Optical Properties EXperiment 93 (LOPEX93); Office for Official Publications of the European Communities: Luxembourg, 1994. [Google Scholar]
- Matthew, M.W.; Adler-Golden, S.M.; Berk, A.; Richtsmeier, S.C.; Hoke, M.P. Status of Atmospheric Correction using a MODTRAN4-Based Algorithm. Proc. SPIE Int. Soc. Opt. Eng. 2000, 4049, 11. [Google Scholar]
- Xiao, Z.; Wang, T.; Liang, S.; Sun, R. Estimating the Fractional Vegetation Cover from GLASS Leaf Area Index Product. Remote Sens. 2016, 8, 337. [Google Scholar] [CrossRef] [Green Version]
- Mu, X.H.; Liu, Q.H.; Ruan, G.Y.; Zhao, J.; Zhong, B.; Wu, S.; Peng, J.J. 1 km/5 day fractional vegetation cover dataset over China-ASEAN. J. Glob. Chang. Data Discov. 2017, 1, 45–51. [Google Scholar]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION : Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Weiss, M.; Baret, F.; Garrigues, S.; Lacaze, R. LAI and fAPAR CYCLOPES global products derived from VEGETATION. Part 2: Validation and comparison with MODIS collection 4 products. Remote Sens. Environ. 2007, 110, 317–331. [Google Scholar] [CrossRef]
- Lacaze, R.; Richaume, P.; Hautecoeur, O.; Lanlanne, T.; Quesney, A.; MAIGNAN, F.; BICHeron, P.; Leroy, M.; Bréon, F.M. Advanced algorithms of the ADEOS-2/POLDER-2 land surface process line: Application to the ADEOS-1/POLDER-1 data. IEEE Int. Geosci. Remote Sens. Symp. 2003, 5, 3259–3262. [Google Scholar]
- Wang, B.; Jia, K.; Liang, S.; Xie, X.; Wei, X.; Zhao, X.; Yao, Y.; Zhang, X. Assessment of Sentinel-2 MSI Spectral Band Reflectances for Estimating Fractional Vegetation Cover. Remote Sens. 2018, 10, 1927. [Google Scholar] [CrossRef] [Green Version]
- Guerschman, J.P.; Hill, M.J.; Renzullo, L.J.; Barrett, D.J.; Marks, A.S.; Botha, E.J. Estimating fractional cover of photosynthetic vegetation, non-photosynthetic vegetation and bare soil in the Australian tropical savanna region upscaling the EO-1 Hyperion and MODIS sensors. Remote Sens. Environ. 2009, 113, 928–945. [Google Scholar] [CrossRef]






| MFS Model | PROSAIL Model | ||||||
|---|---|---|---|---|---|---|---|
| Parameter | Unit | Value Range | Step | Parameter | Unit | Value Range | Step |
| Cab | μg·cm−2 | 30–60 | 10 | Cab | μg·cm−2 | 30–60 | 10 |
| Car | μg·cm−2 | 4–14 | 2 | Car | μg·cm−2 | 4–14 | 2 |
| N | - | 1.2–1.8 | 0.2 | CW | cm | 0.005–0.0015 | 0.005 |
| θl | ° | 30–70 | 10 | Cm | g·cm−2 | 0.003–0.005 | 0.001 |
| L | m2·m−2 | 0–6 | 0.5 | N | - | 1.2–1.8 | 0.2 |
| θs | ° | 20–45 | 5 | θl | ° | 30–70 | 10 |
| A1 | cm | 0–20 | 10 | LAI | m2·m−2 | 0–6 | 0.5 |
| A2 | cm | 0–20 | 10 | θs | ° | 20–45 | 5 |
| Number of Network Cycles (P) | Number of Nodes in the Layers | Learning Efficiency (α) | Damping Coefficient (β) | |||
|---|---|---|---|---|---|---|
| Input | Hidden | Output | ||||
| value | 414 | 3 | 6 (MFS + BPNN) | 1 | 0.01 | 0.1 |
| specific contents | 545 nm (r) 660 nm (r) 782 nm (r) | 14 (PROSAIL_BPNNs) | FVC | |||
| Satellite Height | Band | Acquisition Date and Time | Spatial Resolution |
|---|---|---|---|
| 617 km | Coastal (400 nm–450 nm) | 2 July, 12:15:34 (Beijing time) | 2 m |
| Blue (450 nm–510 nm) | |||
| Green (510 nm–580 nm) | |||
| Yellow (585 nm–625 nm) | |||
| Red (630 nm–690 nm) | |||
| Red–Edge(705 nm–74 nm) | |||
| NIR–1 (770 nm–895 nm) | |||
| NIR–2 (860 nm–1040 nm) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Lu, L.; Ding, J.; Zhang, F.; He, B. Estimating Fractional Vegetation Cover of Row Crops from High Spatial Resolution Image. Remote Sens. 2021, 13, 3874. https://doi.org/10.3390/rs13193874
Ma X, Lu L, Ding J, Zhang F, He B. Estimating Fractional Vegetation Cover of Row Crops from High Spatial Resolution Image. Remote Sensing. 2021; 13(19):3874. https://doi.org/10.3390/rs13193874
Chicago/Turabian StyleMa, Xu, Lei Lu, Jianli Ding, Fei Zhang, and Baozhong He. 2021. "Estimating Fractional Vegetation Cover of Row Crops from High Spatial Resolution Image" Remote Sensing 13, no. 19: 3874. https://doi.org/10.3390/rs13193874
APA StyleMa, X., Lu, L., Ding, J., Zhang, F., & He, B. (2021). Estimating Fractional Vegetation Cover of Row Crops from High Spatial Resolution Image. Remote Sensing, 13(19), 3874. https://doi.org/10.3390/rs13193874