Field-Based High-Quality Emissivity Spectra Measurement Using a Fourier Transform Thermal Infrared Hyperspectral Imager
Abstract
:1. Introduction
- (1)
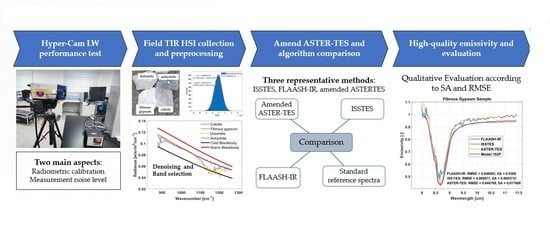
- A practical data measurement and processing framework was specifically proposed for the Hyper-Cam LW sensor that includes four aspects: the performance validation of the Hyper-Cam LW sensor, a field-based acquisition procedure for TIR hyperspectral imagery, data preprocessing to improve the original data quality, and appropriate TES algorithm selection via the comparison of three representative methods.
- (2)
- Data improvement was performed through band selection, imagery denoising, and environmental correction. In addition, according to the analysis of the noise distribution type and magnitude, a spatial denoising method based on Gaussian template convolution was adopted to preserve the atmospheric radiance features in the spectrum.
- (3)
- Three widely used TES algorithms were investigated and compared using Hyper-Cam LW field-measured TIR hyperspectral imagery, and the optimal TES method was selected to determine the final high-quality emissivity spectra that were quantitatively evaluated using the standard spectra measured by the Model 102F spectrometer.
2. Instrument Testing and Data Acquisition
2.1. Instrumentation and Configuration
2.2. Instrument Performance Testing
2.2.1. Radiometric Calibration and Stability Testing
2.2.2. Measurement Noise Level Estimation
2.3. Field Data Acquisition
2.3.1. Instrument and Sample Preparation
2.3.2. Imagery Calibration and Measurement
2.3.3. Environmental Radiation Measurement
3. Data Preprocessing and Quality Improvement
3.1. TIR Hyperspectral Imagery Denoising
3.2. Environmental Radiance Correction and Atmospheric Effect Analysis
3.3. Band Selection
4. Temperature and Emissivity Separation Algorithms
4.1. Thermal Infrared Radiative Transfer Model for Field Measurement
4.2. The Temperature and Emissivity Separation Methods for Emissivity Retrieval
4.2.1. The ISSTES Method
4.2.2. The FLAASH-IR Method
4.2.3. The Modified ASTER-TES Method
4.3. Evaluation Indicator
5. Results and Discussion
5.1. Qualitative Evaluation of the Temperature and Emissivity Maps
5.2. Quantitative Accuracy Evaluation of the Retrieved Emissivity Spectra
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manolakis, D.; Pieper, M.; Truslow, E.; Lockwood, R.; Weisner, A.; Jacobson, J.; Cooley, T. Longwave infrared hyperspectral imaging: Principles, progress, and challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 72–100. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.-H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Ni, L.; Xu, H.G.; Zhou, X.M. Mineral Identification and Mapping by Synthesis of Hyperspectral VNIR/SWIR and Multispectral TIR Remotely Sensed Data with Different Classifiers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3155–3163. [Google Scholar] [CrossRef]
- Puckrin, E.; Turcotte, C.S.; Lahaie, P.; Dubé, D.; Farley, V.; Lagueux, P.; Marcotte, F.; Chamberland, M. Airborne infrared-hyperspectral mapping for detection of gaseous and solid targets. SPIE Def. Secur. Sens. 2010, 7665, 10. [Google Scholar]
- Zhu, X.; Cao, L.; Wang, S.; Gao, L.; Zhong, Y.J.R.S. Anomaly Detection in Airborne Fourier Transform Thermal Infrared Spectrometer Images Based on Emissivity and a Segmented Low-Rank Prior. Remote Sens. 2021, 13, 754. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Liu, H.; Wu, K.; Xu, H.; Xu, Y.J.R.S. Lithology Classification Using TASI Thermal Infrared Hyperspectral Data with Convolutional Neural Networks. Remote Sens. 2021, 13, 3117. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Grigsby, S.P.; Hulley, G.C.; Roberts, D.A.; Scheele, C.; Ustin, S.L.; Alsina, M.M. Improved surface temperature estimates with MASTER/AVIRIS sensor fusion. Remote Sens. Environ. 2015, 167, 53–63. [Google Scholar] [CrossRef] [Green Version]
- Malakar, N.K.; Hulley, G.C. A water vapor scaling model for improved land surface temperature and emissivity separation of MODIS thermal infrared data. Remote Sens. Environ. 2016, 182, 252–264. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Ye, X.; Ren, H.; Liang, Y.; Zhu, J.; Guo, J.; Nie, J.; Zeng, H.; Zhao, Y.; Qian, Y. Cross-calibration of Chinese Gaofen-5 thermal infrared images and its improvement on land surface temperature retrieval. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102357. [Google Scholar] [CrossRef]
- Yang, J.; Duan, S.-B.; Zhang, X.; Wu, P.; Huang, C.; Leng, P.; Gao, M.J.R.S. Evaluation of Seven Atmospheric Profiles from Reanalysis and Satellite-Derived Products: Implication for Single-Channel Land Surface Temperature Retrieval. Remote Sens. 2020, 12, 791. [Google Scholar] [CrossRef] [Green Version]
- Wan, Z.; Li, Z.-L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar]
- Zhao, E.; Gao, C.; Yao, Y. New land surface temperature retrieval algorithm for heavy aerosol loading during nighttime from Gaofen-5 satellite data. Opt. Express 2020, 28, 2583–2599. [Google Scholar] [CrossRef]
- Yuan, L.; He, Z.; Lv, G.; Wang, Y.; Li, C.; Wang, J. Optical design, laboratory test, and calibration of airborne long wave infrared imaging spectrometer. Opt. Express 2017, 25, 22440–22454. [Google Scholar] [CrossRef]
- Hackwell, J.A.; Warren, D.W.; Bongiovi, R.P.; Hansel, S.J.; Hayhurst, T.L.; Mabry, D.J.; Sivjee, M.G.; Skinner, J.W. LWIR/MWIR imaging hyperspectral sensor for airborne and ground-based remote sensing. In Proceedings of the Imaging Spectrometry II, Denver, CO, USA., 4–9 August 1996; pp. 102–107. [Google Scholar]
- Wang, H.; Xiao, Q.; Li, H.; Zhong, B. Temperature and emissivity separation algorithm for TASI airborne thermal hyperspectral data. In Proceedings of the 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11 September 2011; pp. 1075–1078. [Google Scholar]
- Montembeault, Y.; Lagueux, P.; Farley, V.; Villemaire, A.; Gross, K.C. Hyper-Cam: Hyperspectral IR imaging applications in defence innovative research. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Yang, H.; Lifu, Z.; Yingqian, G.; Hu, S.; Li, X.; Genzhong, Z.; Qingxi, T. Temperature and Emissivity Separation from Thermal Airborne Hyperspectral Imager (TASI) Data. Photogramm. Eng. Remote Sens. 2013, 79, 1099–1107. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Wu, H.; Jiang, X.G.; Jiang, Y.Z.; Liu, Z.X.; Nerry, F. Land Surface Temperature and Emissivity Retrieval from Field-Measured Hyperspectral Thermal Infrared Data Using Wavelet Transform. Remote Sens. 2017, 9, 454. [Google Scholar] [CrossRef] [Green Version]
- Korb, A.R.; Dybwad, P.; Wadsworth, W.; Salisbury, J.W. Portable Fourier transform infrared spectroradiometer for field measurements of radiance and emissivity. Appl. Opt. 1996, 35, 1679–1692. [Google Scholar] [CrossRef] [Green Version]
- Salvaggio, C.; Miller, C.J. Methodologies and protocols for the collection of midwave and longwave infrared emissivity spectra using a portable field spectrometer. In Proceedings of the Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VII, Orlando, FL, USA, 16–19 April 2001; pp. 539–548. [Google Scholar]
- Christoph, H.; Simon, H.; Mark, V.D.M.; Wim, B.; Harald, V.D.W.; Henk, W.; Frank, V.R.; Boudewijn, D.S.; Freek, V.D.M. Thermal infrared spectrometer for Earth science remote sensing applications-instrument modifications and measurement procedures. Sensors 2011, 11, 10981–10999. [Google Scholar]
- Schlerf, M.; Rock, G.; Lagueux, P.; Ronellenfitsch, F.; Gerhards, M.; Hoffmann, L.; Udelhoven, T. A hyperspectral thermal infrared imaging instrument for natural resources applications. Remote Sens. 2012, 4, 3995–4009. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Xu, R.; Xie, F.; Jin, J.; Yuan, L.; Lv, G.; Wang, Y.; Li, C.; Wang, J. New Airborne Thermal-Infrared Hyperspectral Imager System: Initial Validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4149–4165. [Google Scholar] [CrossRef]
- Yousefi, B.; Sojasi, S.; Castanedo, C.I.; Beaudoin, G.; Huot, F.; Maldague, X.P.; Chamberland, M.; Lalonde, E. Emissivity retrieval from indoor hyperspectral imaging of mineral grains. In Proceedings of the Thermosense: Thermal Infrared Applications XXXVIII, Baltimore, MD, USA, 18–21 April 2016; p. 98611C. [Google Scholar]
- Balick, L.; Gillespie, A.; French, A.; Danilina, I.; Allard, J.-P.; Mushkin, A. Longwave thermal infrared spectral variability in individual rocks. IEEE Geosci. Remote Sens. Lett. 2008, 6, 52–56. [Google Scholar] [CrossRef]
- Farley, V.; Belzile, C.; Chamberland, M.; Legault, J.-F.; Schwantes, K.R. Development and testing of a hyperspectral imaging instrument for field spectroscopy. In Proceedings of the Imaging Spectrometry X, Denver, CO, USA, 2–4 August 2004; pp. 29–36. [Google Scholar]
- Ingram, P.M.; Muse, A.H. Sensitivity of iterative spectrally smooth temperature/emissivity separation to algorithmic assumptions and measurement noise. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2158–2167. [Google Scholar] [CrossRef]
- Shao, H.; Liu, C.; Li, C.; Wang, J.; Xie, F. Temperature and Emissivity Inversion Accuracy of Spectral Parameter Changes and Noise of Hyperspectral Thermal Infrared Imaging Spectrometers. Sensors 2020, 20, 2109. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Qian, Y.G.; Ma, L.L.; Tang, L.L.; Li, C.R. Influence of Sensor Spectral Properties on Temperature and Emissivity Separation for Hyperspectral Thermal Infrared Data. In Proceedings of the2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (Whispers), Los Angeles, CA, USA, 21–24 August 2016. [Google Scholar]
- Shao, H.L.; Liu, C.Y.; Xie, F.; Li, C.L.; Wang, J.Y. Noise-sensitivity Analysis and Improvement of Automatic Retrieval of Temperature and Emissivity Using Spectral Smoothness. Remote Sens. 2020, 12, 2295. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Gillespie, A.R. Surface Emissivity Retrieval From Airborne Hyperspectral Scanner Data: Insights on Atmospheric Correction and Noise Removal. IEEE Geosci. Remote Sens. Lett. 2012, 9, 180–184. [Google Scholar] [CrossRef]
- Borel, C.C. Surface emissivity and temperature retrieval for a hyperspectral sensor. In Proceedings of the IGARSS’98. Sensing and Managing the Environment. 1998 IEEE International Geoscience and Remote Sensing. Symposium Proceedings. (Cat. No. 98CH36174), Seattle, WA, USA, 6–10 July 1998; pp. 546–549. [Google Scholar]
- Hernandez-Baquero, E.D.S.; John, R. Atmospheric compensation for surface temperature and emissivity separation. In Proceedings of the Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VI, Orlando, FL, USA, 24–26 April 2000; pp. 400–410. [Google Scholar]
- Borel, C.C. ARTEMISS—An algorithm to retrieve temperature and emissivity from hyper-spectral thermal image data. In Proceedings of the 28th Annual GOMACTech Conference, Hyperspectral Imaging Session, Tampa, FL, USA, 31 March–3 April 2003; pp. 1–4. [Google Scholar]
- Wang, N.; Tang, B.H.; Li, C.R.; Li, Z.L. A Generalized Neural Network for Simultaneous Retrieval of Atmospheric Profiles and Surface Temperature from Hyperspectral Thermal Infrared Data. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1055–1058. [Google Scholar] [CrossRef]
- Wang, N.; Wu, H.; Nerry, F.; Li, C.; Li, Z.-L. Temperature and emissivity retrievals from hyperspectral thermal infrared data using linear spectral emissivity constraint. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1291–1303. [Google Scholar] [CrossRef]
- Wu, H.; Wang, N.; Ni, L.; Tang, B.-H.; Li, Z.-L. Practical retrieval of land surface emissivity spectra in 8–14 μm from hyperspectral thermal infrared data. Opt. Express 2012, 20, 24761–24768. [Google Scholar] [CrossRef]
- Adler-Golden, S.; Conforti, P.; Gagnon, M.; Tremblay, P.; Chamberland, M. Remote sensing of surface emissivity with the telops Hyper-Cam. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; pp. 1–4. [Google Scholar]
- Farley, V.; Vallières, A.; Chamberland, M.; Villemaire, A.; Legault, J.-F. Performance of the FIRST: A Long-Wave Infrared Hyperspectral Imaging Sensor; SPIE: Stockholm, Sweden, 2006; Volume 6398. [Google Scholar]
- Wang, M.; Zheng, S.; Li, X.; Qin, X. A new image denoising method based on Gaussian filter. In Proceedings of the 2014 International Conference on Information Science, Electronics and Electrical Engineering, Sapporo, Japan, 26–28 April 2014; pp. 163–167. [Google Scholar]
- Luo, J.; Ying, K.; Bai, J. Savitzky–Golay smoothing and differentiation filter for even number data. Signal Process. 2005, 85, 1429–1434. [Google Scholar] [CrossRef]
- Borel, C.C. Iterative retrieval of surface emissivity and temperature for a hyperspectral sensor. In Proceedings of the Proceedings for the First JPL Workshop on Remote Sensing of Land Surface Emissivity, Pasadena, CA, USA, 6–8 May 1997. [Google Scholar]
- Adler-Golden, S.M.; Conforti, P.; Gagnon, M.; Tremblay, P.; Chamberland, M. Long-wave infrared surface reflectance spectra retrieved from Telops Hyper-Cam imagery. In Proceedings of the SPIE Defense + Security, Baltimore, MD, USA, 6–7 May 2014; p. 8. [Google Scholar]















| Parameter | Value |
|---|---|
| Spectral resolution | |
| Spectral range | |
| Integration time | |
| Imaging size | 227 × 125 pixel |
| IFOV | 0.35 mrad |
| Cold blackbody temperature | 10 °C |
| Warm blackbody temperature | 30 °C |
| Quantitative value | 16 bit |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Cao, L.; Zhong, Y.; Jia, Z. Field-Based High-Quality Emissivity Spectra Measurement Using a Fourier Transform Thermal Infrared Hyperspectral Imager. Remote Sens. 2021, 13, 4453. https://doi.org/10.3390/rs13214453
Gao L, Cao L, Zhong Y, Jia Z. Field-Based High-Quality Emissivity Spectra Measurement Using a Fourier Transform Thermal Infrared Hyperspectral Imager. Remote Sensing. 2021; 13(21):4453. https://doi.org/10.3390/rs13214453
Chicago/Turabian StyleGao, Lyuzhou, Liqin Cao, Yanfei Zhong, and Zhaoyang Jia. 2021. "Field-Based High-Quality Emissivity Spectra Measurement Using a Fourier Transform Thermal Infrared Hyperspectral Imager" Remote Sensing 13, no. 21: 4453. https://doi.org/10.3390/rs13214453
APA StyleGao, L., Cao, L., Zhong, Y., & Jia, Z. (2021). Field-Based High-Quality Emissivity Spectra Measurement Using a Fourier Transform Thermal Infrared Hyperspectral Imager. Remote Sensing, 13(21), 4453. https://doi.org/10.3390/rs13214453